突破外形干擾建構(gòu)適用模型
——由一道考題的分析說起

☉江蘇省如皋市石莊鎮(zhèn)初級中學(xué) 孫來扣

突破外形干擾建構(gòu)適用模型
——由一道考題的分析說起

☉江蘇省如皋市石莊鎮(zhèn)初級中學(xué) 孫來扣

數(shù)學(xué)模型，生成于學(xué)生的數(shù)學(xué)認(rèn)知活動之中，是學(xué)生化解新的數(shù)學(xué)問題的重要工具.在初中階段，很多數(shù)學(xué)問題的解決都需要借助已有的數(shù)學(xué)模型，如相似問題中的“K形圖”、二次函數(shù)的幾種常用解析式等.這些數(shù)學(xué)模型是學(xué)生的數(shù)學(xué)認(rèn)知活動的規(guī)律總結(jié)，在一定范圍內(nèi)具有普遍性和適用性.因此，在教學(xué)中，一線老師對模型教學(xué)十分關(guān)注，他們努力將模型建構(gòu)在學(xué)生獲得“四基”的過程之中，讓學(xué)生不斷經(jīng)歷用已有數(shù)學(xué)模型解決新的數(shù)學(xué)問題的過程.然而，在模型應(yīng)用過程中，很多學(xué)生記住了數(shù)學(xué)模型的外表——“形”，而忽視了模型的內(nèi)核——“型”（即“內(nèi)在的知識結(jié)構(gòu)”），在很多新的問題的化解中選擇了一些看似適用卻不能用的模型，導(dǎo)致無法求解.近期的模擬考試中，就遇到了這樣一道題，其解答狀況令人擔(dān)憂.現(xiàn)結(jié)合這道試題的考情分析，談?wù)劰P者對模型教學(xué)的思考，希望對您有幫助.

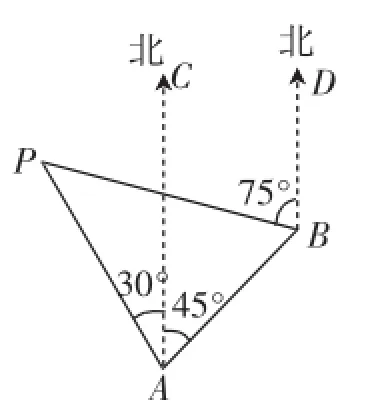
圖1

一、原題簡析

原題如圖1，一貨輪在A處，測得燈塔P在貨輪的北偏西30°的方向上，隨后貨輪以30海里/小時的速度沿北偏東45°的方向航行，40分鐘后到達(dá)B處，此時測得燈塔P在貨輪的北偏西75°的方向上.求此時貨輪距離燈塔P的距離PB（結(jié)果保留根號）.

簡析：這是一道銳角三角函數(shù)的應(yīng)用題，主要考查方位角、解直角三角形、銳角三角函數(shù)的定義、等腰三角形的性質(zhì)和勾股定理等知識.根據(jù)學(xué)生的現(xiàn)有認(rèn)識水平，原圖中的具有公共邊的兩個三角形在解答本題時并不適用，需要打破原來的三角形的分割方法，重新建構(gòu)“具有公共邊的兩個直角三角形”.因此，找出建構(gòu)有效的數(shù)學(xué)模型的有效途徑，是學(xué)生化解本題的關(guān)鍵.

正解：如圖2，過點A作AE⊥PB于點E.

根據(jù)“30海里/小時”和“40分鐘后到達(dá)”，可得AB= 20海里.

由AC∥BD，可得∠DBA=180°-∠CAB=135°.顯然，∠PBA=60°.

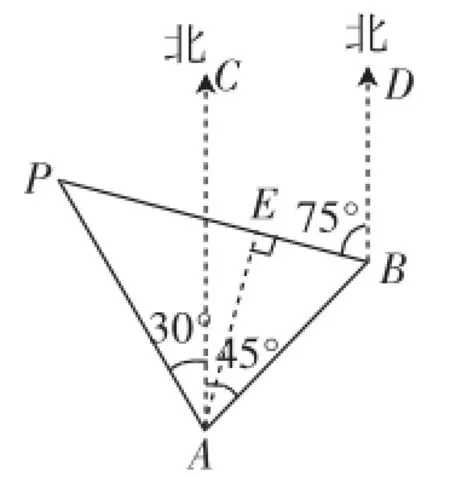
圖2

在Rt△APE中，∠EAP=∠EPA= 45°，根據(jù)“等腰三角形的性質(zhì)”，易得PE=AE=10海里.

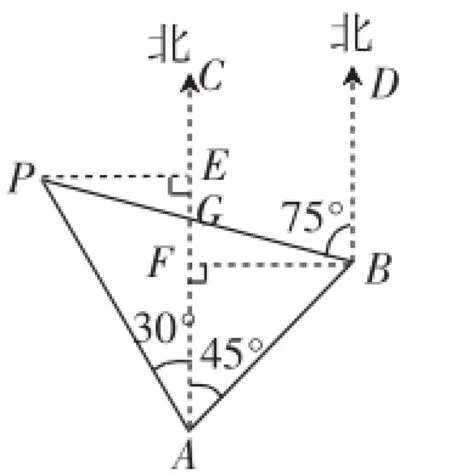
圖3

二、考情分析

考情簡述：在這次測試中，能完整給出“正解”過程的同學(xué)并不多.試卷批閱結(jié)束后，筆者對學(xué)生的解答狀況進(jìn)行了詳細(xì)分析，并與部分解答出錯的同學(xué)進(jìn)行了交流.通過分析與交流，發(fā)現(xiàn)絕大多數(shù)出錯的同學(xué)是“設(shè)AC與PB相交于點G”（如圖3），然后想利用圖中的△PAG和△BAG來解決問題.但由于這兩個三角形不是直角三角形，他們求解時發(fā)現(xiàn)銳角三角函數(shù)并不能發(fā)揮作用.于是，他們“分別作出了△PAG和△BAG的邊AG上的高PE和BF”，構(gòu)造出了一個含有30°和一個含有45°的直角三角形.看似熟悉的直角三角形，卻讓他們的求解陷入了“困境”，圍繞這樣兩個三角形做了很多“文章”，但最終都無功而返.顯然，圍繞原圖作出的這些分析并沒有給這道問題的解答“敞開大門”，反而讓接下來的求解之路越走越窄，最終得不到正確的答案也就無法避免了.

原因分析：在銳角三角函數(shù)的教學(xué)中，學(xué)生已經(jīng)建構(gòu)了一些解題模型.如圖4，這是“有一條公共邊的兩個疊合的直角三角形”模型；如圖5，這是“有一條公共邊的兩個疊合的直角三角形”模型.圖5中，AD為△ABC的邊BC上的高，恰好是Rt△ABD和Rt△ACD的公共邊，通過AD可以將兩個直角三角形關(guān)聯(lián)起來.上面的試題出現(xiàn)“大面積”無解，正是這一模型的“誤導(dǎo)”.出錯學(xué)生均誤認(rèn)為圖1中△PAB是圖5中的△ABC繞點A進(jìn)行的旋轉(zhuǎn)，AD恰好旋轉(zhuǎn)到了圖1中的豎直位置上的AC處.看似沒有關(guān)聯(lián)的圖形，經(jīng)過學(xué)生腦海中的一轉(zhuǎn)，配上了圖1中數(shù)據(jù)30°與45°被AC的“準(zhǔn)確”分割，學(xué)生不重新分割三角形，直接順著AC求解也就不足為奇了.

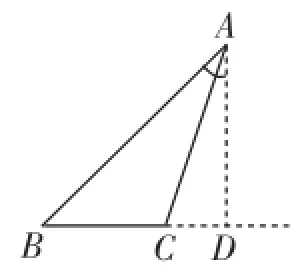
圖4

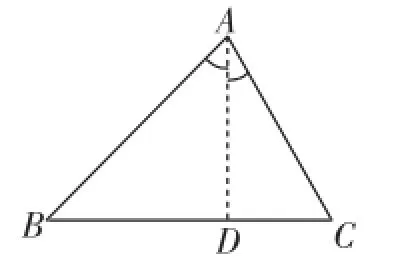
圖5

三、模型教學(xué)的幾點思考

從上面的分析我們不難發(fā)現(xiàn)，學(xué)生在應(yīng)用解題模型化解數(shù)學(xué)問題時，主要關(guān)注的還是“形”，只注重模型的外表，而忽略了模型的內(nèi)在知識關(guān)聯(lián)，讓模型的應(yīng)用僅停留在“臨摹”的層次上.要想學(xué)生在問題解決的過程中突破模型的外形迷惑，我們可以從以下幾個方面做些努力.

1.模型教學(xué)立足“四基”，強化關(guān)聯(lián)

“數(shù)學(xué)模型，運用符號或數(shù)學(xué)公式，予以模擬表示”，它生成于學(xué)生的數(shù)學(xué)認(rèn)知活動中，是學(xué)生經(jīng)歷探究活動歸納總結(jié)出的用以化解數(shù)學(xué)問題的工具，具有較強的延續(xù)性和適用性.在初中階段，數(shù)學(xué)模型比較簡單，綜合程度不高.很多數(shù)學(xué)模型是由一個或幾個數(shù)學(xué)知識整合而成，提取與應(yīng)用這些模型所涉及的知識與技能并不復(fù)雜，這些模型主要指向簡單的數(shù)學(xué)問題或?qū)嶋H問題.基于上述特點，在初中階段，我們應(yīng)將模型教學(xué)蘊含在學(xué)生獲得基礎(chǔ)知識、基本技能、基本數(shù)學(xué)思想及基本活動經(jīng)驗的過程之中，讓模型建構(gòu)在“四基”之上，以知識獲得為起點，以模型生成為中間目標(biāo)，以堅實的認(rèn)知基礎(chǔ)成就有效的數(shù)學(xué)模型.由于初中階段的數(shù)學(xué)模型是基礎(chǔ)模型，為了凸顯出數(shù)學(xué)模型在問題解決中的作用，我們應(yīng)將這些基礎(chǔ)模型進(jìn)行有效關(guān)聯(lián)，將關(guān)聯(lián)較大的數(shù)學(xué)模型鏈接成串，形成有效的“模型鏈”.在學(xué)生解決問題時，提取和應(yīng)用數(shù)學(xué)模型也就會出現(xiàn)“牽一發(fā)而動全身”的“鏈接效應(yīng)”.以垂徑定理為例，我們由圓的軸對稱性獲得了垂徑定理，產(chǎn)生了“垂徑定理直角三角形”，此時可以鏈接上“勾股定理”模型，在勾股定理模型之上，再鏈接上方程模型，這樣就形成了一個以“勾股定理”模型為橋梁的“模型鏈”.提取這一模型解題，學(xué)生自然會思前想后，在模型的選擇和應(yīng)用上敞開思路，得到正解.再以上面的試題為例，圖4是“有公共邊的兩個直角三角形”模型，我們可以將其與勾股定理、方程、常用三角函數(shù)關(guān)聯(lián)，形成一個“模型鏈”.這樣一來，化解此題自然就有多條路徑了，自然就不會出現(xiàn)“只讀圖形，而忽略了文字、符號之間的聯(lián)系”的情形了.顯見，數(shù)學(xué)模型鏈的生成，能讓學(xué)生從多個角度思考數(shù)學(xué)問題，能幫助學(xué)生有效突破一些外在表象的迷惑，為學(xué)生獲得有效的解題途徑提供了多種可能.

2.模型建構(gòu)反復(fù)嘗試，力求適用

反復(fù)嘗試，是數(shù)學(xué)模型建構(gòu)的必經(jīng)之路.任何數(shù)學(xué)問題或生活問題的解決，都不是一蹴而就的.理清問題的情境需要反復(fù)嘗試，一字、一詞、一句、一符、一圖都需要學(xué)生反復(fù)揣摩，方能捕捉到有用的問題解決的信息；明晰問題的指向和解題所需知識的需求反復(fù)嘗試，問題解決必須先摸清問題的來路，當(dāng)我們能順著問題的“來路”繼續(xù)走下去，才會讓解題變得順暢；分析解題思路和解題方法需要反復(fù)嘗試，走得通，再走走，走不通，回頭再來，實在不行，換個角度再看看，問題解決本應(yīng)如此；形成解題模型還是要反復(fù)嘗試，初中階段的數(shù)學(xué)問題和實際問題有一定的綜合性，還是需要模型組合的，加之?dāng)?shù)學(xué)模型隱藏在學(xué)生的認(rèn)知網(wǎng)絡(luò)中，并不會隨時隨地出現(xiàn)，因此，必要的反復(fù)嘗試將會讓學(xué)生找到最佳的解題模型，讓他們在適用的基礎(chǔ)上“定下心來，就這么做了”.圖3是學(xué)生選擇的適用于解決“原題”的有效模型，然而思維定勢讓他們沒能繼續(xù)沿著這一模型走下去，造成這一結(jié)果的原因是多方面的.對原圖的盲從，讓他們的思維始終定格在模型的“外形”上，從問題分析開始，“熟悉感”讓他們走上了一條“無法求解”的道路；在問題解決時，反復(fù)在同一條路上嘗試，讓他們心生煩躁，懊惱自不必說，甚至開始懷疑老師與自己共同努力建構(gòu)的數(shù)學(xué)模型有“問題”.應(yīng)該說，學(xué)生產(chǎn)生這樣的想法并不意外，在測試后就有學(xué)生表達(dá)了自己的想法，筆者通過一個手勢進(jìn)行了指點，學(xué)生立即明白了，并大為感嘆：我怎么沒敢這么想呢？早知道我也試一下了.看來，還是嘗試的力度不夠，在教學(xué)中，應(yīng)鼓勵學(xué)生反復(fù)嘗試，只有不斷試誤，才能發(fā)現(xiàn)問題解決的最佳路徑，才能獲得最適用的問題解決的數(shù)學(xué)模型.

3.模型應(yīng)用關(guān)注本質(zhì)，及時抽象

對初中階段的學(xué)生來說，能夠想到用數(shù)學(xué)模型去解決新的數(shù)學(xué)問題，是一件不簡單的事情.當(dāng)學(xué)生出現(xiàn)這樣的解題行為時，我們應(yīng)予以鼓勵并加以引導(dǎo)，讓他們經(jīng)歷“抽象問題情境，建構(gòu)解題模型”的過程，讓他們充分感知數(shù)學(xué)模型與“四基”間的聯(lián)系，學(xué)會從本質(zhì)上應(yīng)用模型.細(xì)細(xì)分析試題的解答狀況，慢慢解讀學(xué)生的求解歷程，一個問題自然而然就呈現(xiàn)在眼前：為什么想不到圖2中的輔助線AE呢？“設(shè)AC與PB相交于點G”看似應(yīng)用了圖3這一模型，實則是沒能理清圖3的真正內(nèi)涵，關(guān)注外在的“形”，而忽略了內(nèi)在的“神”.圖3是“有公共邊的兩個直角三角形”模型，公共邊是模型的一個條件，兩個三角形也是一個重要條件，這些都是學(xué)生的關(guān)注點，出錯的學(xué)生對此關(guān)注尤為到位.要注意的是，這個模型中的一個更為重要的條件是“直角三角形”，如果將這個條件忽略了，接下來的求解自然就會缺少“直角三角形”的支撐.在現(xiàn)階段，直接利用圖1求三角形中的邊和線，顯然是十分困難的.所以很多學(xué)生無法給出正確的解題過程也就在意料之中了.這就告訴我們，在今后解決數(shù)學(xué)問題或?qū)嶋H問題時，應(yīng)關(guān)注問題與數(shù)學(xué)模型的本質(zhì)之間的內(nèi)在關(guān)聯(lián)，將問題情境中的條件與數(shù)學(xué)模型的核心條件認(rèn)真比對，確保從問題情境中抽象出的解題模型與已有的數(shù)學(xué)模型高度相似.當(dāng)兩者之間有明顯差別時，我們應(yīng)對解題模型進(jìn)行必要的調(diào)整，一方面，再回問題情境重建解題模型，直到完全匹配才能結(jié)束探究.另外，我們也可以適度修正解題模型，通過添加輔助條件等方式實現(xiàn)模型間的匹配.總之，解題模型的建構(gòu)應(yīng)以適用為終極目標(biāo).

四、結(jié)束語

數(shù)學(xué)模型與學(xué)生的數(shù)學(xué)探究活動息息相關(guān)，它們在新知探究過程中生成，在解題訓(xùn)練中得到鞏固與提升.在問題解決過程中，能不能建構(gòu)出有效的數(shù)學(xué)模型非常重要.毋庸置疑，模型“外形”特征對學(xué)生提取與應(yīng)用合適的模型解題干擾很大.為此，新知教學(xué)中，我們應(yīng)為模型建構(gòu)準(zhǔn)備充足條件，儲備模型生成必需的基礎(chǔ)知識和基本技能；復(fù)習(xí)鞏固時，應(yīng)突出模型間的關(guān)聯(lián)與融合，形成有效的模型鏈，讓模型應(yīng)用“牽一發(fā)而動全身”；解題訓(xùn)練時，我們設(shè)置不同變式模型應(yīng)用訓(xùn)練，不斷強化學(xué)生對核心模型的應(yīng)用體驗……總之，數(shù)學(xué)模型的應(yīng)用不應(yīng)為外形所干擾.能想到用模型解題是一種進(jìn)步，能選擇適用的數(shù)學(xué)模型說明學(xué)生的數(shù)學(xué)思維又向前邁出了一步，而真正說明學(xué)生數(shù)學(xué)思維卓有成效的是用適用的模型化解新的數(shù)學(xué)問題.在這條路上，我們還要做很多事，比如找到模型教學(xué)的最佳時點，找到不同模型之間的銜接點等.期待您能參與到模型教學(xué)的研究中來，同時，也懇請您能對本文中的不足提出寶貴的意見和建議.

1.中華人民共和國教育部制定.義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）［M］.北京：北京師范大學(xué)出版社，2012.

2.高俊元.一組旨在改變學(xué)生學(xué)習(xí)方式的中考題［J］.中學(xué)數(shù)學(xué)雜志（初中版），2006（1）.

3.丁銀杰.“銳角三角函數(shù)”課本習(xí)題拓展探究［J］.初中生世界（九年級），2014（2）.

4.印冬建.突出核心主線追求有效教學(xué)——談初中數(shù)學(xué)有效備課的做法與思考［J］.中學(xué)數(shù)學(xué)（下），2014（1）.