科氏質量流量計靈敏度溫度補償方法研究

0 引言

科氏質量流量傳感器（Coriolis Mass Flowmeter，簡稱CMF）是一種直接敏感被測流體質量流量的高性能諧振式傳感器。其具有重復性高、精度高、穩定性好等優點，并且其內部結構簡單，無可動部件，因而其可靠性好，使用壽命長，還能測量高壓氣體和高粘度流體的流量。科氏質量流量計越來越廣泛的應用在石油、化工、建材、造紙、醫藥、食品、生物工程、冶金、能源、航天等工業部門，是貿易交接和過程控制的重要的高精度、多參數測量儀表[1-3]。

隨著CMF的廣泛使用，其在不同工況情況下的精度問題也越來越得到用戶的重視，其中溫度影響是用戶普遍關注的重要影響因素之一。從諧振的理論角度，材料的彈性模量會隨著材料溫度的變化變化，為此，科氏質量流量計在測量管的入口端均會設置溫度傳感器，實時測量測量管溫度的變化，進而對流量計進行溫度補償，且測量管的結構不同，則溫度影響也不盡相同。

美國MICROMOTION、德國E+H等產品在溫度補償方面比較完善，在產品樣本中均對溫度補償后的精度進行了描述。以MICROMOTION公司ELITE產品為例，CMF400型流量計，其溫度變化對精度的影響為：±0.0007%×最大流量值/℃。國內生產質量流量計的廠家主要包括：西安東風機電、太航流量儀表、北京首科實華、上海一諾等公司，從各公司產品的樣本中，看到均有溫度補償的描述性語言，但溫度對精度變化影響的描述缺少定量數據[4-8]。

為此，本文結合公司門型管CMF產品，從理論分析和實驗測試方面建立和完善了流量計的溫度補償模型，提升了公司產品的溫度適應性。

1 質量流量計理論模型

1.1 科里奧利效應

科里奧利效應(科氏效應)是由法國實驗物理學家科里奧利(G.G.Coriolis)于1835年首先提出的。科氏加速度是旋轉坐標系中物體的相對直線運動而產生的加速度，方向垂直于旋轉坐標系的角速度矢量和物體的相對速度矢量，如圖1所示，表述為

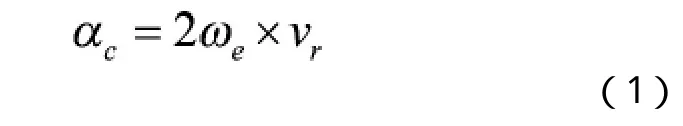
式(1)中，ωe為旋轉坐標系相對于靜參考系的角速度；vr為物體相對于旋轉坐標系的速度；αc為科氏加速度，方向垂直于角速度矢量和相對速度矢量。質量為m的質點，由科氏加速度形成的慣性力為科氏力。

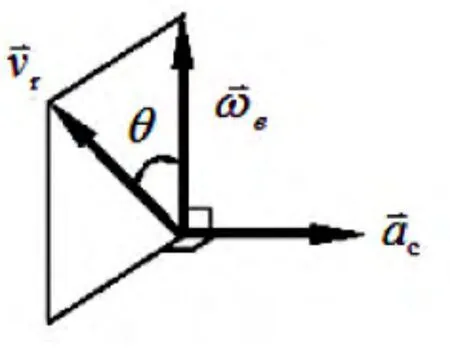
圖1 科氏加速度矢量關系示意圖Fig.1 The coriolis acceleration vector relationship diagram

1.2 門型管質量流量計模型

圖2給出了門形管科氏質量流量傳感器的模型示意圖。當管中無流體流動時，諧振子在激勵單元的激勵下，產生繞CC'軸的彎曲主振動，可寫為[9,10]

式(2)中,為系統的主振動頻率，由包括彈性彎管在內的諧振子整體結構決定；對應的主振型；為沿管子軸線方向的曲線坐標。

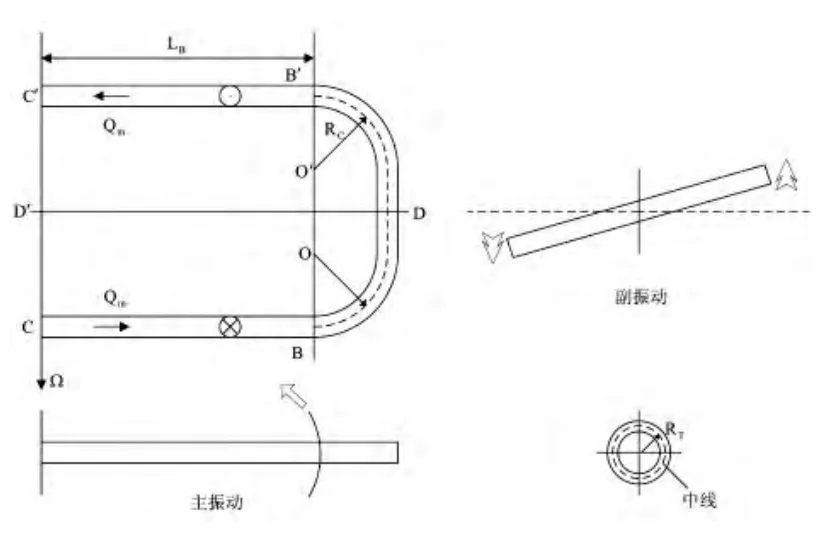
圖2 門形管科氏質量流量傳感器的模型示意圖Fig.2 Tube coriolis mass flow sensor model

測量管繞CC'軸周期性轉動的等效角速度為

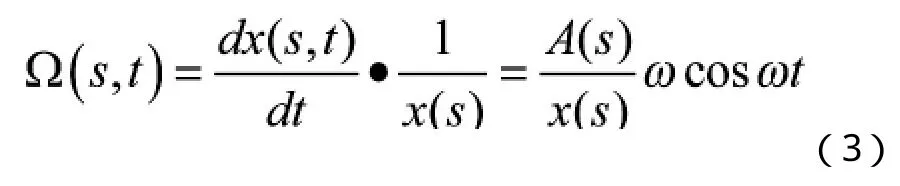
式(3)中,為管子上任一點到CC'軸的距離。

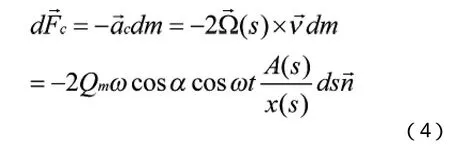
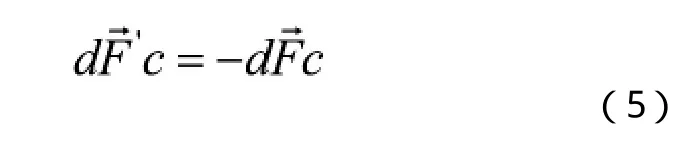
式(4)和式(5)相差一個負號，表示兩者方向相反。當有流體流過振動的諧振子時，在的作用下，將產生對軸的力偶

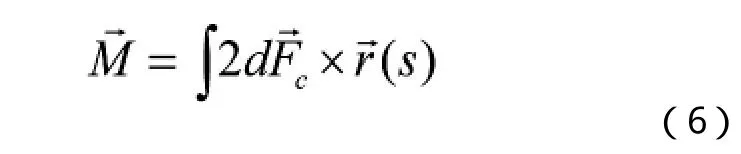
由式 (4)、(5)和 (6)得

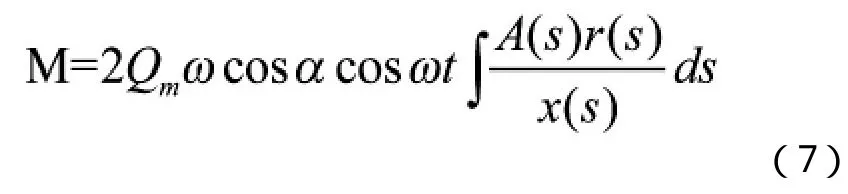
科氏效應引起的力偶將使諧振子產生一個繞軸的扭轉運動，相對于諧振子的主振動而言，稱為“副振動”，其運動方程可寫為[10,11]

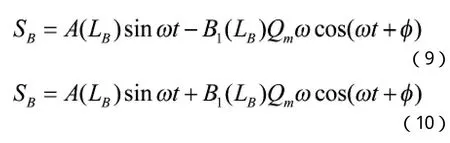
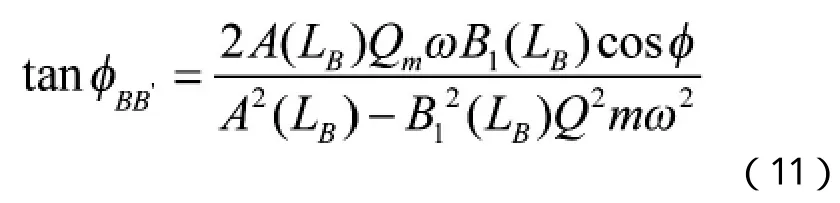
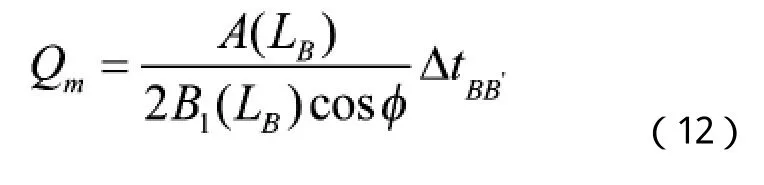
2 質量流量計溫度補償模型

2.1 材料溫度效應

科氏質量流量計在做理論分析時，為了便于分析，通常簡化甚至忽略了一些條件，得到的結論往往不受環境因素如溫度、密度、壓力、流體粘度等的影響。實際性能是受環境變化而變化的，其中溫度的影響最為突出，在實際高精度的應用場合中，科氏質量流量計要提高測量精度，必須考慮溫度效應[12,13]。

根據科氏質量流量計的組成與安裝形式，可以把溫度對流量計的影響分成兩部分：使用環境的溫度影響和介質工藝的溫度影響。使用環境的溫度影響是指環境溫度變化導致的轉換電路的溫度漂移。由于大部分變送器采用的是模擬數字混合處理的形式，而電路中的模擬器件包括電阻、電感、運放、比較器、電源和轉換器等都存在溫度漂移，因此使用環境溫度的變化會影響變送器信號模擬輸出電路。這種影響可從優化模擬處理電路的設計和選用溫度系數小的電子元器件兩方面來解決。介質工藝溫度的影響是指管內介質溫度的變化對傳感器的影響。該影響分兩方面：

1）流量零點溫度效應：是指介質溫度變化引起的敏感管幾何結構的不均衡變化，這種變化沒有規律，無法實施補償。

2）傳感器流量斜率溫度效應：是指溫度變化引起敏感管材料彈性模量的變化，這種變化是固定的，可以通過測試求出補償系數，實施補償。本文研究的就是傳感器的流量斜率溫度效應，擬通過解析法建立溫度補償模型，改善科氏質量流量計的測試性能。

綜上，研究溫度對質量流量計靈敏度的影響需要研究溫度對測量管材料的彈性模量的影響。科氏質量流量計的敏感管管材是不銹鋼，一般采用316L。大量實驗數據表明，不銹鋼的彈性模量隨溫度升高而降低[14-17]。彈性模量——溫度模型為

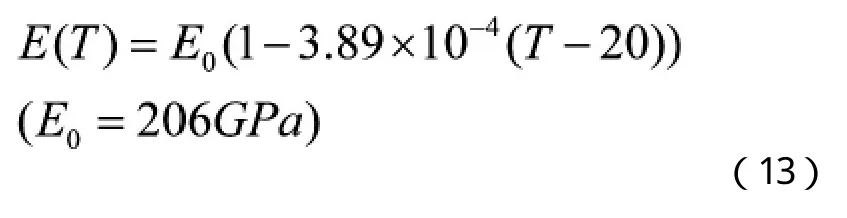
2.2 流量計溫度補償模型

結合本公司某型號產品的結構參數：測量管為直徑12mm×1mm，有效總長度為679.5mm，雙管結構，316L不銹鋼。

傳感器測量管的泊松比和彈性模量只與測量管的管材有關，因質量流量計采用316L管材，因此材料屬性部分常給定為默認值，泊松比u=0.3，彈性模量E=206GPa。

依據公式(12)，理論上該型號流量計的最大靈敏度隨溫度變化的曲線關系如圖3所示。

由二次擬合得到的溫度補償模型為其中K0=80.5532, a=5.3194E-18, b= -0.000389, c=1。

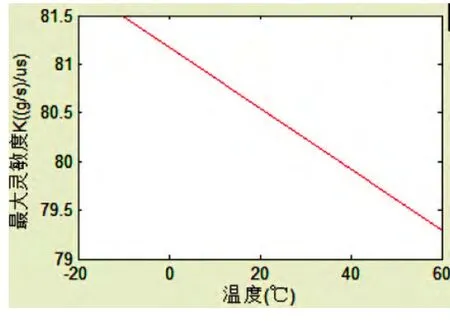
圖3 最大靈敏度隨溫度變化曲線Fig.3 Maximum sensitivity changes w ith temperature curves

3 實驗研究

為驗證流量計的溫度補償模型，在現有的靜態稱重法標定系統基礎上，增加了加溫控制系統，控制流體的溫度變化。系統目前能夠實現快速升溫和自然降溫冷卻。利用理論分析建模的傳感器進行標定和溫度實驗，實驗結果如表1所示。

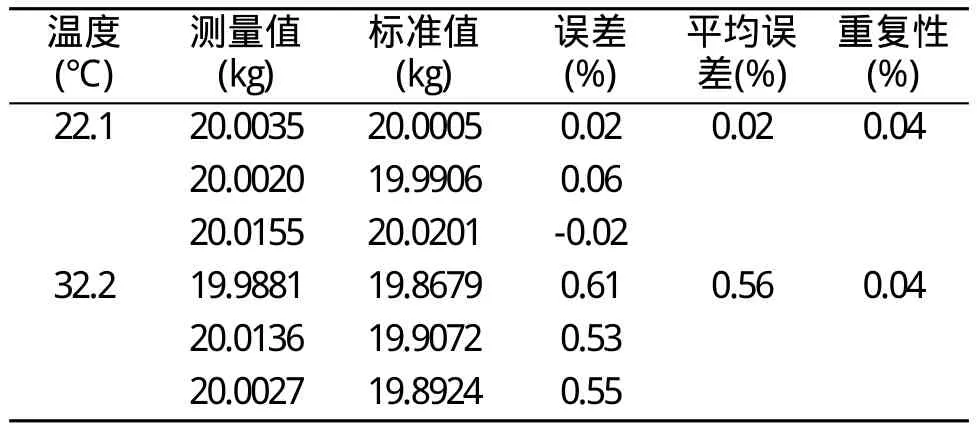
表1 靜態稱重法水溫變化標定實驗結果Table 1 Static weighing method for temperature calibration results

由表1可知，流量計的重復性可達0.05%，重復性良好。當溫度由22.1℃升高至32.2℃時，測量的相對誤差由+0.02%變化至+0.56%，變化了+0.54%，即溫度升高，誤差增大，溫度升高1℃，相對誤差增加+0.05347%/℃，為正偏差。

根據公式(14)，溫度補償模型擬合成二次曲線時其二次項數量級較低，對補償結果影響很小，本文進行了忽略，實際補償時直接用一次線性模型對流量計進行補償，即實際補償所用的模型為：

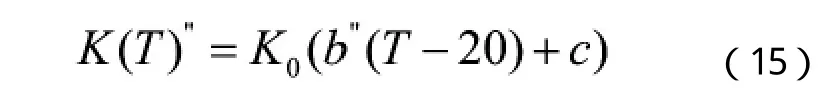
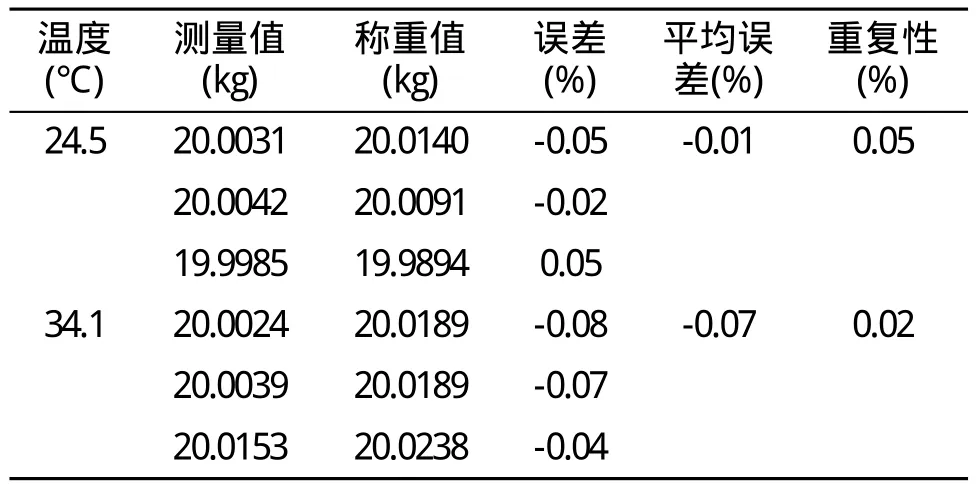
表2 流量計溫度補償后的標定結果Table 2 Flowmeter w ith temperature compensation calibration the results

由表2中可以看出，經過模型補償后，誤差減小，溫度升高1℃，相對誤差為-0.00625%/℃。

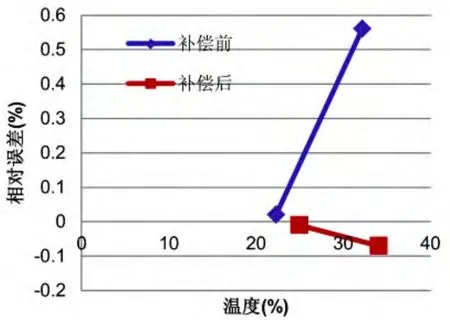
圖4 施加溫度補償前后測量的相對誤差Fig.4 Temperature compensation imposed before and after the relative error of measurement

如圖4所示，補償前流量計最大靈敏度的誤差為隨溫度變化較明顯，補償后變化趨勢趨于平緩。補償前相對誤差隨溫度變化為+0.05347%/℃，補償后為-0.00625%/℃，補償效果明顯。

理論分析得到的溫度補償模型與實驗所得模型相比，總體趨勢相同，都是靈敏度隨溫度升高而變大(可簡化視作線性關系)，但理論與實驗有一定誤差，產生誤差的原因有：科氏質量流量計實際生產加工的尺寸、材料方面的誤差等。

4 結束語

本文從科氏質量流量計的敏感機理出發，建立了流量計的靈敏度模型，并依據材料的彈性模量隨溫度變化的模型，建立了流量計的靈敏度和溫度的補償模型。改造了現有的靜態稱重法質量流量計標定裝置，對建模的流量計進行精度與流體溫度的實驗研究。理論與實驗結果表明：科氏質量流量計隨著流體溫度的升高，將產生正向的測量誤差，誤差與溫度的關系為二次曲線關系，在特定的溫度范圍內，可以簡化為直線關系；利用論文研究的溫度補償模型，流量計從未補償時的溫度與精度關系+0.05347%/℃降低為補償后的-0.00625%/℃，補償效果顯著。

[1]紀愛敏, 李川奇, 沈連官, 等.科里奧利質量流量計研究現狀及發展趨勢(一)[J].儀表技術與傳感器, 2001, 5(06): 1-3.

[2]R.S.Medlock, R.A.Furness.Mass flow measurement-a state of the art review[J].Measurement and Control, 1990, 23(5): 100-113.

[3]M.Shanmugavalli, M.Umapathy, G.Uma.Smart Coriolis mass flowmeter[J].Measurement, 2010, 43(4): 549-555.

[4]M icromotion, elite產品樣本,PS-00614, Rev.T,2012.7.

[5]西安東風機電有限公司, C系列選型(2012版), 2012.

[6]太原太航流量工程有限公司,選型手冊.

[7]北京首科實華自動化設備有限公司,選型手冊.

[8]上海一諾儀表有限公司,選型手冊.

[9]樊尚春.傳感器技術及應用[M].北京: 北京航空航天大學出版社, 2004: 308-332.

[10]紀愛敏.科里奧利質量流量計的建模研究與仿真分析[D].合肥: 中國科學技術大學, 2001.6.

[11]Drahm, W., Bjonnes, H.A Coriolis mass flowmeter with direct viscosity measurement[J].Com puting & Contro l Engineering Journal, 2003, 14(4): 42-43.

[12]孫玉聲, 姚小兵, 陳世超.科氏力質量流量計質量流量參量的溫度系數[J].中國測試技術, 2004, 30(3): 6-8.

[13]Martin Anklin, et al.Coriolis mass flow meters: Overview of the cu rrent state of the art and latest research [J].Flow Measurement and Instrumentation, 2006, 17(6): 317-323.

[14]Kazahaya, M.A Mathematical Model and Error Analysis of Coriolis Mass Flowmeters[J].Instrumentation and Measurement, 2011,60(4): 1163-1174.

[15]Tao Wang.Coriolis mass flowmeas urem en t at cryogenict em peratu res[J].Flow Measu rem en t and Instrumentation, 2009, 20: 110-115.

[16]陳駒, 金偉良, 楊立偉.建筑用不銹鋼的抗火性能[J].浙江大學學報(工學版), 2008, 42(11):1983-1989.

[17]王斌.核電用304/316奧氏體不銹鋼寬厚板加熱和熱軋過程的數值模擬[D].沈陽:東北大學, 2011.