復合材料機匣的彈性穩定性及振動特性研究

溫登哲，陳予恕，侯磊，李忠剛

(1.哈爾濱工業大學航天學院，哈爾濱150001;2.哈爾濱工業大學機械工程學院，哈爾濱150001)

復合材料機匣的彈性穩定性及振動特性研究

溫登哲1，陳予恕1，侯磊1，李忠剛2

(1.哈爾濱工業大學航天學院，哈爾濱150001;2.哈爾濱工業大學機械工程學院，哈爾濱150001)

采用Flügge殼體理論，分析了徑向內壓對復合材料機匣的彈性穩定性(屈曲特性)的影響，并討論了幾何參數及材料特性對屈曲特性的影響。研究分析表明，在強度允許的范圍內，徑向內壓的提高有助于提高機匣的抗屈曲能力。進一步應用振型疊加方法，研究了復合材料機匣在徑向內壓作用下受到徑向簡諧激勵作用時穩態動力響應問題，在特定徑向簡諧激勵的作用下，徑向位移響應的最大值在激勵面和非激勵面對應的頻率點不同，激勵面內出現在第三階頻率點處，而在非激勵面內則出現在基頻處。

復合材料機匣;圓柱殼;彈性穩定性;振型疊加法

航空發動機機匣整體結構近薄壁圓柱殼，受軸向力、內壓及徑向沖擊等多種載荷共同作用，容易發生屈曲，機匣的屈曲將破壞發動機進氣道，并使發動機產生劇烈振動甚至碰摩，嚴重時會使整個飛機發生抖動以及結構屈曲破壞［1］。先進復合材料由于其重量輕、剛度大、可設計性好、抗疲勞性能強等許多優異特性［2］，在航空發動機機匣上獲得了廣泛的應用，復合材料的應用，不僅減輕了發動機的重量，提高了推重比，而且提高了機匣的抗屈曲能力和運動穩定性。

從最近的研究成果來看，國內外對殼體結構的彈性穩定性研究主要集中在圓柱殼及加筋圓柱殼的屈曲方面［3－6］。仲政等［7］綜述了復合材料與結構的若干力學問題的最新研究進展，包括復合材料梁、板、殼結構的解析解和數值解，文中還提出了梯度有限元法、非傳統Hamilton原理、細觀元法等常用的數值方法。

Jones［8］研究了正交反對稱層合圓柱殼前屈曲變形對軸壓和側壓屈曲臨界載荷的影響，但研究工作局限于兩端簡支的邊界條件，結論不具有普遍性。唐文勇等［9］采用半解析法研究了徑向階躍載荷作用下復合材料圓柱殼的非線性動力屈曲問題，用有限差分法對方程進行了求解，通過B－R準則判定殼體是否發生屈曲，并確定了屈曲臨界載荷。齊紅宇等［10－11］利用線性板殼理論，對航空發動機樹脂基復合材料外涵道機匣進行了有限元建模，分析了機匣在軸向和徑向載荷單獨作用和耦合作用下的屈曲特性，研究發現，在軸向載荷和徑向載荷單獨作用和耦合作用下，復合材料機匣的屈曲部位均發生在機匣的內外表面。李健等［12］采用Runge－Kutta法和多尺度法對軸向運動的復合材料薄壁圓柱殼的非線性振動特性進行了理論研究，得到了系統由于固有頻率接近導致的內共振現象。翟葉高等［13］提出了一種半解析區域分解法來分析任意邊界條件的復合材料層合殼的振動，并將計算結果與其他文獻進行了對比，結果表明，該方法具有高效率、高精度和收斂性好等優點。陳強等［14］以纖維增強復合材料層合殼結構為研究對象，分析了邊界條件、鋪層數目和殼體幾何參數對殼體結構振動特性的影響。李戎等［15］以Flügge殼體理論為基礎，利用波動法推導了復合材料圓柱殼耦合系統的振動方程，并與各向同性殼材料圓柱殼的固有頻率進行了對比;材料參數，殼體厚度，長徑比及邊界條件等因素對復合材料圓柱殼的固有頻率影響巨大。

以上文獻從理論和數值方面對復合材料機匣及圓柱殼結構的彈性穩定性和振動特性進行了研究，但對于軸向力和徑向力耦合作用下的殼體屈曲和振動問題研究的還比較少，而在實際工況中，機匣是受到軸向力與徑向力耦合作用的影響，因此研究機匣在軸向力和徑向力耦合作用下的彈性穩定性及振動特性對實際工程設計有重要的意義。本文以受軸向力作用的復合材料機匣為研究對象，根據其幾何特征將其簡化為薄壁圓柱殼結構，考慮徑向力(徑向內壓和徑向簡諧激勵)對機匣的彈性穩定性及振動特性的影響，結果表明，徑向力及材料參數對機匣的彈性穩定性和振動特性影響巨大。

1 機匣的動力學方程

本文根據航空發動機機匣薄壁、整體呈柱狀的幾何特征，將機匣簡化為薄壁圓柱殼結構(見圖1)，圓柱殼長度為L，內半徑為R，厚度為h。坐標系oxyz，u，v，w分別為各坐標軸方向的位移;Q為均布徑向內壓，L0處截面作用徑向簡諧激勵p(t)f1(x0)，圖2為L0處機匣截面徑向簡諧激勵p(t)f1(x0)的示意圖。

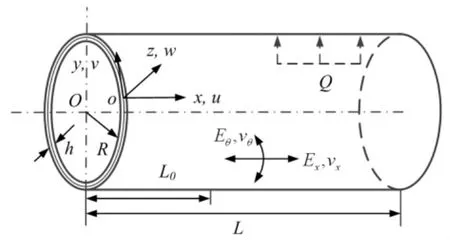
圖1 復合材料機匣示意圖Fig.1 Model of a composite case

假定復合材料的彈性主方向與機匣中面坐標oxyz方向一致，軸向彈性模量和泊松比分別為Ex，vx，周向的彈性模量和泊松比分別為Ex，vx且滿足關系。vxEθ=vθEx(1)

圖2 L0處徑向簡諧激勵示意圖Fig.2 Diagram of radial harmonic excitation on L0

機匣受軸向力和徑向力共同作用，其中徑向力包括徑向壓力Q和徑向簡諧激勵p(t)f1(x0)，根據Flügge殼體理論建立復合材料機匣的振動方程［16］

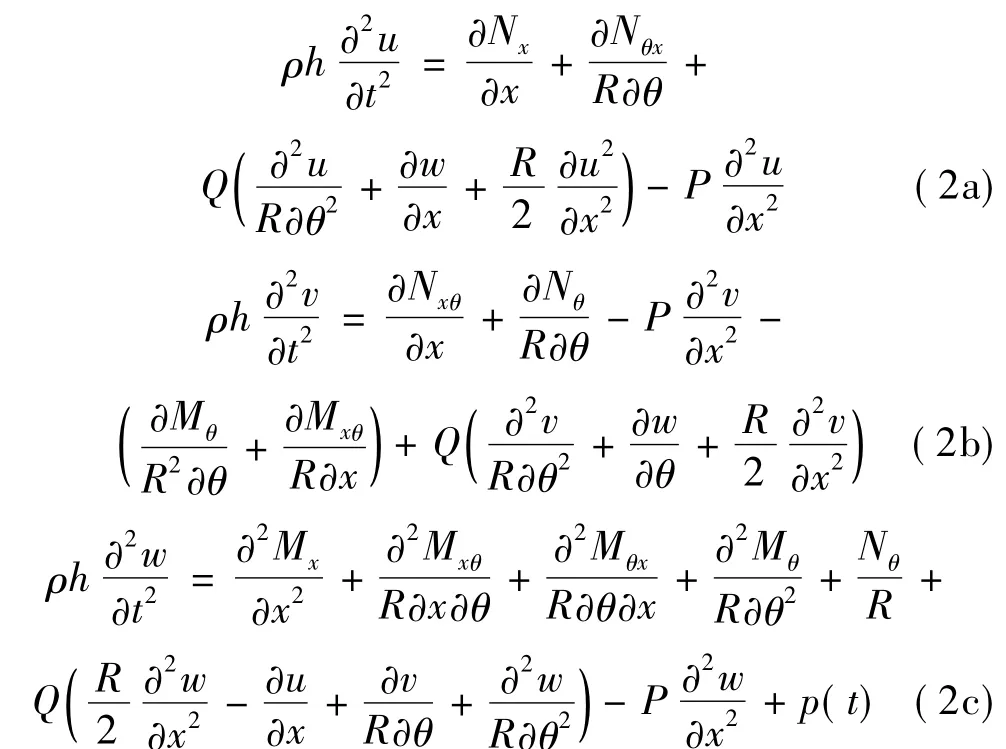
式中:P為軸向力，Q為徑向內壓，p(t)f1(x0)為徑向簡諧激勵，ρ為材料密度u，v，w分別為軸向、周向和徑向的位移。對于復合材料機匣，假定材料是勻質的，薄膜內力Nx，Nθ，Nxθ，Nθx，彎曲內力Mx，Mθ，Mxθ，Mθx與位移的關系表達式為:

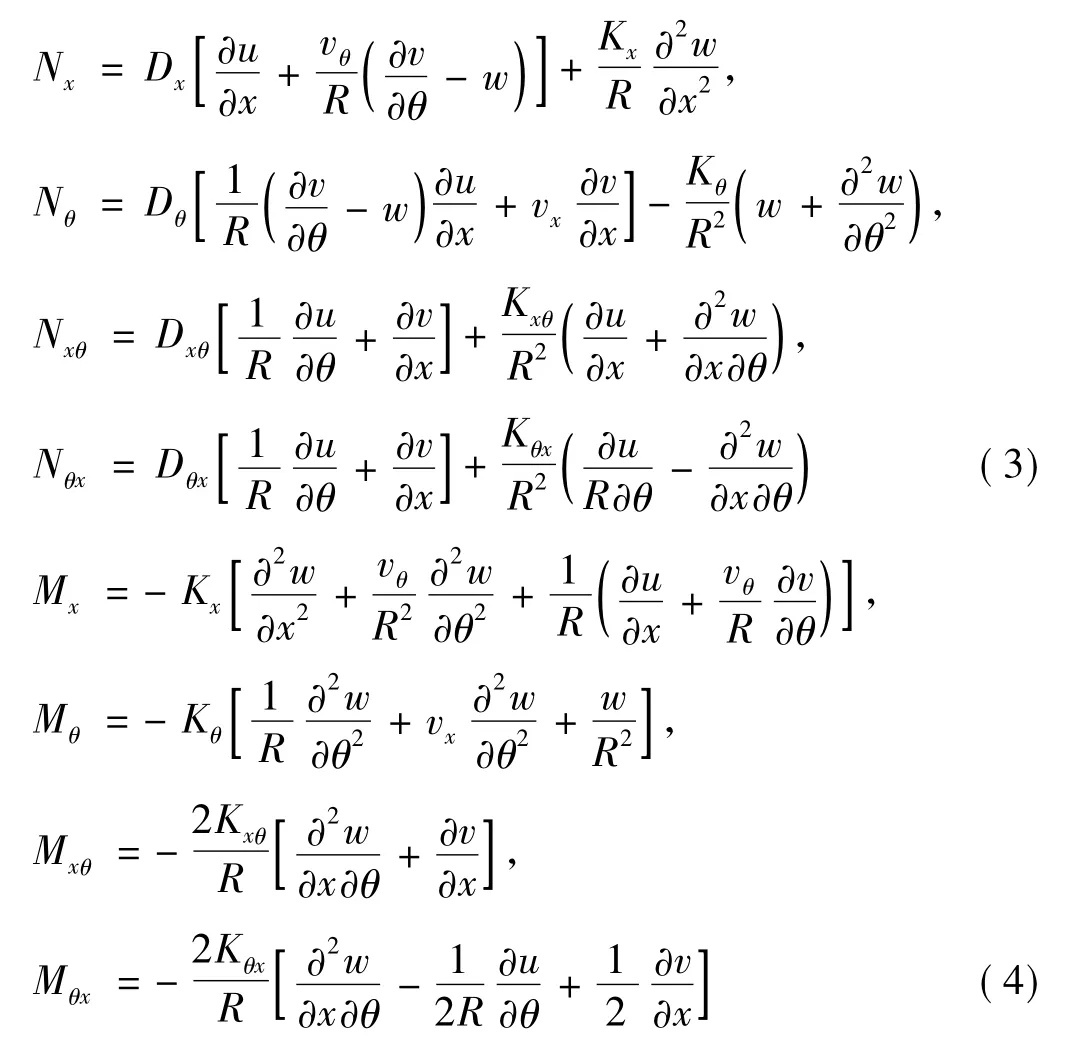
其中:

式中:Dx，Dθ，Dxθ為拉伸剛度，Kx，Kθ，Kxθ為彎曲剛度。

為了討論機匣幾何參數及材料參數對軸向失穩壓力Pcr的影響，本文討論了5種典型的材料［17］。

表1 5種典型材料的參數Tab.1 Parameters of five typicalmaterials

2 機匣的彈性穩定性分析

2.1 軸向失穩壓力的計算

本節分析機匣在徑向內壓作用下的軸向失穩壓力問題，令徑向簡諧激勵為零:

將式(3)，式(4)，式(5)，式(6)代入式(2)中，式(2)可寫為矩陣的形式

式中Lij(i，j=1，2，3)是微分算子，表達式為:

設位移函數表達式為:

式中λ=mπ/L，m表示軸向半波數，n表示周向波數。

將式(9)代入式(7)，得:

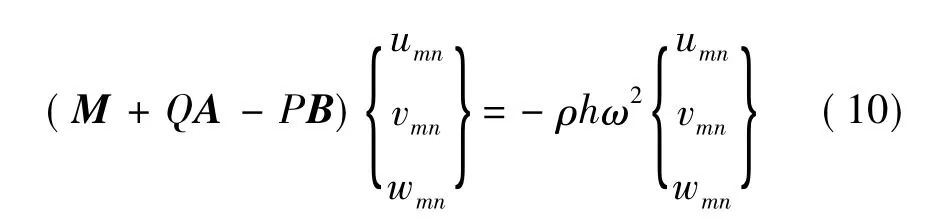
其中P，Q分別為軸向壓力和徑向內力，矩陣M，A，B的表達式為:

研究系統在軸向力作用下徑向內壓Q對軸向失穩壓力Pcr的影響，式(10)為機匣在軸向力P和徑向內壓Q共同作用下振動的特征方程，令式(10)的右端為{0，0，0}T，系數行列式等于零為機匣失穩的臨界條件表達為:

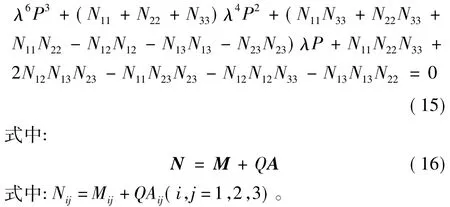
2.2 機匣彈性穩定性分析

根據上述理論推導，本節對復合材料機匣的彈性穩定性問題進行數值計算。定義軸向臨界失穩壓力Pcr:

圖3為兩種不同長度圓柱殼的軸向失穩壓力和失穩波形的關系，圖3(a)和圖3(c)對應的失穩波形分別為m=1，n=4和m=1，n=2;對比圖3(a)和圖3(c)可知，長徑比對軸向失穩壓力有較大影響，且長圓殼的失穩壓力較短殼的失穩壓力小。圖3(b)和圖3(d)為存在徑向內壓時兩不同長度圓柱殼的軸向失穩壓力與失穩波形的關系，分別對比圖3(a)和圖3(b)、圖3(c)和圖3(d)可知，徑向內壓的存在，不僅增大了失穩壓力，而且對失穩壓力對應的失穩波形也有所影響。

圖4為徑向內壓和材料參數對軸向失穩壓力和周向波數的影響，圖4(a)可知，材料3～材料5，近似認為Ex不變化，周向彈性模量Eθ的逐漸增大，Eθ的增大有效的提高了機匣的軸向失穩壓力;材料3～材料1，近似認為Eθ不變化，軸向彈性模量Ex逐漸增大，但軸向失穩壓力卻逐漸減小，這是由于做無量綱的時候將Ex作為分母導致的，引入以Eθ為基準的軸向失穩壓力［18］:

材料3～材料1，近似認為Eθ不變，因此以Eθ為基準的無量綱是合理的，圖5為以Eθ為基準的無量綱軸向失穩壓力和周向波數的關系圖，通過圖5(a)我們發現隨著Ex的增大，機匣的軸向失穩壓力P'cr也隨之增大。

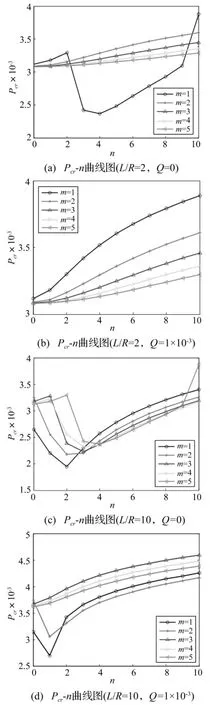
圖3 長徑比和徑向壓力對臨界失穩壓力的影響Fig.3 Effects of length－diameter ratio and radial pressure on critical buckling pressures

圖6(a)和圖6(b)為厚徑比和徑向內壓對失穩壓力和周向波數的影響，厚徑比(h/R)的增大和徑向內壓的存在能顯著提高失穩壓力。

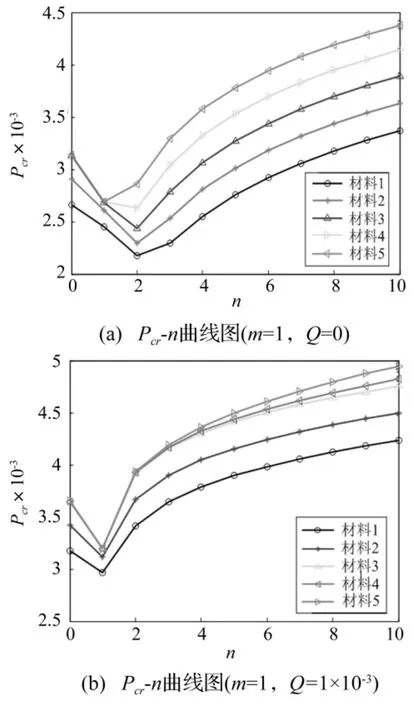
圖4 材料參數和徑向壓力對臨界失穩壓力的影響Fig.4 Effects ofmaterial parameters and radial pressure on critical buckling pressures

圖5 以Eθ為無量綱基準下徑向壓力對臨界失穩壓力的影響Fig.5 Effects ofradial pressure on critical buckling pressures with Eθas the benchmark of dimensionless

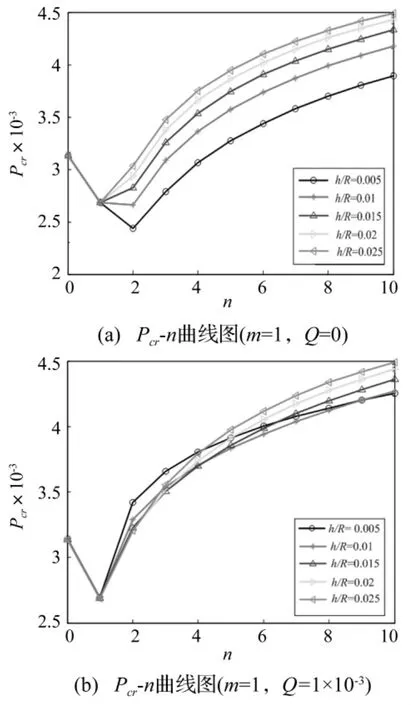
圖6 厚徑比和徑向壓力對臨界失穩壓力的影響Fig.6 Effects of thickness－radius ratio and radial pressure on critical buckling pressures

3 徑向簡諧激勵下機匣的振動特性分析

將圓柱殼的振型表示為軸向梁函數和周向三角函數組合的一般解形式［19］:

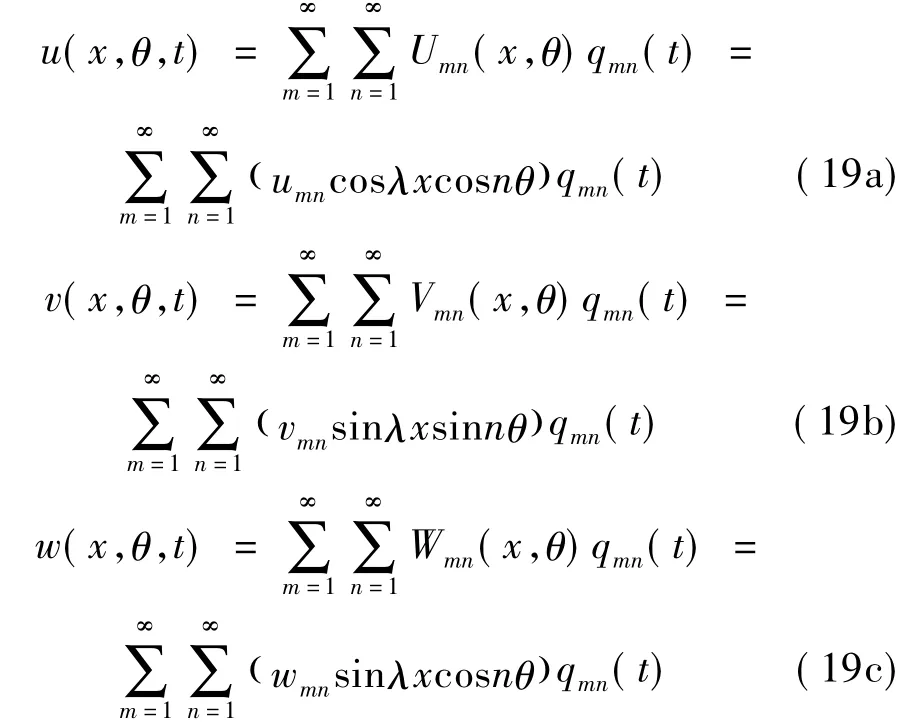
式中:Umn，Vmn，Wmn為廣義振型函數，qmn(t)為廣義坐標，n為周向波數。

將式(3)，式(4)，式(5)，式(19)代入式(2)，得:

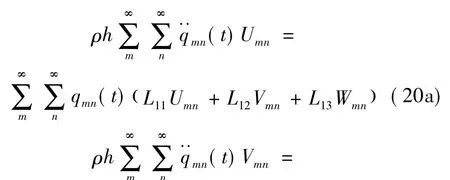
從式(29)可知，在簡諧激勵作用下，機匣三個方向的位移響應是各種振型疊加的結果，其中αmn，βmn分別表示軸向和周向與徑向的振幅比，對于不同的振型m，n，存在不同的振幅比。

以三種不同材料(見表1)為例，研究徑向簡諧激勵對機匣穩態動力響應的影響，設徑向簡諧激勵作用在機匣L/2處，激勵為p eiωt，機匣的幾何參數為:L/R= 10，h/R=0.01。

圖7(a)和圖7(b)為激勵面內的位移響應曲線，圖7(a)中給出了第6，第7個峰值處的放大圖，其峰值分別用A，B表示，振型m=1，n=4和m=3，n=7也分別標注在圖中，可以看出固有頻率對應的響應值并不是系統實際響應的峰值，與峰值略有偏差，共振峰值與固有頻率有微小偏差的現象，是由于模態耦合的原因導致的。Leissa［20］在討論圓柱殼受到正弦波激勵的穩態響應問題時指出了這個現象。

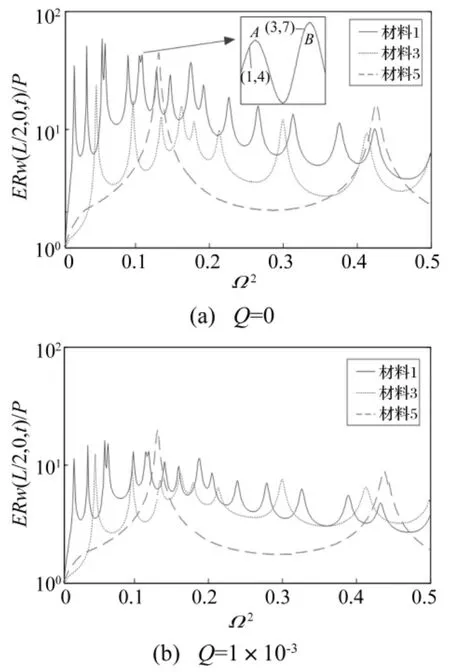
圖7 激勵面內徑向位移響應曲線Fig.7 Diagram of radial displacement in excitation forced plane

從對比圖7(a)和圖7(b)，圖8(a)和圖8(b)可知，徑向內壓的存在，導致機匣的共振頻率升高，當外激勵頻率高于無內壓作用的機匣的固有頻率時才會引起殼體共振;通過圖7(a)和圖8(a)可知，在徑向簡諧激勵p(t)f1(x0)作用下，機匣在非激勵面內，徑向位移響應的最大值發生在基頻率處，而激勵面內響應的最大值發生在第3階固有頻率處，徑向內壓的存在，使激勵面內和非激勵面內的徑向位移響應的幅值有所減小。

圖8 非激勵面內徑向位移響應曲線Fig.8 Diagram of radial displacement in non－excitation forced plane

4 結論

采用Flügge殼體理論，分析了徑向內壓作用下復合材料機匣的彈性穩定性，討論了結構尺寸以及材料特性對屈曲特性的影響。并應用振型疊加方法，分析了復合材料機匣在徑向內壓作用下受到徑向簡諧激勵作用時穩態動力響應問題。結論如下:

(1)在強度允許的范圍內，徑向內壓的提高有助于提高機匣的抗屈曲能力。

(2)徑向內壓的存在，提高了機匣的共振頻率，即當激勵頻率高于無內壓作用的機匣的固有頻率時才能引起共振;在徑向簡諧激勵作用下，由于模態耦合的原因，共振曲線峰值和固有頻率點存在微小偏差。在徑向簡諧激勵p(t)f1(x0)作用下，機匣徑向位移的最大值在激勵面內和非激勵面內對應的頻率點不同，激勵面內，最大響應發生在第3階頻率點，而在非激勵面內，卻在基頻處出現最大值。

［1］陳予恕，張華彪.航空發動機整機動力學研究進展與展望［J］.航空學報，2011，32(8):1372－1391.

CHEN Yu－shu，ZHANG Hua－biao.Review and prospect on the research of dynamics of complete areo－enginesystems［J］.Acta Aeronautica et Astronautica Sinica，2011，32(8):1371－1391.

［2］航空發動機設計手冊總編委會.航空發動機設計手冊(第17分冊)載荷及機匣承力件強度分析［M］.北京:航空工業出版社，2000.

［3］沈惠申.正交鋪設層合圓柱在外壓作用下的屈曲和后屈曲［J］.上海交通大學學報，1992，26(1):66－72.

SHEN Hui－shen.Buckling and postbuckling of cross－ply laminated cylindrical shells under external pressure［J］.Journal of Shanghai Jiaotong University，1992，26(1):66－72.

［4］卓曙君，等.復合材料加筋柱殼的穩定和振動相關性研究［M］.北京:北京大學出版社，1998.

［5］Breivik N L，HyerMW.Buckling and postbuckling behavior of curved composite panels due to thermal and mechanical loading［C］//Proceeding of the American Society for Composites 11thTechnical Conference，1996:80－89.

［6］Simitses G J，Sheinman I，Shaw D.The accuracy of Donnell's equations for axially－loaded，imperfect orthotropic cylinders［J］.Computers and Structures，1985，20(6):939－949.

［7］仲政，吳林志，陳偉球.功能梯度材料與結構的若干力學問題研究進展［J］.力學進展，2010，40(5):528－541.

ZHONG Zheng，WU Lin－zhi，CHEN Wei－qiu.Progress in the study on mechanics problems of functionally graded materials and structures［J］.Advances in Mechanics，2010，40(5):528－541.

［8］Jones R M.Effect of prebuckling of deformations on buckling of laminates composite cylindrical shells［D］.Texas.Southern Methodist University，1975.

［9］唐文勇，王天霖，張圣坤.徑向載荷作用下復合材料圓柱殼的非線性動力屈曲［J］.振動與沖擊，2006，25(2):155－192.

TANG Wen－yong，WANG Tian－lin，ZHANG Sheng－kun.Nonlinear dynamic buckling of composite cylindrical shells under radial loads［J］.Journal of Vibration and Shock，2006，25(2):155－192.

［10］齊紅宇，溫衛東，王林江，等.航空發動機復合材料機匣在軸向壓力和內壓耦合作用下屈曲特性的有限元分析［J］.玻璃鋼/復合材料，2002(3):15－18.

QIHong－yu，WENWei－dong，WANG Lin－jiang，et al.Fea method for critical buckling load of aeroengine composite case［J］.Fiber Reinforced Plastics/Composites，2002(3):15－18.

［11］齊紅宇，溫衛東.復合材料及發動機機匣的屈曲與疲勞研究［D］.南京:南京航空航天大學，2001.

［12］李健，郭星輝，楊坤，等.軸向運動復合材料圓柱殼的非線性振動研究［J］.固體力學學報，2011，32(2):176－185.

LI Jian，GUO Xing－hui，YANG Kun，et al.Study on the nonlinear vibration of axially moving cylindricalshells made from composites［J］.Chinese Journal of Solid Mechanics，2011，32(2):176－185.

［13］瞿葉高，華宏星，諶勇，等.復合材料旋轉殼自由振動分析的新方法［J］.力學學報，2013，45(1):139－143.

QU Ye－gao，HUA Hong－xing，CHEN Yong，et al.A new method for free vibration analysis of composite laminated shells of revolution［J］.Chinese Journal of Theoretical and Applied Mechanics，2013，45(1):139－143.

［14］陳強，強寶民，何潤生.幾種參數對復合材料圓柱殼體振動特性的影響［J］.中國工程機械學報，2007，5(4):394－398.

CHEN Qiang，QIANG Bao－min，HE Run－sheng.Parametric impacts on vibration performance of composite cylindrical casing［J］.Chinese Journal of Construction Machinery，2007，5(4):394－398.

［15］李戎，梁斌，Noda N，等.基于波動法的靜水壓力下功能梯度圓柱殼振動特性研究［J］.船舶力學，2013，17(2): 148－154.

LIRong，LIANG Bin，Noda N，et al.Study on vibration of functionally graded cylindrical shells subjected to hydrostatic pressure by wave propagation method［J］.Journal of Ship Mechanics，2013，17(2):148－154.

［16］劉敬喜，譚安全，李天勻，等.復合材料層合圓柱殼中振動功率流特性［J］.哈爾濱工程大學學報，2012，33(3): 269－274.

LIU Jing－xi，TAN An－quan，LI Tian－yun，et al.Characteristics of the vibration power flow in a laminated composite cylindrical shell［J］.Journal of Harbin Engineering University，2012，33(3):269－274.

［17］Dong SB.Free vibration of laminated orthotropic cylindrical shells［J］.Journal of the Acoustical Society of America，1968，44(9):1628－1635.

［18］Librescu L.Refined geometrically nonlinear theories of anisotropic laminated shells［J］.Quarterly of Applied Mathematics，1987，45(1):1－22.

［19］李學斌.正交各向異性圓柱殼靜動態特性及比較研究［D］.武漢:華中科技大學，2004.

［20］李學斌.正交各向異性圓柱殼的穩態動力響應分析［J］.船舶力學，2007，11(1):79－87.

LI Xue－bin.Harmonic response analysis of orthotropic cylindrical shells［J］.Journal of Ship Mechanics，2007，11 (1):79－87.

［21］Leissa AW，Iyer K M.Modal response of circular cylindrical shells with structural damping［J］.Journal of Sound and Vibration，1981，77(2):1－10.

Elastic stability and vibration characteristics of a composite case

WEN Deng－zhe1，CHEN Yu－shu1，HOU Lei1，LIZhong－gang2
(1.School of Astronautics，Harbin Institute of Technology，Harbin 150001，China;
2.School of Mechatronic Engineering，Harbin Institute of Technology，Harbin 150001，China)

Influences of radial internal pressure on elastic stability(buckling characteristics)of a composite case were analyzed based on the Flügge shell theory，in addition，influences of its geometric parameters andmaterial properties on its buckling characteristicswere also discussed.Results showed that increasing the internal pressure can improve the anti－buckling ability of the casewithin the limits of its strength.Furthermore，the dynamic responses of the composite case under a radical harmonic force were studied by applying the mode superposition method.It was shown that under the radial harmonic excitation，the frequencies of the maximum radial displacements in the excitation force plane and in the non－excitation forced plane are different;more specifically，themaximum radial displacement in the excitation force plane appears at the 3rd modal frequency of the case，but that in the non－excitation force plane appears at the fundamental modal frequency of the case.

composite case;cylindrical shell;elastic stability;mode superposition method

O323

A

10.13465/j.cnki.jvs.2015.23.001

國家自然科學基金資助項目(10632040/11302058)

2014－05－07修改稿收到日期:2014－11－19

溫登哲男，博士生，1986年生

陳予恕男，教授，博士生導師，中國工程院院士，1931年生