注重引導，構建“思維性”課堂

張志剛

摘 要：獨立靈活的數學思維在高中數學學習過程中有著舉足輕重的地位。思維是數學的靈魂，構建“思維性”課堂是當前高中數學教學的重要任務。本文結合教學實際，對于引導學生形成數學思維的若干方法進行了簡要闡述。

關鍵詞：高中 數學 思維

在當前的數學教學中，“教師講什么，學生跟著學”的傳統教學方式仍然廣泛存在。這種方式雖然可以使課堂教學過程完全按照教學計劃進行，卻完全忽略了學生數學靈活思維的發展。數學學習進入到高中階段，知識內容明顯繁雜深入了許多，全部依靠教師逐一講解是不現實的。高中數學教學過程中，除了知識內容本身之外，更為重要的教學目標是對學生數學思維方式的培養。

一、設置懸念，引發思維開啟

“思維性”課堂的構建，最重要的就是學生的自主思維在整個數學課堂教學中的發揮。因此，教師所需要落實的第一步，便是讓學生意識到其獨立思維的存在，啟發學生思維，使其開始活躍起來。我們常說的優化課程導入，意義也多在于此。在實際教學當中，經常采用設置懸念的方式引導學生思維開啟，效果比較理想。

例如，在高中《數學》“函數概念與基本初等函數”當中，學生們將細致地學習函數的知識內容。函數是高中數學當中一個十分重要的部分，概念學習作為知識點的基礎尤為重要。然而，因數學概念的語言表達不同于日常用語，較難激發學生們的學習興趣。于是，筆者在上課伊始便向學生設置了一個懸念：首先向學生們展示了從1949～1999年我國人口數據的表格（如表）。乍看之下，這些數據之間沒有任何聯系，而筆者卻告訴學生，通過本章將要學習的數學方法，不僅能夠量化體現出其中的對應關系，還能夠由此科學地預測出今后幾年我國的人口數量。學生們感到十分驚訝，頓時對這個神奇的知識內容產生了興趣。緊接著，筆者又進一步啟發學生，如果已知一個物體從靜止開始下落，其下落距離y（m）與下落時間x（s）之間滿足關系式y=4.9x2，能求出當物體下落5s時的下落距離嗎？學生們漸漸開始明白，這之間存在著一個一一對應的關系，同時，也開始動手計算，實際體驗隱藏在函數關系式背后的對應關系了。

1949～1999年我國人口數據表

設置懸念的好處在于：一方面，其形式與內容能夠有效激發起學生們的好奇心，從而主動關注懸念所指問題；另一方面，在懸念的引導之下，學生們開始很自然地進行思考，嘗試為自己心中的問題尋找答案。在這個過程當中，學生們的自主思維已經逐漸開啟了。

二、放開禁錮，激發思維活動

在數學學習過程中，學生們為何會失去靈活思維的主動性？很大一部分原因在于教師對于學生思維的束縛過于沉重。在很多教師看來，按部就班地完成教學計劃中的內容才是最重要的，因此，需要時刻抓住學生的思維方向，使之依據教師既定的正確軌道行進。實際上，這樣的做法反倒讓預期的教學目標無法真正實現。

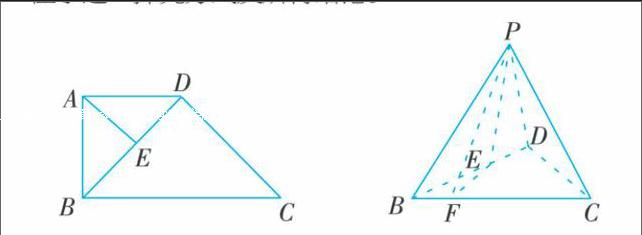
例如，在高中數學立體幾何的學習當中，折疊問題是一類十分典型的提問方式。在解答這類問題時，根據折疊的具體方式來把握其中不變的數量部分是最為關鍵的一個環節，也在無形中增加了很多已知條件。筆者并沒有直接將這個思維方法提供給學生，而是先出了這樣一道題目：在四邊形ABCD中，已知AD∥BC，且AD=AB，∠DCB=45°，∠DAB=90°。現將△ADB沿著DB折疊至點P，使得面DBP與面DCB垂直（如下圖）。求證：面CDP⊥面BCP。學生們通過實際折疊紙張模擬題目中的折疊過程，很快發現了其中的等量關系。雖然耗費了一些時間，但卻使學生牢牢記住了這一探究方式及所得結論。

由此可見，學生們的數學思維不是不靈活，只是缺乏展現其靈活性的機會。教師平時對學生的思維禁錮過多，常常使學生自己都忘記了思維的存在。這就是很多學生離開課本或是面對稍加變形的問題就無從下手的原因。教師應適當放手，給學生提供一個自由思維的空間。

三、合作交流，點燃思維火花

僅靠學生一己之力進行思考，往往力量過于單薄，無法將學生的思維靈活性全部激發出來。但若全部憑借教師一方進行引導，學生的思維廣度不免受到限制。因此，教師需要找到一個合適的方式，既能開闊學生思維，又能讓學生的學習輕松愉快。將學生分組，在小組合作的基礎上交流溝通，不失為一個好方法。

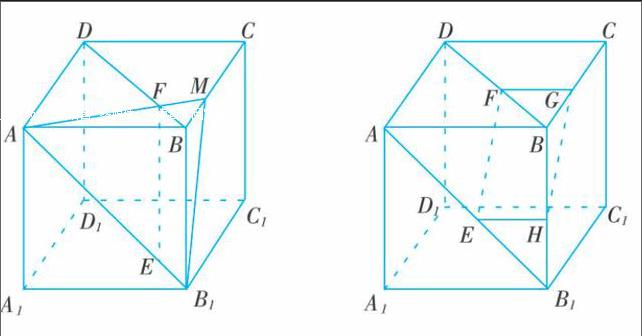
例如，在高中數學學習中，學生陸續學習了立體幾何的相關知識。在立體幾何中，空間之中平行關系的相互轉化是一個十分重要的內容。為了讓學生深刻理解這部分的知識并且能夠對其中的思想方法靈活運用，筆者首先將“線面平行”與“線線平行”的判定方法以及轉化思路等內容總結給學生。然后，筆者向學生提供了一道習題，難度不算太大，但是要求學生用兩種不同的方法進行解答：在正方體ABCD-A1B1C1D1中，已知點E在棱AB1上，點F在棱BD上，并且滿足B1E=BF。請證明：EF與面BCC1B1平行。在小組討論的過程當中，學生首先認可這道題目是一個從“線線平行”到“線面平行”的證明過程。很快有學生依據筆者之前所總結的方法，利用平行線分線段成比例定理的推論完成了證明（如下面左圖）。第二種方法可讓大家犯了難。“到底怎樣才能出現平行呢？”“用幾何圖形構造一個行不行？”很快地，通過構造平行四邊形證明“線線平行”的方法出現了（如下面右圖）。

在小組合作的氛圍下，學生的思維積極性大增。由于討論的同伴是一起學習的同學，大家的知識起點與理解深度相近，所得出的想法更便于學生理解與接受。另外，在熱烈的學習氛圍中，學生也更加勇于表達自己的想法。在不斷迸發的思維火花當中，學生的思維廣度被大大拓寬了。

四、及時評價，提升思維深度

知識內容本身的教學并不是課堂教學的終點，一個及時有效的評價作為課堂教學的收尾顯得至關重要。在評價的過程中，包含了教師在實際教學過程當中，所觀察到的學生們在使用知識及思想方法等方面所存在的問題，及時指出并且引導學生盡快更正，同時也包含了教師通過學生反饋而發現的自身教學計劃在實施過程中所出現的漏洞，進而繼續完善教學思路，使得接下來的教學活動更為高效。

例如，在高中數學中，一個很重要的內容是函數的單調性。在課程進行當中，教師并沒有直接告知學生應當如何判斷函數的單調性，而是通過反復強調遞增函數與遞減函數的定義與特點來啟發學生，使其獨立思考出函數單調性的判斷方法。最后，學生們得出結論：先取值，再作差，經過變形之后確定符號，然后就可以得出關于函數單調性的結論了。這個思維過程并無明顯錯誤，但是，仔細留心便會發現，學生們在思考過程中完全忽略了對于函數單調區間的強調。于是，在課后評價當中，筆者向學生們展示了如下圖中的幾個函數圖像，并且提問：如何來描述這些函數的單調性？學生們馬上意識到，原來函數不一定是一直遞增或是一直遞減的。由此，大家也再次認識到了單調區間這一概念在函數單調性判斷中的重要性。

從以上實例可以看出，一次成功的評價離不開教師在實際教學過程中的細致觀察，既要通過觀察學生的表現分析學生的想法，還要抓住學生思維的不足及時提出，并幫助其修正。可以說，在評價的過程當中，教師更像是學生的一面鏡子，幫助學生發現學習當中的漏洞，并指導其及時填補，保證其“數學思維”的有效性與完整性。

“思維性”課堂的構建，需要教師有意識地對學生進行引導。首先，要創造適當的機會，讓學生意識到“數學思維”的存在。然后，通過課堂教學方式的巧妙選擇，不斷讓學生的思維活躍起來。最后，借助及時有效的評價，為學生剛剛進行的思維活動指出不足、引導完善，實現對其“數學思維”的提升。長此以往，學生的數學思維方式得以有效建立，對相關思維方法的掌握也會有顯著進步，對于高中階段乃至日后更為深入的數學學習都是大有裨益的。

參考文獻

[1]林軍.數學課堂應注重“思維”教學[J].中學生數理化（學研版）2011（11）.

[2]李蘭萍.構建思維性課堂 彰顯數學的美麗[J].教書育人2014（2）.

[3]談志彪.激活學生的創新思維[J].新課程（下）2011（2）.