基于中心流形理論的風力發電系統 非線性控制策略研究

劉 軍 段 韜

（西安理工大學自動化學院，西安 710048）

由于永磁同步風力發電系統具有機械損耗小、運行效率高、安全可靠、便于維護等優點，近年來，得到了廣泛的運用。

永磁同步風力發電系統的最大風能跟蹤通常采用PI 控制器，雖然PI 控制對系統內部參數的變化和外部干擾具有一定的適應能力，但是由于控制器參數是固定值，所以當外部干擾較大時，系統的性能會受到較大影響，甚至不穩定[1]。

在現代控制理論與應用中，線性系統占據非常重要的位置，其基本理論已發展得相當完善。但是實際的系統絕大多數都是非線性的，對外部擾動和參數變化也比較敏感，控制效果往往不理想。

近幾十年來，以微分幾何和微分對策為基礎的非線性控制理論快速發展，其中非線性系統的零動態線性化設計方法，因其構思比較巧妙，往往能得到較好的設計效果[2]。

由于滑模變結構控制具有對干擾的不變性和降階特性等特點，越來越受到人們的重視。在常規的反饋控制器上加上滑模變結構控制，可以提高系統的抗干擾能力。

因此，本文把兩種方法相結合，運用于永磁同步風力發電機最大風能跟蹤控制上，既可以減少系統對精確數學模型的依賴性，同時線性化也有助于建立線性滑模函數。

1 風力發電系統模型

1.1 風速模型

風力發電系統中，組合風速可以較好的反映自然風速的特性，尤其是在風速突變時，能夠全面地檢驗風力發電系統的性能，乃至整個系統的抗干擾性[3]。

組合風速中，可將自然風速v分為基本風速vb、陣風vg、漸變風vr和噪聲風vn。其數學模型為

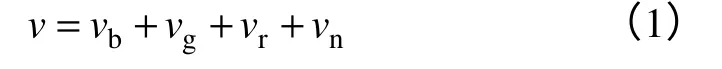
1.2 風力機模型

風力機是用來捕獲空氣動能并轉換為機械能，其工作性能決定了整個風力發電系統的有效輸出功率且直接影響到機組的安全穩定運行。

永磁同步風力發電機轉子的運動方程為

式中，J為發電機轉子和風力機的總轉動慣性系數；Tωt為發電機輸入的機械轉矩；Tg為發電機輸出的電磁轉矩；ωg為電機轉速。

風力機輸入的機械轉矩為

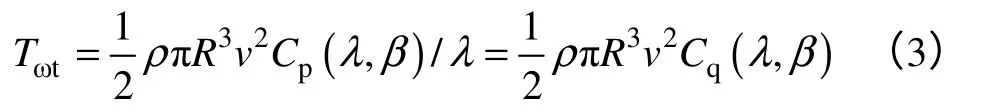
式中，ρ為空氣密度；R為風輪半徑；v為風速；Cp為風能利用系數；λ為葉尖速比；Cq為風機非線性轉矩系數；β為槳距角。

文獻[4-5]指出風機的非線性轉矩系數Cq可以用葉尖速比λ的六次多項式擬合來表達。Tωt的六階表達式比較復雜，計算量大，為了計算方便，忽略啟動過程，可用一個二階多項式近似代替。

二階方程已經很好的描述了最佳工作狀態附近λ的特征[6]。

發電機輸出的電磁轉矩為

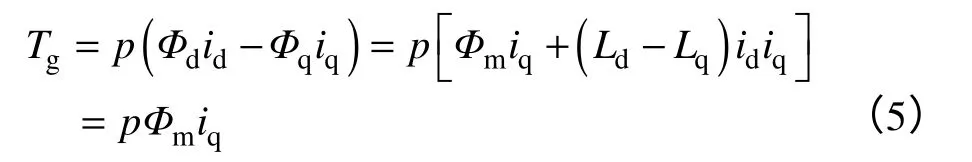
式中，p為極對數；Φd、Φq為d、q 軸的磁通；Ld和Lq為定子d 軸和q 軸電感，同時Ld=Lq=L；id和iq為定子d 軸和q 軸電流；Φm為永磁同步電機磁通。

1.3 風力發電系統模型

在dq 同步旋轉坐標系下，永磁同步發電機的模型如下

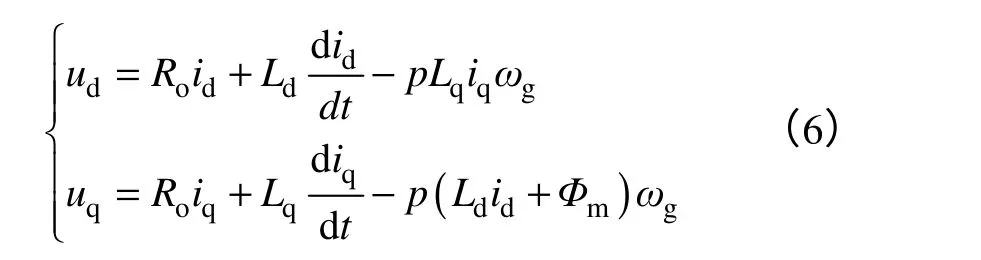
式中，Ro永磁同步電機定子電阻。

設永磁同步風力發電系統的簡化結構如圖1所示。

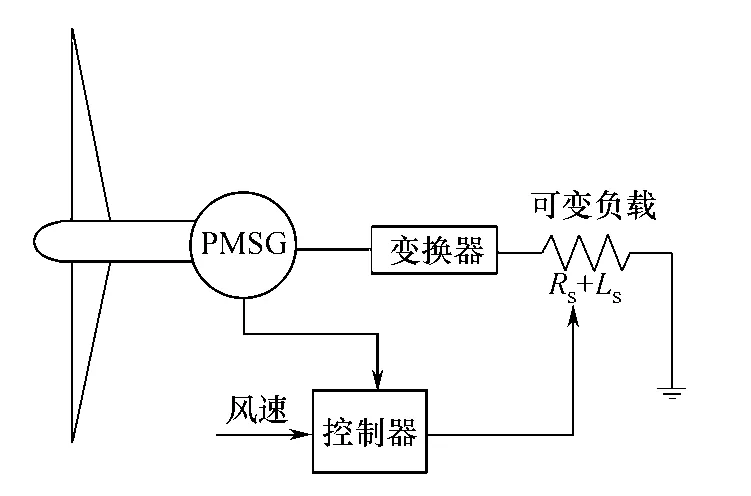
圖1 永磁直驅風電系統等效模型

該控制系統的簡化結構基于以下考慮[7-8]：

1）本文研究的重點在于最大風能跟蹤控制，并且假設其他部分都正常工作。

2）風電系統的電氣動態遠遠比機械動態快，根據奇異攝動系統理論[9]，各子系統的動態響應速度相差較大時，研究的“慢”動態子系統時，可以忽略“快”子系統的動態影響，認為其響應瞬間完成，其值始終處于“準穩態”。

3）風力發電系統的功率經過變流后，網側相當于負載，故簡化為等效阻抗Rs和Ls表示。

根據式（2）～式（6），直驅永磁風力發電系統的整體動態特性數學模型為

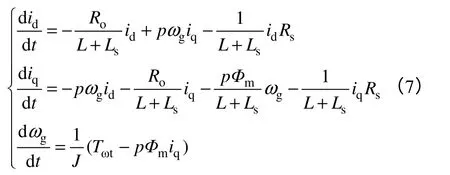
式中，Rs和Ls為等效阻抗，Rs為可變電阻，Ls為定電感。

2 系統的控制策略

2.1 PI 控制

風力發電系統的機側控制主要有轉速環PI 控制和功率環PI 控制，其具有設計簡單和適應性好等特點，但永磁同步電機的強非線性使PI 參數難以整定，給實際運用帶來了一定困難[10]。風力發電系統機側轉速和功率PI 控制系統結構圖如圖2和圖3所示。 圖中，G(s)發電機和變流器動態簡化為的傳遞函數。

圖2 轉速PI 控制框圖

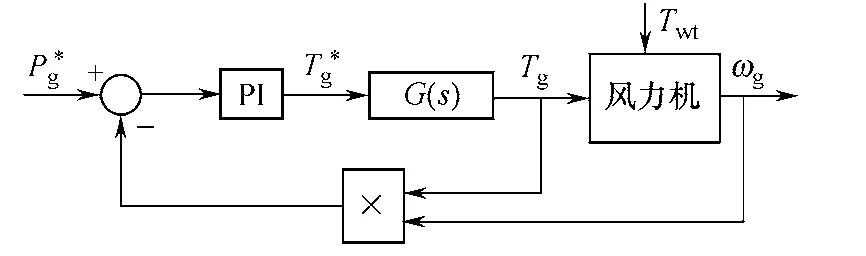
圖3 功率PI 控制框圖

2.2 中心流形理論

如果S是一個光滑的子流形，且局部不變，S在x=0 的切空間恰為由A 的零實部特征值所對應的特征向量所張成，則稱流形S是系統所在的中心流形。對中心流形定理介紹如下[11]：

考慮非線性系統（8）

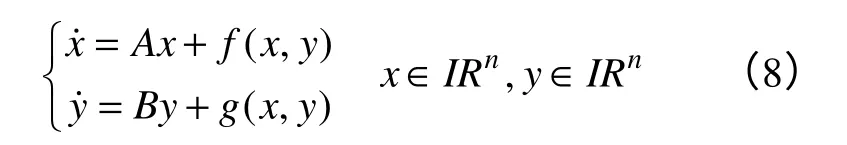
式中，f、g為充分光滑函數。

f(0,0)=0,g(0,0)=0,Dx(0,0)=0,Dfx(0,0)=0,Dfy(0,0)=0,Dgx(0,0)=0,Dgx(0,0)=0。A，B 分別為n×n,m×m矩陣，其的特征根分別有零實部和負實部，(0，0)是系統的一個平衡點。

定理1：如果f(x,y)和g(x,y)屬于Ck（k次可導函數，k≥2），那么存在一個中心流形y=h(x)使之屬于Ck-1。將中心流形y=h(x)帶入式（8）中得到n維約化系統：

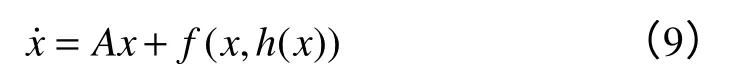
定理2：如果約化系統式（9）的平衡點是局部穩定（不穩定、漸進穩定）的，那么原系統式（8）的平衡點也是局部穩定（不穩定、漸進穩定）的。將式（8）代入式（9），得到h(x)，應滿足方程

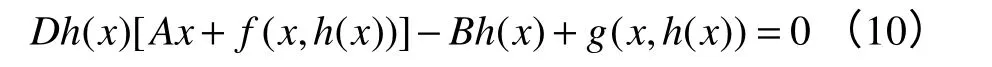
同時，h(0)=0,Dh(0)=0。

實際運用當中，h(x)不能由式（10）精確求解，但是通過定理3 能得到h(x)一定精度的近似解。

定理3：假設有C1函數φ：IRn→IRm，它滿足φ(0)=0，Dφ(0)=0，且有某個常數p＞1，使得N(φ(x))=O(|x|p)在x→0 時，h(x)=φ(x)+O(|x|p)。

2.3 基于中心流形理論的零動態原理及其設計[12]

在非線性系統零點平衡狀態問題上，中心流形理論可以為非線性系統在臨界情況下進行穩定性設計。而實際工程中，傳統的零動態設計方法難以使系統的輸出量在任何時刻都保持在零值。所以為了克服傳統零動態設計方法的缺點，采用中心流形理論并結合狀態反饋線性化方法，設計新的零動態。

文獻[13]在推導出永磁同步電動機數學模型的基礎上，應用中心流形定理，得到了其簡化的中心流形方程，并在此基礎上討論了其穩定性及其分支情形。

考慮系統（8），輸入函數

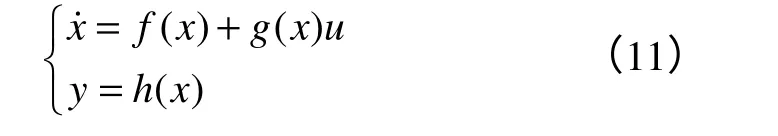
y=h(x)相對于系統輸入u的關系度r小于系統階數n。通過坐標變換z=φ(x)和反饋v=a(ε,η)+b(ε,η)的作用，可以把系統(11)變換為

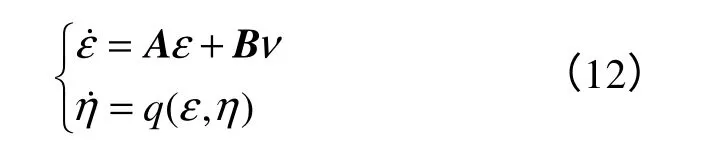
式中

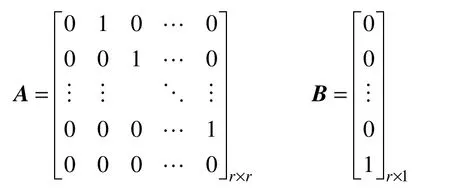
同時，若零動態=q(0,η)在η=0 處漸進穩定，則在線性控制律u*中，線性系統=Aε+Bv可以在(ε，η)=(0，0)處鎮定系統（11）。

選取狀態變量x=[x1,x2,x3]T=[id,iq,ω]T，控制輸入為u=Rs，輸出為轉速y=ωg，對式（4）化簡

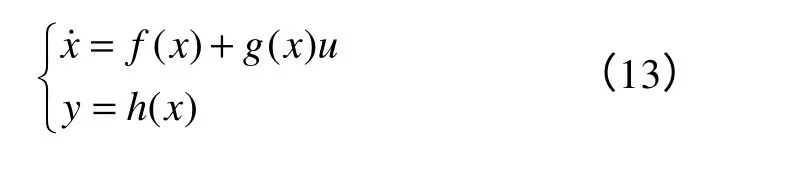
其中

對函數h(x)進行李導數遞推運算，則有

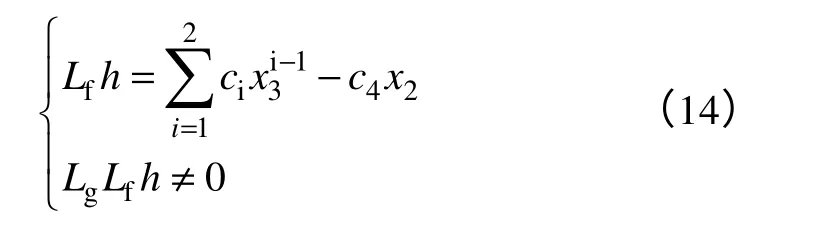
系統的相關度為2＜3，只能實現部分線性化，故采用零動態設計原理。

先進行Z坐標變換z=Φ(x)

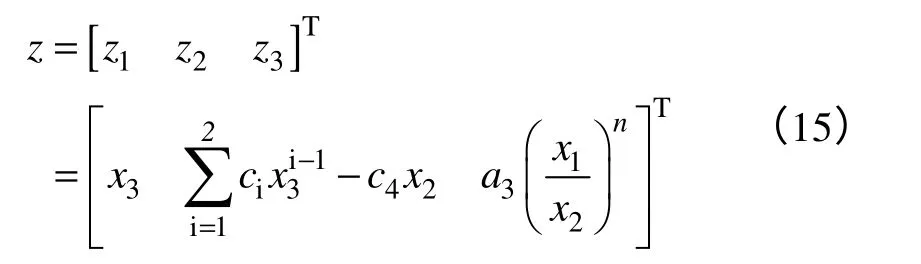
式中，冪次n可以取任意值。

采用基于中心流形理論的零動態計算方法，原非線性系統狀態方程式（13）經過變換得到線性系統狀態方程式（16）：

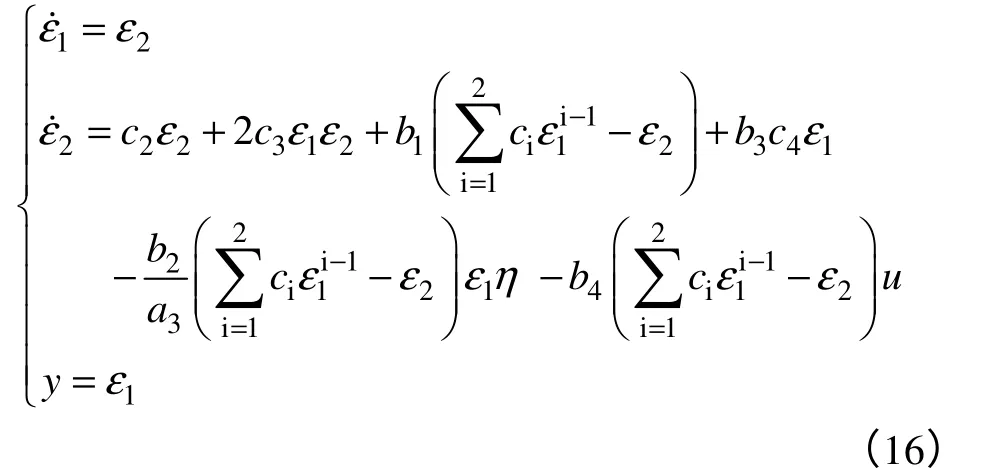
式中，ε1=z1,ε2=z2,η=z3。若記ε=[ε1,ε2]T，則上述線性系統可進一步寫為

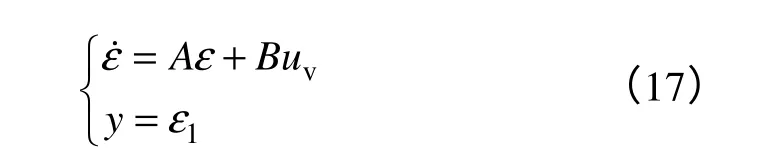
式中，非線性系統的輸入變量u與線性系統的輸入變量uv具有以下關系

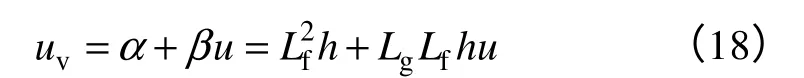
其中

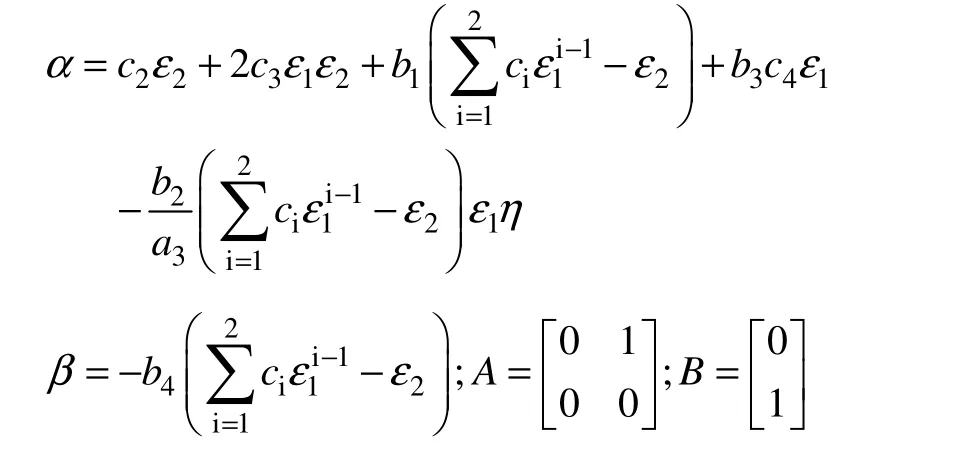
2.4 滑模控制器設計

針對系統

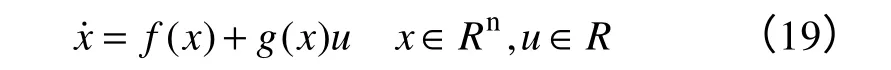
其中x滿足=xi+1,i= 1,… ,n-1。滑模面設計為

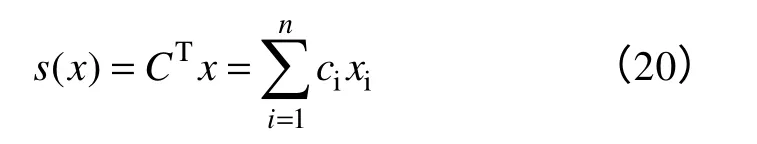
式中，x為狀態向量，C=[c1…cn-11]T。

參數ci應該滿足多項式pn-1+cn-1pn-2+…+c2p+c1，其中p為Laplace算子[14]。

風力發電機一般以發電機轉速ωg作為控制目標，風電系統根據風速和輸出功率等條件可以得到發電機參考轉速ωref，設為轉速誤差，則有

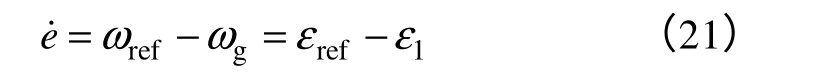
可取線性切換函數為

則可以得到滑動模型運動方程

因此，只要保證ki＞0，i=0,1，即可保證滑動模態漸進穩定，調節k的取值，可調節滑動模態的動態品質。

取Lyapunov 函數為

則

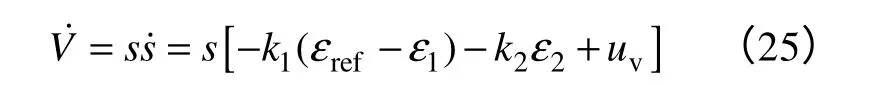
采用新型指數趨近律，有

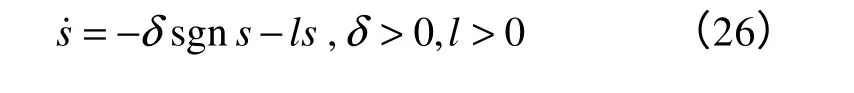
可得到線性系統的輸入變量uv：

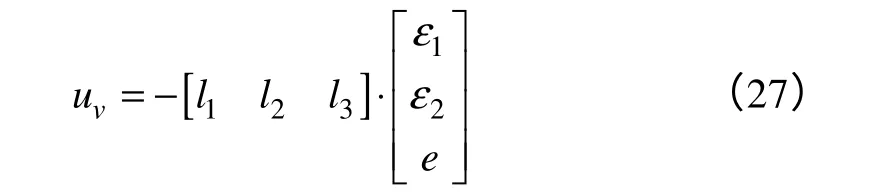
所以由式（18）可得到

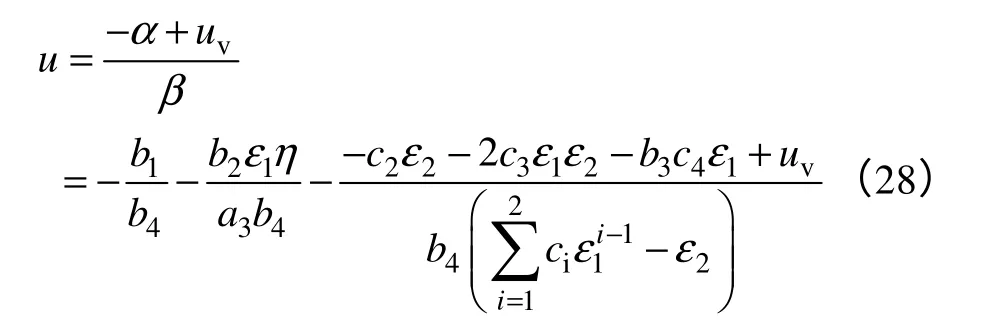
上述分析可作出最大風能跟蹤的控制框圖4。

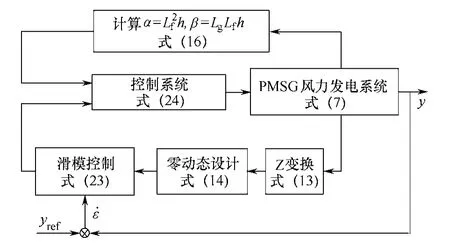
圖4 風力發電系統控制系統框圖

3 仿真結果分析

為了驗證提出算法的有效性，本文基于Matlab/Simulink 建立了仿真模型，主要參數見表1。

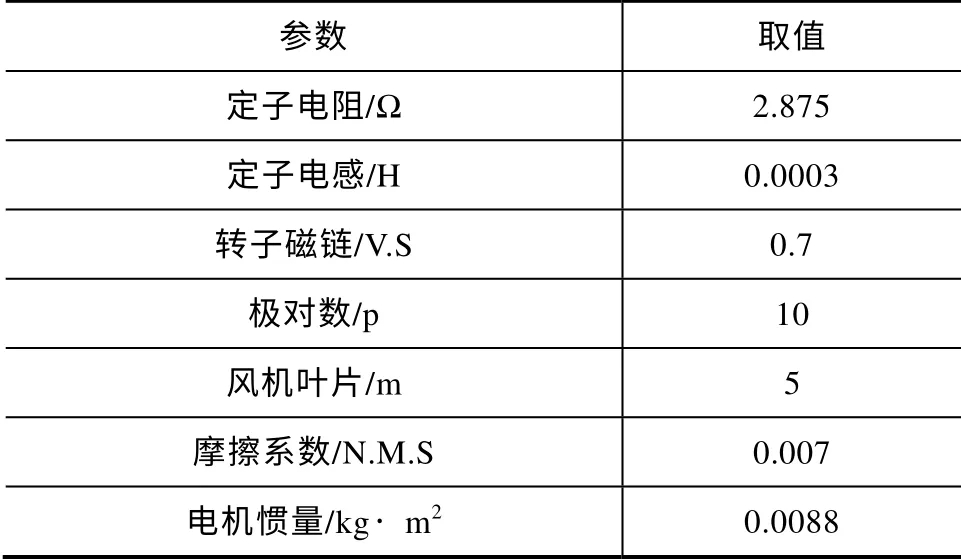
表1 系統主要參數

3.1 階躍風下的仿真圖

階躍風下，初始時，風速v=6m/s在30s后階躍到v=9m/s，在65s后下降到v=8m/s。

圖5為最大風能利用系數Cp在兩種控制方法的對比仿真圖。其中，虛線為PI控制，實線為基于中心流形理論零動態設計的滑模控制。

圖6為基于兩種控制方法下實際轉速和參考轉速的對比仿真圖。

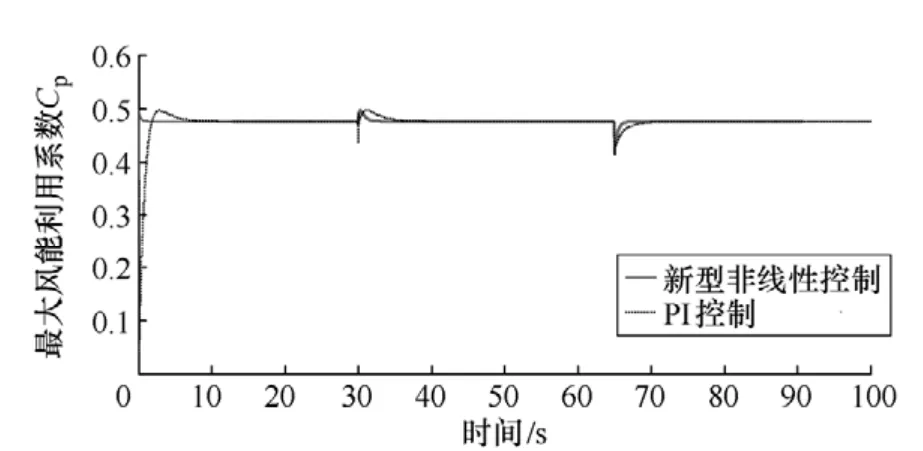
圖5 最大風能利用系數Cp 在兩種控制方法的 對比仿真圖

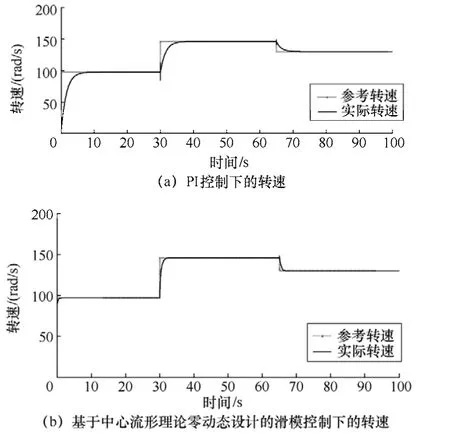
圖6 兩種控制方法在階躍風下的轉速對比

從圖中可以看出，在PI控制中，其轉速響應時間明顯滯后于基于中心流形理論零動態設計的滑模控制的響應時間。

3.2 組合風下的仿真圖

在組合風速中，設基本風速vb=6m/s 陣風的最大值vgmax=2m/s、漸變風vrmax=2m/s 和和噪聲風的變化范圍vn=±2m/s。其風速曲線如圖7所示。

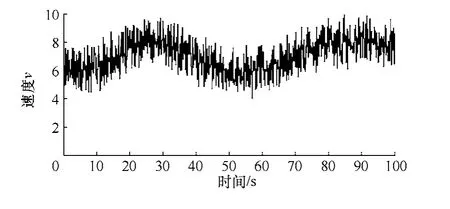
圖7 組合風

在組合風速下，兩種控制方法的轉速曲線如圖8所示。

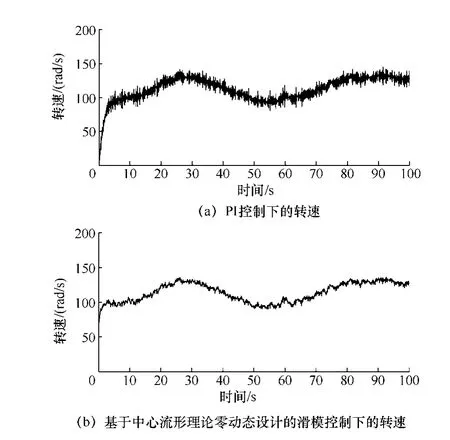
圖8 兩種控制方法在組合風下的轉速對比

圖中可以看出，在組合風速下，與PI 控制相比較，基于中心流形理論零動態設計的滑模控制下的電機轉速震蕩較弱，且波動較小，恢復速度快，充分說明了該新型非線性控制方法具有良好的動態性能和魯棒性。

3.3 轉速與輸入阻抗關系

在本文中，網側相當于負載，簡化為等效可變電阻Rs和定電感Ls表示。Rs的不同也會影響著轉速的變化。

圖9是基于中心流形理論零動態設計的滑模控制下，轉速與輸入電阻Rs關系。

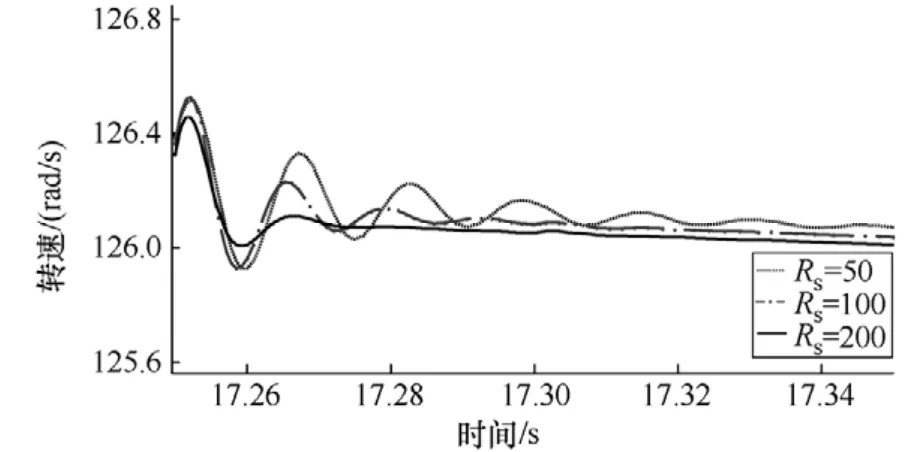
圖9 轉速與輸入阻抗關系

從圖中可以看出，由于風機重負載的阻礙作用，控制輸入Rs越大時，轉速的波動越小，抗干擾能力越強。

綜上，通過仿真可以驗證本文針對直驅永磁同步電機，提出的基于中心流形理論的零動態設計滑模變結構控制方案是正確可行的，該控制方案不僅具有響應速度快，超調小等優點，而且具有較強的抗擾性能。

4 結論

本文針對實現最大風能跟蹤的問題，提出基于中心流形理論的零動態設計與滑模變結構相結合的控制策略。階躍風和組合風下，與PI 控制相比，該控制器明顯提高了系統的動態性能，而且階躍響應迅速，超調較小，抗擾動性能好，具有較強的魯棒性。

[1] 李建林.風力發電系統低電壓運行技術[M].北京: 機械工業出版社,2009: 67-69.

[2] 樂江源,謝運祥,洪慶祖,等.Boost 變換器精確反饋線性化滑模變結構控制[J].中國電機工程學報,2011,31(30): 16-23.

[3] 孫永清,張超,翟俊峰,等.永磁同步風力發電系統最大功率跟蹤控制策略及仿真分析[J].水電能源科學,2012,30(9): 192-194,157.

[4] Savaresi S M.Exact Feedback Linearization of Fifth Order Model Synchronous Generators[C].IEEE proceedings.Control theory and applications.1999,146(1): 53-57.

[5] 陳思哲,吳捷,姚國興,等.基于微分幾何的風力發電機組恒功率控制[J].控制理論與應用,2008,25(2): 336-340.

[6] Cutululis N A,Ceanga E,Hansen A D.Robust multi- model control of an autonomous wind power system[J].Wind Energy,2006,9(5): 399-419.

[7] 王利兵,毛承雄,陸繼明,等.基于反饋線性化原理的直驅風力發電機組控制系統設計[J].電工技術學報,2011,26(7): 1-6,20.

[8] Nicolas Antonio Cutululis.Feedback linearization control of wind power system 2004 ISSN 1221-454X.

[9] Hassan K K.Nonlinear systems[M].Third Edition.New Jersey,USA: Prentice Hall,2002: 430-438.

[10] 耿華,許德偉,吳斌,等.永磁直驅變速風電系統的控制及穩定性分析[J].中國電機工程學報,2009,29(33): 68-75.

[11] Carr J.Application of center manifold theory[M].NewYork: Springer-VerlagBerlin: Heidelberg,1981.

[12] 盧強,孫元章.電力系統非線性控制[M].北京: 科學出版社,1993: 94-99.

[13] Li Zhong,Zhang Bo.Bifurcation analysis of the Permanent-Magnet synchronous motor models basedon the center manifol theorem[J].Control Theory and Applications,2000,17(3): 317-320.

[14] 劉金琨.滑模變結構控制Matlab 仿真[M].2 版.北京 : 清華大學出版社,2008: 83-87.