高超聲速飛行器主動式氣膜冷卻防熱技術研究

向樹紅，張敏捷，童靖宇，李海波，朱云飛，楊艷靜，崔麗娟

（1.北京衛星環境工程研究所，北京 100094；2.可靠性與環境工程技術重點實驗室，北京 100094）

高超聲速飛行器一般是指飛行馬赫數大于5、能在大氣層和跨大氣層中遠程飛行的飛行器，其應用形式包括高超聲速有人/無人飛機、空天飛機和返回式航天器等多種飛行器。高超聲速飛行器在今后相當長的時間里將是航空航天技術發展的最前沿。另一方面，高超聲速飛行器面臨的“熱障”、“黑障”（等離子體）和“氣動光學”效應是世界性的難題[1—2]。當飛行速度達到20 Ma，高超聲速飛行器激波后的氣流溫度可達約10 000 K（接近太陽表面溫度的1.5倍）。飛行器以高馬赫數巡航時間長達1000 s，這給飛行器自身的材料和結構都提出了極高的熱防護要求。目前采用較多的幾種防熱手段防熱能力有限，并且都不同程度地增加了飛行器質量，同時也使飛行器表面氣動結構復雜化。另外，受金屬殼體和內部元件使用溫度（最高不超過150℃）、彈徑尺寸等多方限制，現有的被動熱防護（防熱瓦、碳碳材料、碳硅材料）均已無法完成下一步型號研制的需求。

氣膜冷卻作為一種有效的主動冷卻方式已被廣泛地應用于航空燃氣渦輪發動機渦輪葉片上，成為航空燃氣渦輪發動機高溫部件的主要冷卻措施之一，其技術應用已非常成熟[3]。研究氣膜冷卻的相關文獻已近萬篇。氣膜冷卻流動結構復雜，影響因素眾多。如何通過優化氣膜冷卻結構及射流參數，實現使用相對少的冷卻氣體量來獲得相對高的冷卻效果（低熱流密度），是值得不斷探索的研究課題。

超聲速流動與亞聲速流動本質不同，而高超聲速流動更加復雜：激波層很薄，與邊界層產生黏性干擾，高溫空氣導致強烈的化學反應及電離效應，而射流又會使得流動結構更加復雜。因此，針對高超聲速飛行器的氣膜冷卻的研究極為困難，不能簡單地將低速氣膜冷卻中已有的結論照搬過來。

目前針對高超聲速飛行器的氣膜防熱的研究不多，所針對的來流速度不超過10 Ma[4—6]。為了減小計算難度，氣膜孔多分布在非駐點區域[7]（這恰恰是舍本逐末的，因為飛行器熱環境最嚴苛區域為頭駐點區域）。氣膜孔為簡單的圓柱直孔[8]，冷卻效率相比異型孔較低。

筆者針對未來高超聲速飛行器，提出了一種主動式氣膜冷卻防熱技術，并采用數值模擬手段（CFD），計算了高超飛行器的氣膜冷卻效率，驗證了氣膜冷卻技術應用于高超聲速飛行器的可行性。

1 理論基礎

高超聲速飛行器在大氣層飛行時，氣流受到頭部的強烈壓縮，會在頭部形成弓形脫體激波。在此飛行條件下，飛行器大量動能耗散，轉化為熱能，使得飛行器周圍流體產生很高的溫度，本體周圍的氣體也由于黏性阻滯作用，產生嚴重的氣動加熱，從而形成高溫高焓流場。此時流場內部區域多組元氣體將發生分子振動能量激發、離解、電離、復合和光化學反應等一系列復雜的物理化學過程。這些現象會影響氣體熱力學特性，使得氣體偏離完全氣體的特性。

1.1 高超聲速黏性流動控制方程

直角坐標系下，包含化學反應源項的三維守恒型Navier-Stokes方程組如下[9]：

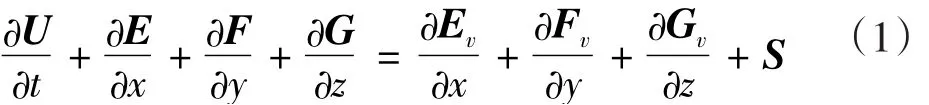
式中：U為守恒狀態變量向量；E，F，G為對流項向量；Ev，Fv與Gv為黏性項向量；S為化學反應源項。

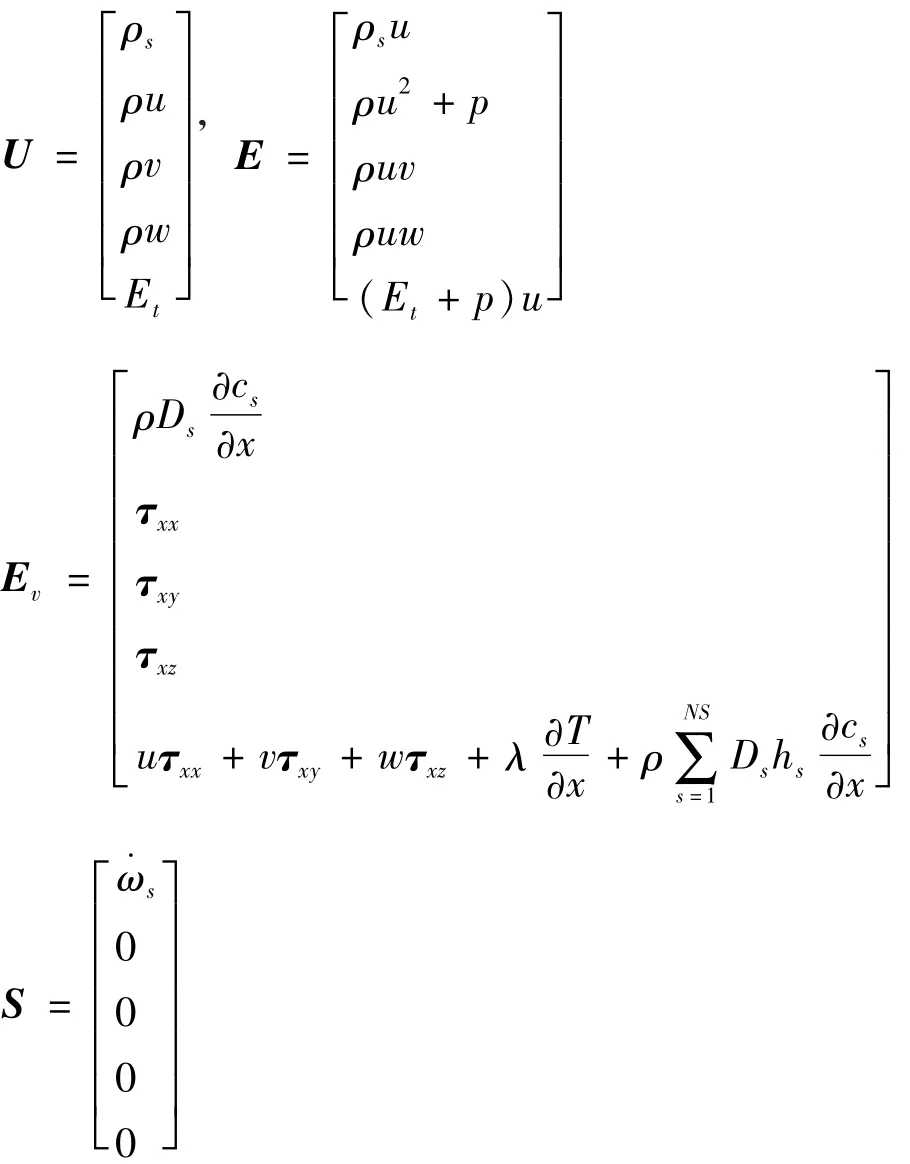
F，G與E表達式相似；Fv，Gv與Ev表達式相似。其中：p，ρ，T分別為混合氣體壓強、密度及溫度；，hs，cs，Ds為氣體各組分密度、焓、質量分數、擴散系數；u，ν，w為氣體速度分量；Et為單位體積氣體總能量；，等為應力張量。

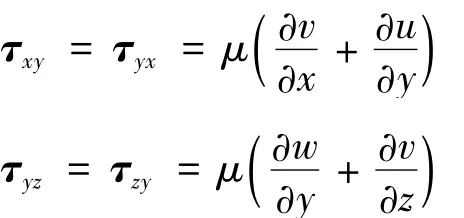
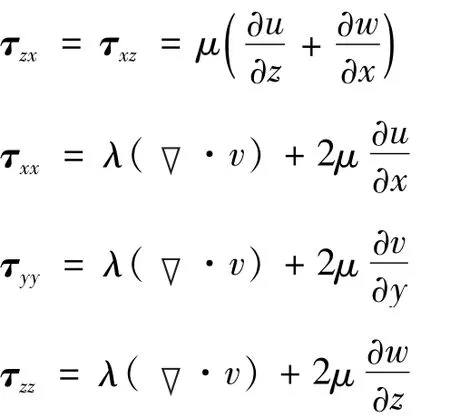
1.2 化學反應機理

1.2.1 基元反應

一個化學反應的發生一般由多步基元反應組成。基元反應定義為由反應物一步生成相應產物的化學反應。假設文中研究的化學反應由K個基元反應組成，代表第s個組元，則系統總體化學反應方程式可以寫為：

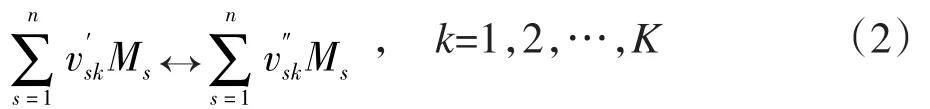
1.2.2 化學反應速率

前向化學反應速率由Arrhenius公式求出，反應速率是溫度的函數，逆向反應速率采用平衡常數求出：

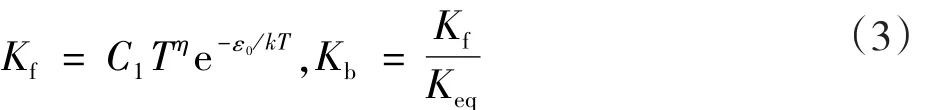
C1，η和為通過實驗數據擬合出來的系數。該化學反應還包括一個第三體（M）及其效率。第三體又可稱為碰撞體，起能量傳遞作用。

文中化學反應采用PARK-I的5組分17步反應模型[10]。PARK-I模型是用來模擬不考慮電離的空氣離解反應的通用格式之一，包括5種組分（N2，O2，N，O，NO）、17步基元反應，化學反應速率遵守Arrhenius公式。具體參數見表1。

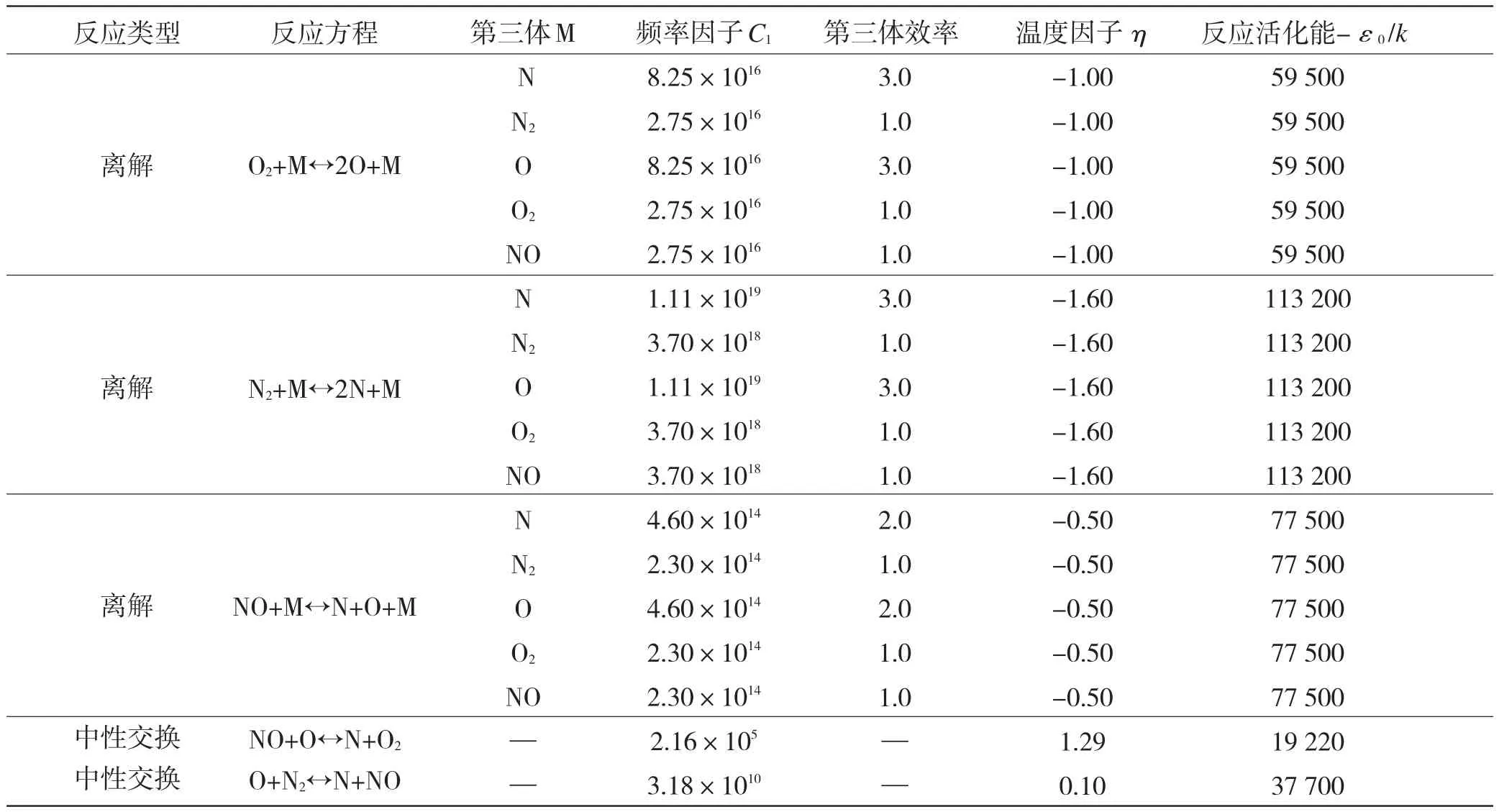
表1 Park-1化學反應模型Table 1 Park-1 reaction scheme for air

2 CFD計算程序驗證

為驗證CFD程序的正確性，選取NASA TN D-5450報告[11]中的實驗模型，利用CFD程序進行仿真計算。此報告對球頭錐進行了詳細研究和大量試驗，試驗數據可靠。

2.1 計算模型

計算模型為如圖1所示的球頭錐模型。

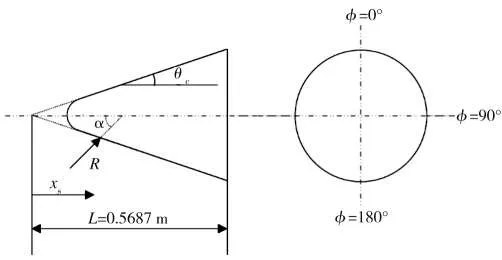
圖1 幾何模型-球頭錐Fig.1 Geometry model-cone

模型半錐角θc=15°。取實驗中的4個典型工況（Case 1，2 ，3，4），各工況中來流馬赫數Ma∞=10.6，速度 v=1461.92 m/s，溫度 T∞=47.34 K，壁面溫度 Tw=294.44 K。Case1/2幾何模型頭部半徑為0.008 525 m，自由來流壓強為132.06 Pa，Case 3/4幾何模型頭部半徑為0.027 94 m，自由來流壓強為198.09 Pa。Case 1/3攻角為0°，Case 2/4攻角為20°。

為節省計算資源，取模型的一半進行計算。利用ICEM劃分結構網格，在近壁面處對網格進行了適當的加密，近壁面法向第一層網格高度為0.001 mm。網格數量分別為702 108個（Case1/2）和458 370個（Case3/4）。

根據實驗條件，使用層流模型進行計算。通量分裂格式使用Van Leer′s FVS格式，通量限制器為Osher-C（L）。

2.2 計算結果

Case 3中溫度云圖和頭部附近等壓強線如圖2所示。

圖2 Case 3流場溫度云圖和壓強等值線圖Fig.2 Contour of field temperature and pressure for case 3

四種工況下壁面熱流密度計算結果與實驗數據的對比如圖3所示。整體來看，計算結果與實驗數據吻合得非常好；個別情況下，當計算帶有攻角的工況（Case 2/4）時，迎風面計算結果略微偏低。這可能是由于有攻角時迎風面流動出現分離，而層流模型導致計算結果略微偏低。

圖3 計算結果與實驗數據對比Fig.3 Comparison between CFD results and experimental data

3 氣膜冷卻

高超聲速飛行器面臨的熱力環境極其惡劣，現有的熱防護技術防護能力有限，難以滿足未來高超聲速飛行器（20 Ma）的防熱要求（可承受極高熱流密度、持續較長時間、可重復使用），目前針對高超聲速飛行器防熱系統的設計思想及發展趨勢是從全部被動式防熱逐步走向在局部高溫區采用主動防熱技術。為此，將航空發動機中廣泛應用的主動式氣膜冷卻技術應用到高超聲速飛行器防熱中。

3.1 計算條件

首先計算無氣膜冷卻時的流場。由于考慮真實氣體效應時計算量非常大，為盡量減少計算資源的消耗，節省計算時間，同時保證計算精度，截取球頭錐前半部分長為0.10 m的部分重新劃分流場網格進行計算，并在初步計算的基礎上將流場區域劃分得盡量小，所得最終網格數量為105 612；在壁面附近對網格進行加密，近壁面法向第一層網格高度為0.002 mm。

式中：μX和 μY分別表示圖像X和Y的均值；σX和 σY分別表示X和Y的方差；σXY表示X和Y的協方差；C1和C2為常數。

然后計算單孔氣膜冷卻時的流場。計算主體幾何外形與第二章中所述相同，不同的是在球頭駐點處構造入口直徑2 mm、長10 mm的漸擴異型孔，向外噴射冷卻工質（空氣）。具體幾何尺寸如圖4所示。

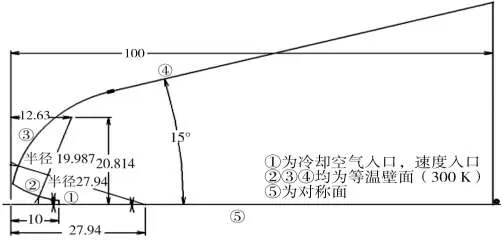
圖4 氣膜孔幾何尺寸（mm）Fig.4 Geometry of the hole（mm）

為了精確捕捉射流孔附近的流動特征，在射流孔附近及近壁面處對網格進行手動加密，近壁面法向第一層網格高度為0.002 mm，最終網格數量為776 556，如圖5所示。

圖5 氣膜孔附近網格Fig.5 CFD grid of the hole

計算的自由來流條件為20 Ma，取30 km高度處的大氣值，壓強P∞=1185.5 Pa，溫度T∞=231.24 K。射流入口使用速度入口邊界條件：保持總壓和總溫不變，入口靜壓3 MPa，入口速度200 m/s（當地馬赫數約為1），溫度壁面為等溫壁面（300 K）。湍流模型為Menter SST模型[12]。該湍流模型結合了k-ε模型和k-ω模型，在近壁面處采用k-ω模型，遠離壁面處采用k-ε模型，避免了k-ω湍流模型對于自由來流湍流度的敏感性，同時，對逆壓梯度和分離流動模擬的效果較好。化學反應模型采用PARK 5組分（N2，O2，N，O，NO）17反應方程化學模型。

3.2 計算結果

經過反復迭代后計算，計算結果趨于穩定。收斂準則為10-3，監測點的各變量（密度，速度，溫度）無變化，計算結果收斂。

由圖6可以看出：隨著流動速度的增大，激波后氣體溫度急劇升高，馬赫數為20時可達9827 K，約為太陽表面溫度（6000 K）的1.5倍；化學反應效應非常明顯，O原子質量分數最高可達25.17%，氧氣分子全部離解。值得一提的是，由于使用Roe通量格式，計算結果出現了所謂的“紅玉”現象（carburetor）[13]，關于這個問題的討論不屬于文中所研究的范圍。

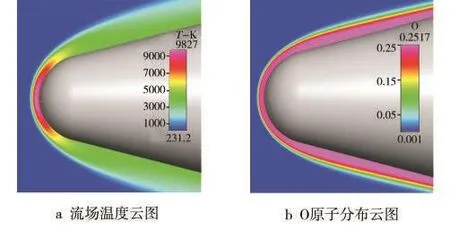
圖6 Ma=20無氣膜冷卻時流場溫度及O原子質量分數云圖Fig.6 Contour of field temperature and mass fraction of O atom at Mach 20 without film cooling

圖7 為有射流時流場溫度云圖。射流流場結構非常復雜。由于在噴口附近的膨脹波的過度膨脹，在射流出口處形成懸掛的馬赫盤。射流通過馬赫盤后與主流接觸，形成弓形激波。由于射流的作用，弓形激波扭曲變形并遠離鈍體頭部，射流在主流的作用下又附著在物體表面上，剪切作用在噴口附近形成低壓回流區。由于冷卻氣流與主流的摻混換熱作用，主流最高溫度下降到7047 K。孔口附近的流場包含了激波、馬赫盤、剪切層、回流區、激波-激波干擾、激波邊界層干擾等流動現象。數值模擬結果精確捕捉了氣膜冷卻射流流場結構，也與低馬赫數下氣膜冷卻的規律一致[14—17]。

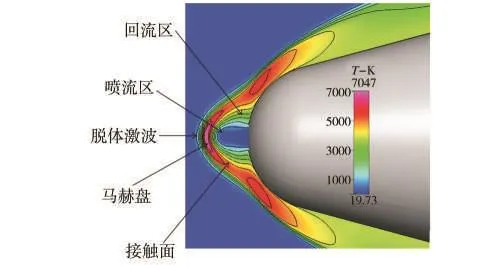
圖7 有氣膜冷卻時流場溫度云圖Fig.7 Contour of field temperature with film cooling

圖8a為O原子分布云圖，在孔口附近相當大的區域內，氣流溫度較低，導致氧氣分子未離解，O原子含量較低。圖8b為射流孔附近速度矢量圖，壁面為熱流密度分布云圖，可清晰地看出孔口附近的渦系結構。單個氣膜孔有效冷卻覆蓋面積約為出口孔面積的10倍。

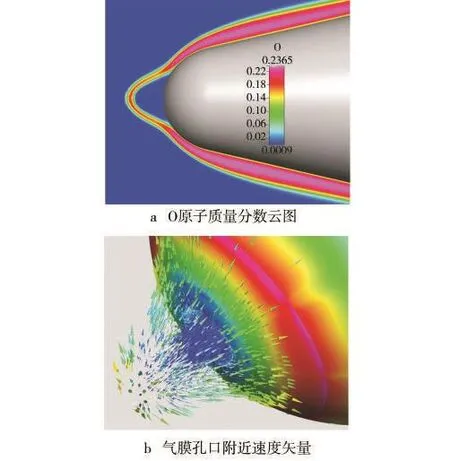
圖8 有氣膜冷卻時O原子質量分數云圖及氣膜孔口附近速度矢量Fig.8 Contour of fraction of O with film cooling and vector plot of the flow in the vicinity of the hole

圖9 有氣膜冷卻和無氣膜冷卻時壁面熱流密度分布Fig.9 Comparison of heat flux distribution on the wall with and without film cooling

另一方面，可以想象，若在熱流密度最大值處再加上一個射流孔，壁面熱流密度將進一步降低，這也為后續研究提供了思路。

4 結語

文中針對未來高超聲速飛行器，提出了一種主動式氣膜防熱技術，并從計算流體力學的角度，研究了單個異型孔的氣膜冷卻效果。結果表明，對于高超聲速飛行器，氣膜冷卻效果較好，主動式氣膜冷卻技術具有非常廣闊的應用前景。

已有的關于低速氣膜冷卻的研究表明，影響氣膜冷卻效果的因素眾多，包括單個氣膜孔的幾何結構（氣膜孔形狀及孔長度、孔徑等）、氣膜孔的噴射角度（包括流向傾角即冷氣流出射方向與被冷卻壁面切向的夾角和側向傾角）、氣膜孔排列方式（孔間距、孔排距、孔排數、孔的排列方式）、氣膜射流參數及主流參數（主流速度、吹風比、射流與主流的密度比、動量比、噴射壓力損失、壓力梯度、主流湍流度和氣膜孔上游的主流邊界層厚度等）及其他影響參數（冷卻工質、壁面形狀、表面曲率、表面粗糙度等）。另一方面，對于主動冷卻，還應考慮熱應力、斷裂剛度、冷卻劑、工藝（無泄漏、無通道堵塞）、系統的相容性等。設計和制造主動冷卻結構存在一定的困難，因為從表面到冷卻通道之間存在劇烈的溫度變化使得熱應力很大，同時冷卻劑需要很高的運行壓力。主動冷卻結構還要解決許多設計、工藝和使用問題，包括提高防止產生故障的能力、驗證有無泄漏和保證輕質冷卻系統的壽命（包括重新填裝冷卻劑和維持壓力等）。

進一步的工作可在如下幾個方面進行。

1）首先對單孔射流進行優化設計，調整射流出口壓力、速度，尋找最佳射流參數；對射流孔的形狀進行優化設計，提高冷卻效率。

2）對多孔射流進行研究，研究射流相互之間的影響；通過在壁面合適的位置布置經過特殊設計的射流異型孔，使得冷卻氣流均勻覆蓋整個飛行器表面，從而達到較為理想的熱防護效果。

3）對氣膜冷卻結構性能進行分析設計，使得布置氣膜孔后，結構滿足強度要求。

4）結合飛行器結構尺寸限制以及流體力學、結構強度設計、工藝等要求，對氣膜冷卻進行系統綜合設計，形成了一套工程上可行的、適用于高超聲速飛行器的氣膜冷卻系統。

對于高超聲速飛行器氣膜冷卻技術，還需做大量的研究工作。這項技術一旦發展成熟并付諸工程應用，能使得高超聲速飛行器技術取得突破性進展。

[1] 向樹紅，榮克林，黃訊，等.航天產品環境試驗技術體系現狀分析與發展建議[J].航天器環境工程，2013，30（3）：269—274.XIANG Shu-hong，RONG Ke-lin，HUANG Xun，et al.The Technical System of Environmental Tests for Spacecraft Products[J].Spacecraft Environment Engineering，2013，30（3）：269—274.

[2] 童靖宇，向樹紅.臨近空間環境及環境試驗[J].裝備環境工程，2012，9（3）：1—4.TONG Jing-yu，XIANG Shu-hong.Near Space Environment and Environment Tests[J].Equipment Environmental Engineering，2012，9（3）：1—4.

[3] BUNKER R S.A Review of Shaped Hole Turbine Film-cooling Technology[J].Journal of Heat Transfer，2005，127：441—453.

[4]PUDSEY A S，BOYCE R R，WHEATLEY V.Hypersonic Viscous Drag Reduction via Multiporthole Injector Arrays[J].Journal of Propulsion and Power，2013，29（5）：1087—1096.

[5]HEUFER K A，OLIVIER H.Film Cooling of an Inclined Flat Plate in Hypersonic Flow[C]//14th AIAA/AHI Space Planes and Hypersonic Systemsand TechnologiesConference.Amerca：AIAA，2006：8067.

[6]HEUFER K A，OLIVIER H.Experimental and Numerical Study of Cooling Gas Injection in Laminar Supersonic Flow[J].AIAA JOURNAL，2008，46（11）：2741—2751.

[7]KIM S I，HASSAN I.Numerical Study of Film Cooling Scheme on a Blunt-nosed Body in Hypersonic Flow[J].Journal of Thermal Science and Engineering Applications，2011，3（044501）：1—7.

[8]JOSEPH J，SHINE S R.Coolant Gas Injection on a Blunt-nosed Re-entry Vehicle[C]//Proceedings of the ASME 2013 Gas Turbine India Conference.India，2013.

[9]ANDERSON J D.Hypersonic and High-temperature Gas Dynamics[M].America：AIAA Education Series，2006.

[10]PARK C.On Convergence of Computation of Chemically Reacting Flows[C]//23rd AIAA Aerospace Sciences Meeting.America：AIAA，1985.

[11]CLEARY J W.Effects of Angle of Attack and Bluntness on Laminar Heating-rate Distributions of a Cone at a Mach Number of 10.6，Nasa tnd-5450[R].1969.

[12]MENTER F R.Two-equation Eddy-viscosity Turbulence Models for Engineering Applications[J].AIAA Journal，1994，32（8）：1598—1605.

[13]QUIRK J.A Contribution to the Great Riemann Solver Debate[R].Speringfield：NASA Langley Research Center，1992.

[14]MEYER B，NELSON H F.RIGGINS D W.Hypersonic Drag and Heat-transfer Reduction Using a Forward-facing Jet[J].Journal of Aircraft，2001，38（4）：680—686.

[15]RONG Yi-sheng.Reduction Research in Supersonic Flow With Opposing Jet[J].Acta Astronautica，2013，91：1—7.

[16]HAYASHI K,ASO S，TANI Y.Experimental Study on Thermal Protection System by Opposing Jet in Supersonic Flow[J].Journal of Spacecraft and Rockets，2006，43（1）：233—235.

[17]何琨，陳堅強，董維中.逆向噴流流場模態分析及減阻特性研究[J].力學學報，2006，38（4）：438—445.HE Kun，CHEN Jian-qiang，DONG Wei-zhong.Penetration Mode and Drag Reduction Research in Hypersonic Flows Using a Counter Flow Jet[J].Chinese Journal of Theoretical and Applied Mechanics，2006，38（4）：438—445.