敏感器的步降應力加速壽命試驗方法研究

王紹山，宣兆龍，王耀冬，王維

（軍械工程學院，石家莊 050003）

敏感器作為智能彈藥的重要組成部分，對儲存環境比較敏感，是彈藥儲存過程中的短板，其儲存壽命長短直接決定智能彈藥的儲存可靠性和儲存年限。由于敏感器中存在著大量易損的光電器件，其儲存壽命的不確定性增加了彈藥倉庫管理的難度，因此如何對敏感器的儲存可靠性進行評估成為研究人員關注的焦點。文中以敏感器為研究對象，在分析敏感器特點的基礎上，提出采用步降應力加速壽命試驗對敏感器進行試驗，并利用最優線性無偏估計方法進行了分析。

1 敏感器

敏感器是智能彈藥的核心關重件之一，主要用來完成對目標的探測、識別等功能。敏感器按照電磁波探測的方式可以分為有源和無源兩種：有源探測器特指各波段的雷達，利用其散射截面來提供彈與目標的距離；無源探測器特指輻射計，測量目標與其背景間的輻射功率差異[1]。敏感器具有以下特點[2]：探測時停留時間較短，對本身有較高的方向性要求。適應能力較強，能在多種環境條件下工作。探測距離較近，一般在幾十米到幾百米之間。結構復雜，儲存環境要求高。

以末敏彈為例，美國、俄羅斯、法國、德國和瑞典等國家從20世紀70年代開始研制末敏彈。其敏感器由剛開始的單一敏感體制發展到現在的復合敏感體制，集紅外敏感器、毫米波雷達、毫米波輻射計和激光雷達等功能于一體，各探測器優勢互補，使其在復雜環境中能夠保證完成探測識別。

目前，世界上具有代表性的末敏彈中利用的敏感器探測識別系統見表1。

表1 末敏彈載敏感器配置Table 1 Configuration of sensors in each terminal-sensitive projectile

2 敏感器的可靠性評估方法

敏感器儲存壽命的長短對部隊來說至關重要，進行可靠性評估能夠使彈藥倉庫人員明確其儲存可靠性和儲存年限。文中采用步降應力加速壽命試驗對敏感器進行試驗，檢驗其可靠性。

2.1 步降應力加速壽命試驗

步降應力加速壽命試驗是通過對樣本加載應力水平步降減小的加速應力來進行試驗，進而分析得到樣本壽命統計特征的加速壽命試驗方法[3]。試驗時，對樣品首先進行高應力水平試驗，在到達設定的條件（定時或定數）后，將應力下降到下一水平，直到達到規定條件。其應力加載的過程如圖1所示。

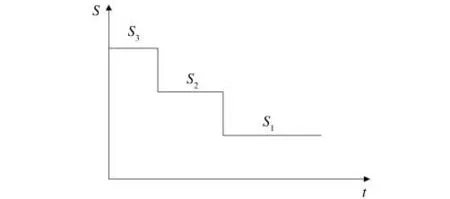
圖1 步降應力加速壽命試驗應力加載Fig.1 Stress of step-down-stress accelerated life test

1980年，Nelson在試驗的基礎上提出了著名的“累積失效模型”，即產品的殘存壽命僅依賴于已經累積的失效概率和當前的應力水平，與累積方式無關[4]。步降應力加速壽命試驗將最高應力放在前面，要達到相應的失效概率需要的時間大大縮短。

2.2 敏感器的步降應力加速壽命試驗

由于各敏感器中有著大量的光電探測器件，所以根據實際經驗，其壽命服從威布爾分布，其分布函數為：

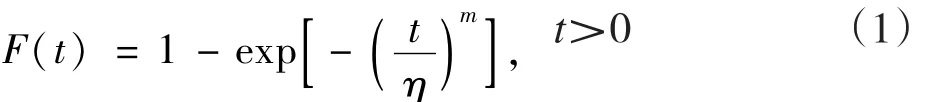
式中：m為形狀參數；η為特征壽命[5]。

結合敏感器的實際情況，步降應力加速壽命試驗中部分試驗參數，如應力模型、截尾方式、應力水平、試驗時間等可基本確定。

2.2.1 應力模型

在加速壽命試驗中，有3種最常用的應力模型，即Arrhenius模型、逆冪律模型和Eyring模型。由于敏感器中存在大量的電子元器件，因此，在選擇溫度作為加速應力時，應當選取Arrhenius模型。

Arrhenius模型主要是以溫度作為加速試驗應力，能加快元件特別是電子元器件內部反應，促使其失效。該模型表達式為：

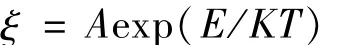
式中：ξ為產品的某個壽命特征；A為常數；E為激活能，與材料有關；K為波爾茲曼常數；T為絕對溫度。

將Arrhenius模型兩邊取對數后，可得：

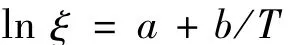
式中：a=ln A，b=E/K。這表明產品某個壽命特征的對數與溫度的倒數是線性關系，簡化了試驗后的數據處理。在此次試驗中，選取ξ為η。即：

2.2.2 截尾方式

在加速壽命試驗中，截尾方式有定時和定數截尾兩種。如果使用定數截尾，那么在試驗過程中需要進行連續、實時檢測[6]，這加大了試驗量。另外，敏感器作為高價值彈藥的一部分，其失效個數會較少，甚至會出現零失效，因此，在試驗時應當選取定時截尾方式。為了不使失效個數過少或過多，恰當的規定試驗的截止時間是成功實施定時截尾試驗的關鍵[3]。

2.2.3 加速應力水平的確定

試驗選取的應力水平越多，則試驗后的分析精度越高，但是試驗的樣本量和成本也會增加。鑒于某型敏感器造價昂貴，不可能有大量樣品進行試驗，同時，在國標中對試驗應力水平也做出了相關的建議，所以，平衡之下選取4個應力水平（S4，S3，S2和S1）。最高應力水平不能超過敏感器的極限應力，一般低于極限應力3～5℃，應力與應力間隔為5～10℃。

2.2.4 步降應力試驗時間的確定

根據國軍標對步加試驗時間的確定方法，步加試驗總時間是貯存壽命值的1/20至1/40[7]。文獻[4]和[8]中指出，在保證相同試驗信息量的前提下，步降應力試驗的總試驗時間是步進應力試驗總時間的30.7%。因此，步降應力試驗總時間可以選擇為貯存壽命值的1.535%～0.7675%。步降應力試驗各應力水平下試驗時間分別為總時間的1/10，2/10，3/10，4/10，當第一個應力水平下無失效樣品出現時，則延長第一個應力的試驗時間，直到出現失效為止。其他應力水平試驗時間也相應的延長，分別是第一應力水平時間的2倍、3倍和4倍。

2.2.5 加速系數的確定

加速系數是指正常應力下某種特征壽命與加速應力相應壽命特征的比值[9]。敏感器在服從威布爾分布條件下，其特征壽命η一般選取其p分位壽命（此處p=1-e-1=0.632）。因此，兩個加速應力之間的加速系數為：

2.3 試驗數據的處理

對壽命服從威布爾分布的元器件的試驗數據進行處理，確定相關參數時，比較經典的方法是極大似然估計法和逆矩估計法。由于極大似然估計在計算時較為復雜，所以選擇逆矩估計法[10]。

2.3.1 數據的折算

由式（1）可知，服從威布爾分布的敏感器壽命的密度函數是：

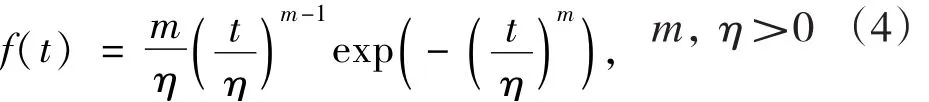
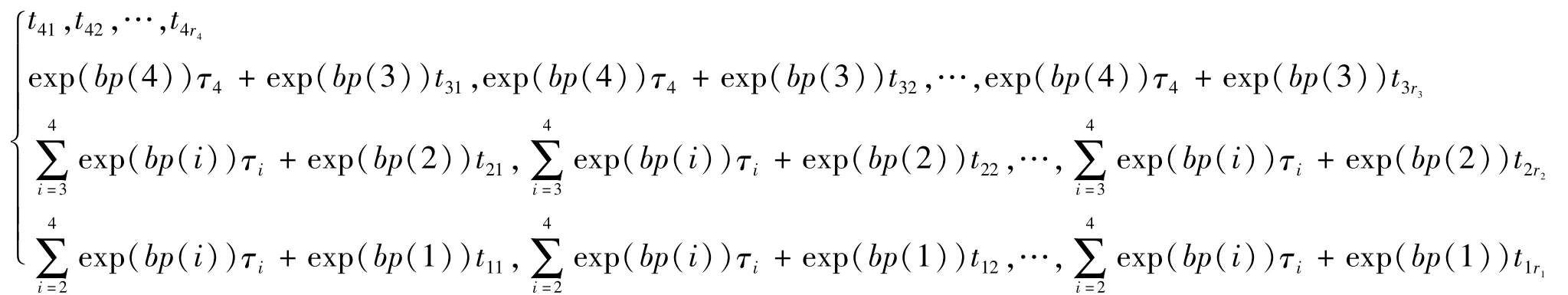
記以上數據分別為t1（b）＜t2（b）＜…＜tr（b）。

2.3.2 參數的求值

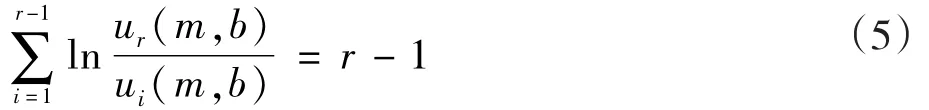
式（5）中含有兩個未知數即m和b。因此，可再利用最優線性無偏估計增加一個關于m和b的關系式[12]：

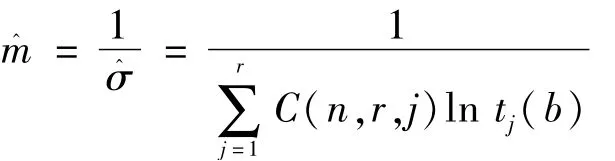
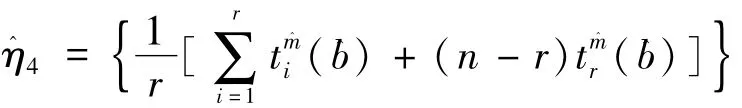
3 結語

文中以敏感器作為研究對象，分析了其步降應力加速壽命試驗所需的各項參數，利用三步分析法[15]對數據進行處理，即數據折算，分布參數估計和加速模型回歸分析。分析結果表明，利用逆矩估計法可以估計出樣品的可靠性參數，為步降應力加速壽命試驗的具體實施奠定了基礎。

[1] 楊紹卿.靈巧彈藥工程[M].北京：國防工業出版社，2010.YANG Shao-qing.Smart Munition Engineering[M].Beijing：National Defense Industry Press，2010.

[2]程澤.基于小子樣理論的某型末敏彈鑒定試驗方法研究[D].石家莊：軍械工程學院，2013.CHENG Ze.Research on Evaluation Test of a Terminal-Sensitive Projectile Based on Small Sample Statistic Theory[D].Shijiazhuang：Ordnance Engineering College，2013.

[3] 張春華.步降應力加速壽命試驗的理論和方法[D].長沙：國防科技大學，2002.ZHANG Chun-hua.Theory and Method of Step-down-stress Accelerated Life Testing[D].Changsha：National University of Defense Technology，2002.

[4]NELSON W.Accelerated Life Testing-step-stress Models and Data Analysis[J].IEEE Trans on Reliability，1980，29（2）：103—108.

[5] 茆詩松，王玲玲.加速壽命試驗[M].北京：科學出版社，1997.MAO Shi-song，WANG Ling-ling.Accelerated Life Test[M].Beijing：Science Press，1997.

[6] 宣兆龍，程澤，劉亞超.紅外敏感器加速壽命試驗方法研究[J].裝備環境工程，2012，9（6）：44—50.XUAN Zhao-long，CHENG Ze，LIU Ya-chao.On Accelerated Life Test Method of High-power Infrared Sensor[J].Equipment Environmental Engineering，2012，9（6）：44—50.

[7]GJB5103—2004，彈藥元件加速壽命試驗方法[S].GJB5103—2004，Accelerated Life Test Method for Ammunition Components[S].

[8] 陳循，張春華，汪亞順，等.加速壽命試驗技術與應用[M].北京：國防工業出版社，2013.CHEN Xun，ZHANG Chun-hua，WANG Ya-shun，et al.Accelerated Life Testing Technology and Application[M].Beijing：National Defense Industry Press，2013.

[9] 丁孝均，趙光輝，趙云峰，等.橡膠密封材料加速系數研究[J].宇航材料工藝，2013，1：93—97.DING Xiao-jun，ZHAO Guang-hui，ZHAO Yun-feng，et al.Investigation on the Accelerated Factor of Rubber Sealing Materials[J].Aerospace Materials&Technology，2013，1：93—97.

[10]王炳興.Weibull分布基于恒加壽命試驗數據的統計分析[J].應用概率統計，2002，18（4）：413—418.WANG Bing-xing.Statistical Analysis for the Weibull Distribution Based on Constant Stress Accelerated Life Test Data[J].Chinese Journal of Applied Probability and Statisties，2002，18（4）：413—418.

[11]明志茂，陶俊勇，陳循，等.動態分布參數的貝葉斯可靠性分析[M].北京：國防工業出版社，2011.MING Zhi-mao，TAO Jun-yong，CHEN Xun，et al.Bayes Reliability Analysis of Dynamic Distribution Parameter[M].Beijing：National Defense Industry Press，2011.

[12]張志華.加速壽命試驗及其統計分析[M].北京：北京工業大學出版社，2002.ZHANG Zhi-hua.Accelerated Life Test and Its Statistical Analysis[M].Beijing：Beijing University of Technology Press，2002.

[13]張春華，溫熙森，陳循.加速壽命試驗技術綜述[J].兵工學報，2004，25（4）：485—490.ZHANG Chun-hua，WEN Xi-sen，CHEN Xun.A Comprehensive Review of Accelerated Life Testing[J].Acta Armamentarii，2004，25（4）：485—490.

[14]李海波，張正平，胡彥平.加速壽命試驗方法及其在航天產品中的應用[J].強度與環境，2007，34（1）：2—10.LI Hai-bo，ZHANG Zheng-ping，HU Yan-ping.Accelerated Life Testing Method and Its Applications for Space Products[J].Structure&Environment Engineering，2007，34（1）：2—10.

[15]張春華，陳循，溫熙森.步降應力加速壽命試驗（下篇）——統計分析篇[J].兵工學報，2005，26（5）：666—669.ZHANG Chun-hua，CHEN Xun，WEN Xi-sen.Step-downstress Accelerated Life Testing-Statistical Analysis[J].Acta Armamentarii，2005，26（5）：666—669.