一種改進的BM算法性能分析

朱保鋒，宋 艷

(河南教育學院信息技術系，鄭州 450046)

隨著計算機應用技術的快速發展，處理非數值數據的應用增長迅速，使得字符匹配問題顯得尤為重要，在入侵檢測、信息檢索、搜索引擎等領域都有所涉及，字符匹配算法效率的高低對搜索引擎在數據查找方面的性能有著非常直接的影響。因此需要找到一種適合、高效的字符匹配算法。

1 BM算法概述

字符匹配是將搜集到的文本信息和數據庫中已經存在的模式數據信息進行比較，找出模式串在文本串中的出現位置。當前的字符匹配算法有很多種，例如:蠻力算法、BM 算法、Horspool算法、Wu-Manber算法等。基于字符掃描策略的不同，字符匹配算法可以分為三類:1)從左到右掃描模式和文本每一對相應的字符，一旦不匹配，模式右移一格，進行下一輪嘗試，蠻力字符匹配就是該類算法，其平均效率是屬于O(n*m)的。2)自右向左匹配文本串與模式串的最大后綴，BM算法、Horspool算法屬于此類，BM的最差效率是線性的，Horspool是BM的簡化版本。3)自右向左匹配文本串與模式串的最大子串。

1977年，Robert S.Boyer和 J Strother Moore提出了另一種在O(n)時間復雜度內，完成字符串匹配的算法，其在絕大多數場合的性能表現，比KMP算法還要出色，這就是BM算法，一直被認為是最有效的字符匹配算法，開源入侵檢測系統Snort就是采用BM算法［1］。但是在BM算法中，有些比較是多余的，降低了算法的執行效率，因此提出一種改進的BM算法，通過實驗數據可以表明，改進后的算法能夠提高傳統BM算法的效率。

2 BM算法的基本原理

BM算法被認為是亞線性串匹配算法，它在最壞情況下找到模式所有出現的時間復雜度為O(mn)，在最好情況下執行匹配找到模式所有出現的時間復雜度為O(n/m)。

2.1 定義

定義1:設Σ為字母表，T，P∈Σ+，其中文本串T=t0t1t2…tn-1，模式串 P=p0p1p2…pm-1，m ＜ n。

定義2:c∈Σ且c∈T，c是壞符號，導致模式串P和字符串T的相應字符不匹配;d是模式串相對于文本串移動的距離;k∈N，是文本串與模式串匹配的最大后綴。

2.2 BM算法的工作原理

文本串T與模式串P左對齊，從pm-1開始自右向左，比較文本和模式的相應字符對，如果p0p1p2…pm-1與T中的 titi+1ti+2…ti+m-1一一匹配，則找到了P在T中的出現，返回i，如果模式P超出了文本T，則P沒有在T中出現，返回 -1。

模式串P最右邊的字符pm-1和文本串T的相應字符c初次比較失敗了，模式串P要盡量向右移動足夠長的距離［2］，以減少移動的次數和比較的次數，降低算法的復雜度。如果c不包含在P的前m-1個字符中，P移動的最長距離為len(P)=m;如果c出現在P的前m-1個字符中(出現的次數有可能＞1)，此時向右移動P，使P中最右邊的c和T中的c對齊，此時P的移動距離是和c相關的。將模式P向右移動的長度用t(c)表示為［3］:

模式串P與文本串T在遇到壞符號c之前，已經有k(0＜k＜m)個字符成功匹配，模式串P向右移動的長度d參照兩個規則:壞符號移動規則和好后綴移動規則。

壞符號移動規則:該規則參照壞符號c，如果c不在P中，將P移動到正好跳過字符c，移動的長度表示為m-k;如果c存在于模式中，將P前m-k個字符最右邊的c和T中的c對齊，參照公式(1)，P移動的距離表示為t(c)-k。當k相對于t(c)足夠大時會導致t(c)-k＜0，參照蠻力算法可以使P向右移動1個位置。針對字母集Σ中的每個字符計算壞符號移動表，壞符號移動的距離表示為:

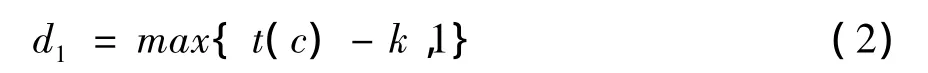
好后綴移動規則:模式串P與文本串T已經匹配的k個字符，稱為好后綴，記作suff(k)，如果模式P的前m-k個字符中可以找到一個最長字符組合v(len(v)＜k)是suff(k)的后綴，移動P使前m-k個字符的最右邊的v和suff(k)中的v對齊，此時v是和k相關的。好后綴移動的距離表示為:

取d=max(d1，d2)作為P向右移動的最大距離。

在算法的實現中，事先構建壞符號移動表和好后綴移動表，以減少在不同的c、v和k作用下查找和計算d值的次數，提高效率［4］。

3 一種改進的BM算法

3.1 BM算法的改進

傳統的BM算法中存在不必要的比較，當模式串在文本串中的初次匹配失敗后，可以根據文本串中當前窗口的下一個字符(即模式串和文本串左對齊后的最右側字符的下一個字符)決定偏移量，此時只使用壞符號移動規則。如果該字符在模式串中沒有出現，最大可以移動的位置為m+1。算法改進后模式向右移動的距離可以用公式4表示:

3.2 BM算法的改進的舉例

假設有文本串T和模式串P分別為，P:algorithm，T:this_is_boyer_mbore_algorithms，分析在改進的BM算法中，P匹配T的過程。生成的壞字符跳躍表如表1所示，對于模式P中出現過的字符“algorithm”，其對應的偏移量skip(c)是該字符在模式最右邊的出現位置距離模式最右側字符的長度，其它沒有在模式中出現的字符，其偏移量為m+1=10。

表1 壞字符跳躍表

T:this_is_boyer_mbore_algorithms

P:algorithm

第一次匹配:模式串的最右邊的字符“m”和文本串中的字符“b”比較，第一次字符比較失敗，此時當前窗口的下一個字符為“o”，根據表1知模式串P向右移動的距離為skip(o)=6。

T:this_is_boyer_mbore_algorithms

P:algorithm

第二次匹配:第一次比較模式串中的字符“m”和文本串中的字符“m”，匹配成功，繼續比較文本串中的字符“_”和模式串中的字符“h”，匹配失敗，此時當前窗口的下一個字符為“b”，根據表1知移動的距離為skip(b)=m+1=10，模式向右移動10個字符的位置。

T:this_is_boyer_mbore_algorithms

P:algorithm

第三次匹配:文本串中的字符“r”和模式串中的字符“m”比較，不匹配，當前窗口的下一個字符是“i”，根據表1，skip(i)=4，模式串 P向右移動4個字符位置。

T:this_is_boyer_mbore_algorithms

P:algorithm

第四次匹配:從模式串的尾字符“m”開始自右向左和文本串的相應字符依次比較，直到k=m，最終找到了模式串在文本串中的出現。

3.3 BM算法的改進前后的比較

根據改進的BM算法思想，抽取數據進行實驗驗證。在實驗中，隨機選取了4組樣本，模式串的長度基本不變取為8個字符，文本串的字符長度分別選取為500、1000、1500、2000，對于每組樣本，分別采用傳統的BM算法和改進后的BM算法，得到的字符比較次數和模式串的移動次數的情況如表2所示，每組樣本下模式移動次數的情況對比如圖1所示。

表2 BM算法改進前后字符匹配時比較次數和移動次數

在實際的字符查找應用中，初次比較不匹配、當前窗口的最后一個字符和下一字符不屬于模式串的情況是多數的。在這種情況下，采用改進的BM算法在每次的匹配中可以增加模式串的移動距離，從而減少比較的次數。

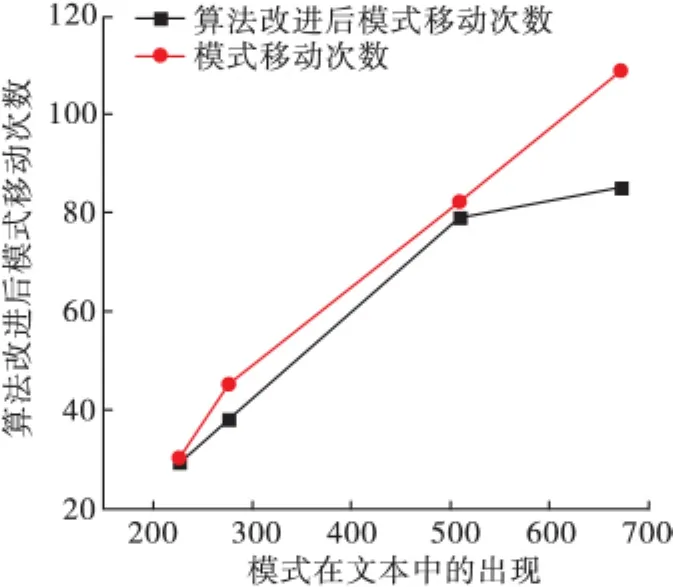
圖1 BM算法和改進BM算法比較次數和移動次數對比

4 結論

在傳統的BM算法中存在一些不必要的比較，增加了字符匹配時的比較次數，從而在實際的應用系統中導致系統效率不高。在改進的BM算法中，通過結合當前窗口的下一個字符的情況更改模式串的移動距離的長度，可以讓移動的距離增加1，最大能夠達到m+1。實驗數據表明，當文本串相對于模式串足夠長，模式串在文本串中的出現次數增加時，可以很大的提高算法的查找效率.

［1］韓光輝，曾誠.BM算法中函數shift的研究［J］.計算機應用，2013，33(8):2379-2382.

［2］孫文靜，錢華.改進BM算法及其在網絡入侵檢測中的應用［J］.計算機科學，2013，40(12):174-176.

［3］Anany Levitin.算法設計與分析基礎［M］.北京:清華大學出版社，2007.

［4］李韋男，虞慧群.一種改進的BM字符串匹配算法［J］.計算機工程與應用，2014，50(16):104-108.