基于AHP算法的仿真可信度模型的探討研究

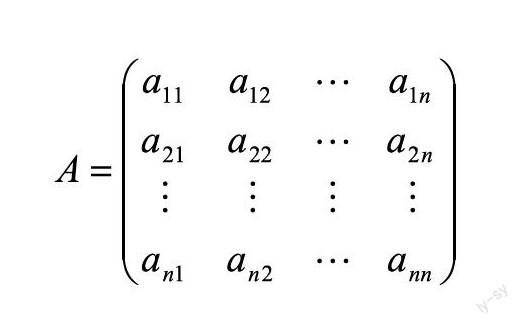

摘 要:提出了一種引入層次分析法來解決復雜系統仿真可信度計算問題的新思想:對復雜仿真系統進行功能層次分解,通過對其各層功能模塊的相對重要性進行兩兩比較構造出判斷矩陣,并對各層元素的權重進行排序和一致性檢驗,最后得到各層功能模塊的可信度相對于系統可信度的組合權重。基于這一思想,建立了基于AHP的可信度評估算法模型,為科學地解決可信度評估問題提供了一種新的思路。
關鍵詞:AHP算法,仿真可信度,算法模型
中圖分類號:F224-39 文獻標識碼:A
Abstract:A new idea by introducing the AHP method to calculate the fidelity of complicated simulation system.Based on the idea,the AHP credibility algorithm is presented.It offers a new clew to solve the problems of evaluating simulation credibility.
Keywords:AHP algorithm;simulation credibility;algorithm model
1 引言(Introduction)
根據AHP決策方法的特點與可信度評估的內在聯系,提出引入AHP決策方法來解決復雜系統仿真可信度計算問題的新思想[1,2]。以此設計了基于層次分析法的可信度評估算法模型,算法特點為:實現了經驗性評價和數學量化分析的轉化,將定量和定性進行了很好的結合;另外,總體的可信度中的因素:某一元素的可信度的誤差,不會對其有很大的影響[3]。
2 建立模型的具體算法(Specific algorithms for
building models)
在AHP算法基礎上,對仿真可信度進行綜合的步驟研究,建立AHP算法分析仿真系統可信度評估的基本算法模型。
2.1 構造判斷矩陣及標度
判斷矩陣是對每一層次中各因素相對重要性給出的判斷。假設B層元素Bk與下一層元素A1,A2,…,An有聯系,構造下述形式的判斷矩陣:
其中,aij為對Bk而言,Ai與Aj相對重要性的數值表示,通常采用1—9比率標度方法表示,其取值為1,2,3,4,5,6,7,8,9或它們的倒數:aij=1:Ai與Aj相等;aij=3:Ai比Aj略微強;aij=5:Ai比Aj強;aij=7:Ai比Aj很強;aij=9:Ai比Aj非常強;2,4,6,8表示的是相鄰判斷的中間值。使用上述標度方法的原因如下。
(1)當被比較的物質在需要采用的屬性上有相同的數量級或很接近的數量級時,定性的比較才有可行性和準確度。
(2)在評估事物本質上不同的時候,可以用相等、較強、強、很強、非常強這五種判斷很好表示;當需要高精度時,可以在相鄰的判斷之間作出比較。
(3)在同時刻進行比較時候,個項目是在心理學意義上面描述的極限度,如果這樣比較的話,項目之間的差異可用9個數字進行表示。
(4)若需要用比此更大的數,那么想要進行更好的分解聚類要使用層次分析法。
2.2 單一標準下元素的相對比重的計算方法
由Perron-Frobenius定理可知,通過解矩陣特征值問題,可得最大特征值及其對應的特征向量w:,式中,是矩陣A的最大特征值;w是對應的特征向量,w就是待尋找的各物體相對重要性的權重向量。
使用冪法來計算特征根,在仿真可信度評估中,正矩陣的最大特征值和特征向量的求解算法為:
(1)初始化:,,循環變量k=0。
(2)循環計算:
歸一化處理:,
已有,要判斷:。
若正確,是要得到的特征向量,要重新用上面公式再計算最大特征值,若不正確利用下面公式繼續計算:
2.3 一致性檢驗
判斷矩陣想要完全一致是非常難的,是由物質的復雜性和想法的多樣性決定的,但想要基本一致卻是可行的,因為如果判斷距離一致較遠時,可以通過排序權向量計算結果來進行判斷。計算后,仍需要進行一致性檢驗,公式為:
平均隨機一致性指標是對進行修訂而得到的,它反映了判斷矩陣階數對一致性的影響。用隨機方法構造1000個樣本矩陣,分別對階各1000個隨機樣本矩陣計算其一致性指標值,然后平均,即得到階平均隨機一致性指標值見表1。
為一致性比率,它是利用對進行進一步修正的結果:,當時,判斷矩陣的一致性可以采用,否則需要繼續調整判斷矩陣。
2.4 混合比重的計算方法
已有第層功能模塊上個元素和總體進行比較的權重排序向量,還有第層子功能模塊上個元素對第層功能模塊上第個元素為準則的權重排序向量為:
如果不受j控制的所有元素的所占的比重是0,那么,第層上所有元素在總體中混合權重排序向量是:
其中,為仿真系統功能層次數。如果第層就是最底層,則最底層各元素對于子系統可信度的影響權重可表示為。
對于逐層分析層次結構混合權重排序判斷如何檢驗一致性,需要使用相似的方法進行按層次進行計算,如果依次得到了第層次的計算結果、和,那么第層次的相應指標為:
在上面式子中,當滿足條件時,可以得到按順序分析求解的層次在第k層次的判斷具有相對可以通過采用的一致性。
3 結論(Conclusion)
作者基于引入層次分析法來解決復雜系統仿真可信度計算問題的新思想,對復雜仿真系統進行功能層次分解,通過對其各層功能模塊的相對重要性進行兩兩比較構造出判斷矩陣,并對各層元素的權重進行排序和一致性檢驗,最后得到各層功能模塊的可信度相對于系統可信度的組合權重。又通過上面的具體分析和仔細研究,大致實現了對復雜仿真系統中各節點的仿真可信度進行評估的算法設計,建立了基于AHP的可信度評估算法模型,為科學地解決可信度評估問題提供了一種新的思路。
參考文獻(References)
[1] Balci O. Validation,Verification and Testing Techniques throughout the Life Cycle of a Simulation Study[C].Proceedings of the 1994 Winter Simulation Conference,1994,215-220.
[2] Huey P Allen Jr,Peter B Burleson,Priscilla A Glasow.The Relationship of VV&A to T&E[A].Proceedings of the Summer Computer Simulation Conference,1998[C]:111-119.
[3] 魏華梁,等.系統仿真置信度研究中的若干問題與準則[J].系統仿真學報,2000,12(1):39-42.
作者簡介:
高婷婷(1981-),女,碩士,講師.研究領域:計算機科學與技術.

