讀懂有序數對

孔凡哲

對于“如何確定一個點”的問題，同學們可能都有自己的解決方法，其實，解決這個問題，既可以采用“形”的方法，也可以采用“數”的方法。

一、采用“形”的方法

（l）在一條直線上，如何確定一個點？

（2）在平面內，如何確定一個點？

對于上述問題，在直觀幾何中，自然好解決. 在直線上，只要知道一個已知點A以及未知點B到點A之間的距離，就可以大致確定未知點B，如果知道點B在點A的哪一側，那么，未知點B自然完全可以唯一確定，

而在平面內，確定一個點，正如我們知道的，兩條不重合的直線相交，可以得到一個交點，亦即，兩條直線可以確定一個點.

二、采用“數”的方法 在人類發展史上，“確定一個點”曾一度是儀有歐式幾何才能完成的任務，直到一位偉大的數學家笛卡兒出現，笛卡兒找到了一種奇妙的方法，這就是坐標法（借助代數表示，分析處理幾何問題，亦稱解析法）.從此，一個新的兒何學分支——解析幾何誕生了.

1.一維圖形上的點的坐標，

在數軸上.由于確定了原點、單位長度和正方向，確定一個點只需要一個數就可以了，這個數可以是有理數，也可以是無理數.

事實上.在數軸上，任意一個點P對應著唯一的數a，而任意一個數a也對應著唯一的點P，正如“一個蘿卜一個坑”.這個點P滿足OP=|a|，如果a是正數，那么，點P在原點O的右側（即數軸的正半軸上）；如果a是負數，那么，點p在原點O的左側（即數軸的負半軸上）；如果a是O，那么，點P與原點重合.

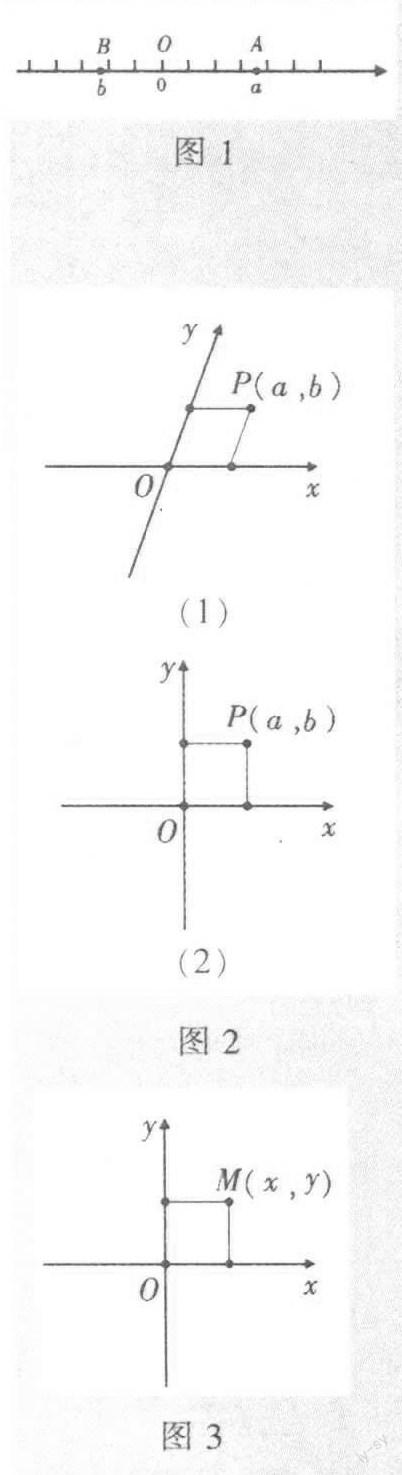
在數軸上，每一個點都對應著一個數，這個數其實就是這個點的坐標，在圖1中，點A的坐標是a，點B的坐標是b，點O的坐標是O.因此，數軸上的點，僅由一個代數量就可以唯一確定，于是，人們通常把直線叫作一維圖形.

2.二維圖形內的點的坐標.

在建立了兩個不平行的數軸的前提下，在平面內確定一個點，只需要一個數對就可以了——無論這兩條數軸是否垂直，

如圖2所示，圖2（1）中兩個數軸并不垂直，這就是斜坐標系；圖2（2）中的兩個數軸相互垂直，這就是我們通常所說的直角坐標系.

圖2（2）定位方式的本質在于，在由過同一個原點而且互相垂直的兩個數軸組成的圖形中，數對（X，y）可以表示平面內任意一點.此時，在平面內的任意一點也自然就有了它在兩個坐標軸上的對應位置，通過作垂線，尋找一個點在兩個坐標軸上分別對應的實數，于是，我們可以用一個有序數對表示這個點.如圖3所示，從點M分別向X軸、y軸作垂線，若垂足對應的數軸上的數分別為X、y，則可用數對（x，y）表示點M.值得注意的是，數對（X，y）是一個整體，數對的兩個數有位置之分，即有順序之分，是有序數對.

由于X軸、y軸都有正半軸、負半軸，兩個相互垂直的X軸、y軸就將平面劃分為兩條坐標軸與四個區域，這四個區域分別叫第一、二、三、四象限，根據點對應各坐標軸上數的屬性，四個象限內點的坐標有如圖4所示的特征.而坐標軸上的點（包括坐標原點）位于邊界上，不屬于任何一個象限，其中在X軸上的點縱坐標為O，在y軸上的點橫坐標為O.

例1 （2013年株洲）在平面直角坐標系中，點（1，2）位于第 _____象限.

分析與解答 根據各象限內的點的坐標特征解答.本題考查了各象限內點的坐標特征，準確識別各象限內點的坐標特征是解決本題的關鍵。

答案為第一象限.

三、確定-個點需要幾個條件

在直線上，確定一個點，僅僅需要一個代數條件即可，這就是數軸上的點對應的數，

在平面內，確定一個點，僅僅需要兩個獨立的代數條件就可以了，這就是平面直角坐標系內的橫、縱坐標.

四、如何確定常見的變換后點的坐標 初中階段將要系統學習圖形的變換形式，包括軸對稱變換、平移和旋轉等，采用點的坐標的變化來表達這些變換，其實更簡潔、更直觀.

1.軸對稱變換.

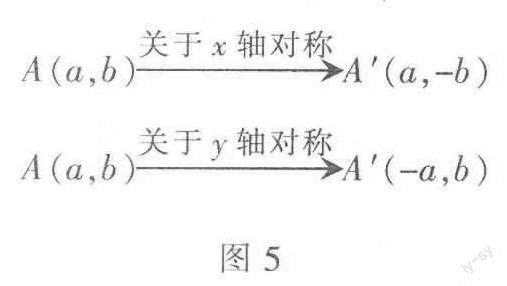
對于點與點之間的軸對稱變換，如果對稱軸是坐標軸，對稱點的坐標間的關系如圖5所示.

分析解答、根據關于X軸對稱的點的坐標特點“橫坐標不變，縱坐標互為相反數”即可解決，點P（X，y）關于X軸對稱的點P的坐標為（X，-y）.

因為點P（2，3）關于X軸對稱的點的坐標為（2，-3）.故答案為（2，-3）.

2.關于坐標原點對稱.

例3平面內一點P（a，b）：將其橫、縱坐標均乘以-1，對應點和點P之間有何關系？

分析解答、將平面內一點P（a，b）的橫、縱坐標均乘以-1后，對應點的坐標變為（-a，-b）.一個坐標變為相反數是岡為進行了一次關于坐標軸的軸對稱變換，于是，我們可以將上面的過程，描述為如圖6所示的過程，

從而，經過兩次軸對稱變換后的點，與原來的點關于坐標原點成中心對稱.

3.沿特殊方向的平移，

點沿著坐標軸左右或上下平移時，在平移過程中，點的坐標同樣發生變化，

對于平面內的任意一點P（a，b），經歷上述特殊方向的平移，其坐標間的關系如圖7所示.

4.點的復合式平移，

若平面內的一個點沿某一方向（非水平、非豎直的方向）移動，此時，我們只需要將其拆分成水平方向的平移與豎直方向的平移就可以了.當在水平、豎直方向都發生平移后，點的橫、縱坐標都發生變化，與先發生哪個方向的平移并沒有關系，

在數軸上，確定一個點，僅僅需要一個獨立的量就可以了.

在平面內，確定一個點，僅僅需要兩個彼此獨立的量就可以了，

你想過沒有？如果在我們居住的房間內確定一個點，那么，只需要幾個彼此獨立的量就可以了呢？