變式學習“平面直角坐標系”

張文娣

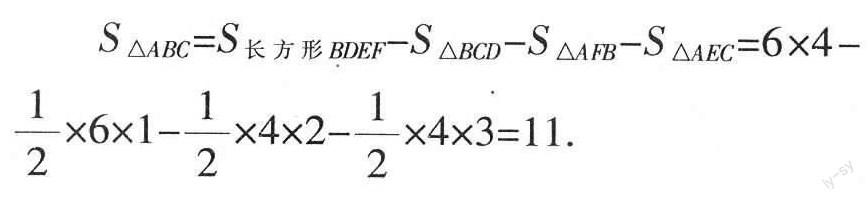
平面直角坐標系是繼數軸之后又一 個將數與形完美結合的工具'學好平面直角坐標系，不僅能讓我們更好地描述位置，表示平移，也能為我們以后學習函數打下良好的基礎.下面我們借助教科書上“平面直角坐標系”一章的一些問題進行變式學習.

例1（源自第64頁）如圖l，若第2列第3排記為（2，3），請以下座位的同學今天放學后參加數學問題討論：（1，5），（5，1），（2，4），（4，2），（3，3），（5，6）.其中（2，4）和（4，2）在同一個位置嗎？

解析：略

變式1“怪獸吃豆豆”是一種計算機游戲，圖2中的“.”表示“怪獸”先后經過的幾個位置.如果用（1，2）表示“怪獸”經過的第2個位置，那么你能用同樣的方法表示出圖中“怪獸”經過的其他幾個位置嗎？

解析：由（1，2）表示的位置可知，前一個數表示縱列，后一個數表示橫排.因此，“怪獸”經過的其他幾個位置分別為（1，1），（3，2），（3，3），（4，3），（4，5），（5，5），（5，4），（7，4），（7，3），（8，3）.

變式2（第65頁練習）如圖3，甲處表示2街與5巷的十字路口，乙處表示5街與2巷的十字路口.如果用（2，5）表示甲處的位置，那么“（2，5）→（3，5）→（4，5）→（5，5）→（5，4）→（5，3）→（5，2）”表示從甲處到乙處的一條路線，請你用這種形式寫出兩條從甲處到乙處的路線.

解析：所給路線是從甲處先向右再向下.

也可以從甲處先向下再向右，即沿路線“（2，5）→（2，4）→（2，3）→（2，2）→（3，2）→（4，2）→（5，2）”走，

還可以先向下走到4巷，再向右走到4街，然后再向下走到2巷，最后再向右走到5街，即沿路線“（2，5）→（2，4）→（3，4）→（4，4）→（4，3）→（4，2）→（5，2）”走.

變式3如圖4，如果（C，3）表示“天”，那么按以下方式排列分別能組成一句什么話？

（1）（A，5），（A，3），（C，4），（E，5），（B，1），（C，2），（B，4）.

（2）（B，4），（C，2），（D，4），（C，5），（A，1），（D，3），（E，1）.

解析：根據題意可知列在前，行在后，按照題中的表示方法找出相應的漢字，組成一句話即可.

（1）組成的一句話是“可愛的女孩是我”.

（2）組成的一句話是“我是一個小帥哥”.

變式4如圖5，在中國象棋的棋盤中，若黑“馬”現在的位置用（3，7）表示，且黑“馬”下一步不能走到（2，5），（4，5），（5，8）所示的位置，請你用有序數對表示出黑“馬”下一步可以走到的位置.

解析：黑“馬”現在的位置用（3，7）表示，可知前一個數表示列，后一個數表示行.因為“馬”走“日”字，所以黑“馬”下一步有5個位置可以走，分別是（1，6），（1，8），（2，9），（4，9），（5，6）.

例2（第71頁第13題）如圖6，右邊的“笑臉”是由左邊的“笑臉”平移得到的，找出幾對特殊的對應點，分別寫出它們的坐標，你能發現什么規律嗎？

解析：如圖7，點A'、B'、C'、D'分別是由點A、B、C、D平移得到的，觀察圖形可得A （-5，4），B（-3，4），C（-5，2），D（-3，2），A'（4，4），B'（6，4），C'（4，2），D'（6，2）.

可以發現，將圖形向右平移9個單位長度，圖形中各點的橫坐標都增加9，縱坐標不變.

變式1（第78頁第3題）如圖8，長方形ABCD的四個頂點分別是A（-3，2），B（-3，-2），C（3，-2），D（3，2）.將長方形向左平移2個單位長度，各個頂點的坐標變為什么？將它向上平移3個單位長度呢？分別畫出平移后的圖形.

解析：將長方形ABCD向左平移2個單位長度后，頂點A、B、C、D的坐標分別變為（-5，2），（-5，-2），（1，-2），（1，2）；將長方形ABCD向上平移3個單位長度后，頂點A、B、C、D的坐標分別變為（-3，5），（-3，1），（3，1），（3，5）.圖略.

變式2（第79頁第4題）如圖9，將三角形先向右平移2個單位長度，再向上平移3個單位長度，則平移后三個頂點的坐標分別是（）.

A.（2，2），（3，4），（1，7）

B.（-2，2），（4，3），（1，7）

C.（-2，2），（3，4），（1，7）

D.（2，-2），（3，3），（1，7）

解析：過程略，選C.

變式3（第79頁第8題）如圖10，三角形ABC中任意一點P（xo，Yo）經平移后對應點為P1（xo+5，yo+3），將三角形ABC作同樣的平移得到三角形A1B1C1求點A1、B1、C1的坐標.

解析：三角形ABC中任意一點P（xo，yo）經平移后對應點為P1 （xo+5，yo+3），橫坐標增加了5，說明點P向右平移了5個單位長度，縱坐標增加了3，說明點P向上平移了3個單位長度.

所以三角形ABC也應向右平移5個單位長度，向上平移3個單位長度，從而可得點A1（3，6），B1（1，2），C1（7，3）.

變式4求圖11中三角形ABC的面積.

解析：參照圖12所示的方式作輔助線，得到長方形BDEF

拓展：在平面直角坐標系中，點的橫坐標、縱坐標都是整數時，我們稱這個點為格點（也叫整點）.所有頂點都是格點的多邊形稱為格點多邊形.顯然，圖11中的三角形ABC就是格點三角形.

通過觀察，我們發現：在圖11中，三角形ABC的內部有10個格點，三角形ABC的邊界上有4個格點，且10+4/2-1=11.難道格點多邊形內的格點個數、邊界上的格點個數與格點多邊形的面積有關？我們一起來探究.

（1）在平面直角坐標系中盡可能多地畫出內部只有1個格點的格點三角形、格點四邊形、格點五邊形，計算這些格點多邊形的面積S，并數出邊界上的格點個數n，你能發現S與n之間有什么關系嗎？

（2）在平面直角坐標系中盡可能多地畫出內部只有2個格點的格點三角形、格點四邊形、格點五邊形，計算這些格點多邊形的面積S.并數出邊界上的格點個數n，你能發現S與n之間有什么關系嗎？

（3）在平面直角坐標系中盡可能多地畫出內部只有3個格點的格點三角形、格點四邊形、格點五邊形，計算這些格點多邊形的面積S，并數出邊界上的格點個數n，你能發現S與n之間有什么關系嗎？

（4）-般地，如果格點多邊形的面積為S，其內部的格點個數為m，邊界上的格點個數為n，你能根據（1）（2）（3）所得結果猜測S、m、n之間的關系嗎？再任意畫幾個格點多邊形試一試.

事實上，格點多邊形的面積公式為S=m+n/2-1（其中m表示格點多邊形內部的格點個數，n表示邊界上的格點個數），它也叫Pick定理.如果想進一步了解，請上網搜索相關知識.