幫你學習點的坐標
吳健
平面直角坐標系是溝通代數學和幾何學的橋梁,是極其重要的數學工具.
平面直角坐標系中有關點的坐標的問題在各類考試中經常出現,下面分別舉例說明如下.
1.特殊點的坐標.
(1)原點的坐標.原點的坐標是(0,0).
(2)坐標軸上點的坐標,x軸上點的坐標的特點是縱坐標為0,y軸上點的坐標的特點是橫坐標為0.
(3)象限的角平分線上的點的坐標,
第一、三象限的角平分線上點的橫坐標和縱坐標相等.如果點的橫、縱坐標相等,則它必在第一、三象限的角平分線上,
第二、四象限的角平分線上點的橫坐標和縱坐標互為相反數,如果點的橫、縱坐標互為相反數,則它必在第二、四象限的角平分線上.
(4)對稱點的坐標,
關于x軸對稱的兩個點的坐標的特點是橫坐標相等,縱坐標互為相反數,
關于y軸對稱的兩個點的坐標的特點是橫坐標互為相反數,縱坐標相等,
如果一個點的坐標為(a,6),那么這個點關于x軸、y軸、原點對稱的點的坐標分別是(a,-b),(-a,b),(-a,一b).
例1 若點P(5,a-3)與點Q(b-2013,-2013)關于x軸對稱,則a=____,b=____.若點P、點Q關于原點對稱,則a=____,b=____.
解:兩點關于x軸對稱,橫坐標相等,縱坐標互為相反數,則5=b-2013,a-3+(-2013)=0,所以a=2016,b=2018.兩點關于原點對稱,橫、縱坐標都變為原來的相反數,則5+b-2013=0,a-3-2013=0,所以a=2016,b=2008.
2.與幾何圖形有關的點的坐標.
在平面直角坐標系中,以任意兩點P(x1,Y1),Q(X2,y2)為端點的線段中點坐標為(x1+x2/2,y1+y2/2).
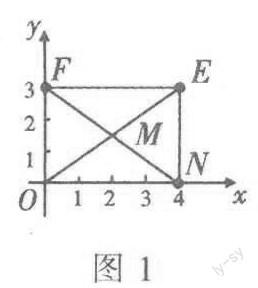
例2 如圖1,矩形ONEF的對角線交于點M0,ON、OF分別在x軸和y軸上,O為坐標原點,點E的坐標為(4,3),則點M的坐標為____.
解:因為四邊形ONEF是矩形,所以點M是OE的中點.
因為點O、E的坐標分別為(0,0),(4,3),所以點M的坐標為(2,3/2).
3.與面積有關的點的坐標.
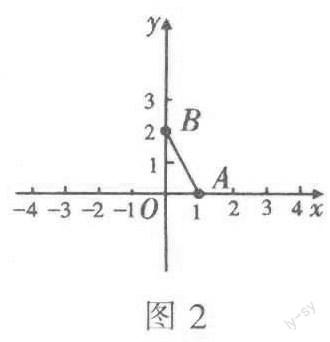
例3 如圖2,已知點A(1,0),B(0,2),若點P在x軸上,且三角形PAB的面積為5,則點P的坐標為____,
解:三角形PAB的一邊在x軸上,點p距點A有5個單位長度,點P可能在點A的右側,也可能在點A的左側,所以有兩個解,
填“(-4,0)或(6,0)”.

