基于壓縮感知的混沌成像雷達

唐駿 張璘 袁江南

【摘要】 匹配濾波器常用于雷達接收端，在寬帶雷達中，這會導致系統復雜且成本高昂。利用壓縮感知可以不用匹配濾波器和高速模數轉換器，且能實現高分辨雷達成像。鑒于雷達目標場景的稀疏性，提出一種用于混沌雷達的壓縮感知方法，用Bernoulli映射生成混沌調頻信號，利用該信號的隨機性，直接構造觀測矩陣。通過優化技術，可以由欠采樣的回波信號重構雷達景象。仿真了靜態和非靜態目標雷達景象，與匹配濾波處理相比，所提方法不僅處理簡單，且性能更優。結果驗證了該方法的可行性。

【關鍵詞】 混沌雷達 寬帶雷達 壓縮感知 匹配濾波器

一、引言

高分辨雷達成像技術對于雷達目標識別和特征提取具有重要意義，由雷達成像原理可知[1，2]，目標的距離向分辨率取決于發射信號的帶寬，方位向分辨率取決于相參積累時間。受Nyquist采樣定理的約束，傳統寬帶雷達成像系統面臨著采樣率高、數據量大、回波數據有限等諸多問題。

壓縮感知（compressed sensing， CS）[3-7]理論為寬帶雷達成像提供了一種新途徑。該理論表明，對于具有稀疏性的信號，通過少量次數的觀測，即信號的投影值就能精確或近似重構原信號。對雷達目標電磁散射特性的研究結果表明[8]，高頻區雷達目標脈沖響應可由少數重要散射中心來刻畫，寬帶雷達能得到的重要散射中心數遠小于識別這些散射中心所需的樣本數。除了壓縮感知，雷達信號的選擇直接影響距離-多普勒成像系統的性能。混沌信號用于雷達系統有許多獨特的優點，它們表現出隨機噪聲特性，具有頻帶寬、易產生等特點[9]。另一方面，頻率調制信號有高的成像分辨率，高輸出功率，低成本與低截獲、干擾概率等優點。

二、壓縮感知

壓縮感知理論出現在2000年左右，在隨后的幾年中得以迅速發展。CS 理論主要涉及三方面：信號的稀疏表示、信號的非相關采樣和信號的精確重構[10]。

2.1觀測矩陣

2.2重構算法

重構算法是指用低維的觀測信號y精確重構高維原信號x。目前，重構算法主要分為3類： 1） 基于l1范數的凸優化算法；2） 基于l0范數的貪婪算法；3） 組合算法。本文采用凸優化來重構雷達景象。凸優化方法是基于l1范數最小進行求解，相比于其它算法，重構效果較好。

三、基于壓縮感知的混沌成像雷達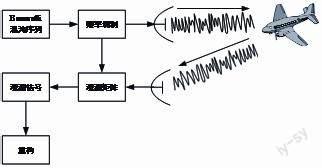

壓縮感知的混沌雷達系統框圖如圖2所示，混沌序列經頻率調制之后作為雷達發射信號，同時用來構成觀測矩陣，接收的回波通過與觀測矩陣運算得到觀測信號，利用優化算法，由觀測信號重構雷達景象。

混沌信號具有隨機噪聲的特征，自相關函數近似于δ函數，互相關函數近似為0，從上世紀九十年代開始，許多學者對混沌在雷達信號設計中的應用開展了研究，證明了混沌應用于雷達信號設計的可行性。研究內容集中在兩方面：混沌相位編碼信號和混沌調頻信號。在采用混沌序列進行調頻時，只有用Bernoulli映射產生的序列才能得到較理想的自相關特性[13]，因此本文用Bernoulli映射產生混沌序列，式（7）用來產生Bernoulli序列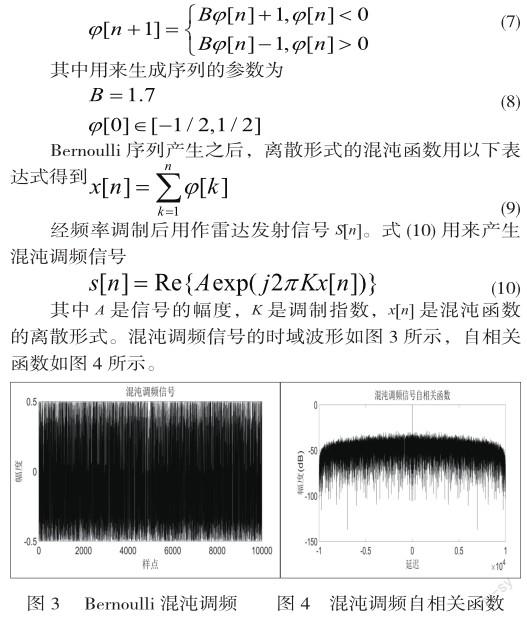

四、仿真及結果分析

4.1靜態目標仿真

雷達發射信號與目標卷積得到回波信號，為了用矩陣相乘來表示卷積運算，通過將混沌調頻信號S[n]移位來形成矩陣各列，由于混沌調頻信號具有類似噪聲特性，此矩陣在基于壓縮感知的混沌雷達系統中可用作觀測矩陣。

對于靜態目標，目標參數主要包括距離和散射系數，通過隨機放置具有不同散射系數的物體來模擬雷達景象，如圖5所示，其中橫坐標表示目標到雷達的距離，縱坐標表示目標的散射系數。仿真時，為了應用壓縮感知，觀測的信號應少于卷積結果的樣點數，可以通過下采樣觀測矩陣來實現。對于壓縮感知，觀測矩陣的各列需滿足不相關性。下采樣后的觀測矩陣各列的相關性如圖6所示。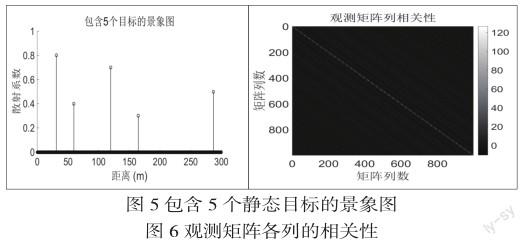

對于靜態目標，雷達景象通過2.2節中所說的凸優化技術來重構，如圖7所示，可以清晰看出，用壓縮感知，由欠采樣的樣點可以精確重構雷達景象。另外，圖8是利用匹配濾波器恢復的雷達景象。可以看出，匹配濾波器在恢復雷達景象的同時引入了許多噪聲，而且要求從回波中獲得足夠的樣點。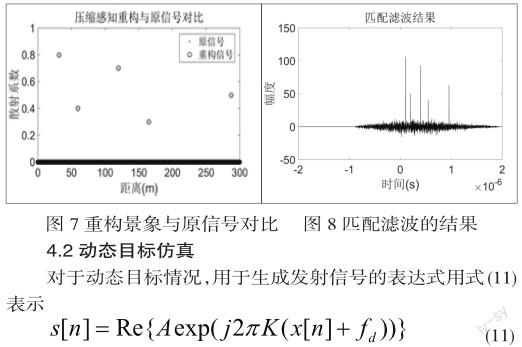

其中A是信號幅度，K是調制指數，x[n]是混沌函數的離散形式，fd是多普勒頻率。用于生成Bernoulli序列的參數與靜態目標情況相同。如前所述，生成的混沌調頻信號需要重排以形成觀測矩陣。與靜態目標情況不同，對于非靜態目標，每一個多普勒頻率需要移位所有距離維信號以形成觀測矩陣，如圖9所示。

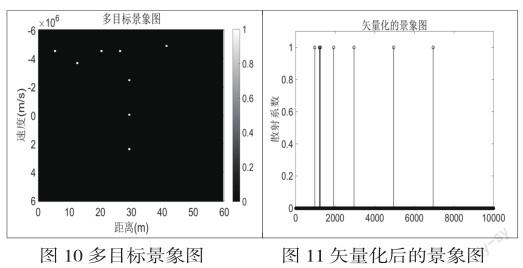
對于動態目標，目標的參數主要包括距離和多普勒頻率，可以用二維平面上的點來模擬，其中橫坐標表示距離，縱坐標表示目標的多普勒頻率。通過隨機放置目標生成二維的景象圖，如圖10所示。為了應用壓縮感知，景象圖需要化為一維矢量。該矢量表示，對于每一個多普勒頻率，重復所有可能的距離。圖10矢量化后的結果如圖11所示，圖10景象圖為100行、100列，化為一維矢量即長度為10000。

跟靜態目標情況一樣，為了應用壓縮感知，觀測矩陣與接收信號需要下采樣。在接收端，通過凸優化技術重構雷達景象，如圖12所示。圖13是壓縮感知重構與原信號的對比圖。圖14是用匹配濾波器恢復的雷達景象。可以看出，匹配濾波器引入了大量的噪聲，這些干擾可能會掩蓋目標或很難區分靠得近的目標。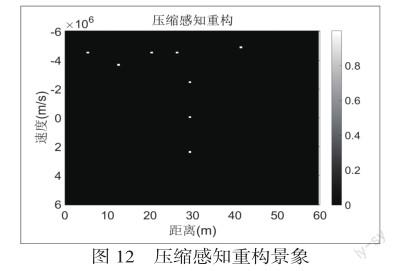

五、結束語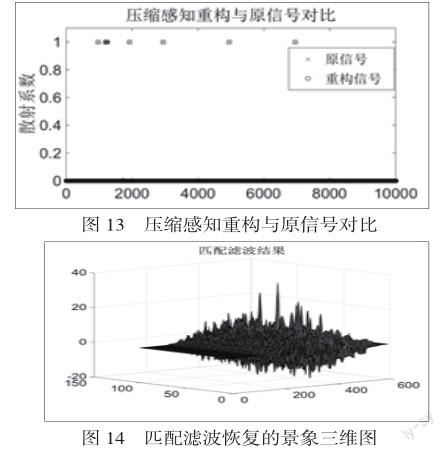

提出了一種用來提高混沌雷達分辨率的壓縮感知方法。用Bernoulli映射生成的混沌序列經調頻后用作發射信號，該信號具有類隨機噪聲特性，其模糊函數近似于“圖釘”形，且可直接用來生成觀測矩陣。仿真了靜態和非靜態目標雷達景象，與匹配濾波法進行了比較。對于靜態目標，雷達景象包含了目標的距離和散射系數，回波信號通過觀測矩陣后下采樣，應用優化技術，從下采樣的接收信號中可以恢復雷達景象。與匹配濾波法相比，壓縮感知所需數據量小，抗噪聲性能好。對于非靜態目標，雷達景象包含了目標的距離和速度。該情形下，匹配濾波器雖然能夠恢復雷達景象，但同時引入了許多噪聲，使得目標難以辨識。相比之下，即使接收信號下采樣，壓縮感知也能精確恢復雷達景象。仿真結果表明，基于壓縮感知的混沌雷達系統結構簡單，無需匹配濾波和高速的模數轉換器，數據處理量小，十分適用于寬帶高分辨雷達的應用。

參 考 文 獻

[1] Richards M A. Fundamentals of Radar Signal Processing [M]. Second Edition， McGraw-Hill Education， 2014.

[2] Mahafza B R. Radar Systems Analysis and Design Using MATLAB [M]. CRC press， 2000.

[3] Donoho D L. Compressed sensing [J]. Information Theory， IEEE Transactions on， 2006， 52（4）： 1289-1306.

[4] Malloy M L， Nowak R D. Near-optimal adaptive compressed sensing [J]. Information Theory， IEEE Transactions on， 2014， 60（7）： 4001-4012.

[5] Candès E J， Wakin M B. An introduction to compressive sampling [J]. Signal Processing Magazine， IEEE， 2008， 25（2）： 21-30.

[6] Gangopadhyay D， Allstot E G， Dixon A M R， et al. Compressed sensing analog front-end for bio-sensor applications [J]. Solid-State Circuits， IEEE Journal of， 2014， 49（2）： 426-438.

[7] Zhang Shun-sheng， Zhang Wei， Zong Zhu-lin， et al. High-resolution Bistatic ISAR Imaging Based on Two-dimensional Compressed Sensing [J]. Antennas and Propagation， IEEE Transactions on， 2015， 63（5）： 2098 -2111.

[8] Wang Li-bo， Tan Yun-hua. A Novel Approximate Solution for Electromagnetic Scattering by Dielectric Disks [J]. Geoscience and Remote Sensing， IEEE Transactions on， 2015， 53（5）： 2948-2955.

[9] Yang Qi-lun， Zhang Yun-hua， Gu Xiang. Wide-Band Chaotic Noise Signal for Velocity Estimation and Imaging of High-Speed Moving Targets[J]. Progress In Electromagnetics Research B， 2015， 63： 1-15.

[10] 徐建平. 壓縮感知算法在雷達成像中的應用研究 [D]. 電子科技大學， 2012.

[11] Candès E J. The restricted isometry property and its implications for compressed sensing [J]. Comptes Rendus Mathematique， 2008， 346（9）： 589-592.[12] 張磊， 柏業超， 張興敢. 壓縮感知在寬帶雷達信號處理中的應用[J]. 南京大學學報： 自然科學版， 2014， 50（1）： 35-40.

[13] Flores B C， Solis E A， Thomas G. Chaotic signals for wideband radar imaging [C]//AeroSense 2002. International Society for Optics and Photonics， 2002： 100-111.