“幾何圖形初步”的學習要點

孔凡哲　帥帥

“幾何圖形初步”是《義務教育數學課程標準（2011年版）》中“圖形與幾何”的重要內容之一。

扎實掌握“幾何圖形初步”的核心內容，是學好“圖形與幾何”的關鍵，對于初中數學學習至關重要。

一、了解“幾何圖形初步”的學習目標，掌握與之適應的學習方法

“幾何圖形初步”的基本內容涵蓋了點、線、面、角等，這些內容是幾何學的核心組成要素。通過學習，需要我們努力達成如下目標：

1.通過實物和具體模型，了解從物體抽象出來的幾何體、平面、直線和點等。

2.會比較線段的長短，理解線段的和、差，以及線段中點的意義。

3.掌握基本事實：兩點確定一條直線。

4.掌握基本事實：兩點之間線段最短。

5.理解兩點間距離的意義，能度量兩點間的距離.

6.理解角的概念，能比較角的大小。

7.認識度、分、秒，會對度、分、秒進行簡單的換算，并會計算角的和、差。

恰當的方法是學好“幾何圖形初步”的利器，為此，我們需要掌握以下學習方法：

1.重視概念，仔細體會其數學本質，杜絕機械記憶，重視對概念的理解，可以結合圖形或圖形間的轉化理解概念，例如，可以結合我們的活動經驗來理解幾何的概念，將筆在紙上輕輕一點，就形成了一個點，將這個點按照一個方向一直運動就形成了射線，將這條射線圍繞著起始點進行旋轉，就形成了角，這樣結合活動在運動中理解幾何概念，不失為一個好方法.

2.充分利用生活經驗，深化對于幾何基本事實的理解，對于本章的一些內容，不僅需要我們理解概念，而且需要我們認識“兩點確定一條直線”“兩點之間線段最短”等重要的基本事實，這些基本事實是數千年以來人類不斷積淀的生活經驗，需要我們還原生活，從幾何學的角度進行再次提升，“兩點確定一條直線”其實是“在墻上釘木條（如果忽略摩擦力），用兩根釘子，就能釘牢”等生活經驗的進一步提煉，而“兩點之間線段最短”幾乎被許多生物的本能反應所詮釋，無論是狗撲食，還是鳥兒被驚飛，生物的本能促使它們都選擇最快捷的途徑。

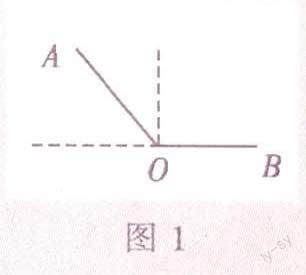
3.借助圖形理解概念——這是幾何學不同于代數學的關鍵點之一，例如，鈍角的定義是“大于直角且小于180°的角”，但是在實際觀察中發現，很多同學都會漏掉小于180°的角這個重要條件，如果通過圖1來理解定義，就不會出現類似的問題了。

4.注意培養看圖、畫圖的能力，本章與以往的代數學習的重要差別之一就是幾何直觀能力，表現在圖形上就是識圖、辨圖、畫圖的能力，同學們首先要學會看簡單圖形，將簡單圖形的畫法、基本特征、性質銘記于心，逐漸養成在復雜圖形中尋找簡單圖形，將復雜圖形分解為若干個簡單圖形的習慣。

圖形的發展推進了人類生活上產的進程

就人類的發展而言。圖形的出現遠遠早于文字，而數學起源于人類生產生活的需要，“圖形與幾何”的產生就是源于面積測量的需要，相傳4000年前，古埃及的尼羅河每年洪水泛濫，淹沒兩岸的土地，也帶來肥沃的淤泥，洪水退后，土地的界線便不再分明，當時的人們為了重新測出被洪水淹沒的土地的界線，每年總要進行土地測量，古埃及人積累了許多土地測量方面的知識，積淀了幾何學初步的豐富經驗。

我國對幾何學的研究也有悠久的歷史，在公元前1000年前，我國處于黑陶文化時期，陶器上的花紋就有菱形、正方形等許多幾何圖形，公元前500年，在墨翟所著的《墨經》里有幾何圖形的相關知識，《九章算術》里記載了土地面積和物體體積的計算方法，《周髀算經》里記載了直角三角形三邊之間的關系，這就是著名的勾股定理，也被稱為“商高定理”，祖沖之的圓周率也是著稱于世的，還有我國古代數學家劉徽、王孝通等，都對幾何學做出了重大貢獻。

隨著工農業生產和科學技術的不斷發展，幾何學的知識也越來越豐富，研究的方面也越來越多，因此，“圖形與幾何”是為了解決現實問題而存在的，對于我們的生活是必要的。

三、實現世界中存在多姿多彩的幾何圖形

幾何圖形是由現實世界的實物抽象而來的，幾何圖形裝點著我們的大千世界，在現實世界中，存在著各種各樣的幾何圖形，有的是簡單的幾何圖形，有的是由簡單幾何圖形復合而成的復雜幾何圖形。

有些幾何圖形（如線段、角、三角形、長方形、圓等）的各部分都在同一平面內，它們是平面圖形，有些幾何圖形（如長方體、圓柱、圓錐、球等）的各部分不都在同一平面內，它們是立體圖形。

我們生活的世界完全可以說是一個圖形的世界。圖2和圖3就是筆者在生活中拍攝的照片，從中可以發現很多的幾何圖形，其中，既有平面圖形也有立體圖形，例如，平面圖形：圓、長方形、鈍角、直角等，立體圖形：球、圓臺等，你也可以試著找一找，看看還能找出哪些幾何圖形。

只要我們仔細觀察，認識思考，就會發現幾何圖形無處不在。

幾何直觀能力是指借助于見到的（或想象出來的）幾何圖形，對數學的研究對象（即空間形式和數量關系）進行直接感知、整體把握的能力，借助于直觀形象的圖形，我們可以簡捷明快地分析和解決數學問題，通過本章的學習，期望你初步認識圖形，感受圖形世界的美妙，體會圖形世界的內在規律——它們都是由一些基本圖形組成的。

當然。僅僅找到它們是不夠的，我們更應該去思考：用所學的幾何圖形知識，可以解決哪些問題呢？

四、動手制作立體圖形，積累幾何操作的直接經驗，發展空間觀念

“圖形與幾何”的應用之一就是設計制作文化用品和家居用品，這些物品是人們生活中必不可少的工具，它們在幫我們解決生活問題的同時也美化了生活環境，圖4、圖5是我們生活中常見的小家具——收納凳，它們既可以幫我們收納物品，也可以供人們休息。

原本一個收納用的箱子，經人們稍加設計，就變得更有用了，現在市面上一般都是正方體的收納凳（圖4）和正八棱柱的收納凳（圖5），

1.發現數學問題，

能否用已經學過的知識來開發出新樣式的收納凳呢？

我們一起來研究如何制作一個正五棱柱的收納凳。

2.提出數學問題，

將我們待解決的問題——“制作一個正五棱柱的收納凳”，轉化成數學問題——“如何制作一個正五棱柱”。

3.分析問題，

觀察正五棱柱，它有什么樣的特點呢？可以發現正五棱柱的上表面和下表面是一樣的正五邊形，側面都是一樣的矩形，并且這些矩形都有一邊與正五邊形的邊長相等。

4.解決問題。

（1）設計正五棱柱的展開圖，

不難分析，展開圖需要滿足這樣的條件：上表面和下表面至少要有一條邊與側面連接，而側面之間則不必完全連接。

正五棱柱的展開圖大致分為兩類：

當側面都連在一起時，只要兩個一樣的正五邊形在側面所連成的大矩形的兩側即可（如圖6所示）：

當側面和側面不連接在一起時，那么有一個正五邊形就會和每一個側面都連接，另一個正五邊形和其中的一個側面的矩形連接即可（如圖7所示）。

這兩類展開圖均可組成正五棱柱，

（2）任選一個第一步中可以組成正五棱柱的展開圖（如圖8），將展開圖按連接線折起，用膠粘住，一個正五棱柱就做好了。

5.幾何知識的拓展應用。

經過前面發現問題、提出問題、分析問題、解決問題四步，我們就能夠做一個正五棱柱了，細心的同學可以發現，筆筒是生活中的物品，它與正五棱柱是有區別的，這就引起我們注意了，將所學的數學知識應用于實際生活時，應該根據具體情況做一些處理。

我們要做正五棱柱的收納凳，還要注意下面幾個問題。

（1）用一些承重能力強的材料，按照上面的步驟制作兩個不完整的正五棱柱（一個沒有下表面，另一個沒有上表面，并且沒有下表面的正五棱柱要比沒有上表面的正五棱柱大一點），我們就可以仿照制作正五棱柱的步驟去制作沒有上表面（或下表面）的正五棱柱。

（2）將這兩個不完整的正五棱柱套在一起。

（3）創意加工：給兩個不完整的正五棱柱先穿上“美麗的衣服”，然后進行精心“化妝”、適當鏤空，再加些小飾物，一個正五棱柱的收納凳就大功告成了。

能力拓展：經歷了上面的過程，你不妨想一想圓柱體、正三棱柱、長方體的收納凳或者筆筒應該如何制作，利用類似的圖形，你還可以做什么樣的富有創意的小物品呢？

懂得了數學知識，我們也可以自己做各種有創意的家具了！只要認真思考，數學會帶給我們無盡的驚喜！認識和了解了幾何圖形之后，我們會發現數學知識很有用，可以幫我們解決生活中的問題，能夠讓生活更美好，為我們的生活增光添彩。

同學們還能發現圖形的哪些應用呢？

練一練

1.圖9、圖10、圖11可以折成什么樣的立體圖形呢？

2.圖12是正六棱柱的展開圖（不完整），如果要用這個展開圖折成一個正六棱柱，需要添上什么圖形，在哪添，共有幾種添法？

3.圖13是正六棱柱的展開圖（不完整），要補充完整，需要添上什么樣的圖形，可以添在什么位置上，共有幾種添法？

參考答案：

1.圖9：三棱錐；圖10：圓錐；圖11：正六棱柱。

2.添一個和圖12中一樣的正六邊形。共有6種添法，位置略。

3.需要添上和圖13中一樣的正六邊形，共有6種添法，位置略。