初論幾何圖形

田載今

數學是研究數量關系（簡稱“數”）和空間形式（簡稱“形”）的科學。人類在認識客觀世界的過程中，會遇到大量關于“數”與“形”的問題，小孩兒最早接受的數學啟蒙教育，是最直觀的“數”與“形”，他們往往從數手指頭開始，認識了1、2、3、4、5等整數，在搭積木等游戲中，認識了三角形、正方形、圓、長方體等圖形。提起數學，人們往往首先想到“數”，其實“形”在數學中是與“數”地位相當的，并且“數”與“形”有著緊密的聯系。

一、幾何圖形是從物體形狀中抽象出的數學概念

我們身邊的物體都有各自的形狀，幾何圖形是人們從豐富多彩的物體形狀中抽象出的數學概念，例如，人們對滿月、車輪、硬幣等物體的形狀進行抽象概括，發現這些物體的形狀都符合“一中同長”的特點，即周邊各點到中心一點的距離都一樣長，為研究具有這一特點的物體形狀，人們得出了圓的定義，即平面上到一個定點的距離等于定長的所有點的集合叫作圓，這個定點叫作圓心，定長叫作圓的半徑，這里的圓，已經脫離了滿月、車輪、硬幣等物體的其他性質，只反映這類物體共同的形狀特征。它是一種幾何圖形，恩格斯對幾何圖形的產生給出了精辟的總結：“‘形的概念完全來自外部世界，而非頭腦憑空想出，對客觀存在的物體形狀加以比較，才得出‘形的概念。”

幾何學是研究“形”的數學分支，它的英文單詞為geometry，其中geo表示土地，metry表示測量，器物制造、土地測量等實際需要，是幾何學產生的原動力，人們在長期的實踐活動中。對來自現實世界的幾何圖形進行了深入研究，不斷獲取經驗，發現規律，并加以系統整理。使得具有嚴密邏輯體系的幾何學逐步形成，幾何圖形的形狀、大小和位置等，是幾何學研究的主要問題，按研究對象和研究方法的不同。幾何學可分為歐氏幾何、非歐幾何、解析幾何、射影幾何、微分幾何、代數幾何等，其中，歐氏幾何因古希臘數學家歐幾里得而得名，它最早成型，是最基礎的幾何體系，而且對整個數學向公理化方向發展起了重要的推動作用，同學們在初中數學中所學習的幾何知識都在歐氏幾何范疇內。

二、幾何圖形的組成

幾何圖形形態各異，變化萬千，有繁有簡，最簡單的幾何圖形是孤立的一個點，它只表示空間中的一個位置，而沒有大小的規定，畫圖時筆尖接觸一下紙就畫出一個點，筆尖在紙上連續移動，所經過的不同位置分別對應空間中不同的點，這些點組成一條不間斷的線，這就是“點動成線”，作為幾何圖形，任何線段（包括直線段和曲線段）都只計長短而不計粗細，線在空間中連續運動（平移、旋轉等），其運動軌跡可以形成一個平面圖形或曲面圖形。這就是“線動成面”，封閉的平面圖形或曲面圖形都只計邊界長短、面積大小而不計厚薄，面在空間中連續運動（平移、旋轉等），其運動軌跡可以形成一個立體圖形，這就是“面動成體”，封閉的立體圖形一般只計邊界長短、表面積大小、體積大小。

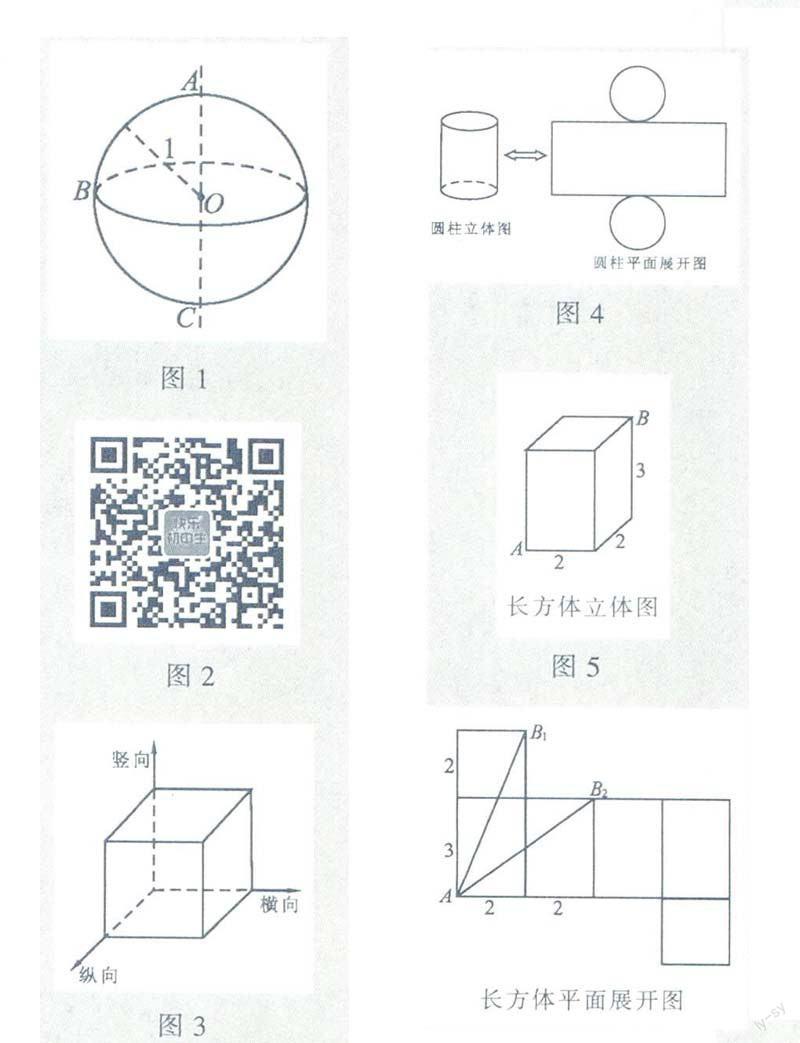
復雜圖形可以分解為若干簡單圖形，點是組成幾何圖形的最基本的元素，每個幾何圖形都是符合一定條件的點的集合，例如，以點O為中心、半徑為1的球面（如圖1），是由空間中所有到點O的距離等于1的點組成的集合，它也可以看作半圓弧ABC繞直線AC旋轉一周形成的曲面，

幾何學中，平面是一個不加定義的原始概念，平面平如鏡子，它不計厚薄，沒有邊界，可以向各個方向無限延伸。

幾何圖形可以分為兩類：如果構成圖形的點都在同一平面上，則這個圖形屬于平面圖形，例如直線、三角形、四邊形、圓等；如果構成圖形的點不全在同一平面上，則這個圖形屬于立體圖形，例如長方體、圓柱、球等，在歐氏幾何中，以平面圖形為主要研究對象的部分，叫作平面幾何，以立體圖形為主要研究對象的部分，叫作立體幾何。

對于平面圖形和立體圖形，可以這樣想象：

構成平面圖形的點，是在一個不計厚薄的平面上運動，點的運動軌跡上的任一位置，由橫、縱兩個方向上的位置所確定，這類似于在平房教室中，每個學生的座位由座次表上的橫向排號和縱向列號兩個數所確定，這兩個方向稱為兩個維度，所以平面圖形也叫二維圖形，現在常用的二維碼（如圖2），是按一定規律在平面上黑白相間地排列而得到的圖形，它記錄了特定的數據符號，由于它是用平面圖形表達信息的，所以叫作二維碼。

構成立體圖形的點，是在一個像盒子一樣的空間里運動，點的運動軌跡上的任一位置。由橫、縱、豎三個方向上（如圖3）的位置所確定，這類似于在有不同樓層的劇場中。每個觀眾的座位由入場券上的橫向排號、縱向列號和豎向樓層號三個數所確定，這三個方向稱為三個維度，所以立體圖形也叫三維圖形，我們能直觀感受到的外部空間是三維空間，所以三維圖形也常被稱為空間圖形，通常所說的3D電視，就是能使畫面產生立體視覺效果的電視，

平面圖形與立體圖形在一定條件下可以互相轉化，如圖4，圓柱是立體圖形，把組成它的各個面平鋪開來，所得展開圖是平面圖形：反過來，把圓柱的平面展開圖折起。各個面又圍成立體圖形，認識立體圖形時，通常先從它包含的平面圖形人手，這種研究方法是“降維處理”，但是，不是任何立體圖形都有平面展開圖，例如，球的表面是一個完整的曲面，它不能嚴格地展開成平面圖形，我們只能設法得到其平面近似展開圖，繪制世界地圖時，會用到這種近似展開方法。

例1如圖5，一只螞蟻在長方體上的點A處，它要沿我們能看到的面爬到點B處，最短路程是多少？

解：觀察圖5，根據經驗可知，螞蟻要想以最短路程從點A處爬到點B處，至少要經過長方體的兩個面（即經過正面與上底面或經過正面與右側面），畫出長方體的平面展開圖（如圖6），圖5中的點B對應圖6中的B₁、B₂兩個點，兩個點之間的最短路徑是連接這兩個點的線段，比較線段AB₁和線段AB₂，通過測量可以發現AB₁>AB₂，故在圖5中，從點A處出發，經過正面與右側面到達點B處的路徑（對應圖6中的線段AB₂最短，按圖中標注的尺寸，可以通過測量、計算得到最短路程為5。

三、直線是原創幾何圖形

幾何學有嚴格的邏輯順序，如果要給一種幾何圖形下定義，定義中出現的其他圖形必須是此前已明確的概念，因此，在邏輯鏈條的起始端，必然要有一些只作描述而不加定義的原始幾何圖形，它們是以后衍生出其他一系列幾何圖形定義的基礎，點、直線、平面等都是原始幾何圖形。

直線無定義，對它只有描述性的解釋，如像一根拉緊的細線，沒有彎曲之處，不計粗細，可以向兩個方向無限延伸等，直線概念既來自于實際原型（如拉緊的細線等），又高于實際原型，其中包含了人類豐富的想象力（如無限延伸等），直線是動點朝兩個相反的方向移動的軌跡，從運動方向的角度看，沿一條直線的運動最簡單，例如物體在自由下落的過程中，方向始終豎直向下，物理中把這類運動稱為直線運動。

一條直線上有無數個點，這些點有序地排列在直線上，中間不存在“空位”，這體現了直線上點的有序性和連續性，人們正是利用這些性質發明了數軸這一表示實數集合的直觀模型。

無數次實踐驗證了一個基本事實：在空間中任意選取兩個點，經過它們能且只能畫出一條直線（如圖7），人們把它歸結為一條公理（即直接承認的真理）：兩點確定一條直線，這里的“確定”包含了“存在性”（一定有過這兩個點的直線）和“唯一性”（過這兩個點的直線只有一條），幾何學中，像這樣有雙重含義的“確定”廣泛地存在著，如：不在同一直線上的三個點確定一個圓（如圖8），不在同一直線上的三個點確定一個平面（如圖9），

有了直線這一原始幾何圖形，就可以用它定義射線和線段這兩種基本幾何圖形，直線上的一個點和它一側的那一部分叫作射線，直線上的兩個點和它們之間的那一部分叫作線段，顯然，射線無限長，它表示了一個確定的方向，線段有長度，“兩點之間線段最短”是幾何學中的又一條公理，一條線段的長度就是線段的兩個端點之間的距離。

例2空間中有n個點，其中任意三個點不在同一直線上。以這些點為端點的線段共有6條，

（1）求n的值，

（2）設A、B、C是這n個點中的任意三個，線段AB、AC、BC之間有什么關系？

解：（1）以這n個點中的任意兩個為端點，可以連出一條線段，所以每個點均可與另外（n-1）個點連出（n-1）條線段，以兩個點為端點的線段僅有一條，所以線段的總條數為

（2）如圖10，因為A、B、C三個點不在同一直線上，線段AB是A、B兩個點之間的最短路徑，A→C→B是從點A到點B的另一條路徑。所以AB

線段是直線上有限長、不間斷的一部分，它的長度容易理解，由線段組成的幾何圖形屬于直線形，例如三角形、四邊形、五邊形等，直線形的度量和計算（周長、面積等）建立在線段長度的基礎上，例如三角形的周長C=a+b+c。

直線有一個特性是處處不彎曲，有些幾何圖形不具有這種性質，例如圓弧是處處彎曲的線，它屬于曲線，含有曲線的幾何圖形屬于曲線形，曲線形的度量和計算要比直線形復雜，例如推導圓的周長公式和面積公式要比推導三角形的周長公式和面積公式難得多，

能否通過“化曲為直”使曲線形的計算變得容易呢？我們看看魏晉時期的數學家劉徽是怎么做的，如圖11，劉徽先把圓周六等分，連接各等分點，得到圓內接正六邊形；在此基礎上，再把圓周十二等分，連接各等分點，得到圓內接正十二邊形……繼續下去，使圓內接正多邊形的邊數不斷加倍，則圓內接正多邊形的面積就越來越接近圓的面積，正多邊形是直線形，它的面積相對容易計算，通過計算邊數不斷加倍的正多邊形的面積，可得到圓的面積越來越精確的近似值，可以想象，當邊數充分大時，圓內接正多邊形與圓幾乎重合，劉徽用這種“割圓術”計算出圓的面積高精度的近似值，并求出圓周率的近似值3.14，這在當時是非常輝煌的成就，可以發現，劉徽的“割圓術”是通過無限細分的方法，使微小的圓弧段轉化為與之極為相近的微小線段，這種“化曲為直”的方法與思想。和后來出現的微分方法、極限思想高度一致。

幾何圖形中蘊涵了豐富的數學知識，隨著學習的深入，同學們會不斷提高對它們的認識。

責任編輯：潘彥坤