歐拉的“砝碼問題”
蔣明玉
在歷史上,論勤奮與對數學的貢獻,很難有哪位數學家能夠與歐拉相比,
歐拉往往能從被人們忽視的現象中提出有創新意義的數學問題,開辟數學科學中新的領域。
如天平的砝碼是用天平稱物的重要工具,那么準備怎樣的一組砝碼,在只允許將其放在天平的一端的情況下,可以保證稱出砝碼總克數以內的所有整克數的物品呢?
下面是歐拉研究過的“天平砝碼最優(少)化配置問題”,同學們能獨立試著做一做,并得出規律嗎?讓我們一起來試一試,
問題1:工人師傅用質量為15g的一個鐵塊制成4個質量不等的整克數的砝碼,用這一組砝碼,在只允許將其放在天平的一端的情況下,可以稱出質量為15g以內的所有整克數的物品,這一組砝碼分別是幾克?
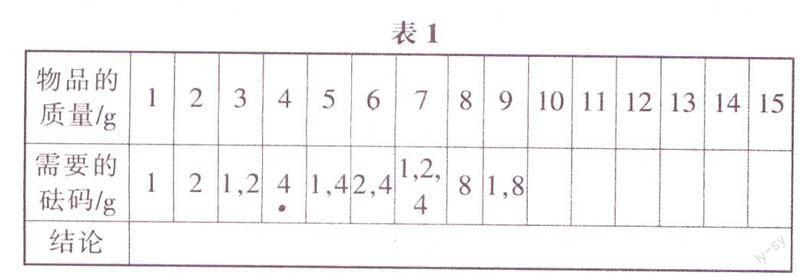
思考:可以從稱1g的物品開始分析,完成表1,
從而得到結論:稱質量為15g以內所有整克數的物品,只要準備質量為1g,2g,4g,8g這4個砝碼,
如果到此為止,僅解決這一個問題,那么,就不算具有愛思考的好習慣了,讓我們來分析這一組砝碼,可以有下面幾點發現:
1.這一組砝碼的克數是一組有規律的數:1,2,22,23,
2,它們的和正好比這組數的下一項少1,即它們的和為:24-1,
根據上面的發現,可以得到以下假設:
若有質量為1g,2g,22g,23g,…,2ng的砝碼,只允許將其放在天平的一端,利用它們可以稱出質量小于2n+1g的任何整克數的物體,
請你舉例驗證一下,
如果同學們再一起來解決下面的問題,會有新的發現的,
問題2:有一個質量為40g的砝碼,現在把它加工成4個質量是不等整克數的砝碼,允許將其放在天平的兩端,可以用它們稱質量為1g至40g之間的任意整克數的物體,這4個砝碼的質量分別是多少?
思考:可以參考前面的研究過程來進行實驗,具體步驟如下:
1.制表,2.填表,3.得到結果,4.研究結果,5.發現規律,6.進行驗證,
不難發現,這4個砝碼的質量分別是1g,3g,9g,27g稱出質量為2g的物體,把質量為1g的砝碼放在左邊,質量為3g的砝碼放在右邊,利用3-1=2就可以了,質量為4g的物體可利用3+1=4稱出質量為5g的物體可利用9-4=5稱出,其他類似,
通過上面的6個步驟,相信你也能得到最后的規律:若有質量為1g,3g,32g,33g,…,3ng的砝碼,允許將其放在天平的兩端,利用它們可以稱出質量不超過(3n+1)/2g的任何整克數的物體,
責任編輯:胡云志
- 中學生數理化·七年級數學人教版的其它文章
- 本期檢測題、易錯題專練參考答案
- 娜子姐姐信箱
- 數學創新思維競賽
- 斐波那契與“兔子數列”
- 圖形的計數
- “雙雪”時伴半夜讀

