譜聚類算法及其在SAR圖像分割中的應用研究

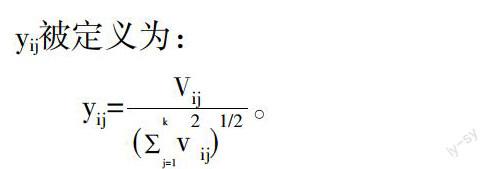
摘 要：譜聚類算法作為一種高效的智能聚類算法被廣泛地研究與應用，它與傳統的聚類算法相比，具有明顯的優勢。文章首先對譜聚類理論進行了概述，介紹了圖劃分準則、譜松弛及譜聚類算法，后介紹算法在SAR圖像分割中的應用，并對分割時出現的一些問題加以分析和討論，對研究譜聚類算法及其對SAR圖像的分割具有一定得理論參考。

關鍵詞：譜聚類；SAR圖像；圖像分割

中圖分類號：TP391.41 文獻標識碼：A 文章編號：1006-8937（2015）29-0046-02

1 譜聚類算法

譜聚類算法基于譜圖劃分理論，它將聚類問題看成是圖的劃分問題，使用數據樣本的相似度矩陣的特征向量進行聚類。該算法對凸型的球形空間或非凸的任意空間的聚類表現不敏感，易于得到全局最優解，較傳統聚類算法（K-means和最大期望值EM算法）優勢明顯，是當前流行的一種高性能聚類算法。利用譜聚類算法實現圖像的分割是人們較感興趣的一個研究方向。

圖的最優劃分其實是一個NP難問題，有效的解決辦法就是對原問題進行實數域松弛，進而可將圖的劃分轉換為求解矩陣的特征值和特征向量問題。對于合成孔徑雷達圖像（簡稱SAR圖像）的分割來講，譜聚類算法除了要考慮圖像的光譜特性、空間特征等因素，還要考慮算法的計算速度及內存消。

2 譜聚類理論及算法實現

2.1 譜聚類理論算法

得到圖G的一個最優二分圖即是對公式（1）最小化，但這種做法傾向于獲得不均衡、歪斜的劃分。基于2-way劃分的規范割判據（Ncut）可以克服這種現象，其目標函數為：

將x松弛至連續實數域 ，求解minNcut（A，B）的問題可以轉化為下式（4）的優化問題：

根據Rayleigh商原理的知識，我們可將對（4）式的優化問題轉化為式（5）中特征值和特征向量的求解問題。

2.2 譜聚類的圖像分割方法實現步驟

雖然第二最小特征值？姿2所對應的特征向量x2（也稱Fiedler向量）包含了豐富的圖劃分信息。但僅僅根據x2對數據進行迭代性聚類，不僅計算效率低且聚類結果不穩定。研究發現，同時使用多個特征向量可以避免由于信息損失造成的不穩定性，并且直接進行k路分割可以得到更好的聚類效果。一種基于多路劃分譜聚類的圖像分割方法實現步驟。

2.2.1 預處理

2.2.2 譜映射

2.2.3 聚 類

將Y的每一行看成是k維空間Rk中的一個樣本，通過K-Means算法將這些樣本聚成k類，當且僅當Y的第i行被分配為j類時才將圖像的像素點vi分配為j類。

3 關于SAR圖像分割的兩大問題

SAR圖像不同于醫學圖像、紋理圖像和彩色圖像的分割，由于其圖像本身的特點，如成像機理、對比度、一致性、信息熵、灰度共生矩陣、小波能量等特征，直接采用傳統的分割方法往往不能夠得不出較好的分割結果。針對SAR圖像的分割問題值得討論。

3.1 構造相似度問題

對于SAR圖像的分割缺乏標準統一的相似度構造函數，目前針對這方面的研究，國內外許多研究、科研人員進行的大量工作。如：提取一窗口大小中像素點的小波能力、灰度共生矩陣等特征，并計算窗口內像素點的平均特征構造相似度矩陣；另一種方法是，首先對采用分水嶺算法得出的特征塊集合X聚成k 個子集合進行預處理，再使用高斯核函數構造相似度矩陣。3.2 時空復雜度問題

對于一個包含n個像素點的圖像（如一副256×256的圖像，n=28×28）來講，算法的計算復雜度數量級為n3，往往致使計算機內存溢出和處理器計算時間過長。對內存的高消耗和處理器的計算速度優化問題顯得尤為重要。典型的一種減少計算復雜度的方法是Fowlkes等人提出的Nystrom算法，該方法使用優化標準割準則對目標函數進行優化、逼近，并對矩陣特征矩陣進行稀疏，提取出典型特征方式來減少計算量。另一種是基于形態學分水嶺的技術，并結合譜聚并結合譜聚類算法的聚類優勢得出的一種多階段聚類算法。該算法也能夠大大降低構造相似性矩陣時的計算量。

4 結 語

本文介紹了譜聚類的理論基礎及算法實現原理，并給出了基于譜聚類的SAR圖像分割方法。最后，對SAR圖像的分割問題加以分析，并對SAR圖像的分割研究方向加以引導，對基于譜聚類算法的合成孔徑雷達圖像和航拍圖像的目標定位和識別研究具有一定的理論參考和指導意義。

參考文獻：

[1] Luxburg U V.A tutorial on spectral clustering [J].Statistics and Computing，2007，（4）.

[2] 葛洪偉，李志偉，楊金龍.基于局部密度估計和近鄰關系關系傳播的 譜聚類[J].模式識別與人工智能，2014，（9）.

[3] 李志偉，葛洪偉，楊金龍.基于鄰里關系傳播與模式合并的譜聚類[J].計算機工程，2014，（6）.

[4] 李志偉.基于近鄰傳播和密度信息的譜聚類算法研究與應用[D].無 錫：江南大學物聯網工程學院，2014.

[5] Shi Jianbo，Malik J.Normalized cuts and image segmentation [J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，（8）.

[6] 賈建華，焦李成.空間一致性約束譜聚類算法用于圖像分割[J].紅外與毫米波學報，2010，（1）.

[7] Fowlkes C，Belongie S，Chung F，et al.Spectral grouping using the Nystrom method[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2004，（2）.