基于Pade逼近的時滯對電力系統穩定器的影響分析

胡亞莉 張亮 許嘉紋 劉振國

【摘要】低頻振蕩對電力系統穩定性的影響很大，目前通常用PSS來抑制，但電力系統信號時滯對PSS的性能有一定影響。本文通過Pade分析時滯對PSS控制器的影響，并用MATLAB進行仿真驗證，分析數據并得出結論。

【關鍵詞】Pade 時滯分析 電力系統穩定器 MATLAB仿真

電力系統的穩定性是研究電力系統的最基本也是最重要的問題之一，但是伴隨著電網規模擴大，大量快速勵磁裝置的投入使用，以及大量不穩定的新能源接入，電力系統運行的穩定性也越來越接近臨界點，因振蕩而導致失穩的問題越來越普遍，其中低頻振蕩問題尤為突出。

電力系統穩定器（PSS）是抑制低頻振蕩常用手段，通常是以本地功角，角速度等本地信號作為輸入，輸出疊加到勵磁系統，作為一種發電機勵磁側的附加控制。但是，本地信號對區間模式的可觀性不高，控制效果不佳。廣域測量系統（WAMS）可以在同一個時間坐標下，捕捉到電力系統各地點實時的穩態、動態信息，這些信息可以廣泛應用到電力系統穩態及動態分析以及控制的諸多領域中。但是它存在信號時滯的問題，而時滯信號會大大降低控制器的性能。因此，含有信號時滯的PSS分析和研究就有其現實意義。本文通過電力勵磁系統模型，針對含有信號時滯的PSS，使用Pade逼近的方法進行了分析，計算了各次逼近的時滯穩定裕度，并利用MATLAB進行仿真分析。

一、Pade逼近的位置選擇

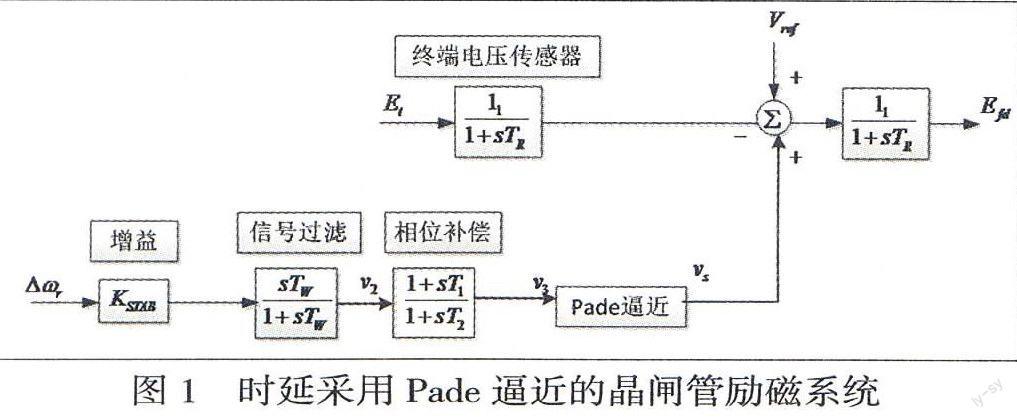
Pade逼近的位置選擇很重要，一般比較合適的位置是置于相位補償環節之后，如圖1所示：

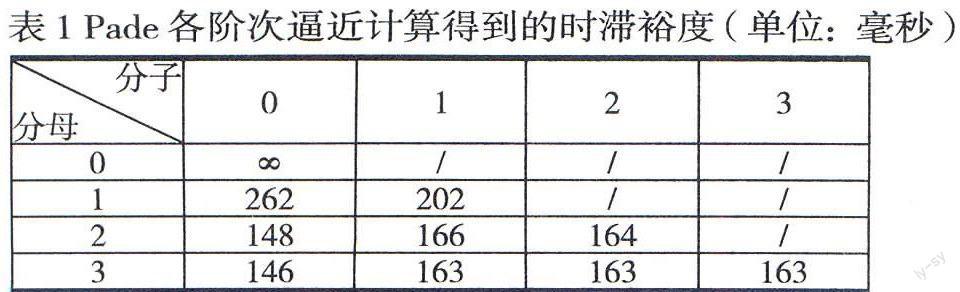
通過經典算法對時延進行處理，表1為計算的時滯穩定裕度：

表中∞表明沒有時延。通過表l可以看出，一階逼近計算的值較大，二階、三階的分子非零次逼近計算的結果相近，考慮到階數越高逼近越精確，因此可以得知一階逼近的效果不好。綜合考慮計算量和計算的時滯裕度，二階、三階逼近結果相近，因此選擇二階分子非零逼近Pade逼近效果比較好。

二、MATLAB仿真分析

采用分子分母均為二階的Pade逼近，對單機無窮大系統系統進行時域仿真。表3.2的分析結果，下面針對單機無窮大系統進行MATLAB仿真，具體參數為：

圖2-5給出了PSS反饋信號分別在延時146ms、160ms、166ms、266ms的轉子角速度和功角增量動態響應曲線不同時延下系統角速度和功角的零輸入狀態下響應曲線。

通過對仿真結果圖2-5的分析，可以得出以下結論：

①反饋信號時延對電力系統穩定器的影響非常大，隨著時延的增加，系統的穩定性越來越差，當時延增大到一定程度，系統失穩，發生自發振蕩。

②系統能承受的最大時延在160-165ms之間，表1中計算出三階內Pade各次逼近的最大時延，從表中可以看出，一階逼近的結算結果在200ms以上，而系統在200ms就已經失去了穩定，證明一階逼近的效果不好。高階逼近在分子為常數的情況下，計算結果偏小，從仿真結果可以看出系統在150ms時，仍然具備穩定特性。二階、三階的Pade逼近效果較好，計算出的最大時滯穩定裕度與實際比較接近，而考慮到逼近階數越高計算量越大，所以以二階逼近效果最優。

三、結論

綜上分析，通過選擇合適的階次，Pade逼近能夠比較準確的對時延進行近似處理，計算出系統的時滯穩定裕度，并且階次越高，計算越精確。但同時可以看出，Pade逼近的階次越高，計算越復雜，耗費的時間越多，不同階次的計算結果不一樣，如何快速選擇合適的逼近階次需要進一步研究。除此之外，Pade逼近只能針對固定時延，對于變時滯無法給出保守性證明。