活用伸縮變換 巧解高考橢圓問題
——以2015年全國部分省市高考試題為例

●楊瑞強 (黃石市第一中學 湖北黃石 435000)

活用伸縮變換 巧解高考橢圓問題
——以2015年全國部分省市高考試題為例

●楊瑞強 (黃石市第一中學 湖北黃石 435000)

2)直線 Ax+By+C=0變換成直線Aax'+ Bby'+C=0，斜率為原來的倍(特別地，當直線垂直于坐標軸時，變換后依然垂直于坐標軸);

3)若點A，B，C共線，則變換后點A'，B'，C'依然共線，且對應長度的比值不變，如=

4)伸縮變換前直線與橢圓相切(相交、相離)，伸縮變換后直線與橢圓依然相切(相交、相離);

5)伸縮變換前圖形的面積S與伸縮變換后圖形的面積S'滿足關系S=abS'.

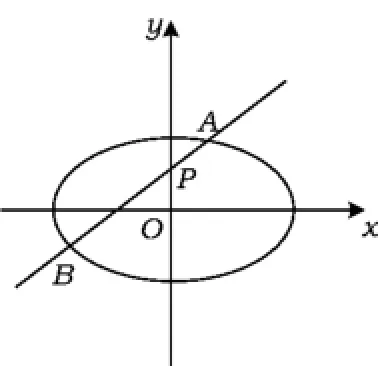
圖1

1)求橢圓E的方程.

2)在平面直角坐標系xOy中，是否存在與點P不同的定點Q，使得恒成立?若存在，求出點Q的坐標;若不存在，請說明理由.

因此，若存在與點P不同的定點Q滿足條件，則點Q的坐標只可能為Q(0，2).下面證明:對任意的直線 l，均有

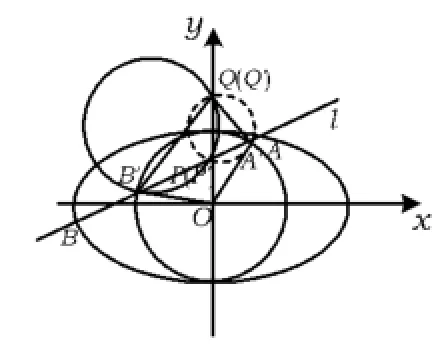
圖2

由OA'2=OB'2=OP'·OQ'知，直線OA'，OB'分別是△P'A'Q'，△P'B'Q'外接圓的切線.因為∠OA'P'=∠OB'P'，所以

∠P'Q'A'=∠P'Q'B'，

從而 tan∠P'Q'A'=tan∠P'Q'B'，

即

評析 探究定點是否存在，若假設定點坐標直接求解，則有不少運算障礙;若先通過特殊直線將定點找出來，再證明(驗證)一般情形，完成解答則相對簡單.本題采用后者，這樣在整理式子或求值時就有了明確的方向.另外，本題在證明一般情形時，采用伸縮變換，將橢圓轉換成圓，借助圓的基本知識加以解決，最后又回到了橢圓中，達到了化繁為簡的目的.

1)求橢圓C的方程;

②求△ABQ面積的最大值.

(2015年山東省數學高考理科試題第20題)解 1)橢圓C的方程為(過程略).

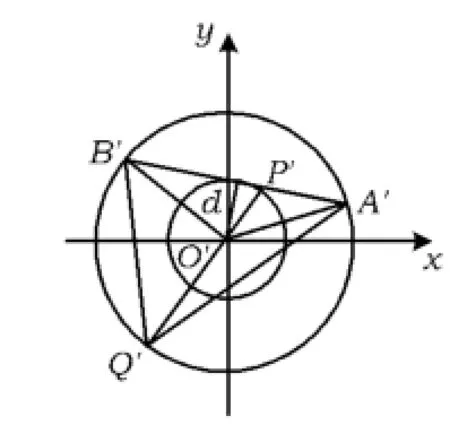
圖3

②由①知，S△A'B'Q'=3S△A'B'O'，設O'到直線A'B'的距離為d，則

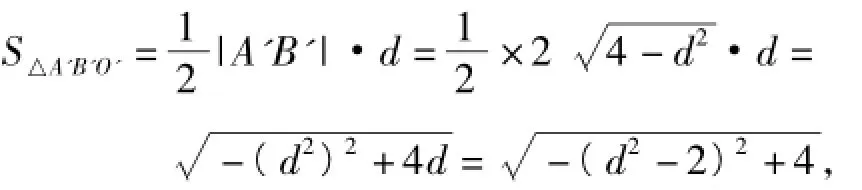
評析 在遇到與橢圓有關的問題(如面積問題、平行問題、斜率問題等)，可以先把橢圓變換成圓，在圓中解決問題當然容易得多，然后根據變換的可逆性及其性質，從而使橢圓中的問題快速求解，這樣不但避免了大量而繁瑣的運算，而且思路十分流暢.

例3 一種作圖工具如圖4所示.O是滑槽AB的中點，短桿ON可繞O轉動，長桿MN通過N處鉸鏈與ON連接，MN上的栓子D可沿滑槽AB滑動，且DN=ON=1，MN=3.當栓子D在滑槽AB內作往復運動時，帶動N繞O轉動一周(D不動時，N也不動)，M處的筆尖畫出的曲線記為C.以O為原點、AB所在的直線為x軸建立如圖5所示的平面直角坐標系.

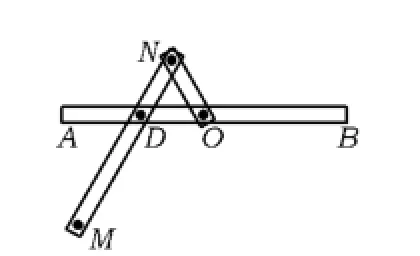
圖4

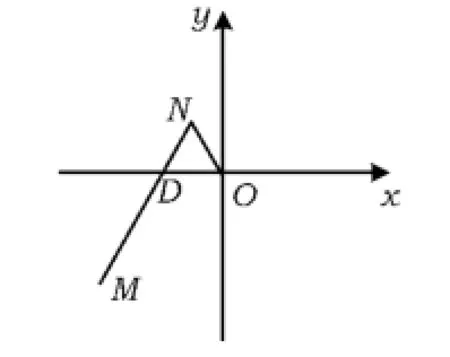
圖5

1)求曲線C的方程.

2)設動直線 l與2條定直線 l1:x－2y=0和l2:x+2y=0分別交于點P，Q.若直線l總與曲線C有且只有1個公共點，試探究:△OPQ的面積是否存在最小值?若存在，求出該最小值;若不存在，說明理由.

(2015年湖北省數學高考理科試題第21題)

位圓C':x'2+y'2=1，2條定直線 l1:x－2y=0和l2:x+2y=0依次變換成l1':x'－y'=0和l2':x'+ y'=0，原坐標系下的點P，Q，O依次變為新坐標系下的點P'，Q'，O'.

若直線l總與橢圓C有且只有1個公共點，則l與橢圓C相切，即PQ與橢圓C相切，從而P'Q'與圓C'相切，于是

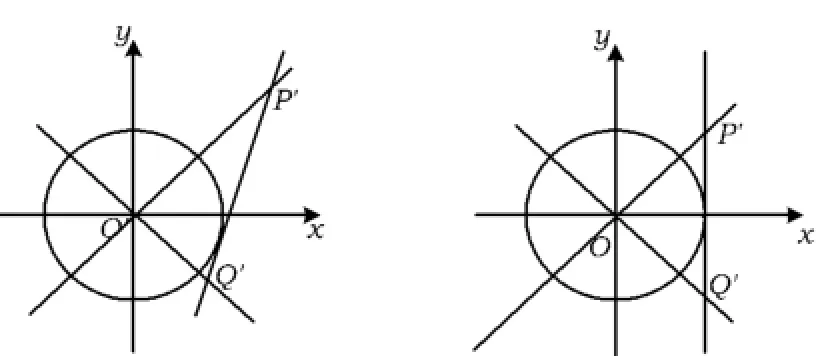
圖7

根據圖形(如圖7)觀察可知，當切點在圓與坐標軸交點處時，|P'Q'|取得最小值，且|P'Q'|min=2，此時

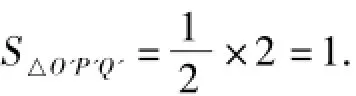
根據伸縮變換的性質，有S△OPQ=ab·S△O'P'Q'=8S△O'P'Q'≥8，即(S△OPQ)min=8.

故當直線l與橢圓C在4個頂點處相切時，△OPQ的面積取得最小值8.

評析 本題第2)小題，利用伸縮變換，將橢圓變換成圓，問題即轉化成尋求S△O'P'Q'的最小值，結合圖形，很容易找到|P'Q'|取得最小值(當切點在圓與坐標軸交點處)時，S△O'P'Q'有最小值，形象直觀;然后利用伸縮變換的性質，得到S△OPQ的最小值，起到變難為易的作用，大大減少了思維量與計算量.

總之，從變換的角度看，把圓“壓”一下即成橢圓，橢圓也可以再“伸”一下還原成圓.在研究直線與橢圓的位置關系時，利用伸縮變換將橢圓轉化為圓后，往往可以避免聯立方程組這一繁瑣的程序，而將問題轉化到直線與圓的位置關系這一大家非常熟悉的問題中來，使得原來隱于橢圓內的一些幾何關系得以顯性化.然后可以利用圓的有關性質加以解決，從而達到簡化運算的目的.

［1］ 魏國兵.讓橢圓“圓”形畢露——淺談伸縮變換在高考橢圓問題中的應用［J］.數學教學，2014(5):5-13.