電力系統(tǒng)機組組合問題研究綜述

劉艷芳，夏昌浩

(三峽大學(xué)電氣與新能源學(xué)院，湖北 宜昌 443000)

電力系統(tǒng)機組組合問題研究綜述

劉艷芳，夏昌浩

(三峽大學(xué)電氣與新能源學(xué)院，湖北 宜昌 443000)

機組組合問題是電力系統(tǒng)優(yōu)化運行的重要組成部分，一直是電力系統(tǒng)研究中的熱點和難點。總結(jié)了傳統(tǒng)機組組合數(shù)學(xué)模型及經(jīng)典求解方法，并在此基礎(chǔ)上介紹了近年來基于市場、節(jié)能等因素用于機組組合問題求解的新型智能優(yōu)化算法，綜述了機組組合問題的發(fā)展和應(yīng)用現(xiàn)狀，并展望了未來有待進(jìn)一步研究的內(nèi)容。

機組組合；啟發(fā)式算法；數(shù)學(xué)優(yōu)化算法；智能優(yōu)化算法

1 引言

隨著我國電網(wǎng)全面推進(jìn)精益化的調(diào)度管理和節(jié)能發(fā)電調(diào)度的實施，電網(wǎng)運行部門對安全經(jīng)濟(jì)運行的要求日益提高，機組組合問題的研究和應(yīng)用也越來越受到重視，作為電力系統(tǒng)運行調(diào)度理論的核心[1]，幾十年來，機組組合問題一直是電力系統(tǒng)研究中的熱點和難點。合適的機組組合能夠在電力系統(tǒng)短期運行中實現(xiàn)對發(fā)電資源的結(jié)構(gòu)性優(yōu)化，滿足系統(tǒng)的調(diào)峰和備用需求，為電力系統(tǒng)經(jīng)濟(jì)調(diào)度及安全校核提供基礎(chǔ)[2]；同時，能夠提升高能效大機組的運行效率，盡可能使機組運行在最佳工作點，提升系統(tǒng)的經(jīng)濟(jì)性和節(jié)能性。

機組組合問題是一個包含多個約束條件的大規(guī)模非線性混合整數(shù)優(yōu)化的問題，在數(shù)學(xué)上難以求得精確最優(yōu)解[3]。傳統(tǒng)的機組組合問題是指在滿足系統(tǒng)負(fù)荷要求和各類機組約束條件下，確定未來一定期間內(nèi)各機組的開停機時間和出力情況，使系統(tǒng)的總運行費用達(dá)到最小。多年來，研究者們對機組組合的模型及求解方法進(jìn)行了大量的研究，提出了各種滿足不同系統(tǒng)及運行要求的數(shù)學(xué)模型和求解方法[4-8]。

本文總結(jié)了傳統(tǒng)機組組合數(shù)學(xué)模型及經(jīng)典求解方法，并在此基礎(chǔ)上介紹了近年來國內(nèi)外出現(xiàn)的新模型及新方法，綜述了機組組合問題的發(fā)展和應(yīng)用現(xiàn)狀，并展望了未來有待進(jìn)一步研究的內(nèi)容，通過探討未來機組組合發(fā)展的方向及亟待解決的問題，使之能夠適應(yīng)智能電網(wǎng)的發(fā)展，制定滿足安全、節(jié)能、環(huán)保和經(jīng)濟(jì)的發(fā)電計劃。

2 機組組合數(shù)學(xué)模型

2.1 目標(biāo)函數(shù)

機組組合問題在不同的社會發(fā)展階段具有不同的數(shù)學(xué)表達(dá)模型，傳統(tǒng)模式下，機組組合問題的優(yōu)化目標(biāo)通常是系統(tǒng)成本最小，包括發(fā)電機組的開、停機成本和運行成本等，機組組合問題的最終目標(biāo)函數(shù)可表示為使機組運行和啟停等狀態(tài)轉(zhuǎn)換所消耗的總煤耗成本最低[9]，具體表示如下：

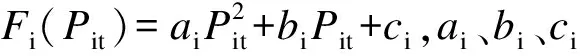
隨著機電力工業(yè)市場化改革的進(jìn)行及越來越多地考慮到環(huán)境、能耗等因素，機組組合問題的數(shù)學(xué)模型也在傳統(tǒng)模型的基礎(chǔ)上有了一些細(xì)節(jié)性改變。由于電力工業(yè)市場化的改革，機組組合目標(biāo)函數(shù)開始表示為資源配置率或社會總收益最大。文獻(xiàn)[10]在傳統(tǒng)模型基礎(chǔ)上，增加負(fù)荷跟蹤和快速旋轉(zhuǎn)備用的限制，建立與備用協(xié)調(diào)優(yōu)化的機組組合模型，將目標(biāo)函數(shù)表示為發(fā)電成本與備用成本之和；文獻(xiàn)[11]闡述了考慮到節(jié)能發(fā)電因素時，機組組合優(yōu)化目標(biāo)函數(shù)表示為系統(tǒng)能耗最低或污染物排放最少；文獻(xiàn)[12]闡述了在低碳電力調(diào)度模式下，機組組合優(yōu)化目標(biāo)表示為最大限度地減少CO2的排放。

2.2 約束條件

傳統(tǒng)的機組組合模型中考慮的約束條件有：

(1)系統(tǒng)功率平衡約束

(2)熱備用約束

(3)機組出力限制

Pi,min≤Pit≤Pi max

(4)機組爬坡能力約束

(5)機組最小運行及停運時間限制

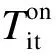
在實際運行狀況中，為了得到更加符合系統(tǒng)實際運行要求的發(fā)電計劃，在研究機組組合問題時，開始考慮一些新的約束條件，諸如機組動態(tài)技術(shù)約束、環(huán)境約束、網(wǎng)絡(luò)安全約束和市場約束等約束條件相繼出現(xiàn)在機組組合模型中。

3 機組組合求解方法

不同時期的機組組合問題具有不同的目標(biāo)函數(shù)和約束條件，但是它們的求解算法基本與傳統(tǒng)機組組合問題的求解算法相同，其求解算法可大致分為三類：

(1)啟發(fā)式算法(含窮舉法、優(yōu)先順序法)；

(2)數(shù)學(xué)優(yōu)化算法(含動態(tài)規(guī)劃法、拉格朗日松弛算法、混合整數(shù)規(guī)劃法等)；

(3)智能優(yōu)化算法(含遺傳算法、模擬退火算法、粒子群算法、蟻群算法、人工神經(jīng)網(wǎng)絡(luò)算法、免疫算法等)。

其中前兩類屬于求解機組組合問題的經(jīng)典算法，多年來在機組組合問題求解上已得到廣泛應(yīng)用；智能優(yōu)化算法通過程序模擬自然界已知的進(jìn)化方法從而達(dá)到優(yōu)化的目的，其中諸如模擬退火算法、粒子群算法等方法近年來被研究者們應(yīng)用到了機組組合問題求解中，得到了較好的效果。

3.1 啟發(fā)式算法

啟發(fā)式方法(Heuristic Method HM)是最早使用的一類優(yōu)化方法,這種方法沒有嚴(yán)格的理論依據(jù),依靠直觀的判斷或?qū)嶋H調(diào)度的經(jīng)驗尋找最優(yōu)解，啟發(fā)式方法在機組組合問題中的應(yīng)用有兩種情況，即窮舉法和優(yōu)先順序法。

3.1.1 窮舉法

窮舉法(Exhaustive Enumeration，EE)是求解機組組合問題中最早出現(xiàn)的一種方法，該方法通過列舉發(fā)電機組的所有可行組合來求解，在所有可行組合中，運行成本最低的機組組合狀態(tài)即為機組組合問題的最優(yōu)解。該方法理論上能為機組組合問題提供精確解，但是需要列出機組組合問題的所有可行狀態(tài)，故該方法只適合求解小規(guī)模機組組合問題。文獻(xiàn)[13]指出機組的調(diào)度與負(fù)荷的經(jīng)濟(jì)分配是密不可分的一個整體，將系統(tǒng)可靠性引入待求的成本函數(shù)，并運用窮舉法求得了成本最小時的最優(yōu)方案。

3.1.2 優(yōu)先順序法

優(yōu)先順序法(Priority Listing，PL)將系統(tǒng)可調(diào)度的機組按某種經(jīng)濟(jì)特性指標(biāo)事先排出順序,根據(jù)系統(tǒng)負(fù)荷大小按這種順序依次投切機組。該方法應(yīng)用簡便，計算速度快，占用內(nèi)存少，能滿足一般的應(yīng)用要求，但是該方法常常不能找到最優(yōu)解。優(yōu)先順序法提出較早，現(xiàn)在仍在應(yīng)用之中，可以與其他方法如動態(tài)規(guī)劃法等結(jié)合使用[4]。

3.2 數(shù)學(xué)優(yōu)化算法

3.2.1 動態(tài)規(guī)劃法

動態(tài)規(guī)劃法(Dynamic Programming，DP)是一種求解多階段決策問題的優(yōu)化方法。用動態(tài)規(guī)劃法求解機組組合問題時，將調(diào)度周期分為若干個調(diào)度時刻，每個時刻即是動態(tài)規(guī)劃法的一個決策階段，各階段的狀態(tài)即為所有機組可能的開停機狀態(tài)組合。從初始時刻開始從前向后計算到達(dá)各階段各狀態(tài)的累計費用，直至最后階段，再從最后階段累計費用最小的狀態(tài)開始，由后向前追朔，依次找到使該費用最小的各階段的狀態(tài)，這樣就可得到最優(yōu)開停機方案。該方法能求得小規(guī)模機組組合問題的最優(yōu)解，但隨著機組數(shù)目及調(diào)度時刻數(shù)的增加，該方法的計算時間會呈指數(shù)形式增長，最終可能導(dǎo)致“維數(shù)災(zāi)”問題的出現(xiàn)。

3.2.2 拉格朗日松弛算法

拉格朗日松弛算法(Lagrangian Relaxation，LR)的思想是把系統(tǒng)約束條件，如負(fù)荷備用，旋轉(zhuǎn)備用等約束，以懲罰項的形式加入目標(biāo)函數(shù)進(jìn)行松弛，把約束條件進(jìn)行松弛后，再將機組組合問題分解為一系列單機子問題和對偶問題。單機子問題采用動態(tài)規(guī)劃法求解，對偶問題采用次梯度法求解。

該方法能有效地處理機組組合問題中較為復(fù)雜的約束條件，并且當(dāng)機組數(shù)目增多時，該方法的求解計算量近似線性增長，不存在“維數(shù)災(zāi)”問題，能找到問題的次優(yōu)解。另外，該方法還可以擴(kuò)展到不同類型機組間(如水電機組與火電機組)的混合調(diào)度問題及電力交易的問題。算法的某些因子具有實際的物理、經(jīng)濟(jì)意義，如拉格朗日函數(shù)中與負(fù)荷平衡約束條件有關(guān)的乘子即為系統(tǒng)邊際成本，但是該方法在求解機組組合問題時存在對偶間隙，求解結(jié)果振蕩，難以找到最優(yōu)解。

3.2.3 混合整數(shù)規(guī)劃法

混合整數(shù)規(guī)劃法(Mixed Integer Programming，MIP)是解決變量中既有整數(shù)又有非整數(shù)問題的一類數(shù)學(xué)方法。該類方法中的代表性性方法有如下兩類：

(1)Benders 分解法

該方法將所求問題分解為只含離散變量和只含連續(xù)變量的兩個子問題，通過協(xié)調(diào)因子在這兩個子問題間進(jìn)行循環(huán)迭代，最終求得問題的最優(yōu)解，Benders 分解法是機組組合問題中最早運用的混合整數(shù)規(guī)劃法。

文獻(xiàn)[11]在廣義 Benders 分解算法的基礎(chǔ)上，一方面充分利用研究時段負(fù)荷曲線的特征，將問題進(jìn)行解耦，減小被研究問題的規(guī)模；另一方面，利用 Benders分解算法在混合整數(shù)規(guī)劃中的有效性，使分解后的子問題最小化，可以提高計算效率。

(2)分支定界法

分支定界法(Branch and Bound，BB)的求解過程主要分為以下幾步循環(huán)進(jìn)行。首先，將最優(yōu)解所在的解空間劃分成許多互不相交的子集，并且這些不相交的子集的并集正好是解空間。第二步，如果其中某個子集中的所有變量的取值都違反了所求優(yōu)化問題的限制條件，那么證明該子集不符合要求，在下一步求解中可以不予考慮。第三步，計算目標(biāo)函數(shù)值的上界。第四步，當(dāng)每個子集的決策變量值未違反限制條件時，計算目標(biāo)函數(shù)值的下界。如果某個最優(yōu)化問題子集的下界超過上界，那么最優(yōu)解肯定不在這個子集中，則剔除該子集。此過程一直繼續(xù)到只有一個子集保留下來。

分支定界法通過對子集的逐步分析來決定子集是否保留，可以提高計算效率，該方法直接求解待求的數(shù)學(xué)問題，理論上能找到全局最優(yōu)解，但由于該方法的復(fù)雜性，使得其計算量太大，實用性不強。

3.3 智能優(yōu)化算法

3.3.1 遺傳算法

遺傳算法(Genetic Algorithms，GA)是一種模擬生物進(jìn)化過程的概率搜索算法，在機組組合問題的求解中得到了越來越多的應(yīng)用并取得了良好的效果。該方法采用并行搜索的方式，能產(chǎn)生多個近最優(yōu)解，由于該算法能處理以懲罰項的形式表示的各種復(fù)雜的約束條件，使得該算法應(yīng)用廣泛，但是該方法的計算效率依賴于參數(shù)的選取，如果參數(shù)選擇不當(dāng)，將會導(dǎo)致計算時間劇增。該算法也是一種隨機搜索算法，無法保證每次求解都能得到全局最優(yōu)解，因此，一般需多次運行求解并從中得到最優(yōu)解或次優(yōu)解。文獻(xiàn)[14]采用改進(jìn)遺傳算法求解建立在情景分析基礎(chǔ)上的隨機機組組合問題，使遺傳算法在機組組合求解問題的應(yīng)用中得到了進(jìn)一步的發(fā)展。

3.3.2 模擬退火算法

模擬退火算法(Simulated Annealing，SA)來源于固體退火原理，將固體加溫至充分高，再讓其徐徐冷卻，加溫時，固體內(nèi)部粒子隨溫度升高變?yōu)闊o序狀，內(nèi)能增大，而徐徐冷卻時粒子漸趨有序，在每個溫度都達(dá)到平衡態(tài)，最后在常溫時達(dá)到基態(tài)，內(nèi)能減為最小。用固體退火模擬組合優(yōu)化問題，將內(nèi)能E模擬為目標(biāo)函數(shù)值f，溫度T演化成控制參數(shù)t，即得到解組合優(yōu)化問題的模擬退火算法。該方法計算速度快，能處理復(fù)雜約束，應(yīng)用廣泛，但是其參數(shù)的選取對計算時間影響很大，到目前為止，尚沒有明確的標(biāo)準(zhǔn)。

3.3.3 蟻群優(yōu)化算法

蟻群優(yōu)化算法(Ant Colony Optimization，ACO)產(chǎn)生于對蟻群行為的研究，蟻群中的螞蟻以“信息素”為通信媒介，間接異步地相互聯(lián)系，這是蟻群優(yōu)化算法最大的特點。螞蟻每次在尋找食物或者在回巢的途徑中，會在經(jīng)過的地方留下一些稱之為“信息素”的化學(xué)物質(zhì)。這些化學(xué)物質(zhì)能被蟻群中下一批尋找食物或返巢的螞蟻感受到，并且對后來螞蟻的運動行為有指導(dǎo)意義，如此一來，當(dāng)路徑上留下的信息素越多時，螞蟻選擇這條路徑的概率也就越大，導(dǎo)致這條路徑上的信息素進(jìn)一步加強，從而形成一種正反饋過程，最后，這種作用的結(jié)果就會持續(xù)到螞蟻找到最短的路徑為止。國內(nèi)外研究表明蟻群算法在解決組合問題時有其特有的優(yōu)越性。

文獻(xiàn)[15]提出的多種群混沌蟻群算法在基本蟻群算法的基礎(chǔ)上，把蟻群分為搜索蟻、偵察蟻和工蟻，并引入了混沌量。一方面繼承了蟻群算法在解決組合問題上的優(yōu)越性；另一方面最大限度地克服了蟻群算法本身的運算速度慢、易陷入局部最優(yōu)等缺點。

3.3.4 粒子群算法

粒子群算法(Particle Swarm Optimization，PSO)是群集智能的代表性方法之一。1995年由Eberhart 博士和kennedy 博士提出，源于對鳥群捕食的行為研究。該算法最初是受到飛鳥集群活動的規(guī)律性啟發(fā)，進(jìn)而利用群體智能建立的一個簡化模型，粒子群算法在對動物集群活動行為觀察基礎(chǔ)上，利用群體中的個體對信息的共享使整個群體的運動在問題求解空間中產(chǎn)生從無序到有序的演化過程，從而獲得最優(yōu)解。粒子群算法被應(yīng)用于機組組合問題求解，研究者們正在對此做更深入的研究。文獻(xiàn)[16]提出一種解決機組組合問題的改進(jìn)雙重 PSO 算法。其中離散 PSO 算法用于確定機組啟停狀態(tài)組合，連續(xù) PSO 算法嵌套入離散PSO 算法當(dāng)中為之進(jìn)化提供方向，并在啟停狀態(tài)確定后用于計算機組出力的經(jīng)濟(jì)分配，為了更快地接近全局最優(yōu)解和防止陷入局部收斂，對算法進(jìn)行了多項改進(jìn)。

3.3.5 免疫算法

免疫算法(Immune Algorithm，IA)模擬了生物免疫系統(tǒng)，是一個具有記憶機制、調(diào)節(jié)機制、評價機制和有導(dǎo)向性地產(chǎn)生某種特異性抗體等特點的算法。由于是多點并行計算，并且通過記憶庫保留優(yōu)秀解，免疫算法能夠有效避免早熟陷入局部最優(yōu)，求解效率高。文獻(xiàn)[17]提出了一種改進(jìn)的免疫算法用于機組組合優(yōu)化，該算法便于考慮不同類型機組啟停的特性，采用抗體片段表示不同的機組組合狀態(tài)，并構(gòu)造了由同一機組的抗體片段集合形成的抗體片段記憶庫，加快了滿足抗原匹配要求的抗體的形成速度。

3.3.6 人工神經(jīng)網(wǎng)絡(luò)算法

人工神經(jīng)網(wǎng)絡(luò)法(Artificial Neural Networks，ANN)是對人腦或自然神經(jīng)網(wǎng)絡(luò)若干基本特性的抽象與模擬，它以大腦的生理研究成果為基礎(chǔ)，其目的在于模擬大腦的某些機理與機制，實現(xiàn)某個方面的功能。目前，常用的兩種神經(jīng)網(wǎng)絡(luò)模型是 BP 網(wǎng)絡(luò)模型和 Hopfield 網(wǎng)絡(luò)模型。人工神經(jīng)網(wǎng)絡(luò)法可以用來求解機組組合等優(yōu)化問題，該方法的優(yōu)點是并行處理能力和在線處理能力強，適合實時控制；缺點是合適的隱層數(shù)目和節(jié)點數(shù)目的確定比較困難，建立人工神經(jīng)網(wǎng)絡(luò)需要的數(shù)據(jù)量很大，訓(xùn)練神經(jīng)網(wǎng)絡(luò)需要的時間較長，算法易陷入局部極值。

4 有待進(jìn)一步研究的內(nèi)容

機組組合問題是電力系統(tǒng)優(yōu)化運行的重要組成部分，幾十年來，機組組合問題一直是電力系統(tǒng)研究中的熱點和難點，為了適應(yīng)未來電力系統(tǒng)的節(jié)能發(fā)電的推廣實施及智能電網(wǎng)的實現(xiàn)，還有待研究如下幾方面的內(nèi)容：

(1)目前，針對機組組合優(yōu)化求解的問題，仍然沒有一種快速精確的求解算法能滿足實際工程的需求，機組組合問題的大規(guī)模、非線性、高維及非凸等特性給求解算法的尋找?guī)砹撕艽罄щy，仍需研究者們做進(jìn)一步尋找和探究。

(2)傳統(tǒng)的機組組合模型中考慮了諸如功率平衡、機組爬坡能力、開停機時間等約束條件，但實際問題中存在一些不確定因素，需考慮更全面的安全網(wǎng)絡(luò)約束，在國外，安全網(wǎng)絡(luò)約束通常是指同時包含基態(tài)和預(yù)想故障下的網(wǎng)絡(luò)約束[18]，而在國內(nèi)，“安全“通常只包含基態(tài)的網(wǎng)絡(luò)約束，這一點是我們今后需要做出改善并繼續(xù)研究的內(nèi)容[19]。

5 總結(jié)

本文全面總結(jié)了傳統(tǒng)機組組合數(shù)學(xué)模型及其求解方法，分析比較了各種求解方法的優(yōu)缺點，并在此基礎(chǔ)上介紹了近年來機組組合模型考慮到的一些新的約束條件，總結(jié)了近年來基于市場、節(jié)能等因素用于機組組合問題求解的新型智能優(yōu)化算法，綜述了機組組合問題的發(fā)展和應(yīng)用現(xiàn)狀，并展望了未來有待進(jìn)一步研究的內(nèi)容。

[1] 李文沅.電力系統(tǒng)安全經(jīng)濟(jì)運行[J].模型與方法,1988(32):1-7.

[2] 汪洋，夏清，康重慶.機組組合算法中起作用整數(shù)變量的辨識方法[J].中國電機工程學(xué)報，2010，30(13)：46-52.

[3] 黎靜華，蘭飛.機組組合問題的模型及算法綜述[J].現(xiàn)代電力學(xué)報，2011.

[4] 陳皓勇，王錫凡.機組組合問題的優(yōu)化方法綜述[J].電力系統(tǒng)自動化，1999，23(5)：51-56.

[5] Padhy N P.Unit commitment problem under deregulatedenvironment-a review[C]//Proceedings of IEEE Power &Energy Society General Meeting.Toronto：IEEE Power &Energy Society，2003：1088-1094.

[6] Padhy N P.Unit commitment：a bibliographical survey[J].IEEE Trans.on Power Systems，2004，19(2)：1196-1205.

[7] Pinto H，Magnago F，Brignone S，et al . Security constrained unit commitment：network modeling andsolution issues[C]//Proceedings of IEEE PSCEConference.Atlanta：IEEE Power & Energy Society，2006：1759-1766.

[8] 李曉磊，周京陽，于爾鏗，等.電力系統(tǒng)機組組合研究綜述[C]//中國高等學(xué)校電力系統(tǒng)及其自動化專業(yè)第二十四屆學(xué)術(shù)年會論文集(上冊).北京：中國農(nóng)業(yè)大學(xué)，2008：803-807.

[9] 李整，譚文，秦金磊.一種用于機組組合問題的改進(jìn)雙重粒子群算法[J].中國電機工程學(xué)報，2012,9:80-86.

[10] 李茜，劉天琪，王福軍，等.機組組合在含風(fēng)電設(shè)備的備用協(xié)調(diào)優(yōu)化[J].東北電力,2003,41(7):1481-1484.

[11] 夏清，鐘海旺，康重慶.安全約束機組組合理論與應(yīng)用的發(fā)展和展望[J].中國電機工程學(xué)報,2013,33(16):94-103.

[12] 康重慶，陳啟鑫，夏清.低碳電力技術(shù)的研究展望[J].電網(wǎng)技術(shù)，2009，33(2)：1-7.

[13] Hara K,Kimura,Honda N.A Method for Planning Economic Unit Commitment and Maintenance of Thermal Power Systems[J].IEEE Trans on Power Apparatus and Systems,1966,PAS-85(5):427-436.

[14] 熊高峰，聶坤凱，劉喜蘋，等.基于遺傳算法的隨機機組組合問題求解[J].電力系統(tǒng)及其自動化,2012,24(5):93-99.

[15] 李整，譚文，秦金磊.一種用于機組組合問題的改進(jìn)雙重粒子群算法[J].中國電機工程學(xué)報,2012,32(25):189-195.

[16] 王敏蔚，楊莉.采用改進(jìn)免疫算法的機組組合優(yōu)化[J].電網(wǎng)技術(shù)，2010，34(8)：112-117.

[17] Pinto H，Magnago F，Brignone S，et al . Security constrained unit commitment：network modeling andsolution issues[C]//Proceedings of IEEE PSCEConference.Atlanta：IEEE Power & Energy Society，2006：1759-1766.

[18] 汪洋，夏清，康重慶.考慮電網(wǎng) N-1 閉環(huán)安全校核的最優(yōu)安全發(fā)電計劃[J].中國電機工程學(xué)報，2011，31(10)：39-45.

[19] 張利，趙建國，韓學(xué)山.考慮網(wǎng)絡(luò)安全約束的機組組合新算法[J].電網(wǎng)技術(shù)，2006，30(21)：50-55.

A Summary of Electric Power System Unit Combination Proplem

LIUYan-fang,XIAChang-hao

(Electrical and New Energy College,Sanxia University,Yichang 443000,China)

The unit combination problem is an important part of the optimal operation of the electric power system and it always hot spots and difficult points of the electric power system study.The paper sums up the mathemational model and classical solving method of traditional unit combination.On the basis of this,present new intelligent optimal algorithm used for the unit combination problem and look forward to future study.

unit combination;heuristic approach;optimal alogrithm of maths;intelligent optimal alogrithm

1004-289X(2015)03-0005-05

TM71

B

2014-03-06