波致海底緩傾角無限坡滑動穩定性計算分析探討

劉小麗，竇錦鐘，英姿，霍沿東，張旭

（1.中國海洋大學環境科學與工程學院，山東青島 266100；2.海洋環境與生態教育部重點實驗室，山東青島 266100）

波致海底緩傾角無限坡滑動穩定性計算分析探討

劉小麗1，2，竇錦鐘1，英姿1，霍沿東1，張旭1

（1.中國海洋大學環境科學與工程學院，山東青島 266100；2.海洋環境與生態教育部重點實驗室，山東青島 266100）

波浪作用下海底無限坡滑動穩定性計算的極限平衡法中，忽略了坡體水平向應力狀態的影響，為此，針對波浪作用下海底緩傾角無限邊坡的特點，提出直接基于滑動面處土體應力狀態的滑動穩定性計算方法（簡稱應力狀態法），并分析了其適用范圍。對具體算例的分析表明，應力狀態法計算得出的安全系數大于極限平衡法的安全系數，且隨著滑動面深度的增加、土體泊松比以及邊坡坡角的增大，兩種計算方法得出的安全系數的差異會逐漸增大；對于波浪作用下的海底緩傾角無限邊坡，在失穩時極可能沿具有一定厚度的滑動帶而不是單一的滑動面而滑動，且波致最大剪應力所在的深度，常常不是斜坡體最易失穩滑移的深度。

海底無限邊坡；波浪；穩定性分析；緩傾角

1 引言

與陸地上的滑坡相比，海底滑坡的最顯著特征之一，是大部分的海底滑坡發生在非常平緩的斜坡上［1］。如位于挪威海域的Storegga滑坡［2］是迄今發現的最大的海底復合滑坡體，其滑坡區西南部坡角1.17°～1.32°，東部坡角0.55°～1.14°；南海北部陸坡區有較多滑坡發育的跡象，其東部的臺灣淺灘陸坡段，總體坡度約為3.4°，珠江海谷段陸坡的下陸坡相對陡峭處的坡度為3°左右［3］；楊作升等［4］對黃河口水下滑坡體系的特征及其相互作用進行了分析，指出廢棄的1964－1976年的黃河口沙嘴水下底坡的中上部坡度相對較陡，但其平均坡度不超過0.5°。

除重力作用外，沉積物快速沉積導致的超高孔隙水壓力、淺層氣的存在、地震以及波浪作用等因素都有可能誘發海底緩傾角滑坡，如甘華陽等［5］介紹了海底天然氣水合物分解導致滑坡的機制及該種海底滑坡體的特征；張亮和欒錫武［3］對南海北部陸坡的穩定性進行了詳細定量分析研究，認為地震是引發南海北部滑坡最主要的觸發機制之一。波浪是近岸及淺水區海底斜坡穩定性分析中需要考慮的一個重要因素，Henkel［6］通過計算分析認為在密西西比河口波浪能引起120 m深度處海底軟土斜坡的破壞。波浪一般所影響的水深相當于波長的一半，當水深小于1／2波長時，波長變短、波高變大，并最終出現翻卷形成破波［7］。

Henkel［6］采用圓弧形滑動面通過力矩平衡分析了波浪對海底斜坡穩定性的影響，Wright和Dunham［8］利用有限元分析了無限坡滑動模式下波浪對海底斜坡的作用。對于海底緩傾角斜坡，大部分文獻將其視為無限坡模式利用極限平衡法進行了穩定性分析［2—3，9—12］。無限坡滑動模式是一種較簡單的邊坡穩定性分析模型，通常當斜坡滑動面為平行于坡面的平面（沿滑動方向的傾角為常數），且滑坡體的厚度遠小于其滑動方向的長度（一般滑坡體的長度與厚度之比大于10）時，可將其作為無限坡進行分析［12—13］。

在波浪導致海底無限坡滑動穩定性計算中，常采用極限平衡法對單位寬度的條塊進行受力分析，將波浪產生的最大剪切應力作為下滑應力作用于條塊底部［1，13］，條塊的重力則分解為平行于滑動面的下滑力和垂直于滑動面的壓力，與傳統的條分法處理方式相同，這種方法只考慮了坡體重力產生的豎向應力作用，而忽略了土體水平向應力的影響［14］，這是目前海底斜坡穩定性極限平衡法分析中普遍存在的問題［2，9—12］。

對于海底緩傾角邊坡，因其坡度較小，重力作用下土體的水平向應力場可近似通過靜止側壓力系數進行計算［14］。在波浪導致海底緩傾角無限邊坡的穩定性分析中，除了需要考慮波浪產生的最大剪切應力外，是否需要考慮坡體中的水平向應力，其對穩定性分析結果的影響如何，目前的文獻中尚未見分析。本文在波浪作用下海底緩傾角無限坡穩定性分析的極限平衡法基礎上，提出基于坡體應力狀態進行穩定性分析的方法（應力狀態法），并對該方法的適用性進行了分析，通過具體算例對極限平衡法和應力狀態法的計算結果進行了對比，對波致海底緩傾角無限坡的滑動失穩特征進行了探討。

2 波致海底無限坡穩定分析的極限平衡法

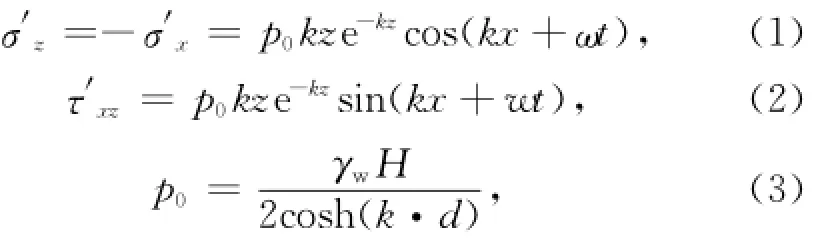
將海床視為均質多孔彈性介質，海床內的滲流符合Darcy定律，波浪作用下海床的應力變形滿足Biot固結方程，波浪為線性波條件下，根據Yamamoto［15］的理論分析，可得無限深海床應力場的簡化計算公式為：式中，σ′z、σ′x、τ′xz分別為海床面以下某深度處土體的波致豎向正應力、水平向正應力及波致剪切應力，p0是海床表面波浪壓力（波底壓力）幅值，k＝2π／L為波數，L為波長，γw為水的容重，z為海床面以下的深度坐標，x為水平向坐標，ω為波浪角頻率，H為波高，d為水深。從式（2）可知，海床面以下某深度z處的波致最大剪應力為τ′xz－m＝p0kze－kz。

在波浪循環荷載作用下，不考慮孔隙水壓力的累積效應，在波峰和波谷處分別出現最大豎向正應力和最大水平向正應力；在波節點處剪切應力最大，而水平正應力和豎向正應力為零。

對于海底無限坡的穩定性計算，除了利用有限元進行應力變形分析外［8］，一般采用簡單的極限平衡法［2，9—12］，取單位寬度的土體條塊進行受力平衡分析。如圖1所示，波浪作用下，取位于波節點位置的土條進行受力分析，土條底部的下滑力由兩部分組成［1，13］，一部分為波浪在滑面處產生的最大剪切應力形成的下滑力Tw，另一部分是重力在滑動方向的下滑力分量Gt，則總的下滑力為：

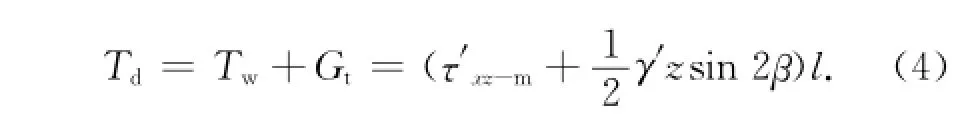
土條的抗滑力為R，在總應力法分析中，R＝Cul，Cu為土體的不排水抗剪強度；在有效應力法的分析中，由于重力在垂直滑面方向的壓力分量為Gn＝γ′zlcos2β，則抗滑力根據Mohr-Coulomb抗剪強度公式進行計算，其值為R＝（c′＋γ′zcos2βtanφ′）l。

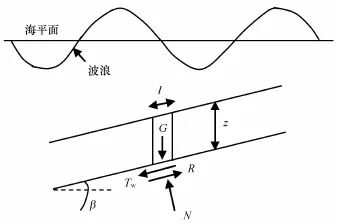
圖1 波致海底無限坡極限平衡法計算示意圖Fig.1 Sketch of wave-induced stability analysis on submarine infinite slopes by limit equilibrium method

因此，極限平衡法計算中，總應力分析時安全系數的表達式為：

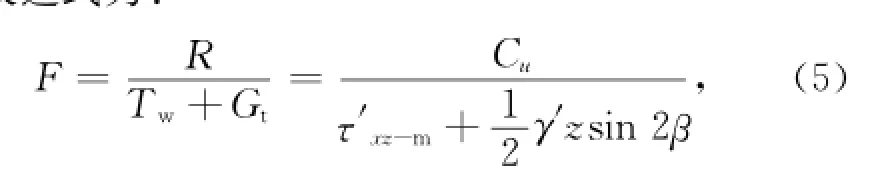
有效應力分析時安全系數的表達式為：

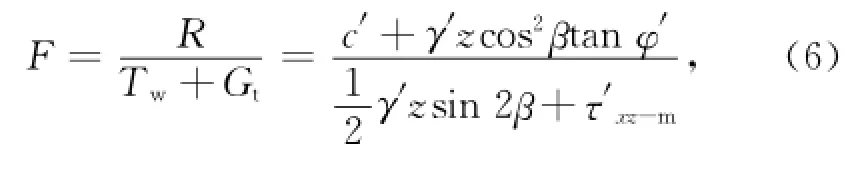
式中，γ′為斜坡土體的有效容重，c′和φ′分別為斜坡土體的有效黏聚力和有效內摩擦角。

波浪作用下海底無限坡穩定性計算的極限平衡法中，考慮了坡體相應位置的豎向應力（重力產生的豎向應力場），而沒有考慮與之對應的水平向應力［14］。波浪作用下海底無限坡穩定性計算中由于是對波節點位置的土條進行受力平衡分析，而波節點處波浪產生的剪切應力最大，水平向正應力和豎向正應力均為零，因此，波節點處土體水平向正應力主要是坡體重力作用引起的。

3 基于坡體應力狀態的穩定性計算方法

3.1 穩定性分析思路與計算公式

如上所述，極限平衡法中未考慮土體水平向應力對穩定性分析的影響，對于海底緩傾角斜坡，重力作用下坡體水平向應力場可通過土體的靜止側壓力系數K0進行近似計算［14］。

緩傾角斜坡自重作用下某深度處的水平向有效應力可近似計算為：

式中，K0為土體靜止側壓力系數，與土體泊松比v有關，根據彈性理論

土體靜止側壓力系數K0的范圍一般為0.4～1.0［15］。

在海底無限坡穩定性計算的極限平衡法基礎上，基于坡體的應力狀態，即同時考慮坡體水平向應力和豎向應力的影響，并結合波浪導致的最大剪切應力，根據滑面處土體的應力平衡條件計算沿滑面的切向下滑應力及垂直滑面的正應力，并在此基礎上計算坡體的安全系數，這種基于坡體應力狀態進行穩定性分析的方法，此處稱為“應力狀態法”，其具體計算公式如下。

設海底緩傾角無限坡的坡角為β，坡體重力作用下的水平向有效正應力通過K0計算，在波節點位置，根據滑面處微元體的應力平衡條件，可得平行于滑面的下滑應力τ及垂直于滑面的正應力σ′分別為：

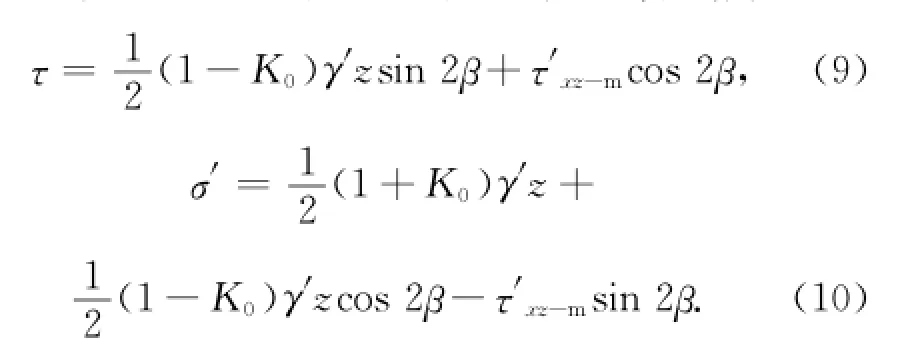
故應力狀態法計算中，總應力分析時安全系數的表達式為：

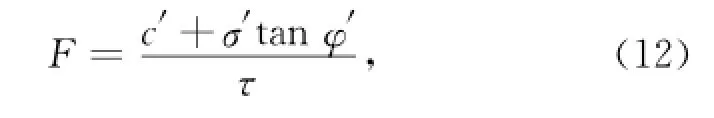
τ和σ′的計算分別如式（9）和式（10）中所示。

對比波浪作用下海底無限坡滑動穩定性分析的極限平衡法安全系數計算公式，可發現兩種穩定性分析方法中，其安全系數最終計算表達式物理意義的實質是相同的，即二者都是滑動面上波致最大剪應力位置處坡體抗滑應力與下滑應力的比值，只是坡體應力的計算方法有所不同，極限平衡法是基于不變形體的受力平衡進行下滑力和抗滑力的計算，忽略了坡體水平向外力的作用，由此得到的安全系數表達式中只包含了坡體豎向應力分量和波致剪應力的影響；而應力狀態法則是直接基于外力作用下變形體的應力計算結果，根據坡體的應力平衡條件進行下滑力和抗滑力的計算，其安全系數表達式中不僅包含坡體豎向應力分量和波致剪應力，還包含水平向應力分量的影響。

綜上，無論是極限平衡法還是應力狀態法，二者在分析波致海底緩傾角無限邊坡滑動穩定性時，其安全系數計算式均體現為應力表達的抗滑力與下滑力的比值，兩種方法安全系數所表達的物理意義是相同的；且應力狀態法的計算是基于變形體的應力分析，更符合坡體的實際物理狀態，因此，將該方法用于波致海底緩傾角無限坡的滑動穩定性計算是可行的。

3.2 應力狀態法的適用范圍

由應力狀態法計算公式可知，坡體水平向正應力是通過土體的靜止側壓力系數K0計算得到的，當坡角為零時，根據彈性理論該計算是正確的，但隨著邊坡坡度的增加（坡角的增大），通過K0計算得到的坡體水平向應力場與其實際的應力狀態相差會逐漸增大，故應力狀態法的可靠度在較大程度上依賴于對坡體水平向應力場計算的準確度，亦即其適用范圍與坡角密切相關。

為了分析應力狀態法適用的坡角范圍，將坡體視為彈性介質，利用Sigma／W有限元軟件［16］計算重力作用下無限坡的應力場（可視為實際應力場），并將其與利用K0計算得到的坡體水平向應力場進行比較，分析計算誤差。

如圖2所示為有限元計算的幾何模型，邊坡水平向長400 m，坡腳處土體厚度20 m，坡頂處的厚度依

有效應力分析時安全系數的表達式為：據坡度的不同而變化。計算分析了坡角β為3°、4°和6°時的邊坡應力場，與傾角為0°時的邊坡應力場相比，坡體的豎向應力場變化很小，水平向應力場依據坡角的不同，在不同的深度范圍內有一定變化。總體而言，與K0計算的坡體水平應力相比，靠近坡腳附近的水平應力場偏大，而靠近坡頂附近的水平應力場偏小，考慮到此處分析的無限坡的性質，取水平方向坡體中間位置處的截面（如圖2中的A－A截面）進行水平應力的計算誤差分析，結果如表1所示。

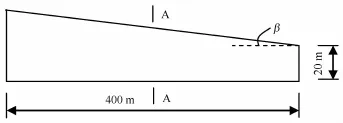
圖2 有限元計算的幾何模型Fig.2 Geometric model for finite element analysis

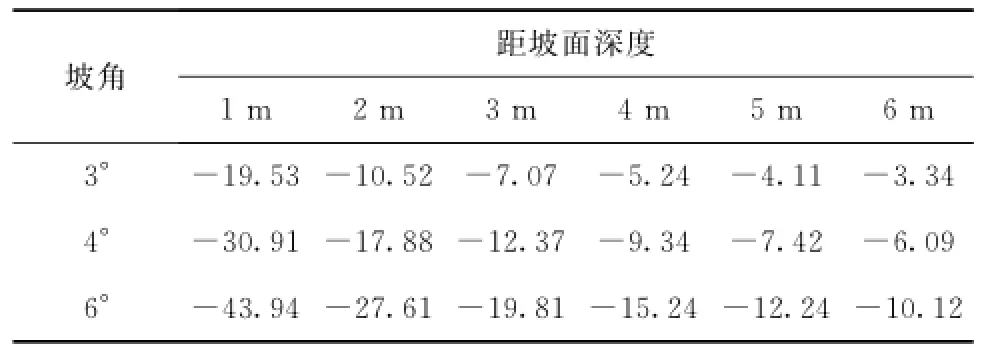
表1 水平應力計算誤差（單位：%）Tab.1 Error analysis of horizontal stress（unit：%）

因坡體中部A－A截面利用K0計算出的水平應力數值小于實際的水平應力，因此表1中的誤差百分數為負值。從表1中數值可知，應力狀態法的適用坡角與潛在滑動面深度有關，如果以水平應力計算誤差10%為判斷標準（由此引起的安全系數的計算誤差分析見后述4.3節內容），則當滑動面深度大于5 m時，其適用的坡角范圍為0°～6°；滑動面深度3～5 m時，其適用坡角范圍為0°～4°；滑動面深度2～3 m時，其適用坡角為0°～3°。

4 算例分析與討論

分別利用極限平衡法與本文提出的應力狀態法，通過某具體算例，從海底緩傾角無限坡的穩定性隨滑動面深度的變化特征、土體泊松比和斜坡坡度對穩定性計算結果的影響等方面，對波致海底緩傾角無限坡滑動穩定性的計算方法進行對比分析，同時對波浪作用下海底緩傾角無限坡的失穩滑動特征進行探討。

某海底緩傾角無限邊坡，坡角β＝1.8°，土體浮容重γ′＝9.4 kN／m3，剪切模量G＝3.5×106Pa，泊松比ν＝0.35，有效黏聚力c′＝1.8 kPa，有效內摩擦角φ′＝6°；波浪參數為波高5.2 m、周期8.6 s、水深8 m，對應的波長70.6 m。

4.1 波致海底緩傾角無限坡穩定性隨深度的變化特征

基于前述波致剪應力的表達式，在0.159L深度處剪應力達最大值，其值為0.368P0。此處算例中波長L為70.6 m，最大波致剪應力發生在11 m深度處，為此，對距坡面0.5～13 m深度范圍內的坡體穩定性及其隨深度的變化特征進行分析。

如圖3所示為坡體安全系數隨潛在滑動面深度的變化曲線，可以看出，應力狀態法計算的安全系數大于極限平衡法的計算結果，且隨著潛在滑動面深度的增加，兩種計算方法所得安全系數的差值也在逐漸增加，在深度4 m處二者相差11%，在13 m位置處達22%。

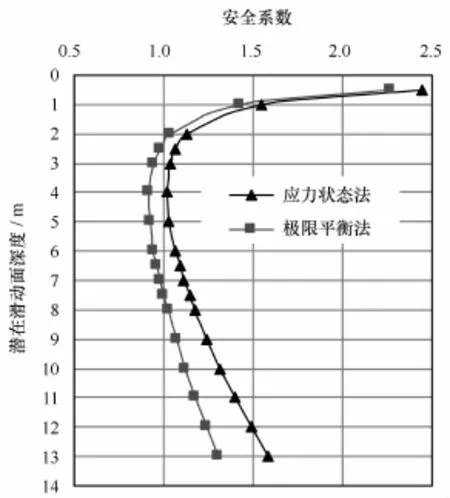
圖3 安全系數隨滑動面深度的變化Fig.3 Variations of safety factor with different depths of slip surface

根據兩種安全系數計算方法的表達式可知，應力狀態法考慮了坡體水平向應力場的影響，由于該應力場是重力引起的水平向壓應力場，而水平壓力場對坡體的橫向滑動變形具有一定的約束作用，因此在應力狀態法安全系數計算表達式中，水平向應力的出現明顯減小了沿滑面的下滑力，其計算所得的安全系數較極限平衡法偏大，且隨著滑面計算深度的增加，水平向應力場逐漸增大，其對坡體滑動變形的約束效應也逐漸增加，導致隨著深度增加兩種方法計算結果的差異逐漸增大。

兩種計算方法所得安全系數均隨滑面深度的增加出現先減小后增大的變化趨勢，在距坡面4 m深度處安全系數達最小值，此時極限平衡法計算的安全系數為0.92，應力狀態法的安全系數為1.02，表明斜坡最易在該深度處發生失穩滑動。對安全系數隨深度的變化數值進行分析可知，在距坡面3～6 m的深度范圍內，該斜坡滑動穩定系數的數值非常接近且都相對較小，基本都處于最危險滑動區域，因此斜坡體極有可能沿具有一定厚度的滑動帶失穩滑動，而不只是沿單一的滑動面發生滑動。

本例中最大波致剪切應力發生在距坡面11 m的深度處，而穩定性計算結果表明，最易滑移的位置發生在距坡面3～6 m的深度范圍，遠小于最大波致剪應力的深度位置，這是因為隨著深度的增加，斜坡土體的抗剪能力也在逐漸增大，在有效應力分析中體現在斜坡滑動面上的有效正應力隨著深度增加而增大，進而增大了抗剪強度；而在總應力分析中，斜坡土體的不排水抗剪強度一般會隨著深度的增加而增大［6，11—12］，故波致剪應力最大的深度位置往往不是斜坡體最易失穩滑移的位置。

4.2 泊松比對波致海底緩傾角無限坡穩定性計算的影響

以滑動面的深度4 m為例（該位置處的坡體安全系數最小），繪制海底緩傾角無限坡安全系數隨土體泊松比的變化曲線，如圖4所示。

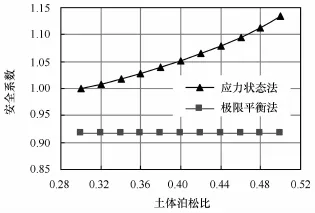
圖4 安全系數隨土體泊松比的變化Fig.4 Variations of safety factor with different Poisson ratios of soil

從圖4中可以看出，極限平衡法中因沒有考慮重力引起的水平向應力作用，其計算出的安全系數是一個常值0.92，不隨泊松比變化。應力狀態法中考慮了水平向應力作用，且該水平應力的數值直接受泊松比的影響，因此，應力狀態法計算的坡體安全系數隨著泊松比的變化而有較明顯的改變，當泊松比為0.3時，其安全系數為1.00，與極限平衡法所得安全系數相差9%，當泊松比為0.5時，其安全系數為1.13，與極限平衡法的安全系數相差達23%。

從應力狀態法的安全系數計算公式可以看出，當泊松比較小時，坡體水平向壓應力的影響相對減弱，由此導致水平向壓應力場對坡體滑動變形的約束作用隨之降低，其安全系數計算結果與極限平衡法的計算結果就越相近，故泊松比越小，兩種方法的計算結果相差越小；反之則相差越大。

4.3 坡度對波致海底緩傾角無限坡穩定性計算的影響

改變海底斜坡的坡度，分析坡度的變化對兩種穩定性分析方法計算結果的影響。以滑動面深度4 m為例進行分析，則根據前述應力狀態法適用范圍的分析結果，選取坡角變化范圍0.3°～4.0°，計算結果如圖5所示。

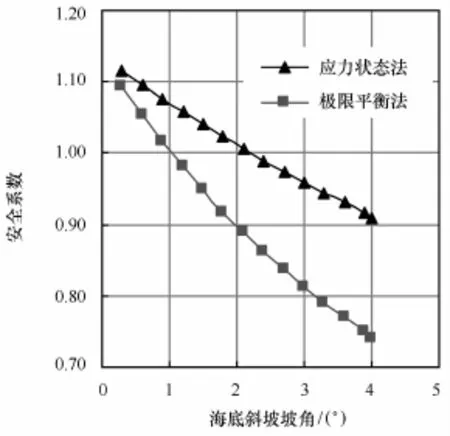
圖5 安全系數隨坡角的變化Fig.5 Variations of safety factor with different slope angles

根據圖5可知，隨著坡角的增大，兩種計算方法所得安全系數的差異逐漸增大，當坡角為1.8°時，相差11%，而當坡角為4.0°時相差22%。隨著坡角的增大，重力對坡體穩定性計算結果的影響逐漸增加，進一步由重力作用導致的水平向壓應力場對坡體滑動變形的約束效應相對隨之增強，應力狀態法計算中考慮了水平向應力場的這種作用，而極限平衡法沒有考慮，故導致隨著坡角的增加，兩種穩定性分析方法計算結果之間的差異隨之增大。

如前所述，應力狀態法計算穩定性時的坡角適用范圍，是以K0計算的坡體水平應力與實際水平應力相差不大于10%為判斷標準而得出的，則當水平應力計算誤差為10%時，其對應的安全系數的誤差是否可以接受，此處將通過算例進行分析。

以海底無限坡坡角4°為例，當潛在滑動面深度為4 m時，利用K0計算坡體水平應力，此時應力狀態法計算得到的安全系數為0.91；當坡體的實際水平應力與利用K0計算得到的水平應力相差10%時，利用坡體實際水平應力計算得到的安全系數為0.93，與直接利用K0計算得到的安全系數相差2%，誤差較小。上述分析表明，當K0計算的坡體水平應力與實際水平應力相差不超過10%時，對坡體安全系數計算的影響較小，其誤差是可以接受的。

5 結論

對目前波致海底無限坡滑動穩定性計算的極限平衡法中存在的問題進行了分析，并在此基礎上，提出了基于坡體應力狀態的穩定性計算方法（應力狀態法）及其適用范圍，通過具體算例，對極限平衡法和應力狀態法的計算結果進行了分析對比，對波致海底緩傾角無限坡的滑動失穩特征進行了探討，主要得到了以下結論。

（1）提出了波浪作用下海底緩傾角無限坡滑動穩定性分析的應力狀態法，并分析了其適用范圍；

（2）應力狀態法計算的安全系數大于極限平衡法的安全系數，且隨著滑動面深度的增加、土體泊松比以及邊坡坡角的增大，兩種計算方法得出的安全系數的差異逐漸增大；

（3）對于海底緩傾角無限邊坡，在波浪作用下失穩時，極有可能沿具有一定厚度的滑動帶失穩滑動，而不只是沿著單一的滑動面滑動；

（4）對于波浪作用下的海底緩傾角無限邊坡，由于坡體抗剪強度的影響，波致最大剪應力所在的深度位置，常常不是斜坡體最易失穩滑移的位置。

［1］ 葉銀燦.中國海洋災害地質學［M］.北京：海洋出版社，2012.

Ye Yingcan.Marine hazard geology［M］.Beijing：China Ocean Press，2012.

［2］ Leynaud D，Mienert J，Nadim F.Slope stability assessment of the Helland Hansen area offshore the mid-Norwegian margin［J］.Marine Geology，2004，213（1／4）：457－480.

［3］ 張亮，欒錫武.南海北部陸坡穩定性定量分析［J］.地球物理學進展，2012，27（4）：1443－1453.

Zhang Liang，Luan Xiwu.Quantitative analysis of submarine slope stability on the northern slope of the South China Sea［J］.Progress in Geophsics，2012，27（4）：1443－1453.

［4］ 楊作升，陳衛民，陳彰榕，等.黃河口水下滑坡體系［J］.海洋與湖沼，1994，25（6）：573－581.

Yang Zuosheng，Chen Weimin，Chen Zhangrong，et al.Subaqueous landslide system in the Huanghe River（Yellow River）delta［J］.Oceanologia et Limnologia Sinica，1994，25（6）：573－581.

［5］ 甘華陽，王家生，胡高韋.海洋沉積物中的天然氣水合物與海底滑坡［J］.防災減災工程學報，2004，24（2）：177－181.

Gan Huayang，Wang Jiasheng，Hu Gaowei.Submarine landslide related to natural gas hydrate within benthal deposit［J］.Journal of Disaster Prevention and Mitigation Engineering，2004，24（2）：177－181.

［6］ Henkel D J.The role of waves in causing submarine landslides［J］.Geotechnique，1970，20（1）：75－80.

［7］ 王樹青，梁丙臣.海洋工程波浪力學［M］.青島：中國海洋大學出版社，2013.

Wang Shuqing，Liang Bingchen.Wave mechanics for ocean engineering［M］.Qingdao：China Ocean University Press，2013.

［8］ Wright S G，Dunham R S.Bottom stability under wave induced loading［C］／／Proceeding 4th Annual Offshore Technology Conference，Houston，1972：853－862.

［9］ L'Heureux JS，Vanneste M，Rise L，et al.Stability，mobility and failure mechanism for landslides at the upper continental slopeoff Vesteralen，Norway［J］.Marine Geology，2013，346：192－207.

［10］ Ikari M J，Strasser M，Saffer D M，et al.Submarine landslide potential near the megasplay fault at the Nankai subduction zone［J］.Earth and Planetary Science Letters，2011，312：453－462.

［11］ 顧小蕓.粘質海底穩定性實例分析［J］.工程地質學報，1996，4（1）：32－38.

Gu Xiaoyun.Case study of clayey seabottom stability［J］.Journal of Engineering Geology，1996，4（1）：32－38.

［12］ 葉銀燦，陳錫土，宋連清，等.浙江北部島嶼海域土體穩定性研究［J］.東海海洋，1996，14（1）：1－18.

Ye Yincan，Chen Xitu，Song Lianqing，et al.A study for the seafloor sediment stability around the island areas of northern Zhejiang Province［J］.Donghai Marine Science，1996，14（1）：1－18.

［13］ Hampton M A，Lee H J，Locat J.Submarine landslides［J］.Reviews of Geophysics，1996，34（1）：33－59.

［14］ Lade P V.Static instability and liquefaction of loose fine sandy slopes［J］.Journal of Geotechnical Engineering，1992，118（1）：51－71.

［15］ Yamamoto T.Sea bed instability from waves［C］／／Proceeding 10th Annual Offshore Technology Conference，Houston，1978：1819－1828.

［16］ GEO-SLOPE International Ltd.Stress-deformation modeling with Sigma／W 2007［M］.Canada：GEO-SLOPE International Ltd，2008.

Wave-induced stability analysis on submarine infinite slope with gentle dip angle

Liu Xiaoli1，2，Dou Jinzhong1，Ying Zi1，Huo Yandong1，Zhang Xu1
（1.College of Environmental Science and Engineering，Ocean University of China，Qingdao 266100，China；2.Key Laboratory of Marine Environment and Ecology，Ministry of Education，Qingdao 266100，China）

For wave-induced stability analysis on submarine infinite slopes，the limit equilibrium method generally ignores horizontal stresses acting in the soil deposit.On basis of describing the characteristics of the submarine infinite slope under wave action and considering the soil stress state at the slip surface，this study proposed a stress analysis method to analyze sliding stability of the submarine infinite slope，and discussed the applicable prospect of the method.A case study of a submarine infinite slope has been conducted by both of the limit equilibrium method and the proposed stress analysis method.The results have shown that the factor of safety by the stress analysis method is greater than that of the limit equilibrium method，and the differences of factors obtained by the two methods become larger with increasing depth of the slip surface，Poisson ratio of the soil deposit and dip angle of the infinite slope.For a submarine infinite slope with gentle dip angle under wave action，it may slide along a slip zone rather than a single slip surface under unstable state，and the depth for the maximum shear stress does not generally indicate the most instability location of the infinite slope.

submarine infinite slope；wave action；stability analysis；gentle dip angle

P642.22

A

0253-4193（2015）03-0099-07

劉小麗，竇錦鐘，英姿，等.波致海底緩傾角無限坡滑動穩定性計算分析探討［J］.海洋學報，2015，37（3）：99—105，

10.3969／j.issn.0253-4193.2015.03.010

Liu Xiaoli，Dou Jinzhong，Ying Zi，et al.Wave-induced stability analysis on submarine infinite slopes with gentle dip angle［J］.Haiyang Xuebao，2015，37（3）：99—105，doi：10.3969／j.issn.0253-4193.2015.03.000

2014-05-05；

2014-08-30。

國家自然科學基金項目（41272316）。

劉小麗（1974—），女，山東省青島市人，副教授，主要從事海洋地質災害相關方面的研究。E-mail：LXL4791＠163.com