基于改進型灰色預測模型的SINS/GPS組合導航系統

王立冬，車 琳，魯 軍，高 慶

（1. 軍械工程學院，石家莊 050003；2. 中國華陰兵器試驗中心，華陰 714200）

基于改進型灰色預測模型的SINS/GPS組合導航系統

王立冬1，車 琳2，魯 軍1，高 慶1

（1. 軍械工程學院，石家莊 050003；2. 中國華陰兵器試驗中心，華陰 714200）

針對SINS/GPS組合導航系統中的GPS故障，結合GPS導航定位信息的特點，提出了基于改進型灰色預測的GPS故障預測模型，實現了GPS故障預測；結合SINS/GPS組合導航系統數學模型，進行了基于改進型灰色預測的SINS/GPS組合導航系統仿真。仿真結果表明，GPS位置數據預測殘差小于1.5 m；在GPS短暫故障期間，由預測數據取代GPS故障數據，可以有效提高SINS/GPS組合導航系統的抗干擾能力，保證其導航精度；比較GPS故障數據和預測數據，并根據故障數據的持續時間和變化特點等，可以診斷GPS故障是硬件故障還是外部干擾的影響，有助于實現GPS的故障判別與隔離。

控制與導航；灰色預測模型；故障預測；組合導航

近年來，故障預測與健康管理技術逐漸成為航空航天領域研究的一個熱點。特別是故障預測技術為系統重構爭取了更多時間，提高了系統可靠性。目前，故障檢測、故障診斷和健康管理技術逐漸成熟，但故障預測還處在初步發展階段，仍屬于一大技術難題[1]。

導航與控制部分是各種航天器的關鍵部分，其故障可能造成災難性的后果。如在SINS/GPS（或北斗系統）組合導航系統中，GPS負責提供量測信息，如果這些量測信息出現問題，將使SINS/GPS組合導航系統的誤差逐漸增大，直至使航天器偏離軌道。因此，開展航天器導航與控制部分的自主故障診斷和故障預測技術研究，并將現有其它領域的故障診斷和故障預測的研究成果應用于該系統具有重要的現實與深遠意義。GPS的解析模型比較復雜，一般采用非解析模型的故障預測方法進行故障預測[2]。為此，本文結合GPS導航定位信息的特點，提出了一種基于信號處理-改進型灰色預測模型的GPS故障預測方法對GPS故障進行預測，以提高SINS/GPS組合導航系統的可靠性和導航精度，并進行了仿真研究。

1 改進型灰色預測模型

灰色量的處理過程就是采用數據生成方法來尋求其中規律性的過程。本文利用此規律性來預測未來時刻GPS的定位數據，實現了GPS故障預測。

1.1 灰色預測模型

常用的單序列一階線性灰色模型[3-4]記作GM(1,1)。

① GM(1,1)建模的原始數據序列為

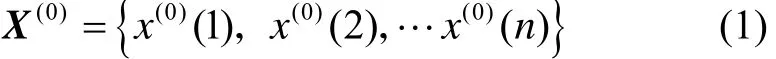
式中：n為數列長度，一般取n≥4。

對原始數據需要進行灰色預測建模可行性的序列級比判斷[5]。

② 利用一次累加生成1-AGO單增序列，設X(1)為X(0)的1-AGO 序列，即

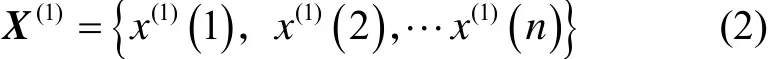
對于非負的數據序列，累加生成可以弱化隨機性，增加規律性，使生成序列呈指數增長規律。

③ 建立GM(1,1)預測模型

設Z(1)為X(1)的緊鄰均值生成序列，即

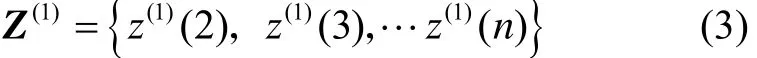
則GM(1,1)的灰色微分方程為

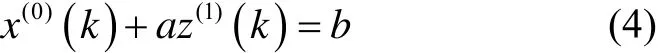
式中：x(0)(k)為灰導數，a為發展系數，z(1)(k)為背景值，b為灰作用量。

以k=2, 3,··,n代入式(6)，寫成矩陣形式為

其中，Y為數據向量，B為數據矩陣，P為參數向量。

利用最小二乘法求解，可得：

將P=[ab]T代入式(4)，取x(1)(0)=x(0)(1)，解方程得時間相應函數

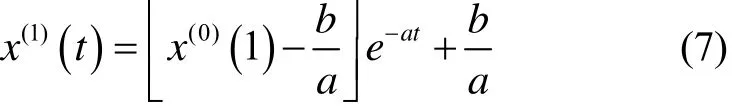
因此，GM(1, 1)灰色微分方程的時間響應序列為

④ 預測k+1時刻的原始數據

灰色模型實際上是生成數列的模型，模型預測的數據需要經過逆生成作還原后才可使用。還原值為

⑤ 模型精度檢驗

檢驗GM(1,1)模型的精度，一般采用殘差檢驗與后驗差檢驗[3]。

1.2 灰色預測模型的改進

灰色系統理論應用表明，原始數據的模式及其光滑特性是影響模型精度的主要因素。為此，本文結合GPS信息特點，對GM(1,1)預測建模過程進行了改進：

① 預處理原始數據，使之滿足序列級比判斷[3]

GPS數據中會出現負數，不能滿足GM(1,1)的建模條件-序列級比判斷。此時，可以將原始數據統一加一個常數，將原始數列轉換為非負數列；或者引入指數映射（如對數-冪函數變換)將原始數據轉換為正數列，并對轉換后的數據進行灰色預測建模可行性的序列級比判斷。最后，將預測結果再進行反變換。

② 增加數據的光滑性，提高GM(1,1)預測精度

GPS導航定位數據還會出現波動現象，使GM(1,1)預測精度降低。為此，本文采用均值預處理的方法，生成一個新序列。然后，對新序列進行GM(1,1)建模。最后通過均值逆算子還原，得到X(0)的預測序列，從而使GM(1,1)模型預測結果的平均相對誤差和后驗差比值明顯減小，提高了預測精度。

③ 實時動態預測

為了及時反映出系統的動態變化，采用了實時動態預測的方法：首先根據原始數據序列X(0)進行一次累加得到X(1)，建立GM(1,1)模型，求得原始數據第k+1時刻的預測值(0)(k+1)。然后對GM(1,1)模型進行改進，在序列中去掉x(0)(1)，加入x(0)(k+1)，構成新序列=｛x(0)(2)，x(0)(3)，···x(0)(n +1)｝進行建模預測。如此遞補，實現動態預測。

2 基于改進型灰色預測模型的GPS故障預測仿真

2.1 正常GPS 數據的預測仿真

以NovAtel OEMV-3-L1型GPS OEM板輸出的位置數據X、Y坐標為例，利用當前時刻前的5個歷史坐標數據，來預測當前時刻的坐標數據。其中，X坐標數據的預測殘差如圖1所示，預測殘差小于1.5 m，滿足了該型GPS定位精度指標要求，即改進型GM(1,1)預測結果能夠很好地跟隨正常GPS數據的動態變化。

圖1 灰色動態預測殘差Fig.1 Dynamic grey forecast residuals

2.2 GPS故障數據預測的仿真

在GPS工作的某一個時間段，實施電子干擾，GPS數據誤差立即增大。X坐標數據及其灰色預測結果如圖2所示。故障點處預測值與GPS實際輸出值之間的殘差明顯增大。

由2.1可知，基于改進型GM(1,1)的預測值是可信、可靠的。因此，在GPS故障期間，由預測數據取代GPS故障數據，一是可以提供與GPS正常時接近的、可靠的數據，二是采用預測數據可以繼續進行動態預測，三是由預測殘差以及故障數據的持續時間和變化特點等可以診斷GPS故障是硬件故障還是外部干擾的影響，有助于實現GPS故障判別與隔離。

圖2 GPS故障數據和灰色預測值Fig.2 GPS failure data and grey forecast values

3 基于改進型灰色預測模型的SINS/GPS仿真

3.1 SINS/GPS組合導航系統非線性數學模型

本文選取SINS為主導航系統，GPS提供量測信息。SINS/GPS組合導航系統非線性數學模型為：

① SINS誤差方程

采用基于加性四元數誤差的SINS 姿態誤差方程和速度誤差方程[6-7]。姿態誤差方程為

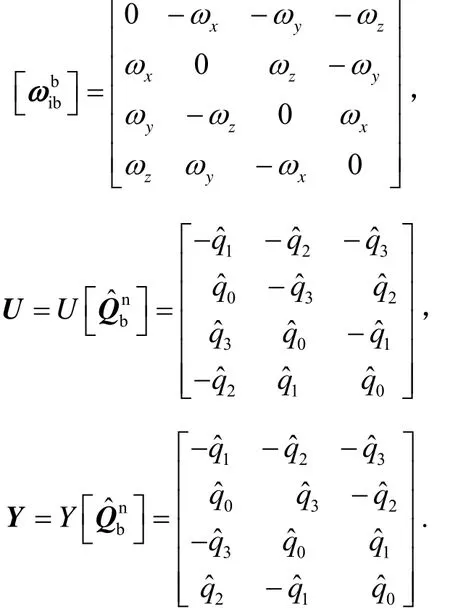
速度誤差方程為

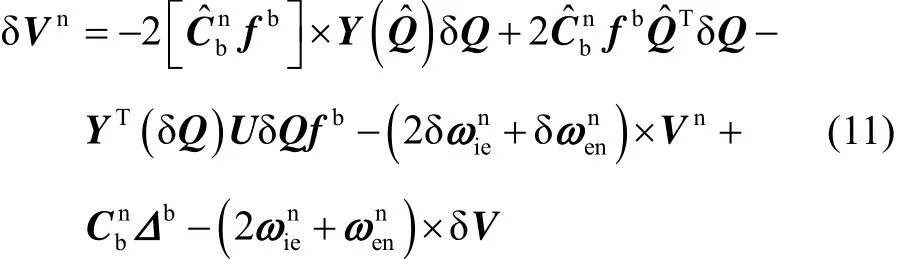
位置誤差方程的矩陣形式為

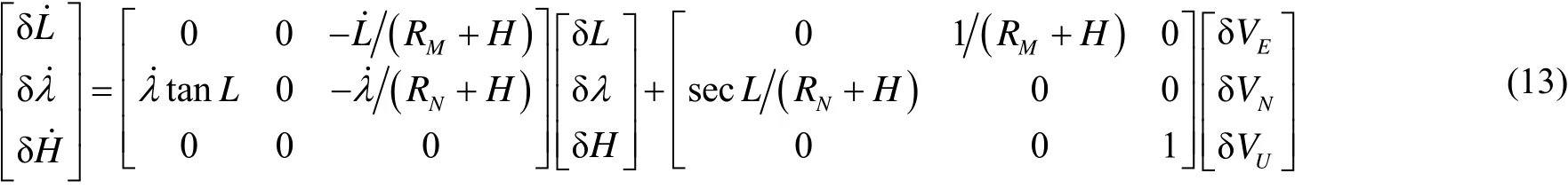
式中：δL、δλ、δH 分別為緯度、經度和高度的誤差；RM和RN分別為沿子午圈和卯酉圈的主曲率半徑。

② SINS/GPS組合導航系統非線性濾波模型

為了估計慣性器件誤差，提高系統模型的精確度，本文將陀螺誤差擴充為狀態變量進行估計。

1）系統狀態方程

根據SINS誤差方程式(10)、(11)和(13)，系統狀態方程可以寫成如下形式：

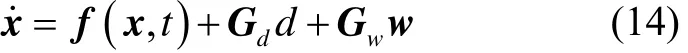
式中：系統的狀態變量

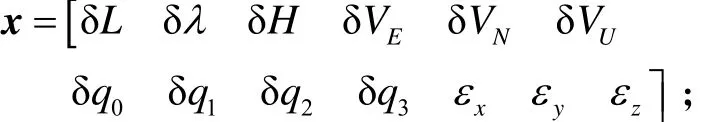
d=[ΔxΔyΔz]T為模型誤差向量；Δx、Δy、Δz、εx、εy、εz分別為加速度計零偏和陀螺漂移，x=y==0；Gd為模型誤差分布矩陣，Gw為過程噪聲輸入矩陣：

2）系統量測方程

取SINS與GPS輸出的位置和速度之差作為量測值，系統量測方程為

式中：y=［δL δλ δH δVEδVNδVU］T為量測變量；v=[vδLvδλvδHvδVEvδVNvδVU]T為量測噪聲，為零均值的高斯白噪聲，其協方差為E(vvT)=R；h=［I6×606×4］為量測矩陣。

3.2 仿真分析

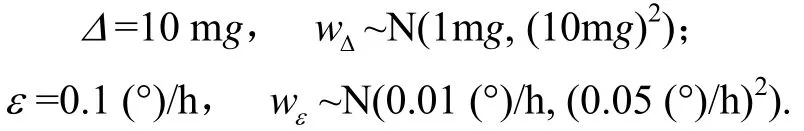
設仿真條件為：其中，wΔ和wε分別為加速度計和陀螺的隨機漂移，且都為高斯白噪聲。GPS的速度量測噪聲為0.1 m/s，位置量測噪聲為10 m。假設載體初始所處的位置緯度L=45°，SINS平臺水平和方位初始誤差角分別為0.05°和0.10°；取狀態估計的初值為0=0， P0=I。

分別采用3.1和3.2的數據，分三種情況進行基于改進型灰色預測的SINS/GPS組合導航系統的仿真：一是GPS正常；二是GPS出現故障，但未對GPS故障進行預測；三是GPS出現故障，但對GPS故障進行了改進型灰色動態預測。其中，SINS/GPS組合導航系統輸出的X坐標仿真曲線如圖3所示。由圖3可得：

① 當出現GPS故障時，GPS為SINS/GPS組合導航系統提供誤差較大的量測信息。當沒有對GPS故障進行故障預測時，SINS/GPS組合導航系統輸出的位置誤差越來越大。該誤差將使航天器偏離軌道。

② 出現GPS故障時，如果對GPS故障數據采用基于灰色動態預測的故障預測，可以得到接近于GPS正常時的預測數據。以預測數據取代GPS故障數據，可以為SINS/GPS組合導航系統提供誤差較小的量測信息，有效提高了SINS/GPS的抗干擾能力，保證了SINS/GPS組合導航系統的導航定位精度。

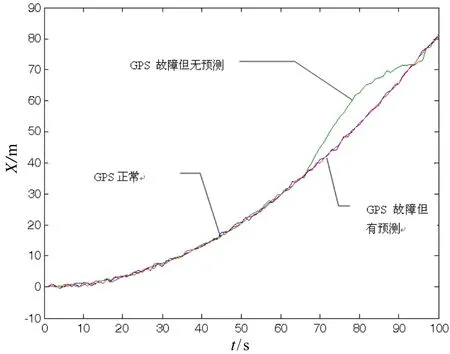
圖3 SINS/GPS組合導航系統輸出的X坐標曲線Fig.3 Curves of outputted coordinate X from SINS/GPS

（References）：

[1] Biros O, Karchnak J, Simsik D, Hosovsky A. implementation of wearable sensors for fall detection into smart household[C]//IEEE 12th International Symposium on Applied Machine Intelligence and Informatics. 2014: 19-22.

[2] Salman H K, Muhammad S. Activity monitoring of workers using single wearable inertial sensor[C]//International Conference on Open Source Systems and Technologies. 2013: 60-67.

[3] Bathurst S P, Kim S G. Designing direct printing process for improved piezoelectric micro-devices[J]. CIRP Annalsmanufacturing Technology, 2009, 58(1): 193-196.

[4] Hou Ming-chang. Design and fabrication of MEMS-array pressure sensor navigation inspired by lateral line[D]. Massachusetts Institute of Technology, 2012: 95-110.

[5] 朱玉芳, 楊繼全, 岳東. 多材料模型的數字化噴射成型方法[J]. 機械科學與技術, 2009, 28(2): 200-204. Zhu Yu-fang, Yang Ji-quan, Yue Dong. Digital injecting process of multi-material objects[J]. Mechanical Science and Technology for Aerospace Engineering, 2009, 28(2), 200-204.

4 結 論

本文根據灰色預測理論和SINS/GPS中GPS導航定位信息的特點，提出了基于改進型灰色預測的GPS故障預測模型，并結合SINS/GPS組合導航系統的非線性模型，進行了仿真。仿真結果證明，將GPS故障預測模型嵌入SINS/GPS組合導航系統，可以為SINS/GPS提供與GPS正常時接近的可靠可信的導航定位信息；由預測數據取代GPS故障數據可以有效提高SINS/GPS組合導航系統抗干擾能力，保證SINS/ GPS組合導航系統的導航精度；比較GPS故障數據和預測數據，并根據故障數據的持續時間和變化情況等，可以診斷GPS故障是硬件故障還是外部干擾的影響，有助于實現GPS故障判別與隔離。因此，基于改進型灰色預測模型的SINS/GPS組合導航系統在航天器等領域具有一定的應用價值與前景。

參考文獻（References）：

[1] 姜連祥, 李華旺, 楊根慶. 航天器自主故障診斷技術研究進展[J]. 宇航學報, 2009, 30(4): 1320-1324. Jiang Lian-xiang, Li Hua-wang, Yang Gen-qing. A survey of spacecraft autonomous fault diagnosis research[J]. Jounal of Astronautics, 2009, 30(4): 1320-1324.

[2] 周志杰, 胡昌華, 周東華. 基于非解析模型的動態系統故障預報技術[J]. 信息與控制, 2006, 35(5): 608-612. Zhou Zhi-jie, Hu Chang-hua, Zhou Dong-hua. Fault prediction techniques for dynamic systems based on nonanalytical model[J]. Information and Control, 2006, 35(5): 608-612.

[3] 李小力, 李言俊, 張科. 改進的灰色預測模型在導彈中的應用[J]. 計算機仿真, 2010, 27(8): 33-39. Li Xiao-li, Li Yan-jun, Zhang Ke. Improved grey forecasting model of fault prediction in missile applications[J]. Computer Simulation, 2010, 27(8): 33-39.

[4] Keller J Y, Saute D. Restricted diagonal detection filter and updating strategy for multiple fault detection and isolation[J]. International Journal Of Adaptive Control and Signal Processing, 2010, 1210(1): 68-87.

[5] 翁浚, 成研, 秦永元, 嚴恭敏. 車輛運動約束在SINS/OD系統故障檢測中的應用[J]. 中國慣性技術學報, 2013, 21(3): 406-409. Weng Jun, Cheng Yan, Qin Yong-yuan, Yan Gong-min. Application of vehicle constraints in SINS/OD system’s fault detection[J]. Journal of Chinese Inertial Technology, 2013, 21(3): 406-409.

[6] Yu M J, Park H W, Jeon C B. Equivalent nonlinear error models of strapdown inertial navigation systems[R]. AIAA-97-3563, 1997.

[7] Bortz J E. A new mathematical formulation for strapdown inertial navigation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1971, AES-7(1): 61-66, 287-291.

[8] Wang Y, Chan C W, Cheung K C. On-line fault diagnosis based on b-spline neural networks using asymptotic local approach[J]. Asian Journal of Control, 2008, 321(1): 73-78.

[9] Zhang Ying-wei, Qin S J. Improved nonlinear fault detection technique and statistical analysis[J]. Aiche Journal, 2008, 17(12): 3207-3220.

SINS/GPS integrated navigation system based on improved grey forecasting model

WANG Li-dong1, CHE Lin2, LU Jun1, GAO Qing1
(1. Ordnance Engineering College, Shijiazhuang 050003, China; 2. Huayin Ordnance Test Center of China, Huayin 714200, China)

To forecast the GPS failure in SINS/GPS integrated navigation system, a forecast model based on improved grey prediction is presented based on the characteristics of GPS navigating and positioning information. Combining with the mathematical model of SINS/GPS integrated navigation system, the simulation based on the improved grey prediction model is carried out, and the results show that the predicted residual of GPS position data is less than 1.5 m, and during the transient failure of GPS, the anti-interference ability of SINS/GPS integrated navigation system can be improved by replacing the GPS failure data with the forecasted data. Based on the comparison of GPS failure data and prediction data, and according to the duration and changing characteristics of failure data, it is able to diagnose the GPS failure is whether a hardware failure or due to external factors, which helps to carry out the recognition and isolation of GPS failure.

control and navigation; grey forecast model; failure forecast; integrated navigation

U666.1

A

1005-6734(2015)02-0248-04

10.13695/j.cnki.12-1222/o3.2015.02.019

2014-11-20；

2015-03-25

國家自然科學基金項目（60671045）

王立冬（1965—），男，副教授，研究方向為光纖慣導技術。E-mail：wlddoctor@163.com