結合天線互耦分析的同車電臺射頻干擾對消

劉建成，趙宏志，全厚德，崔佩璋，唐友喜，孫慧賢

（1.軍械工程學院信息工程系，河北石家莊050003；2.電子科技大學通信抗干擾技術國家級重點實驗室，四川成都611731）

結合天線互耦分析的同車電臺射頻干擾對消

劉建成1，趙宏志2，全厚德1，崔佩璋1，唐友喜2，孫慧賢1

（1.軍械工程學院信息工程系，河北石家莊050003；2.電子科技大學通信抗干擾技術國家級重點實驗室，四川成都611731）

伴隨戰場指揮通信系統的復雜化，車載多部軍用超短波（very high frequency，VHF）電臺間互擾問題日益突出。針對同車電臺間互擾問題，提出了結合天線近場耦合計算的射頻干擾自適應對消方法，在此基礎上推導出了耦合計算誤差影響系統收斂時間的解析表達式。該方法通過預先建立同車收發天線近場模型，計算得出收發天線間耦合系數和相位失真度，再利用該結果設定自適應干擾對消鏈路的初始參數，縮短了射頻自適應干擾對消算法的收斂時間。仿真表明，所提方法在不降低對消比情況下，與現有的自適應對消方法相比收斂時間縮短了30%以上，同時也驗證了計算誤差影響收斂時間解析表達式的正確性。

電臺互擾；近場耦合；自適應干擾對消；收斂時間

0 引 言

隨著戰場信息化的發展，各級指揮通信系統日趨復雜，大量電子設備裝備于同一指揮系統，設備間存在嚴重的相互干擾，使得戰場電磁環境日益復雜。比如，同一輛通信指揮車上通常裝備有多部短波和超短波（very high frequency，VHF）電臺，多部電臺間存在嚴重的鄰道干擾，即使在頻分情況下也不能夠同時正常工作。其原因在于，相鄰電臺輻射的電磁波在接收機天線處產生很強的干擾電壓，超出了接收機的動態范圍，造成接收機阻塞。

針對電臺間的互擾問題，國內外都進行了深入的研究，相關成果也在實際設備中得到了應用。20世紀70年代末美國的Harris S J和Rosasco S J提出了利用相位微調器與正交矢量合成相結合的閉環干擾和噪聲對消系統，在干擾信號功率為幾十瓦量級時，能夠實現40 dB以上的對消比［1］，但該系統對移相器和電調衰減器的性能要求高，由于未采用自適應的調節方法，系統收斂時間長（大于20 ms），無法滿足現役VHF電臺的需求。文獻［2］中進一步提出了一種寬頻帶對消系統，工作波段為225～400 MHz。該系統采用發射導頻的雙環自適應對消工作模式，可在fc±85 k Hz范圍得到大于50 d B的干擾對消比，不過該自適應對消過程的系統收斂性有待進一步提高。文獻［3］中分析了正交兩路信號控制精度對自適應干擾對消系統性能的影響；文獻［4- 6］中都分析了對消系統中兩條支路的延時誤差對性能的影響；文獻［7］將功放的線性化技術應用在了對消鄰道干擾中，但均未明確給出改善系統收斂速度的方法；文獻［8］提出利用光通信實現本地收發間的干擾對消，但該方案的應用受到限制；文獻［9］研究分析了最小均方（least mean square，LMS）自適應算法的低復雜度實現問題；文獻［10- 12］將自適應對消系統應用于同時同頻全雙工（co-frequency co-time full duplex，CCFD）通信中，取得了55 dB以上的對消比，不過文獻中并未分析收發天線間耦合關系；文獻［13］中只是分析了同車收發設備間共址干擾產生機理及其對設備性能的影響。上述文獻中的干擾對消方法收斂時間長，當應用于軍用電臺的跳頻通信方式時，不能夠有效滿足快跳速對系統對消處理時間的要求。

為此，本文從預設初始參數縮短系統收斂時間的角度出發，提出了通過預分析計算同載體平臺收發天線間近距離耦合參數，再以查詢表的方式輔助射頻干擾自適應對消的方法。仿真表明，該方法能夠有效縮短系統收斂時間，為對消系統在高速跳頻電臺中應用奠定了基礎，同時也適用于目前廣泛研究的CCFD。另外，為避免理論分析計算的天線耦合參數與實際值誤差較大，可通過實際訓練測量加以修正。

1 已有射頻干擾對消模型

圖1是已有文獻中提出的自適應干擾對消系統［25］，該對消系統主要由移相器、衰減器和誤差控制器組成。該系統首先在發射天線耦合器前導出參考信號，再通過90°相移器分為正交的i和q兩路信號，每一路分別由相應的衰減器控制其幅度，之后再進行合并生成重建信號Sc（t），最后與接收機天線接收的干擾信號SI（t）進行反相合并對消，輸出期望信號r（t）。該系統的自適應性體現在通過誤差反饋信息控制衰減器，進而改變重建新號的幅度和相位，改善最終的干擾對消比（interference cancellation ratio，ICR），即對消前后的干擾信號功率之比。

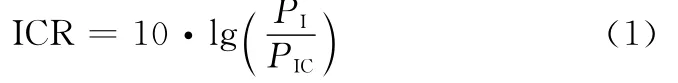
式中，PI為對消前的干擾信號功率；PIC為對消后的殘余干擾信號功率。

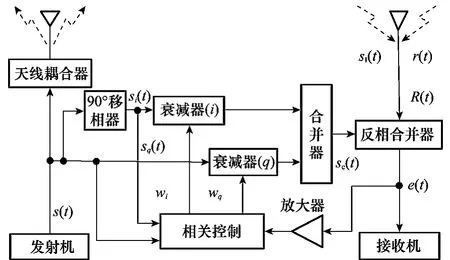
圖1 已有干擾對消系統模型

由于無輔助信息，系統中i、q兩路衰減器的初始參數一般為1，合成的初始重建信號與干擾信號相差較大。在誤差放大器和控制參數一定（自適應的步長因子為定值）時，整個自適應誤差反饋控制鏈路的收斂時間較長，影響了整個對消系統的效能發揮。為此，本文后續部分提出了基于天線互耦分析的干擾對消模型，通過設定兩路衰減器初值，有效降低了系統收斂時間。

2 天線近場互耦的數學分析

現有的陸基VHF戰術指揮通信系統以車載方式為主，使用天線多是全向鞭狀天線。為便于分析，同時不失其一般性，本文以車頂上安置的兩副相同鞭狀天線為例，進行互耦分析，具體結構如圖2所示，多副天線情形可以此類推。車體上兩副天線間的距離較近，一般在VHF波段的λ／10～λ／4，屬于天線輻射的近場區和菲涅耳區，不能以遠場區的公式進行計算分析，所以這里采用電磁分析中常用的矩量法計算分析兩副天線間的耦合關系［1415］，為獲取本文對消方法中的耦合參數提供理論分析。

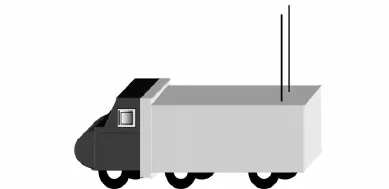
圖2 指揮通信車模型

由于天線相距較近，車體是具有良好導電性的鐵質材料，問題分析可等效于有限導體平面上兩副半波直立細天線的耦合關系分析。在分析過程中需要將兩副天線與車體視為一個整體，統一進行剖分，充分考慮它們之間的互耦效應，如圖3所示。

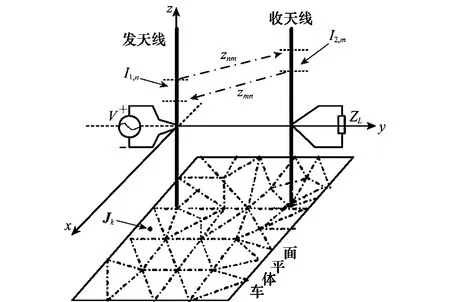
圖3 天線耦合分析圖

電磁場分布及耦合關系的計算分析，關鍵是求解每一個剖分單元的分布電流I1，n、I2，m、Jk及它們之間的互阻抗znm、zmn，已知分布電流后即可由電場強度E與矢量位H之間的關系，計算得出發射天線上分布電流在接收天線表面上產生的感應電場強度E21，進而求得接收天線負載上的電壓I2（0）ZL，即接收天線輸出的信號sI（t）強度及其相位信息。這里I2（0）和ZL分別表示收天線饋源處的電流值及其阻抗（假設發射天線阻抗同為ZL）。

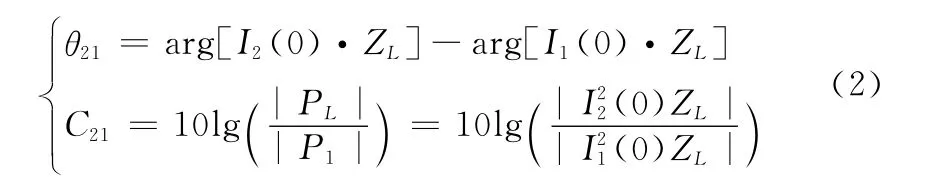
式中，arg（）表示求復數的輻角。

若假設發天線發送信號的幅度為A，收天線接收信號幅度為A′，則A與A′之間滿足如下關系：

由式（2）和式（3）所示的相位延遲和耦合關系計算結果即可構建對消鏈路，實現對本地射頻干擾信號的有效對消。

3 基于天線互耦分析的自適應干擾對消

在通過理論分析和實際訓練測量獲得較為準確的天線間互耦參數基礎上，本節給出基于查詢表方式的自適應對消鏈路初值設定模型，如圖4所示，實現具有較短收斂時間的干擾對消。該干擾對消方法利用了天線間近場互耦關系，得出干擾信號sI（t）相對于參考信號s（t）在幅度和相位上的失真，進而通過控制兩路衰減器縮短對消環路的收斂時間。

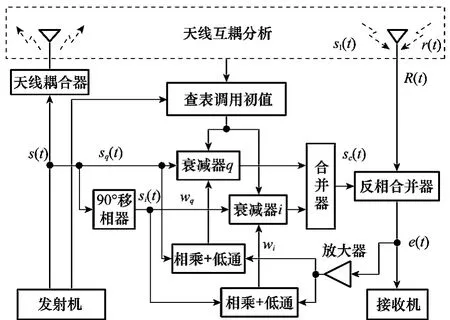
圖4 本文干擾對消模型

由于指揮車一般會選擇平坦開闊地域，且收發天線處于彼此的近場區或菲涅耳區，所以接收天線的干擾信號主要是通過直接耦合方式產生，其他反射路徑產生的干擾信號相對而言一般屬于弱小信號，不會阻塞接收機，可在后續的數字域進行抑制處理，這里不再考慮。

假設在發射機天線耦合器前端的信號為

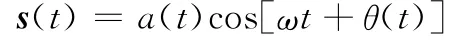
經天線互耦通道進入接收機前端（射頻調諧濾波前）后，信號變為

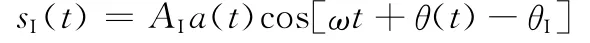
其中相位θI中已包含路徑傳輸延遲的影響，接收機天線接收到的期望信號為r（t）。

由以上假設可知，接收機天線輸出信號的表達式為

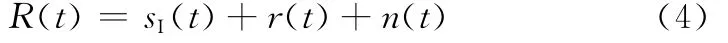
式中，n（t）為高斯白噪聲。

如圖4所示，假設由前述內容計算分析得出本地干擾信號為

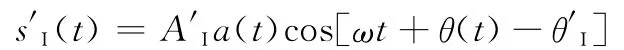
則可根據相位結果θ′I和幅度結果A′I分別控制衰減器，最終合成需要的干擾重建信號。對消系統中由傳輸線而導致的相位延遲和功率損耗可認為是定值，只需在衰減器參數設置中加以考慮，減去對應值即可，所以不再考慮該部分對相位和幅度的影響。

已知i路信號和q路信號與原信號間相位差分別為φi＝90°和φq＝0°，再根據互耦分析結果θ′I和A′I可計算出兩路衰減器的初始值Ai和Aq，則在無反饋調節下圖1中兩路信號si（t）和sq（t）經衰減器后可分別表示為

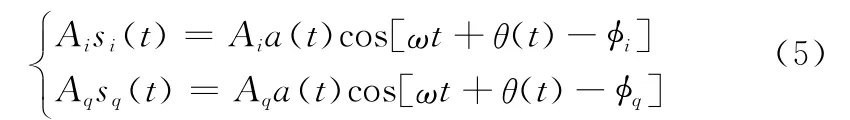
令Δφi＝θ′I－φi，Δφq＝θ′I－φq。合并后的干擾重建信號為

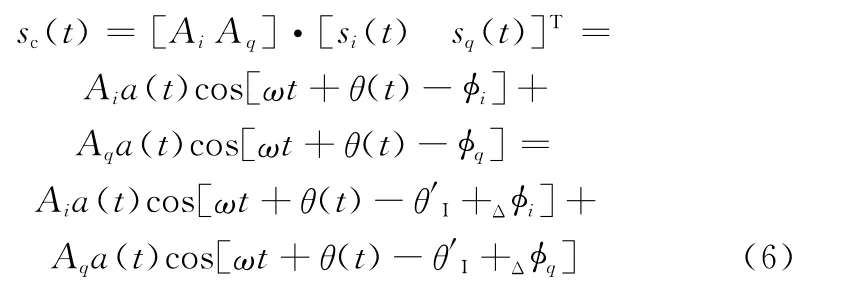
化簡整理得

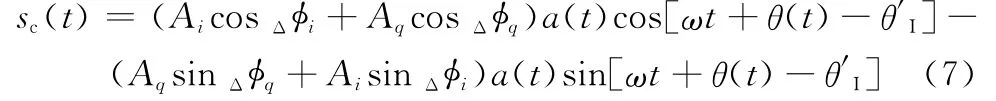
可見，若以計算的本地干擾信號s′I（t）為對消目標信號，欲取得最佳干擾對消效果，則輸入反相合并器的重建信號sc（t）中相關控制參量需滿足以下關系：

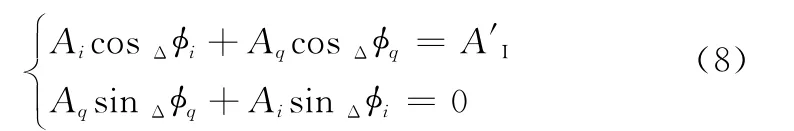
即

由前述推導可知，式（9）中Δφi、Δφq和A′I已知，通過求解該式即可得兩路衰減器的初始值Ai和Aq

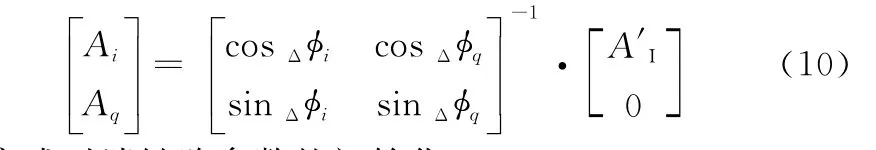
至此，完成對消鏈路參數的初始化。

由于天線互耦計算結果中的干擾信號s′I（t）與實際干擾信號sI（t）之間可能存在誤差，可通過對消后信號進行反饋調節衰減器，進一步降低誤差，得到更高的ICR。

由以上分析可知，經反饋誤差調節后的重建信號可表示為

式中，wi（t）和wq（t）為兩路衰減器權值；τ為一次反饋迭代所需的假設時間（其值與衰減器和低通濾波器時間常數有關，具體分析可見文獻［4，6］）。由式（11）將對消后殘余信號表示為

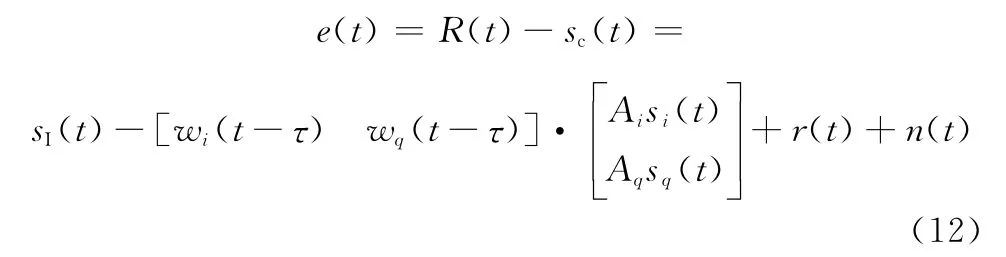
可見，欲使ICR達到最大，則對消后殘余信號需要滿足以下準則：

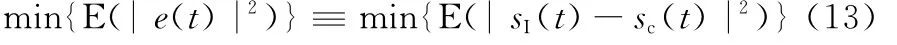
根據最小均方誤差準則可建立LMS算法的干擾對消過程，設步長因子為μ，i和q兩路的權值在t－τ與t時刻之間的迭代計算過程如下：

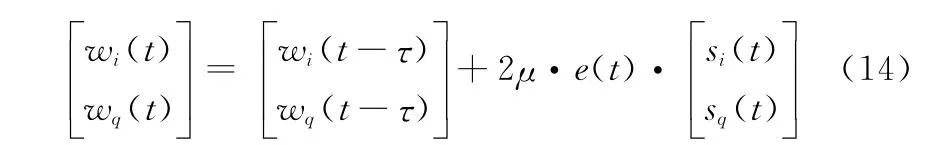
由以上的描述過程可有效對消相鄰發射設備的射頻干擾。

4 干擾對消方法性能分析

在建立了結合天線耦合分析的自適應干擾對消模型基礎上，本節首先分析了自適應干擾對消方法中初始誤差對系統收斂時間的影響，進而分別推導出了已有的自適應對消方法和本文方法所對應的收斂時間解析表達式，得出了本文方法中天線互耦計算誤差與收斂時間的關系。

4.1 自適應干擾對消系統收斂時間分析

下面推導系統收斂時間與初始誤差的關系，為方便推導式（13）與式（14）之間的關系，現將信號以向量形式表示如下：

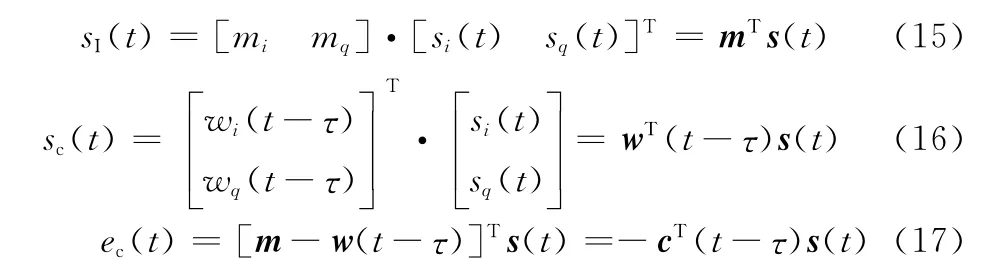
式中

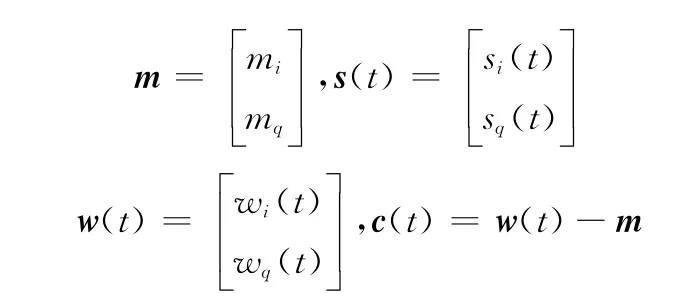
由信號s（t）特性可設E｛sT（t）s（t）｝＝K，K為常量。所以有E｛s（t）sT（t）｝＝·I，I為單位矩陣，則式（13）中的誤差均方值可等價為

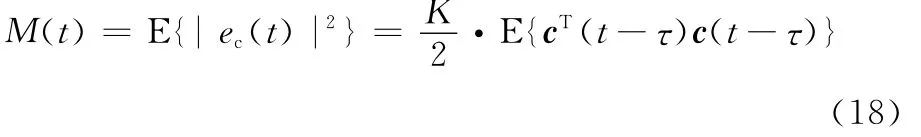
由式（14）可知

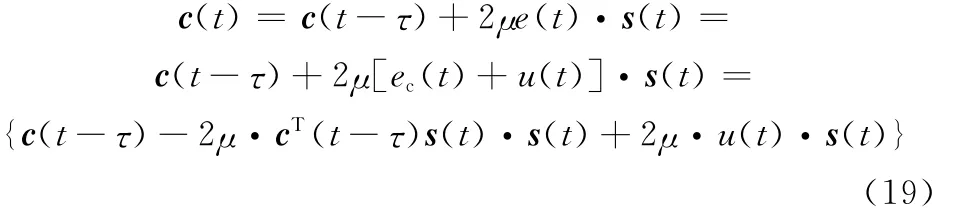
代入式（18），得

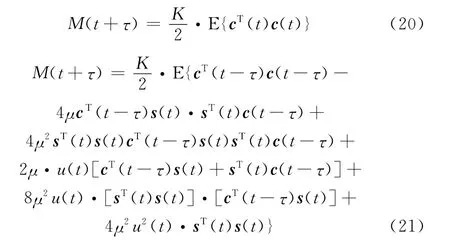
又因為

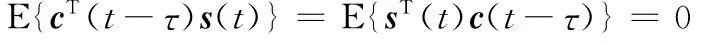
所以有

即

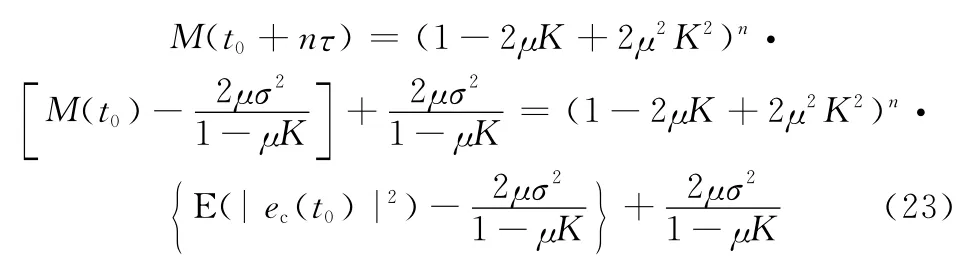
式中，σ2＝E（｜u（t）｜2）為期望信號和噪聲的均方值，為常量。參考文獻［18］，可見系統收斂需要滿足

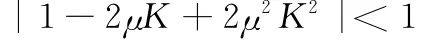
即

由式（15）和天線接收信號表達式可知，對消前的干擾信號均方值為

所以這里假定μ取值在收斂范圍內，在t0＋nτ時刻系統的ICR可表示為

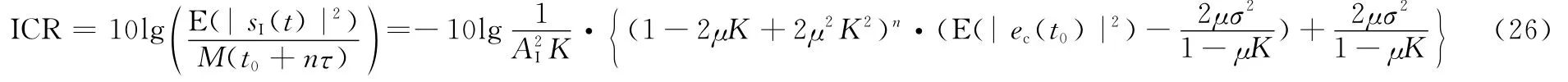
由式（26）可得，ICR一定時對應的系統收斂時間為

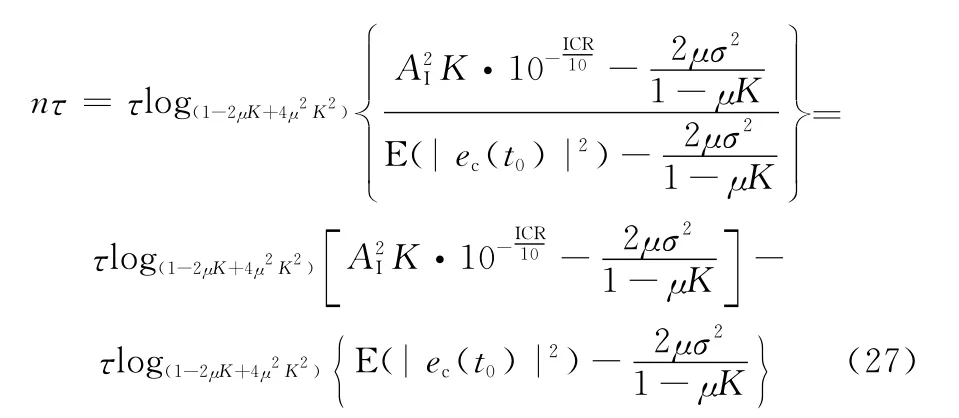
由于AI、K、ICR、σ2和μ均為常量，所以該式可簡化為

式中

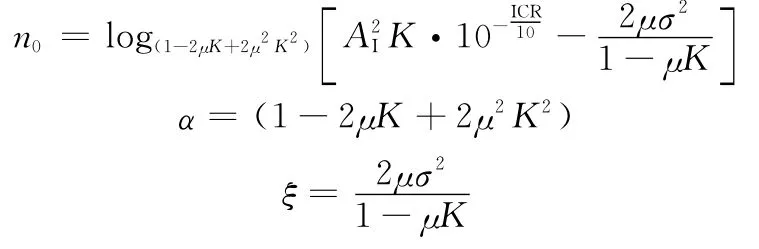
可見，步長因子μ和系統ICR一定情況下，式（28）即為系統收斂時間與初始誤差ec（t0）間的約束關系，由該式即可分別求得已有方法和本文方法對應的收斂時間。

4.2 已有方法收斂時間

首先，給出已有方法中的初始對消誤差表達式（這里只分析互耦計算誤差對系統收斂時間的影響，所以不再考慮文獻［5］中所分析的兩路正交信號時延不匹配問題）。設已有方法中兩路衰減器初始權值均為1，即初始的重建信號為

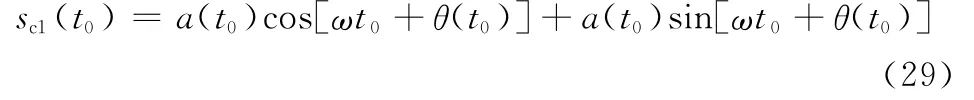
令u（t）＝r（t）＋n（t），定義滿足式（13）的對消誤差為ec（t）＝e（t）－u（t），則現有方法中初始時刻t0的對消誤差為

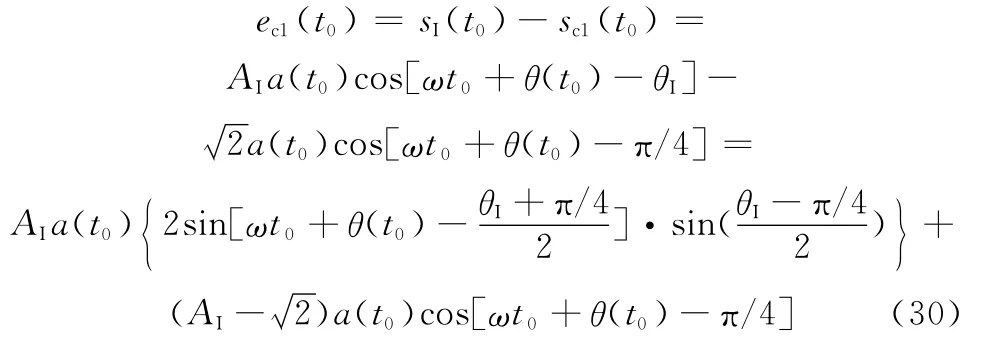
代入式（28）可得收斂時間

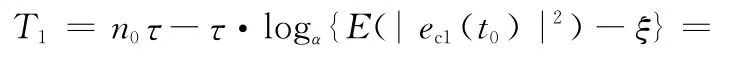
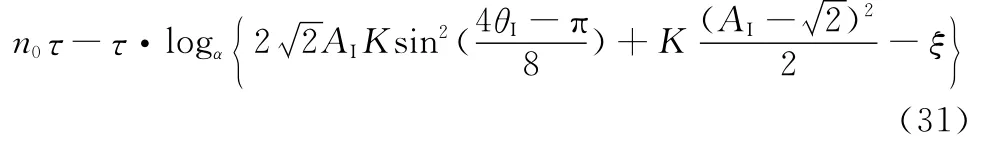
4.3 本文方法收斂時間

參考第4.2節，由式（9）和式（10）的參數初始化過程可知，本文所提方法中合成的初始重建信號為

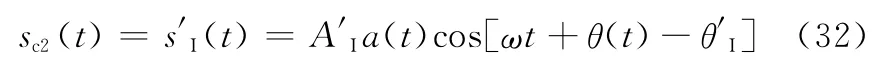
同理可得本文方法中的初始對消誤差為

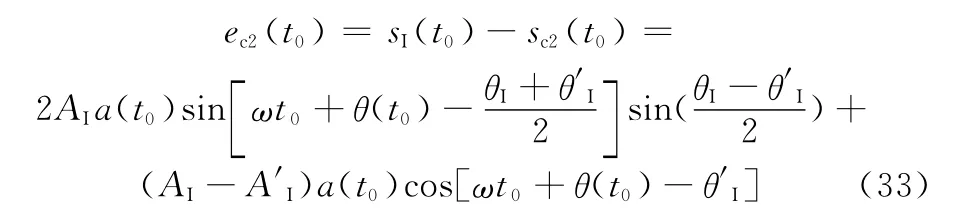
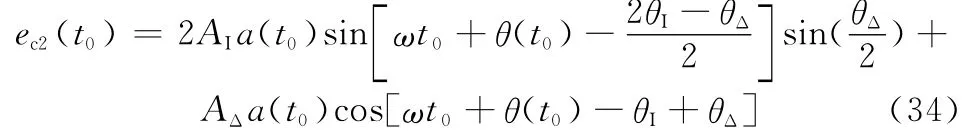
代入式（28）可得本文方法收斂時間的解析表達式

可見，該解析表達式同時反映了天線互耦計算誤差對系統收斂時間的影響。

5 仿真實驗

仿真以實際情況為參考，設車和天線的尺寸參數分別為：平臺車體長約6.5 m，寬2.5 m，高2.2 m；鞭狀天線長3.2 m（中部饋電，半徑為0.01 m），間距為1.5 m；兩部電臺采用正交相移鍵控（quadrature phase shift keying，QPSK）調制方式，傳輸速率為9.6 kbps；發射電臺天線饋源處信號功率為37 dBm；接收電臺天線耦合的期望信號功率為－67 dBm；收發電臺信道間隔200 k Hz，分別工作于54.0 MHz和54.2 MHz；天線輸出端口噪聲限為－110 dBm（假設發射機耦合器已調諧）。

由上述互耦分析方法可計算出VHF電臺常用工作頻率在30～88 MHz范圍內，天線1與天線2之間的耦合系數、天線2上負載處電流的相位，二者與發射信號頻率之間的關系分別如圖5和圖6所示（實際應用中，可通過不同環境下的多次實際測量數據對結果進行修正，從而減小誤差）。

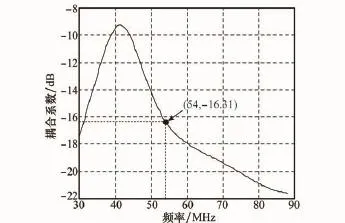
圖5 30～88 MHz天線耦合系數與頻率間關系

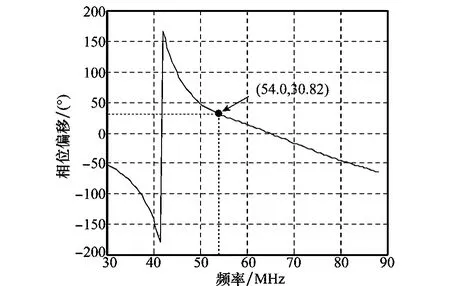
圖6 30～88 MHz天線耦合相位失真與頻率間關系

由圖5可知，在發射頻率為41.5 MHz時耦合系數達到最大值，圖6中ZL上電流相位取值［－180°180°］，在41.5 MHz時為－180°，這體現了天線間的電抗性，具體分析可見文獻［14］。對于本文仿真所采用的54.0 MHz發射頻率，耦合系數為－16.31，相位為30.82°（即－329.18°）。

由上述仿真計算得天線2負載上的本地干擾信號相位θ′I＝30.82°，根據發射功率P＝5 W、耦合系數C21＝－16.31 d B、負載ZL＝50Ω和式（3）即可求得天線2負載上的本地干擾信號幅度。

現分析接收天線輸出的信號，由以上內容可得該信號功率譜密度如圖7所示，可見期望信號強度要遠小于本地發射機所產生的干擾信號，兩者相差80 dB以上，對于54.2 MHz頻率處的干擾信號的帶外譜也要比期望信號強20 dB以上，所以較強的本地射頻干擾會阻塞接收機，必須在射頻帶通濾波前進行干擾對消。

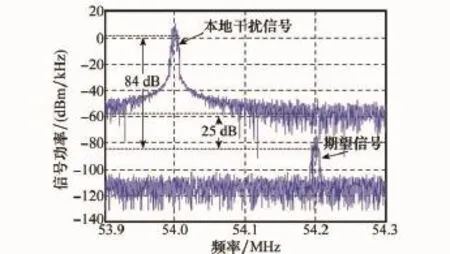
圖7 接收天線輸出信號頻譜

［6］中對步長因子μ大小與對消后期望信號損耗間關系的分析，這里取μ＝（1／K）×10－4，由上文分析可知K約等于2倍發射天線耦合器輸入信號的平均功率P（單位：mW）。假設天線耦合計算的干擾幅度和相位延遲誤差分別為θΔ＝2.5°，AΔ＝0.2A′I。圖8對應的是已有方法和本文方法在不同時間達到的ICR。可見，已有的自適應對消方法在t＝1.3×10－4s之后開始趨于收斂狀態，而本文方法是在t＝0.8×10－4s（小于一個基帶碼元持續時間）。分析經t＝0.8×10－4s時對消誤差信號的頻譜，如圖9和圖10所示，可見本文方法在該時刻已獲得60 dB以上的ICR，遠高于現有方法，結合圖8表明本文方法收斂時間明顯短于現有方法。

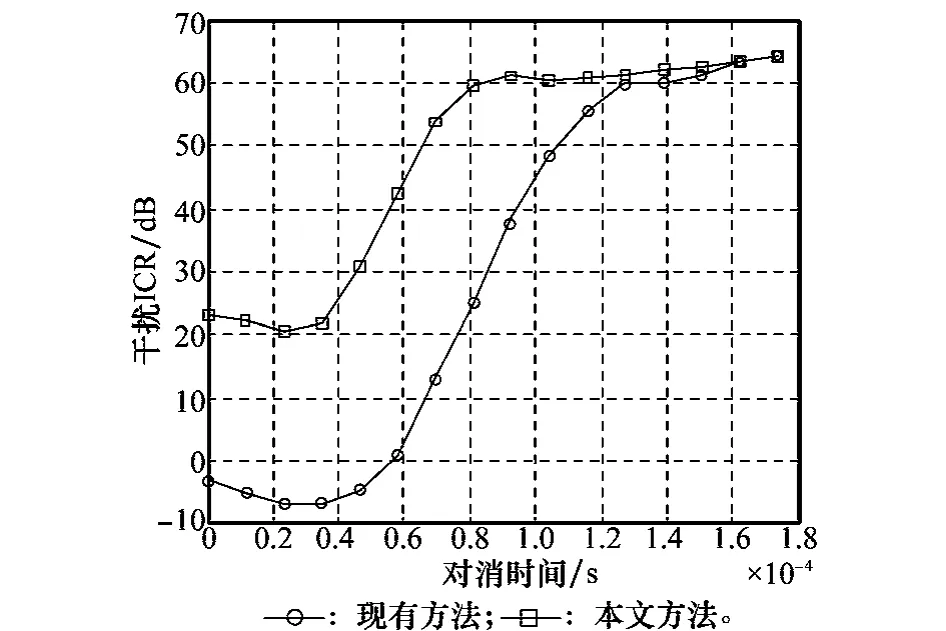
圖8 不同時間達到的ICR

圖9 t＝0.8×10－4s時現有方法對消誤差頻譜

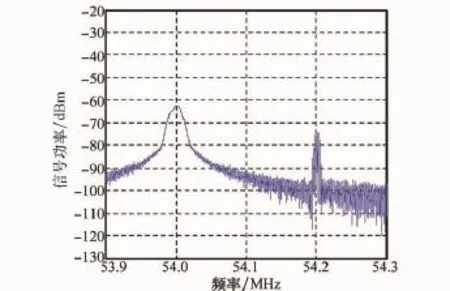
圖10 t＝0.8×10－4s時本文方法對消誤差頻譜

下面以ICR＝60 dB為系統收斂門限，步長因子μ同上，仿真分析本文方法中天線互耦計算誤差θΔ和AΔ對系統收斂時間的影響。圖11是根據仿真條件和式（35）計算出的所需收斂時間與相位、耦合幅度計算誤差之間的理論曲面。圖12是系統收斂時間在幅度計算誤差AΔ分別為0.05A′I、0.1A′I、0.3A′I、0.5A′I時，與相位計算誤差間的關系，圖13反映的是系統收斂時間在相位計算誤差θΔ分別為0.5°、2°、5°、10°時，隨幅度計算誤差的變化。

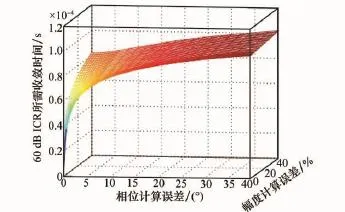
圖11 互耦計算誤差與系統收斂時間關系

圖12 相位分析誤差對應的系統收斂時間

圖13 耦合系數分析誤差對應的系統收斂時間

分析圖12和圖13，可見圖12中4條曲線變化較大，即在相位計算誤差一定情況下幅度計算誤差對系統收斂時間影響較大；圖13反映出在幅度計算誤差大于20%時，相位計算誤差對系統收斂時間影響較小；結合圖12和圖13可見在相位和幅度計算誤差分別為20°和30%時，系統收斂時間約為0.9×10－4s，比現有方法的1.35×10－4s（見圖8）減小了30%以上，能夠適用于天線耦合參數具有一定誤差的情況。另外，比較圖12、圖13和圖11，可見計算誤差分析曲線與式（35）所得曲面相符合，從而驗證了文中所推導的計算誤差影響收斂時間解析表達式的正確性。

6 結 論

本文結合近距離天線間互耦分析，通過理論計算和實際數據測量得出發射天線在接收天線產生干擾的幅度衰減和相位失真，進而設定對消系統的初始參數，減小初始誤差，在不降低ICR的前提下，有效縮短了系統收斂時間。仿真表明，該方法在天線耦合參數具有一定誤差情況下，系統收斂時間仍能夠小于10－4s，與已有的自適應對消方法相比縮短了30%以上。另外，本文還分析推導了互耦計算誤差影響系統收斂時間的解析表達式，并通過仿真驗證了其正確性。本文建議的自適應干擾對消方法只需預先得出天線間的耦合關系，實現了同等ICR下的快速收斂。所以，該方法為解決同載體快速跳頻電臺間互擾問題奠定了基礎，同時在其他無線收發設備互擾抑制中也具有重要的應用意義。

參考文獻：

［1］Harris S J，Rosasco S J.High power HF and noise cancellation system［R］.RADC-TR-80- 56.New York：Rome Air Development Center，1980.

［2］Lee D W，Burton S A.High power broadband cancellation system［R］.RADC-TR-81-15.New York：Rome Air Development Center，1981.

［3］Ma Y G，Du W L.Performance analysis and design of adptive interference cancellation system［J］.Journal of Xidian University，1992，19（1）：84- 92.（馬義廣，杜武林.自適應干擾抵消系統的性能分析與設計［J］.西安電子科技大學學報，1992，19（1）：84- 92.）

［4］Li W L，Zhao Z H，Tang J，et al.Performance analysis and optimal design of the adaptive interference cancellation system［J］.IEEE Trans.on Electromagnetic Compatibility，2013，55（6）：1068- 1075.

［5］Syrjala V，Valkama M，Anttila L，et al.Analysis of oscillator phase-noise effects on self-interference cancellation in full-duplex OFDM radio transceivers［J］.IEEE Trans.on Wireless Communications，2014，13（6）：2977- 2990.

［6］Choi Y S，Hooman S M.Simultaneous transmission and reception：algorithm，design and system level performance［J］.IEEE Trans.on Wireless Communications，2013，12（12）：5992- 6010.

［7］Varahram P，Mohd A B，Mohammady S，et al.Power amplifier linearisation scheme to mitigate superfluous radiations and suppress adjacent channel interference［J］.IET Communications，2014，8（2）：258- 265.

［8］Chang J，Prucnal P R.A novel analog photonic method for broadband multipath interference cancellation［J］.IEEE Microwave and Wireless Components Letters，2013，23（7）：377- 379.

［9］Meher P K，Park S Y.Critical-path analysis and low-complexity implementation of the LMSadaptive algorithm［J］.IEEE Trans. on Circuits and Systems I：Regular Papers，2013，61（3）：778- 788.

［10］Anttila L，Korp I D，Syrj?l?V.Cancellation of power amplifier induced nonlinear self-interference in full-duplex transceivers［C］∥Proc.of the Asilomar Conference on Signals，Systems and Computers，2013：1193- 1198.

［11］Bharadia D，Mc Milin E，Katti S.Full duplex radios［C］∥Proc.of the ACM SIGCOMM Computer Communication Review，2013：375- 386.

［12］Xu Q，Quan X，Pan W S，et al.Analysis and experimental verification of RF self-interference cancelation for co-time cofrequency full-duplex LTE［J］.Journal of Electronics&Information Technology，2014，36（3）：662- 668.（徐強，全欣，潘文生，等.同時同頻全雙工LTE射頻自干擾抑制能力分析及實驗驗證［J］.電子與信息學報，2014，36（3）：662- 668.）

［13］Zhao B，Quan H D，Cui P Z.Quantitative ananlysis on radio co-site interference［J］.Journal of Radio Science，2011，26（5）：837- 843.（趙波，全厚德，崔佩璋.無線電同址干擾定量分析方法研究［J］.電波科學學報，2011，26（5）：837- 843.）

［14］Orfanidis S J.Electromagnetic waves and antennas［M］.New Brunswick：Rutgers University，2014.

［15］Ursula C R，Maicon V M，Marcio M A.Evaluation of singular integral equation in Mo M analysis of arbitrary thin wire structures［J］.IEEE Trans.on Magnetics，2014，50（2）：457- 460.

［16］Mohan A，Daniel S W.Accurate modeling of the cylindrical wire kernel［J］.Microwave and Optical Technology Letters，2006，48（4）：740- 744.

［17］Wang Z G，Sun Y F，Wang G H.Analysis of electromagnetic scattering characteristics from conducting targets using improved fast dipole method and characteristic basis function method［J］.Journal of Electronics&Information Technology，2013，35（9）：2272- 2277.（王仲根，孫玉發，王國華.應用改進的快速偶極子法和特征基函數法分析導體目標電磁散射特性［J］.電子與信息學報，2013，35（9）：2272- 2277.）

［18］Dimitris G M，Vinay K I，Stephen M K.Statistical and adaptive signal processing［M］.New York：McGraw-Hill Companies，2000.

劉建成（198-7- ），男，博士研究生，主要研究方向為無線通信干擾抑制技術。

E-mail：liujiancheng1987＠126.com

趙宏志（197-8- ），男，副教授，博士，主要研究方向為無線信號處理。

E-mail：lyn＠uestc.edu.cn

全厚德（1963- ），男，教授，博士研究生導師，博士，主要研究方向為無線通信技術、指揮系統、通信設備性能測試。

E-mail：leopardfly222＠163.com

崔佩璋（197-4- ），男，副教授，博士，主要研究方向為信息與通信工程。

E-mail：cpz_zk＠163.com

唐友喜（1964-），男，教授，博士研究生導師，博士，主要研究方向為數字通信、擴頻通信（包括CCFD，OFDM）。

E-mail：tangyx＠uestc.edu.cn

孫慧賢（198-0- ），男，講師，博士，主要研究方向為指揮控制系統抗干擾技術。

E-mail：Ares_sun＠163.com

RF interference cancellation based on antennas coupling analysis for radios on the co-vehicle

LIU Jian-cheng1，ZHAO Hong-zhi2，QUAN Hou-de1，CUI Pei-zhang1，TANG You-xi2，SUN Hui-xian1
（1.Department of Information Engineering，Ordnance Engineering College，Shijiazhuang 050003，China；2.National Key Laboratory of Science and Technology on Communications，University of Electronic Science and Technology of China，Chengdu 611731，China）

The interference between military very high frequency（VHF）radios in the same vehicle is producing more trouble with the increasing complication of the tactical command and control system.A radio frequency（RF）interference cancellation method based on exploring the mutual near-field coupling between antennas，is proposed to cancel the mutual interference of radios on the co-vehicle.In addition，an analytical expression is derived to reflect the relationship between coupling calculation error and convergence time of the system.This method builds the near-field analysis model between transmitting and receiving antennas over one vehicle in advance，meanwhile，the mutual coupling and phase distortion are deduced.Then the calculation result is utilized to set the original parameters of the adaptive interference canceling chain，and efficiently cancel the RF interference.Finally，the simulations verify that the system convergence time is 30%less than that of the existing adaptive cancellation method，and prove the validity of the analytical expression reflecting how the coupling calculation error impairs system convergence time.

radio mutual-interference；near-field coupling；adaptive interference cancellation；convergence time

TN 911

A

10.3969／j.issn.1001-506X.2015.11.27

1001-506X（2015）11-2598-08

2014- 11- 07；

2015- 02- 17；網絡優先出版日期：2015- 05- 06。

網絡優先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150506.1148.002.html

國家高技術研究發展計劃（863計劃）（2014AA01A704，2014AA01A706，2015AA01A701）；國家自然科學基金（61531009，61271164，61471108，61201266，61501093）；國家科技重大專項（2014ZX03003001- 002）資助課題