瀝青混合料動態模量預估模型及試驗研究分析

陳 亮

(東莞市茶山鎮城鎮建設規劃辦公室，廣東 東莞 523380)

瀝青混合料動態模量預估模型及試驗研究分析

陳 亮

(東莞市茶山鎮城鎮建設規劃辦公室，廣東 東莞 523380)

采用性能試驗機(AMPT)對3種混合料的動態模量及相位角進行了測試，在對比分析了溫度及頻率對瀝青混合料的影響后，根據瀝青混合料的時間—溫度等效原理，通過非線性最小二乘法擬合得到瀝青混合料動態模量的主曲線，并參照國外的研究成果，得到了各動態模量的預估模型方程。

瀝青混合料，動態模量，相位角，主曲線，預估模型方程

瀝青混合料是一種粘彈性材料，受力狀況較為復雜[1]，目前，我國瀝青混合料試件試驗受力狀況大多還是靜態的[2]，這與實際的路面受力狀態有明顯的差別。由于瀝青路面在實際的環境中會受到多種因素的影響，比如在車輛行駛過程中，路面不僅會受垂直方向而來的振動沖擊，而且還會受水平方向的推移。因此，為了使試驗中的試件更接近于實際的受力狀態，動態復數模量的運用對路面設計體系中的重要性越來越明顯。國外早已將動態復數模量應用到路面設計體系中，并將其作為重要的參數進行路面設計，已經列入了路面設計指南中[3]。自1960年動態模量被提出以來，國外已經對動態模量有許多研究成果[4,5]。我國的科研院所也對其進行了相關方面的研究，但在試驗過程中試驗儀器、試驗時間以及試驗成本等因素往往會受到各種限制，較難獲得極限溫度或極限荷載頻率作用下的動態模量，研究還相對有限。目前，我國對動態模量室內試驗的標準規程還不夠深入，混合料在動態荷載作用下的力學響應的研究也較少。

本文采用目前國際上普遍使用的瀝青混合料性能試驗機(AMPT)對3種常用的瀝青混合料進行動態模量試驗研究，利用時溫等效原理來確定材料動態模量主曲線，通過分析不同溫度和不同頻率下的時溫等效方程中參數的變化規律，以及考慮瀝青混合料動態模量主要影響因素，來建立合適的動態復數預估模型，為以后進一步深入研究動態復數模量提供依據。

1 試驗方案設計

室內試驗采用3種我國常用瀝青混合料級配：AC-13，AC-16,AC-20，采用美國SHRP計劃中Superpave混合料設計方法(AASHTO M 323-07)來設計瀝青混合料，瀝青混合料設計空隙率為4%，3種級配目標級配中值見表1。本研究參照國內外的相關試驗結果，采用無圍壓的條件下，在5 ℃，20 ℃，35 ℃，50 ℃四個溫度，25 Hz，10 Hz，5 Hz，2 Hz，1 Hz，0.5 Hz，0.1 Hz七個頻率下進行試驗，按照低溫向高溫、高頻向低頻的先后順序去測得不同溫度和不同頻率下的3種混合料動態模量和相位角。

表1 3種級配的目標級配

試驗過程中，首先采用旋轉儀壓實成型φ150 mm×170 mm 的圓柱體試件，然后用取芯機鉆取φ100 mm×150 mm 的芯樣進行試驗[1]，測得芯樣的試驗參數指標見表2，鉆取芯樣樣圖見圖1。最后采用AMPT 試驗儀對試件施加半正矢波軸向壓應力試驗荷載，來測量試件在不同溫度、不同頻率條件下的動態模量及相位角。

表2 3種芯樣試驗參數

2 試驗結果及分析

根據上述試驗與測試的步驟，從AMPT上經計算可以直接得到混合料的動態模量和相位角，試驗結果分別見圖2，圖3。

由圖2，圖3可知，3種瀝青混合料的動態響應主要受溫度及頻率的影響而變動，具體如下：

隨著溫度的上升，混合料的動態模量呈逐漸減小的趨勢，同時減小的程度逐漸放緩，且在5 ℃和 20 ℃時相位角逐漸增大，在35 ℃和 50 ℃時，相位角逐漸減小。這是由于試驗溫度越高，瀝青混合料越軟，其粘彈性特征越為顯著；而且在高溫狀態下，混合料的動態模量受荷載頻率影響較小，而在常溫狀態下，瀝青混合料的動態模量受荷載頻率的影響較為顯著。隨著荷載頻率的降低，混合料的動態模量呈逐漸減小的趨勢，而相位角則起伏變化。說明在5 ℃和 20 ℃時瀝青混合料的相位角減小，試驗溫度越低時，表現出的粘彈性性質不明顯；在 35 ℃和50 ℃時瀝青混合料的相位角增大，主要是在高溫時，瀝青混合料越軟，粘彈性越為明顯，導致混合料的相位角增大。由上述溫度和頻率對混合料試驗的影響可知，兩者對動態模量及相位角的變化規律較為一致。

另外，3種混合料的動態模量在相同試驗條件下的變化規律基本相同，表明級配對混合料動態特性影響不大；從3種混合料的相位角變化上，除了在50 ℃的條件下AC-20比AC-13和AC-16大外，其他荷載頻率下的相位角變化規律也基本一致，表明粗級配混合料表現出的粘性較細級配混合料明顯。

3 動態模量主曲線及模型預估方程的確定

根據眾多研究表明，瀝青混合料的動態特性主要受溫度及荷載頻率的影響，對于很好地研究動態特性而言，確定混合料的動態模量主曲線至關重要。主曲線的確定，是利用動態模量和相位角，采用時溫等效原理通過平移，將所有不同溫度和荷載時間下的瀝青混合料的模量曲線疊加成一條在參考溫度下的光滑曲線。通過主曲線，可以對不易得到的那些低頻或高頻試驗條件下的力學性能進行評價。這曲線的確定過程中，移位因子的確定由比較常用的WLF經驗方程確定[6,7]，見式(1)：

(1)

其中，C1和C2為常數；Ts為參考溫度；T為單個試驗溫度；αT為參考溫度時的移位因子。

利用非線性最小二乘法擬合來實現移位因子的水平平移，然后得到西格莫德(Sigmoidal)函數：

(2)

其中，|E*|為瀝青混合料的動態模量；tγ為參考溫度下作用時間；δ為最小的動態模量；α為動態模量值的范圍；β,γ均為回歸參數[8]。

由于在我國路面設計體系中，設計彎沉值的標準測試溫度為20 ℃，且在用設計路面的厚度時選取路面材料20 ℃的模量為設計模量[9]，所以本研究按照時溫等效原理，以20 ℃為參考溫度。采用數值分析方法，在不同荷載頻率下擬合得到其各自的移位因子，并獲得動態復數模量主曲線。其中3種瀝青混合料的動態模量模型參數計算結果及擬合確定的主曲線分別見表3，圖4。

表3 3種瀝青混合料動態模量主曲線模型參數

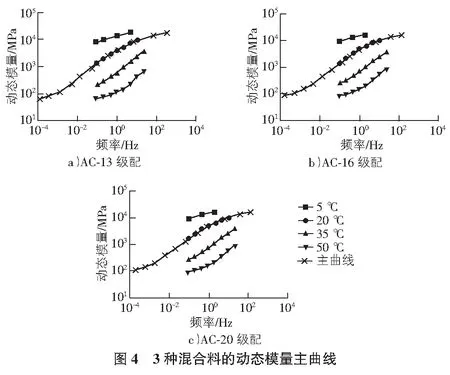
由圖4可知，3種瀝青混合料不同溫度條件下的動態模量經時溫等效原理平移變化后的值極其相近，說明西格莫德函數能較好地擬合混合料的動態模量主曲線。

對于動態模量的預估模型，國外有關學者給出了常用的動態模量經驗回歸公式[10-12]，見式(3):

E*=a×bc+d×fg+gT+hT×fi

(3)

其中，E*為動態模量；f為施加頻率；T為溫度;a，b，c，d，g，h均為擬合參數。

在式(3)的基礎上，利用SPSS數值軟件，對其參數進行擬合，進而對動態模量回歸公式進行擬合，算出參數后代入式(3)，最終獲得3種混合料的動態模量預估模型，分別如下：

1)AC-13預估模型方程如下：

E*=0.038×0.000 64(17.01-18.78×f0.001-0.347T+0.352T×f-0.001 6)

(4)

2)AC-16預估模型方程如下：

E*=1.035×0.002 61(32.89-33.65×f0.006-0.65T+0.45T×f-0.001 96)

(5)

3)AC-20預估模型方程如下：

E*=5.666×0.596(45.68-49.31×f0.004 6-0.035T+0.466T×f-0.010 1)

(6)

由上述得出的預估模型式(4)～式(6)均能很好地預測混合料的動態模量值，進而更好地表征混合料的粘彈特性及力學響應，也可作為預測國內常用瀝青混合料動態特性的參考，具有較強的適用性。

4 結語

對AC-13，AC-16和AC-20三種類型的瀝青混合料的動態模量進行測試，分析試驗過程中溫度和荷載頻率對動態特性的影響后，得出以下結論：1)隨著試驗溫度的上升，混合料的動態模量逐漸減小，同時減小程度逐漸放緩，且相位角呈現先增大后減小的變化趨勢。2)隨著試驗荷載頻率的降低，混合料的動態模量呈減小趨勢；而相位角則起伏變化，在低溫時相位角增大，而在高溫時相位角減小。3)3種混合料的動態模量和相位角在相同試驗條件下的變化規律基本上保持一致，表明級配類型對混合料動態特性影響不明顯。4)基于時溫等效轉換原理，利用最小二乘法擬合確定3類混合料的動態模量主曲線和移位因子表征瀝青混合料的粘彈性特征。5)利用SPSS數值分析方法，建立各混合料動態模量主曲線的Sigmoidal模型，為研究動態模量的預估提供有意義的參考。

[1] JTG E20—2011,公路工程瀝青及瀝青混合料試驗規程[S].

[2] 張肖寧.瀝青與瀝青混合料的粘彈性力學原理與應用[M].北京：人民交通出版社,2006.

[3] AASHTO.Standard Method of Test for Determining Dynamic Modulus of Hot-mix Asphalt Concrete Mixture[R].Washington DC:American Association of State Highway Transportation Officials,2005.

[4] THOMAS H.Using the Dynamic Modulus Test to Assess the Mix Strength of HMA [J].Public Roads,2001,64(6):6-8.

[5] DOUGAN C E.Dynamic Modulus Test Protocol Problems and Solution[R].Storrs:University of Connecticut,2003.

[6] Ferry J D.Viscoelastics properties of polymer [M].Hoboken: John Wiley and Sons Inc,1970.

[7] 黎 曉,梁乃興,陳 玲.瀝青混凝土動態模量及時—溫等效方程[J].長安大學學報(自然科學版),2014,34(3):35-40.

[8] PELLINEN T K, WITCZAK M W. Stress Dependent Master Curve Construction for Dynamic (Complex) Modulus[J].Journal of the Association of Asphalt Paving Technologists,2002(71):281-309.

[9] JTG D50—2006,公路瀝青路面設計規范[S] .

[10] 丁克良,沈云中,歐吉坤.整體最小二乘法直線擬合[J].遼寧工程技術大學學報(自然科學版),2010,29(1):44-47.

[11] CHOA Y H, PAPKB D H, HWANG S D. A predictive equation for dynamic modulus of asphalt mixtures used in Korea[J].Construction and Building Materials,2010,24(4):513-519.

[12] 馬 翔,倪富建,陳榮生.瀝青混合料動態模量及模型預估[J].中國公路學報,2008,1(3)：35-39.

The dynamic modulus prediction model and experimental research analysis on asphalt mixture

Chen Liang

(DongguanChashanTownPlanningOffice,Dongguan523380,China)

Used AMPT testing dynamic modulus and phasing degree of 3 mixtures to do further study on their dynamic performance when used. After the comparative analysis of the effects of temperature and frequency on asphalt mixture, based on the equivalence principle of time-temperature on mixtures, that gained the asphalt mixtures’ dynamic modulus principal curve by using nonlinear least square method. At last, results gained the forecasted-model equations of dynamic modulus by referring to the foreign research.

asphalt mixture， dynamic modulus， phasing degree， master curve， forecasted-model equations

2015-01-23

陳 亮(1983- )，男，碩士，工程師

1009-6825(2015)10-0120-03

TU535

A