氯離子侵蝕作用下扶壁式擋土墻極限承載能力
楊 關
(中國電力工程顧問集團西南電力設計院,四川 成都 610021)
氯離子侵蝕作用下扶壁式擋土墻極限承載能力
楊 關
(中國電力工程顧問集團西南電力設計院,四川 成都 610021)
以某變電站工程扶壁式擋土墻設計案例為對象,根據朗肯土壓力理論計算擋土墻后土側壓力,研究在設計使用期內的氯離子擴散及鋼筋銹蝕過程,并進行了獨立斷面和整體結構的極限承載能力研究,為其結構設計和優化提供了依據。
扶壁式擋土墻,鋼筋混凝土結構,極限承載能力,土壓力,數值模擬
0 引言
鋼筋混凝土扶壁式擋土墻多用于支護高填方路段邊坡,其耐久性能是結構設計首要考慮的問題。當混凝土表面暴露在自然環境中時,氯鹽、水等能通過表面微孔侵入其中,進一步造成內部的鋼筋發生銹蝕,使混凝土結構承載能力發生退化。本文根據Fick定律,以混凝土侵蝕模型和鋼筋銹蝕模型為基礎,通過有限元數值模擬方法模擬鋼筋混凝土構件的材料退化過程[1],從而得到構件的結構性能和工作狀態[2]。
本文介紹了鋼筋混凝土結構耐久性數值模擬的基本原理和相應的數值軟件工具,并以某變電站工程扶壁式擋土墻的扶壁部分為研究對象,評價該鋼筋混凝土結構的扶壁部分在鋼筋銹蝕狀態下的斷面和整體結構承載能力。
1 工程概況
本扶壁式擋土墻位于某變電串補站旁填方區。因場地限制,對填方深度較深地段采用鋼筋混凝土扶壁式擋土墻進行支護。扶壁式擋土墻設計如圖1所示。配置鋼筋包括φ40,φ12的主筋。墻體材料采用現澆C30強度混凝土,主筋為HRB400。

2 數值模擬
2.1 計算理論
氯離子侵蝕下的鋼筋混凝土構件耐久性退化過程是始于氯離子從混凝土表面侵入混凝土的孔隙結構,進而造成混凝土內部的鋼筋發生銹蝕,鋼筋銹蝕的同時引起混凝土銹脹開裂及強度下降,進而導致混凝土構件承載能力下降。本文以該過程為基礎,介紹了針對這一過程中的關鍵物理模型,從而實現混凝土構件的承載能力評價。
氯離子在混凝土中的擴散問題一般認為等效于離子在液體中的擴散問題。液體中的離子擴散一般采用Fick第二定律來描述,其表達式為:
(1)
式中:C——混凝土中自由離子濃度,kg/m3;
D——離子擴散系數。
鋼筋平均銹蝕速率是指在給定環境中鋼筋整個截面的平均銹蝕速率,與局部氯離子濃度、鋼筋材料以及鋼筋直徑、肋紋特征等指標有關。鋼筋平均銹蝕模型采用由BIONDINI提出的線性退化模型,使用由涂熙[1]擬合得到的線性比例系數,鋼筋線性銹蝕模型的表達式為:
?δm/?t=0.004 6·C(x,t)
(2)
式中:δm——鋼筋的平均銹蝕度;
?δm/?t——鋼筋瞬時平均銹蝕速率;
C(x,t)——混凝土內空間坐標為x處在時間t時刻的氯離子濃度。
表層混凝土因銹脹開裂后導致該部分混凝土的強度顯著下降。為了簡化分析步驟,假定該部分混凝土開裂后不參與工作,將原有混凝土截面扣除后得到縮小的混凝土截面,進而得到偏安全的計算值。
2.2 假設條件和計算參數
擋土墻的扶壁部分主要承受水平方向的土壓力,在其結構豎向僅承受自身的自重。因此本文按規范將扶壁部分簡化為純彎構件,分析扶壁部分各個關鍵斷面及擋墻整體的彎曲承載能力。結構計算考慮混凝土和鋼筋的材料非線性。
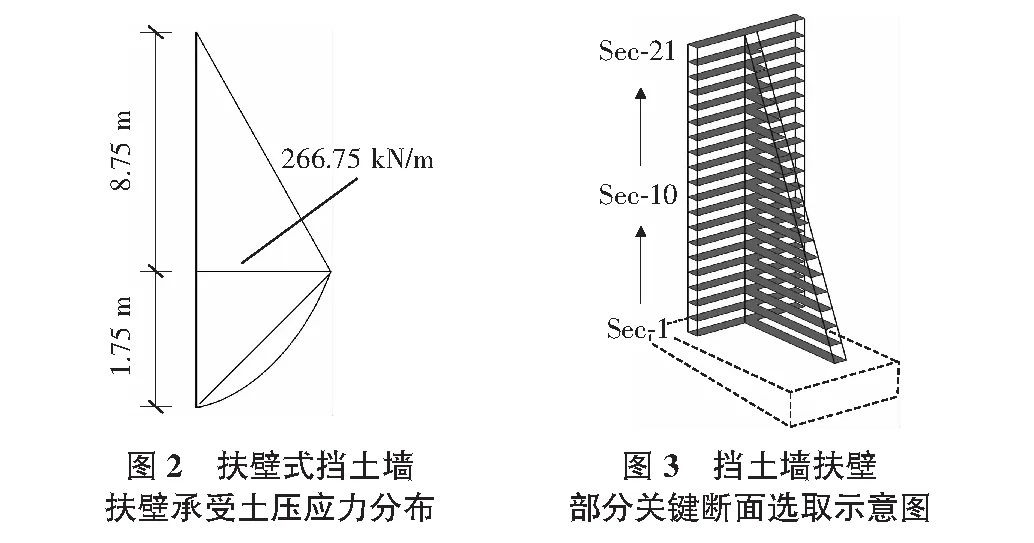
土壓力:擋土墻主要承受的外部荷載為側向土壓力。工程上采用的兩種土壓力計算經典理論為庫侖理論(Coulomb theory)和朗肯理論(Rankine theory)[5]。其中,庫侖理論計算比較簡便,且能適用于各種復雜邊界的情況,其計算精度能滿足工程需要。根據本文背景工程的勘測及設計資料,墻后填土為砂類土,內摩擦角標準值為φk=35°,重度γ=20.5 kN/m3,填土水平且無地下水。結構設計考慮為墻后靜止土壓力,靜止土壓力系數K0=1-sin35°=0.426。
因此計算可得扶壁土壓力最大值為:
qmax=ln(H1-ln/2)K0=266.75 kN/m
(3)
結構設計考慮墻后靜止土壓力分布按圖2所示取值。其中,最大值以下部分的實際土壓力分布曲線為凸曲線,為計算方便將其簡化為圖中虛線所示直線。
2.3 計算模型和邊界條件
扶壁式擋土墻的耐久性評價工作分為兩個部分:首先按構件斷面為單位進行氯離子擴散模擬和鋼筋銹蝕評價,其次進行結構承載能力評價,并比較關鍵斷面承載力和整體承載力的差異。評價扶壁式擋土墻共選取21個關鍵斷面進行截面抗彎承載能力分析(見圖3)。
針對扶壁式擋土墻的擴散模擬過程設定為100年。混凝土中自由氯離子擴散系數取2×10-13m2/s。氯離子邊界條件按文獻[6]將扶壁式擋土墻氯離子邊界濃度設定為0.41%。邊界條件設置在擋土墻與外部環境直接接觸的表面上。
2.4 計算結果
關鍵斷面首先進行初步分塊,再以四邊形單元進行映射網格劃分以形成規整的標準網格。數值模擬計算得到混凝土中各點的氯離子相對濃度,即各點濃度值與邊界條件上的數值之比(如圖4所示)。
在全截面侵蝕濃度分布的基礎上,根據截面內每根鋼筋的位置,插值得到鋼筋位置侵蝕濃度的演變歷程,如圖5所示。引入實際氯離子濃度邊界條件后,計算得到鋼筋在分析周期內的銹蝕歷程(見圖6)。

通過材料非線性迭代計算,得到擋土墻各關鍵斷面的彎曲承載力隨時間的退化歷程(見圖7)。計算結果表明斷面承載力的整體退化過程呈先平緩后加速的下降趨勢。
扶壁式擋土墻主要受力在其構件受彎方向,因此簡化其側向的網格劃分,保證縱向的網格質量,模型狀態如圖8所示。
針對整體結構的加載模式為按比例將墻后標準土側壓力放大至結構失效,從而得到擋土墻整體結構進入材料非線性階段的極限承載能力,定義此時的放大比例為該荷載放大系數,其隨時間的演變歷程如圖9所示。
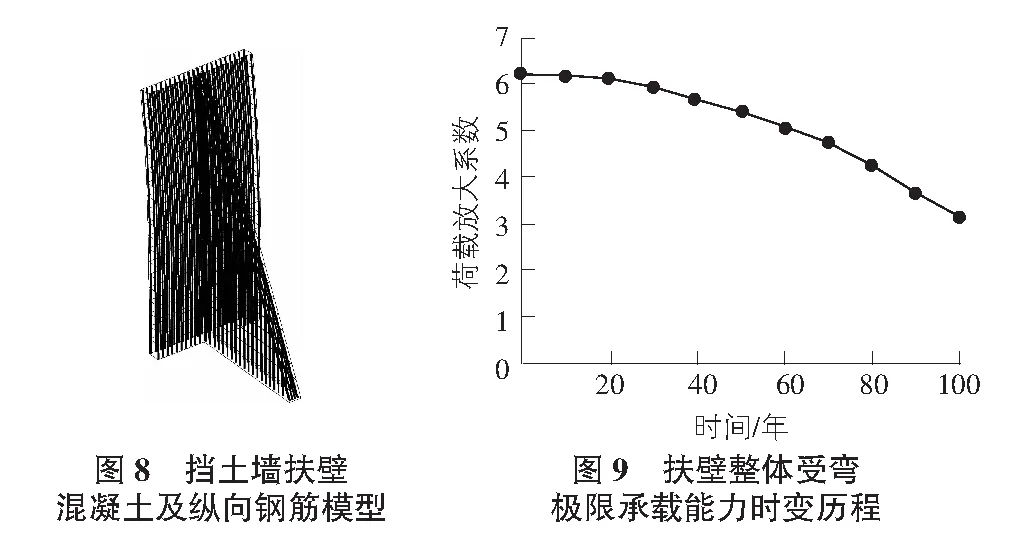
以受彎承載能力安全系數的初始值為基數,可得到整體結構在各時點的極限承載能力相對值,并將該值與關鍵截面承載力相對值進行比較,如圖10所示。由于斷面構造和邊界條件的不同,斷面受拉區鋼筋對外部侵蝕的敏感性不同,擋土墻頂部斷面承載力的退化發展比底部斷面較快。

3 結論和建議
本文介紹了采用數值模擬手段評價扶壁式擋土墻的結構承載能力的方法。外部氯離子侵蝕作用下,扶壁式擋土墻結構在使用期內的承載能力為逐步降低規律,相應的安全儲備下降。由于邊界條件不同,扶壁式擋土墻不同位置斷面的承載能力退化趨勢不同,根據不同位置承載能力的退化速率不同,建議增加頂部斷面的混凝土保護層厚度。
[1] 涂 熙.鋼筋混凝土橋梁氯離子侵蝕及其結構耐久性數值分析方法[D].上海:同濟大學,2012.
[2] Biondini F.,Bontempi F.,Frangopol D.M.,et al.Cellular Automata Approach to Durability Analysis of Concrete Structures [J].Journal of Structural Engineering,ASCE,2004,130(11):1724-1737.
[3] Zhang,R.,Castel,A.Concrete cover cracking with reinforcement corrosion of RC beam during chloride-induced corrosion process[J].Cement and Concrete Research,2010,40(3):415-425.
[4] Sanchez,P.J.,Huespe,A.E.Mesoscopic model to simulate the mechanical behavior of reinforced concrete members affected by corrosion[J].International Journal of Solids and Structures,2010,47(5):559-570.
[5] 顧慰慈.擋土墻土壓力計算 [M].北京:中國建材工業出版社,2001.
[6] 何立坤.氯離子侵蝕作用下鋼筋混凝土橋梁耐久性退化全過程數值模擬[D].天津:天津大學,2011.
The ultimate bearing capacity of buttressed retaining wall under the chloride ion erosion
YANG Guan
(SouthwestElectricPowerDesignInstitute,ChinaPowerEngineeringConsultingGroup,Chengdu610021,China)
Taking the buttressed retaining wall design case of a transformer substation engineering as the object, according to the Rankine soil pressure theory calculation of last earth pressure of retaining wall, researched the chloride ion diffusion and reinforced corrosion process in design trial period, and researched the ultimate bearing capacity of independent section and overall structure, provided basis for structure design and optimization.
buttressed retaining wall, reinforced concrete structure, ultimate bearing capacity, soil pressure, numerical simulation
2014-11-22
楊 關(1982- ),男,工程師
1009-6825(2015)04-0039-03
TU476.4
A

