非合作機動目標交會的相對位置控制*

徐李佳，胡 勇

(1.北京控制工程研究所,北京 100190; 2.空間智能控制技術重點實驗室,北京 100190)

?

非合作機動目標交會的相對位置控制*

徐李佳1,2，胡 勇1,2

(1.北京控制工程研究所,北京 100190; 2.空間智能控制技術重點實驗室,北京 100190)

研究目標航天器存在機動的情況下追蹤航天器與目標航天器的交會問題.只利用兩航天器之間的相對位置測量信息，考慮目標機動、外部干擾以及狀態耦合，提出一種改進的特征壓縮方式并建立相應的解耦特征模型，基于該特征模型設計解耦的自適應控制方法實現追蹤航天器與機動目標航天器的交會.仿真結果驗證了算法的有效性，并表明其優于傳統的PD控制方法.

交會對接;機動目標;非合作目標;特征模型;自適應控制

0 引 言

空間交會對接技術(RVD，rendezvous and docking)是航天工程中的一項關鍵技術[1].一般情況下，目標航天器為合作目標，也就是說目標航天器配合追蹤航天器來完成交會對接任務， 如保持自身軌道、姿態穩定.然而，隨著空間任務需求的增加，研究非合作目標的交會對接技術是一個重要的發展趨勢.所謂非合作目標是指目標航天器不主動配合追蹤航天器的交會對接要求，主要分為兩種情況：一種是目標航天器姿態不主動配合交會對接任務的情況[2-4]，如姿態不可控制的失控衛星或小行星等； 另一種是目標航天器軌道信息未知[5]甚至自身機動[6]而不配合與追蹤航天器交會對接的情況，如在交會過程中同時需要躲避空間碎片的機動目標航天器或者主動逃避交會的敵方航天器等.本文主要針對第二種目標航天器存在機動的情況進行研究，對未來復雜的航天任務和空間攻防任務具有重要的經濟和軍事價值.

針對在任意橢圓軌道上運行的目標航天器，通常可用T-H方程來近似描述追蹤航天器與目標航天器之間的相對運動，文獻[7-9]等基于T-H方程設計交會控制方法，但沒有考慮兩航天器所受到的外界干擾，如羽流干擾、太陽光壓、地球攝動、位置姿態耦合等，本文將考慮實際交會環境中的這些干擾項.由于目標航天器為非合作對象且存在機動，能用于交會控制的測量信息非常有限，本文只利用兩航天器的相對位置測量信息，設計控制方法實現交會.考慮到實際的控制系統為采樣系統，因此本文基于特征模型理論進行特征建模和控制器設計.

所謂特征模型[10]是指根據對象的動力學特征、環境特征和控制性能要求相結合而建立的模型.基于特征模型的自適應控制方法主要有全系數自適應控制[11]，黃金分割自適應控制[12]，已成功應用于多個航天任務中，如神舟飛船與天宮實驗室的交會對接任務[13]，嫦娥五號飛船的返回再入任務等.然而，針對本文討論的目標航天器存在機動的情況，在對其進行特征建模的過程中，考慮到目標航天器的機動力及各種外界干擾項并非為系統狀態的函數，因此以往的特征壓縮方式不能完全適用.同時考慮到兩航天器交會的相對運動各個軸分量之間存在耦合，從控制的角度出發，解耦控制更為簡單實用，為此本文提出一種改進的特征壓縮方式，從而得到三軸解耦的特征模型，并基于特征模型設計自適應控制方法實現兩航天器的交會.最后通過數學仿真驗證本文所提方法的有效性，并與傳統PD控制進行比較.

1 相對運動描述

考慮目標航天器所在軌道為一般的橢圓軌道， 為建立追蹤航天器與目標航天器之間的相對運動， 首先定義如下兩個坐標系：(1)地球慣性坐標系: 以地心為原點，xI軸和yI軸位于赤道平面內且xI軸從地心指向春分點，zI軸垂直于赤道平面且朝北，yI軸滿足右手正交； (2)目標軌道坐標系: 以目標航天器質心為原點，xo軸和zo軸位于軌道平面內且zo軸指向地心，xo軸指向速度方向且垂直zo軸，yo軸垂直于軌道平面，滿足右手正交.兩坐標系關系如圖1所示，其中rt，rc分別為地心指向目標航天器和追蹤航天器的位置向量，r由目標航天器指向追蹤航天器的位置向量.

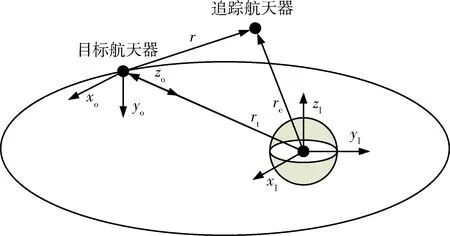
圖1 相對運動坐標系Fig.1 Coordinate system for the relative motion

下面建立兩航天器的相對運動方程.在地球慣性坐標系下，目標航天器和追蹤航天器的運動方程分別為

(1)

(2)

式中：μ為地心引力常數，mt和mc分別為目標航天器和追蹤航天器的質量，且隨著推進劑燃料的消耗而變化，Ft為目標航天器的未知機動力，Fc為追蹤航天器的可控推力，Ftd和Fcd分別為目標航天器和追蹤航天器所受的外界干擾力，如羽流干擾、太陽光壓、地球攝動、位置姿態耦合等.

兩航天器在慣性坐標系下的相對位置關系為

r=rc-rt

(3)

將其轉換到目標軌道坐標系中，有

(4)

其中ω為目標航天器的軌道角速度.

將方程中的向量表示成

(5)

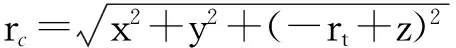
那么可得到目標軌道坐標系中各個軸對應的方程

(6)

(7)

(8)

式中：Fcdx,Fcdy,Fcdz和Ftdx,Ftdy,Ftdz分別為追蹤航天器和目標航天器所受外界干擾力的3個分量，Ftx,Fty,Ftz分別為非合作目標航天器未知機動力的3個分量，Fcx,Fcy,Fcz分別為追蹤航天器可控推力的3個分量.

2 特征建模

根據上節給出的相對運動方程(6)～(8)，可以看出三軸之間互相耦合，同時還帶有與狀態無關的不確定項(外界干擾和目標機動力).一般在工程應用中，針對各個主軸的解耦控制使用較多，具有更高的實用價值.因此本文將針對該類三軸耦合及帶有不確定項的對象，建立一種解耦的特征模型，使各個軸能夠獨立設計控制器.

下面首先分析相對運動方程(6)～(8)，可以看出各個主軸對應方程的描述形式基本一致，為便于后續分析，將其寫為如下統一形式

δi(t)+b(t)ui(t)

(9)

接下來，針對方程(9)描述的各個軸的相對運動進行特征建模.由于工程中為采樣系統，那么首先對式(9)進行離散化處理.采用歐拉離散化方法[11]，得到各軸的離散形式為

ξi(k+1)=αi1(k)ξi(k)+αi2(k)ξi(k-1)+

βi(k)ui(k)+qi(k)

(10)

其中ξi(k)表示k時刻ξi的采樣值，參數αi1(k)=2+h2ai(k),αi2(k)=-1,βi(k)=h2b(k),h為采樣周期，qi(k)為k時刻總的不確定性項，由當前主軸與其他兩個主軸的耦合項和擾動項組成，即

qi(k)=h2(gi(k)+δi(k)).

(11)

可見，若要得到各軸解耦的模型，那么必須對上述總的不確定項進行處理.

在以往的特征建模過程中，通常將系統的不確定項壓縮到幾個特征參量和特征變量中，但前提是該不確定項為狀態的函數，且滿足當特征變量ξi(k)→0的時候不確定項qi(k)→0，那么可以得到特征模型的標準形式.然而，針對本文這種情況是不適用的，因為不確定項qi(k)并非為狀態ξi(k)的函數，也就是說當ξi(k)→0的時候不能滿足qi(k)→0，若直接采用特征模型的標準形式，那么標準形式的特征模型是滿足ξi(k)→0的時候ui(k)→0的，而原系統ξi(t)→0的時候不能得到ui(t)→0，因為不確定項無法消除，因此標準形式的特征模型與原系統無法等價.為解決該情況下的特征建模，本文將對特征壓縮方式進行如下改進.

首先，定義一個集合

(12)其中ηi>0.接下來，將離散模型分兩種情況進行處理：

第一種情況:ξi(k)∈RΩi.也就是說在這種情況下，被控對象的實際采樣輸出值ξi(k)遠離零點，那么方程(10)中的不確定項qi(k)可以直接壓縮到特征參量和特征變量中，即

(13)

其中3個特征參量為:

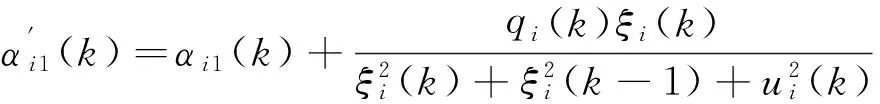
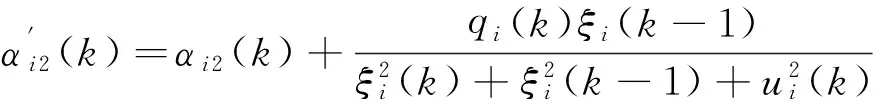
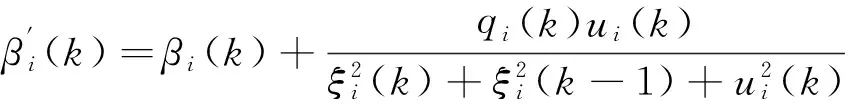
且上述特征參量的界滿足

(14)

其中ε1j(h)>0,j=1,…,4為采樣周期h的函數，且隨著采樣周期減小而減小.

第二種情況: ξi(k)∈Ωi.在這種情況下被控對象的實際采樣輸出值ξi(k)在零點附近，若依舊按照第一種情況的壓縮方式進行壓縮，則可能會出現特征參量特別大甚至奇異的情況，因此在這種情況下上述方式不再適用，本文為此做如下處理：首先定義一個新的特征變量ξi(k)，滿足

(15)

其中di為常數，一般取di>ηi.接下來，將方程(10)中的不確定項qi(k)壓縮到新的特征參量和特征變量中，得到如下新的特征模型形式

(16)

其中3個新的特征參量為:

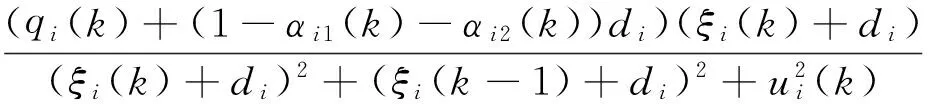
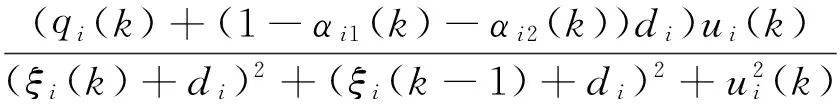
且上述特征參量的界滿足

(17)

其中ε2j(h)>0,j=1,…,4為采樣周期h的函數，且隨著采樣周期減小而減小.

通過比較式(13)和式(16)，可以看出在上述兩種情況下特征模型的描述形式一致, 那么寫成如下統一形式：

(18)

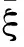
(1)當ξi(k)∈RΩi時，

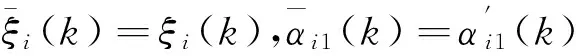
(2)當ξi(k)∈Ωi時，

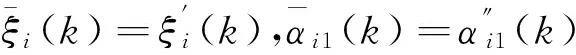
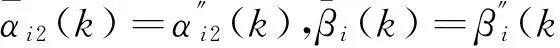
可見，由式(18)給出的特征模型為各個主軸的統一形式，接下來將基于各軸對應的特征模型設計控制器.

3 控制器設計

由于各個主軸的特征模型相互解耦，因此可獨立設計控制器.解耦控制相比耦合的多輸入多輸出控制簡單可靠，因此更適合工程應用.

針對已建立的各個軸的特征模型統一形式，設計解耦的自適應控制器.考慮跟蹤控制，設計的控制器由維持跟蹤控制律和黃金分割控制律兩部分組成，即

ui(k)=ui1(k)+ui2(k)

(19)

其中ui1(k)為維持跟蹤控制律

(20)

ui2(k)為黃金分割反饋控制律

(22)

(22)

(23)

其中Di(Ωi,ξi(k))為死區函數,定義為

(24)

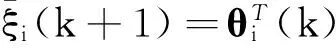
(25)

(26)

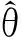
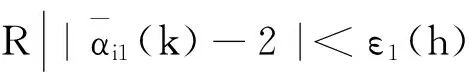
(27)

其中εj(h),j=1,…,4為特征參數的界,滿足 ε1(h)=min{ε11(h),ε21(h)}， ε2(h)=min{ε12(h),ε22(h)}， ε3(h)=max{ε13(h),ε23(h)}， ε4(h)=min{ε14(h),ε24(h)}，min和max分別表示最小最大值.

4 仿真研究

為了驗證文中所提算法的有效性，下面給出一個非合作機動目標交會對接的數學仿真例子.

首先假設目標航天器所在的軌道為一般的橢圓軌道，近地點距離地球表面200 km，軌道偏心率為0.7，初始真近點角為-150°，軌道傾角為30°，升交點赤經為60°，近地點幅角為0°.假設追蹤航天器與目標航天器的初始相對位置為[x(0),y(0),z(0)]=[-20,0,5] m，期望的末端相對位置為[x(tf),y(tf),z(tf)]=[-0.01,0,0] m，交會時間tf設為300 s.考慮目標航天器為非合作對象且存在機動，假設其機動力轉換到目標軌道坐標系中3個軸方向上的分量為[Ftx，Fty，Ftz]=[10sin(0.08t+π/6)，4sin(0.05t+π/4)，8sin(0.1t+π/2)] N.假設目標航天器的質量為200 kg，追蹤航天器的質量為100 kg，并考慮±10%的質量變化.同時考慮追蹤航天器的推力能力，假設追蹤航天器最大可控推力不超過5 N.

針對機動目標航天器的交會控制問題，只利用追蹤航天器通過相對敏感器測量得到與目標航天器之間的相對位置信息，采用本文提出的基于特征模型的自適應控制方法(ACCM)控制追蹤航天器交會逼近至非合作目標航天器，并與傳統的PD控制方法進行比較.

圖2為兩航天器相對距離的變化曲線，其中虛線和實線分別用于表示采用PD控制和基于特征模型的自適應控制下的相對距離變化，兩子圖分別為兩種控制方法下在交會末端最后100 s的細節圖.可以看出，采用基于特征模型的自適應控制方法的控制效果明顯優于傳統的PD控制，在控制力相當的前提下，交會精度較高.圖3為目標軌道坐標系中相對位置變化曲線，比較兩種控制方法可以看出，解耦控制不僅使用簡單而且控制效果理想，各軸控制精度都優于PD控制.圖4為采用基于特征模型的自適應控制方法在目標軌道坐標系中的控制推力，滿足推力限制要求.

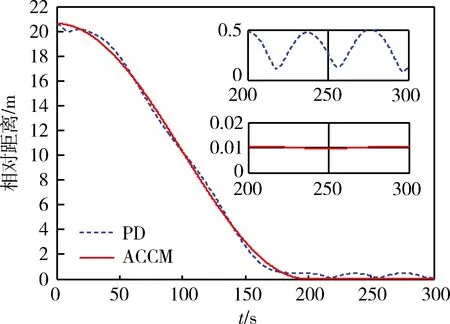
圖2 相對距離Fig.2 Relative distance

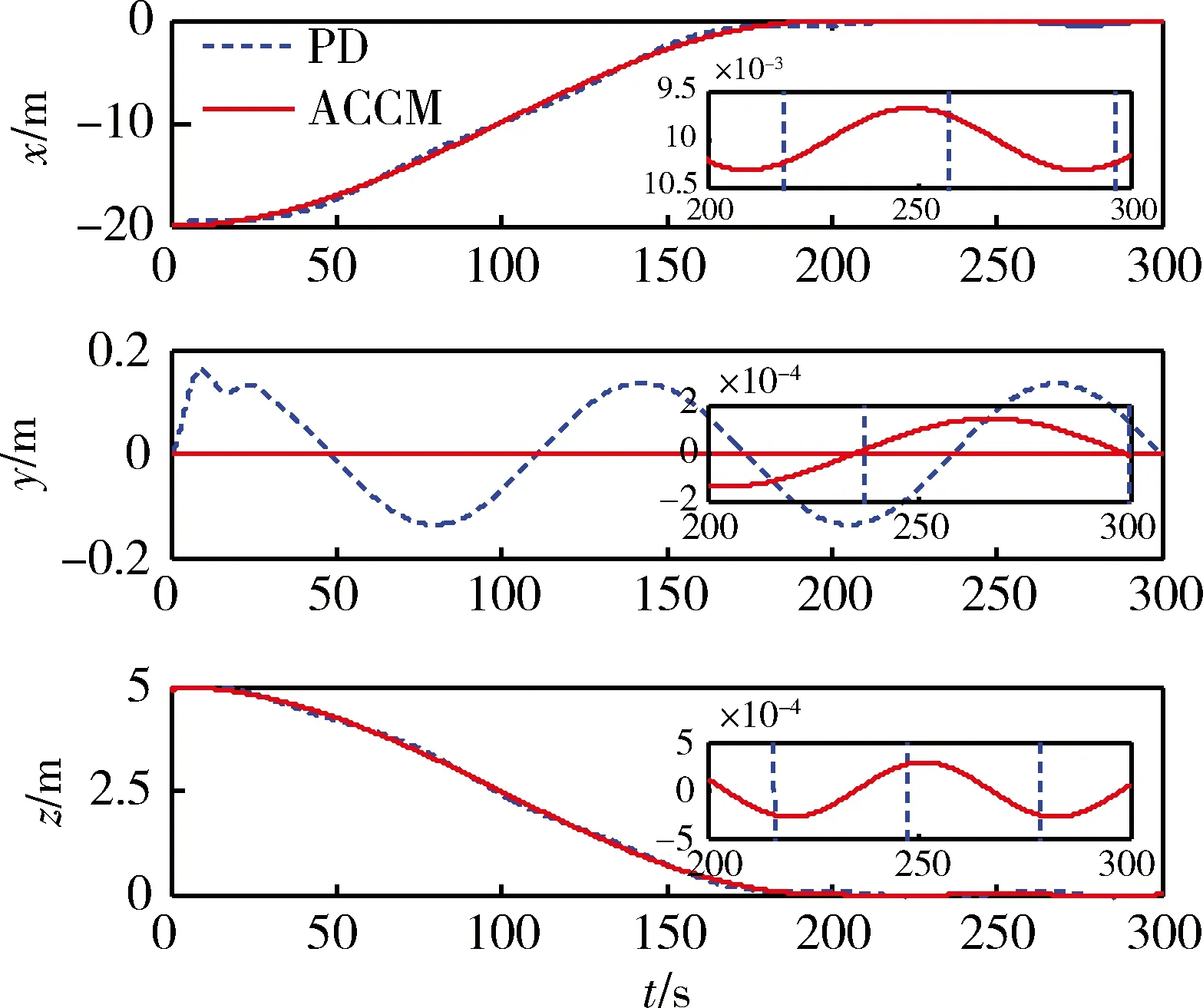
圖3 相對位置Fig.3 Relative position

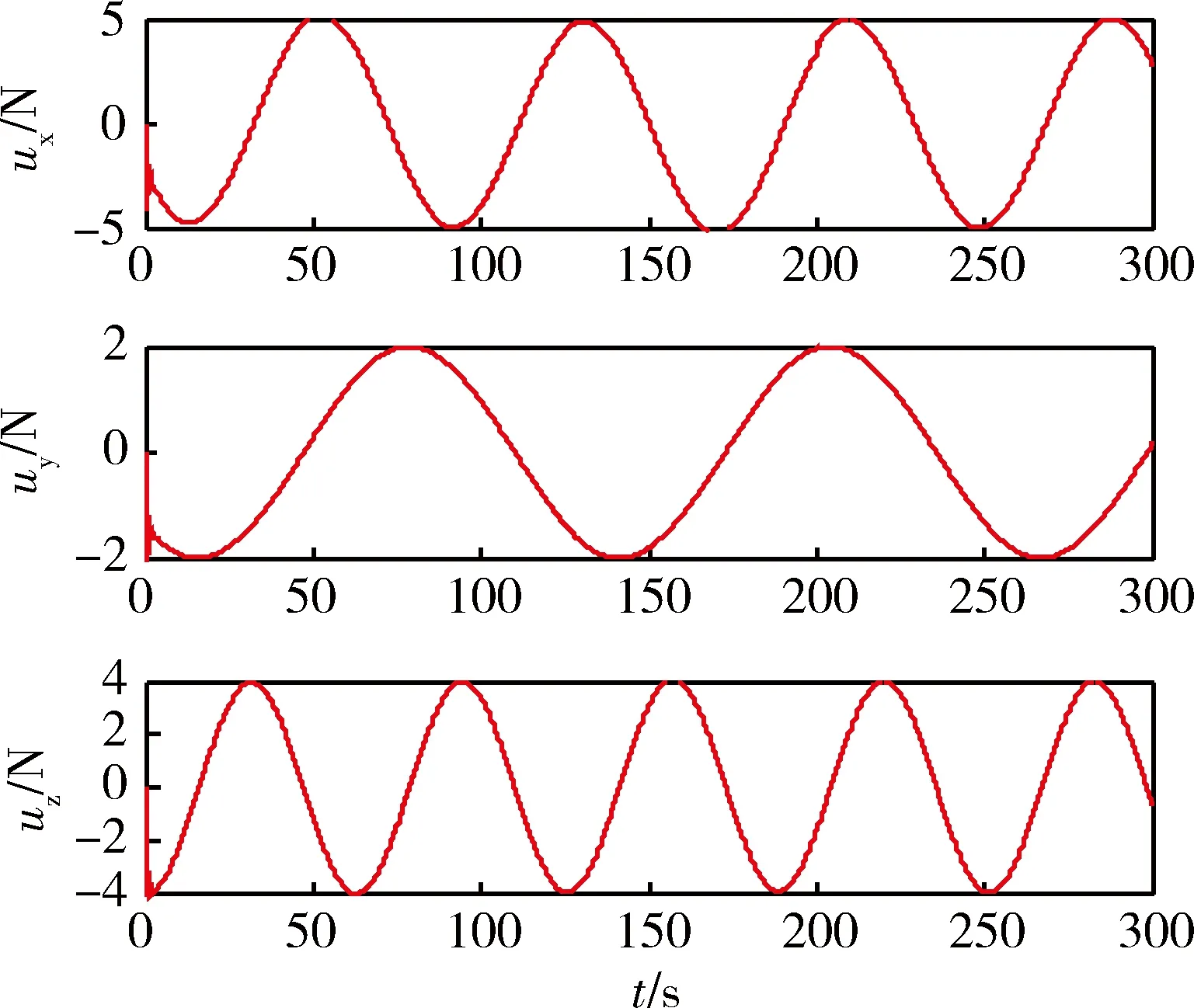
圖4 追蹤航天器的控制推力Fig.4 Control input of the chaser spacecraft

5 結 論

本文針對一類非合作機動目標交會問題， 設計一種基于特征模型的自適應控制方法實現追蹤航天器與目標航天器的交會.首先在特征建模方面，由于存在與系統狀態無關的項，因此不能進行簡單的壓縮，本文提出一種改進的特征壓縮方式，使之能將其壓縮到可辨識的特征參量和已知的特征變量中，得到解耦的特征模型.其次，基于上述特征模型和壓縮條件，設計解耦的自適應控制器.在數學仿真中，驗證本文所提方法的有效性及優越性.

[1] 朱仁璋. 航天器交會對接技術[M]. 北京: 國防工業出版社, 2007.

[2] BOYARKO G, YAKIMENKO O, ROMANO M. Optimal rendezvous trajectories of a controlled spacecraft and a tumbling object[J]. Journal of Guidance, Control, and dynamics, 2011, 34(4): 1239-1252.

[3] MATSUMOTO S, DUBOWSKY S, JACOBSEN S, et al. Fly-by Approach And Guidance For Uncontrolled rotating satellite capture[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Washington D.C.: AIAA, 2003.

[4] 胡勇, 徐李佳, 解永春. 針對失控翻滾目標航天器的交會對接控制[J]. 宇航學報, 2015, 36(1): 47-57. HU Y, XU L J, XIE Y C. Characteristic model based control in rendezvous and docking with a tumbling target spacecraft[J]. Journal of Astronautics, 2015, 36(1):47-57.

[5] XU L, HU Y, JIANG T. Autonomous rendezvous control and determination of unknown target orbit[C]//Proceedings of the 19thIFAC World Congress. Cape Town:IFAC, 2014, 19(1): 9709-9714.

[6] ZHOU Z. Trajectory control of rendezvous with maneuver target spacecraft[C]//AIAA/AAS Astrodynamics Specialist Conference. Washington D.C.: AIAA, 2012.

[7] SINGLA P, SUBBARAO K, JUNKINS J L. Adaptive output feedback control for spacecraft rendezvous and docking under measurement uncertainty[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(4): 892-902.

[8] ZHOU B, LIN Z, DUAN G. Lyapunov differential equation approach to elliptical orbital rendezvous with constrained controls[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2): 345-358.

[9] LU S, XU S. Adaptive control for autonomous rendezvous of spacecraft on elliptical orbit[J]. Acta Mechanica Sinica, 2009, 25(4): 539-545.

[10] 吳宏鑫, 胡軍, 解永春. 基于特征模型的智能自適應控制[M]. 北京: 中國科學技術出版社, 2009.

[11] WU H, HU J, XIE Y. Characteristic model-based all-coefficient adaptive control method and its applications[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C: Applications and Reviews, 2007, 37(2): 213-221.

[12] 孟斌, 吳宏鑫. 黃金分割控制的收斂性和穩定性研究[J]. 宇航學報, 2009, 30(5): 2128-2132. MENG B, WU H X. Convergence and stability of the golden-section control[J]. Journal of Astronautics, 2009, 30(5): 2128-2132.

[13] 胡軍, 解永春, 張昊, 等. 神舟八號飛船交會對接制導、導航與控制系統及其飛行結果評價[J]. 空間控制技術與應用, 2011, 37(6): 1-5. HU J, XIE Y C, ZHANG H, et al. Shenzhou-8 spacecraft guidance navigation and control system and flight result evaluation for rendezvous and docking[J]. Aerospace Control and Application, 2011, 37(6): 1-5.

Control for Relative Position of Spacecraft Rendezvous with aNon-Cooperative Maneuver Target

XU Lijia1,2, HU Yong1,2

(1.Beijing Institute of Control Engineering, Beijing 100190， China; 2.Science and Technology on Space Intelligent Control Laboratory, Beijing 100190, China)

This paper discusses the problem of rendezvous with a maneuver target spacecraft. Considering the maneuvers of the target spacecraft, as well as the external disturbance forces and the coupled states, a modified compress method is proposed and applied to establish the decoupled characteristic model based on the measurements of relative position. Then, a decoupled adaptive control method based on the characteristic model is presented to achieve the rendezvous of the two spacecraft. Finally, the simulation results demonstrate the effectiveness of the proposed method, and indicate that the method is better than the traditional PD control.

rendezvous and docking; maneuver target; non-cooperative target; characteristic model; adaptive control

*國家自然科學基金資助項目(61333008,61304027)和國家重點基金研究發展計劃(973)資助項目(2013CB733100).

2015-05-19

V448

A

1674-1579(2015)06-0013-06

10.3969/j.issn.1674-1579.2015.06.003

徐李佳(1987—),男，博士研究生，研究方向為航天控制；胡 勇(1982—)，男，工程師，研究方向為航天器控制理論與控制工程.