跨座式關節型道岔梁靜、動力學及疲勞壽命分析

王智祥，朱 明，張繼祥

(1.重慶交通大學 機電與汽車工程學院，重慶400074；2.重慶交通大學 重慶市特種船舶數字化設計與制造工程技術研究中心，重慶 400074)

?

跨座式關節型道岔梁靜、動力學及疲勞壽命分析

王智祥1,2，朱 明1，張繼祥1,2

(1.重慶交通大學 機電與汽車工程學院，重慶400074；2.重慶交通大學 重慶市特種船舶數字化設計與制造工程技術研究中心，重慶 400074)

采用ANSYS Workbench軟件，對關節型五開道岔梁的3號段進行了靜強度、模態及疲勞壽命分析。分析得到：道岔梁在靜載荷作用下的等效應力最大值是52.44 MPa，小于材料的屈服強度極限；變形最大處在梁的中上部，約0.29 mm；存在明顯的應力集中點，發生在焊接位置；1階振型固有頻率值約為51 Hz；道岔梁疲勞壽命仿真結果是49.6 a。研究表明：道岔梁在靜載作用下的強度滿足使用要求；模態分析中前3階振型的變形位置與靜強度分析顯示的變形區域重合，該處需加強剛度；道岔梁疲勞壽命符合鋼結構25 a的壽命設計要求。

橋梁工程；道岔梁；模態分析；強度

0 引 言

跨座式單軌鐵路的道岔有多種形式，按照其結構組成與轉轍后的形態可分為關節型道岔和關節可撓型道岔。其中關節型道岔又分為單開、對開、三開、五開、單渡線、雙渡線、交叉渡線等型式[1]。筆者重點研究關節型五開道岔梁，它是跨座式單軌交通系統中的基礎設施，是一種典型的焊接鋼結構。

楊佑發，等[2]研究了重慶輕軌的箱型鋼軌道梁的動力特性，對軌道梁的安全監控和狀態評估提供了必要信息；時瑾[3]對磁浮軌道梁進行了動力響應分析，對比了整體軌道梁在力學性能與動態性能上的優越性；牛均寬[4]對跨座式關節型道岔梁進行了有限元靜力學初步分析，通過試驗驗證了有限元分析的正確性；李振華[5]對跨座式單軌平移式道岔梁進行了靜、動力學分析；顧行濤[6]主要對磁懸浮道岔梁進行了動力學及疲勞壽命的分析。迄今，國內對于各類軌道梁都有力學性能及動力性能方面的研究，而對于關節型五開道岔梁的研究則較少，并且特別缺乏關于此類道岔梁動力特性及疲勞壽命方面的研究。

筆者使用ANSYS Workbench軟件對道岔梁的3號梁進行結構靜強度分析和模態分析，得到道岔梁的應力分布云圖、模態頻率及振型，從強度分析和模態分析上校核該結構的合理性，最后對道岔梁進行疲勞壽命預測，為后續的優化設計提供數據支持。

1 道岔梁

1.1 道岔梁結構

圖1為道岔梁5個梁段的連接示意。1、3、5號梁段的結構相同，2、4號梁段相同。筆者以3號道岔梁為研究對象，該梁長6 m，寬1.43 m，高1.42 m。梁的主體全部使用Q235材料，由204塊鋼板焊接而成，屬于箱體結構，內部由8段隔板支撐，如圖2。

圖1 道岔梁連接示意

圖2 3號梁段模型

1.2 加載情況

由于輕軌列車單節車廂長13.9 m，由4組軸承支撐，軸間距分別為1 500，8 100，1 500 mm，而相鄰兩節車廂的軸間距是3 100 mm，如圖3。故3號道岔梁承受最大列車載荷時，有3個車軸作用在梁上，但計算其產生的載荷彎矩及支點反力小于2個車軸產生的彎矩，考慮到加載的方便，還是采用2個車軸標準荷載進行計算，只是將安全系數增加為1.5倍。

以3號道岔梁支座為起點，在左側1.55 m和3.05 m處分別設置2個加載點，作為輕軌列車作用于3號道岔梁的加載位置，如圖4。

圖4 道岔梁豎向加載位置

1.3 3號梁加載情況

道岔梁的工作荷載分為：①主要工作荷載，包括道岔梁的自重、列車豎向靜力荷載、列車豎向動力作用、列車橫向荷載或離心力(取其中較大值)；②附加荷載，包括風荷載、列車制動力及牽引力、溫度影響力、船只或汽車撞擊力、雪荷載、地震力等。筆者只考慮風荷載和列車制動力及牽引力。3號道岔梁受力如圖5，加載情況如圖6。

圖5 道岔梁受力

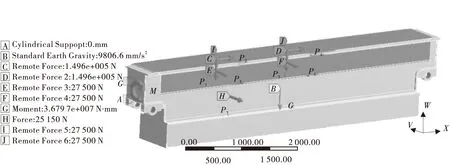
圖6 模型加載

1.4 3號梁荷載計算

計算采用的相關參數如下：

1)道岔梁自重5.58 t，即：G=55.80 kN。

2)列車單軸豎向標準荷載F1=110 kN，列車豎向動力作用F2=F1×μ=39.60 kN，列車單軸豎向標準荷載與列車豎向動力作用的合力即是豎向荷載P1=P3=149.60 kN。

3)制動力按單軸豎向標準荷載的25%計算，即P5=P1×25%=27.50 kN。

4)列車橫向載荷(橫向載荷以列車單軸豎向標準載荷的25%計)P5=P6=27.50 kN，經計算橫向載荷大于離心力，故只取橫向載荷做計算。

5)按風速24 m/s，正面風壓pz=1 000 Pa，風載荷分解成兩部分，一部分直接作用在道岔梁的傾面上，另一部分作用在車體上，在梁上可簡化為橫向力P7=25.15 kN與扭轉力矩M=36.80 kN·m。各荷載明細如表1。

表1 荷載及加載位置

2 有限元建模

2.1 網格劃分

考慮到道岔梁3號梁(以下簡稱“道岔梁”)受力狀況復雜，在有限元建模時采用四面體10節點的Solid187實體單元進行網格劃分。本模型設定最小網格單元尺寸為70 mm，一共建立了286 341個節點，148 752個單元，如圖7。

圖7 整體有限元模型

2.2 約束邊界條件

依據道岔梁的實際安裝位置，在道岔梁的左右兩端的T形安裝孔，即圖8中A，B，C，D共4個位置設置約束。采取圓柱面約束，軸向、徑向和切向的平動都固定，沿安裝孔軸線平動方向的自由度不作約束。

圖8 模型約束

2.3 材料參數

道岔梁的主要材料是Q235-B，其軸向許用應力135 MPa，抗彎許用應力140 MPa，抗剪許用應力80 MPa，屈服強度235 MPa，極限強度390 MPa，彈性模量E=2.1×105MPa，剪切模量G=8.1×104MPa，泊松比ν=0.3。

3 研究方案

3.1 靜強度研究方案

依據工作荷載的性質，將含有全部主要工作荷載的工況劃定為方案1，可以了解一般情況下的道岔梁工作狀態；方案2、方案3考慮到附加荷載中的風荷載和制動力對道岔梁的影響，可以對極端情況下的工作狀況進行分析。3個方案工作荷載依次增多，符合道岔梁的3類工作狀況，見表2。

表2 方案明細

3.2 模態研究方案

自由模態分析不考慮任何約束的影響，得到的是結構本身的固有特性。在不同的約束狀態下，結構的固有頻率和振型往往會發生改變，在約束狀態下對結構體的模態分析稱之為約束模態分析。相對于自由模態分析，約束模態分析更加符合實際情況。因此筆者對道岔梁進行約束模態分析，可以判斷道岔梁對各類型的動力荷載是如何響應的。

3.3 疲勞分析方案

采用ANSYS Workbench疲勞分析模塊，立足現有條件選取合適的載荷譜與P-S-N曲線后，利用線性累積損傷理論對道岔梁進行應力疲勞分析，計算其疲勞壽命。

3.3.1 疲勞性能參數

根據《機械工程材料性能數據手冊》[7]，查取Q235-B鋼圓柱型缺口試樣的P-S-N曲線，如圖9。

圖9 Q235-B級鋼圓柱型缺口試樣P-S-N曲線

選取置信度為99.9%的S-N曲線，將對應的應力值與循環次數輸入到有限元模型的材料屬性庫中，作為道岔梁的疲勞屬性參數。

3.3.2 載荷譜

采用ANSYS軟件自帶的變幅值隨機載荷作為疲勞分析的輸入載荷。該載荷譜是類似于白噪聲的隨機信號，調整幅值使其接近靜強度分析的最大應力值后可作為疲勞載荷譜使用。載荷譜如圖10。

圖10 隨機載荷譜

靜強度分析的最大應力值在乘以安全系數后約為65.55 MPa，考慮到工作載荷在實際中會出現耦合現象，即應力幅值有增大的可能，因此比例系數調整至0.003 5，將載荷譜的應力值范圍限定在0～143.91 MPa這樣一個較大的區域，平均應力值范圍在-164.92～122.9 MPa。

由于載荷譜并不是R=-1的對稱循環載荷，而是應力比不定，平均應力不為0的變幅值載荷，因此有必要選擇合適的平均應力修正理論來對S-N曲線進行修正。考慮到古德曼理論主要用于塑性很低的脆性材料，如鑄鐵、高強度鋼等，適合Q235-B鋼的材料特性，且該理論便于計算，因此選用古德曼理論作為平均應力修正理論。

4 結果分析

4.1 靜強度分析

方案1、方案2、方案3的等效應力最大值分別為48.20，49.45，52.44 MPa，其等效應力云圖如圖11。

圖11 等效應力云圖

從圖11中可以看出，道岔梁應力主要分布在梁的中下部，符合列車運行時道岔梁承受列車壓力的狀況。隨著工作載荷的增多，等效應力值隨之增大。考慮到安全系數后，最大等效應力值是65.55 MPa，小于材料屈服應力235 MPa，也小于軸向允許應力135 MP。

3種方案最大等效應力都在道岔梁端部的側板與其它板面焊接處，屬于應力集中點，如圖12。

圖12 等效應力最大點

4.2 剛度分析

從圖13可看出，道岔梁變形很不均勻，但豎向(y向)最大變形只有0.29 mm，發生在梁的中上部；橫向(x向)最大變形是0.26 mm，發生在梁的中部。根據GB 50017—2003《鋼結構設計規范》[8]，橋跨結構在列車靜活載作用下，豎向撓度不應超過L/800，橫向撓度不應超過L/4 000(L為梁的跨度，單位：m)。道岔梁最大豎向位移為0.29mm，小于許用值6 000/800=7.5 mm；橫向位移為0.26 mm，小于許用值6 000/4 000=1.5 mm。因此，道岔梁剛度滿足要求，且有較大裕量。

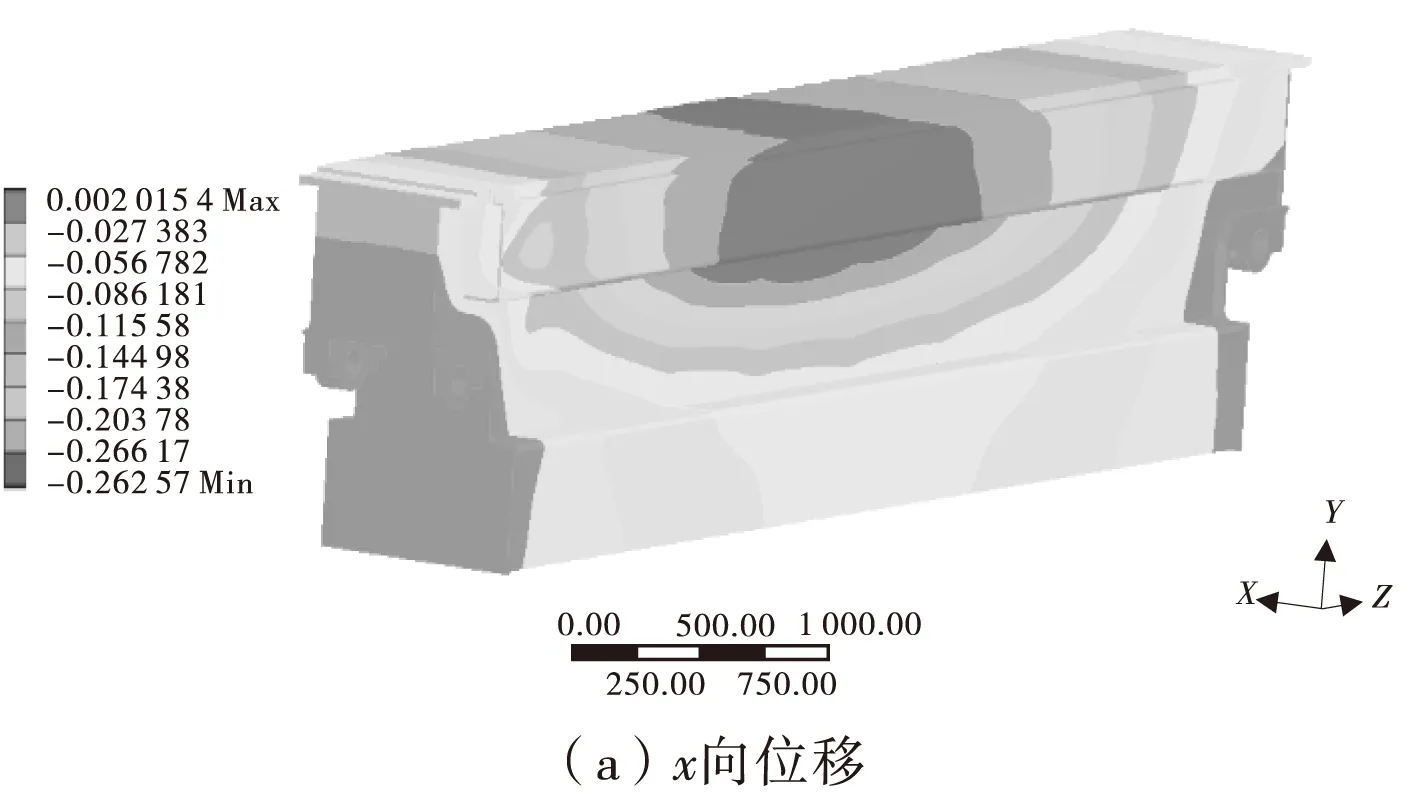
圖13 位移

有限元分析結果說明，道岔梁有應力集中點是該結構的薄弱處，需要在結構設計或者焊接加工中加以改進，以避免出現應力集中[9]。另外道岔梁等效應力遠低于材料的屈服強度，可以考慮在設計上進行結構優化，減輕質量以提高道岔梁的經濟性[10]。

4.3 模態分析

前4階約束模態固有頻率及振型如圖14。

圖14 第1～4階振型

可看出道岔梁的固有頻率隨著振型階次逐漸增大，前3階振型的變形最大點都在梁的中上部，可以考慮加大該處的剛度，降低局部振幅。由于軌道梁橋跨結構的橫向自振頻率應不小于70/L(跨度L=6 m)[8]，因此道岔梁橫向自振頻率的下限為：70/6=11.7 Hz。對比表3中的各階次頻率，可看出道岔梁橫向剛度足夠，道岔梁對外部載荷的動態響應不靈敏，基本可忽略。

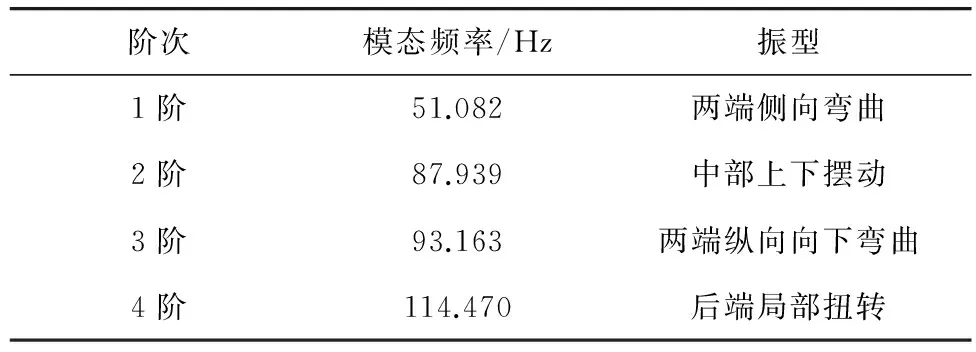
表3 各階次固有頻率

4.4 疲勞壽命分析

圖15中矩形塊的高低反映了它們表示的應力循環次數的多少，矩形越高則循環次數越大。從圖中可看出低于100 MPa的載荷值占絕大多數，應力幅值在60 MPa以上的循環次數約75次，應力循環總次數約900次。

圖15 雨流陣列

圖15反映的雨流計數結果是對整個隨機載荷譜進行的計數結果，然而這個載荷譜是道岔梁多個工作周期(完成一次道岔為一個工作周期)的總和，它包含了道岔梁若干個工作周期(周期數以T表示)。仿真計算得到的疲勞循環次數以N表示，T與N的乘積即是道岔梁的疲勞壽命(即道岔梁不發生疲勞失效的總道岔次數)，用S表示。

考慮到一輛輕軌列車共有6節車廂，每節車廂有2個車軸，可得出列車經過道岔梁時有12次最大應力加載。雨流計數結果顯示，應力幅值在60 MPa以上的循環次數達到75次，兩數相除即得T=6。

道岔梁的疲勞壽命等值線圖如圖16。可以看出道岔梁最危險部位可以承受3.259×105次循環加載，道岔梁的疲勞壽命S：

S=T×N=6×3.259×105=1.955×106

按道岔梁每10 min 工作1次，1天工作18 h計，道岔梁疲勞壽命年數為：

滿足《鋼結構設計規范》中對鋼結構25a的最低壽命設計要求。

圖16 疲勞壽命等值線

5 結 論

1)靜強度分析結果得出最大等效應力值σmax=52.44 MPa，為Q235-B材料屈服強度的22.3%。說明3號道岔梁在靜強度上安全，但是局部位置存在明顯的應力集中現象，需要通過改進設計或制造工藝消除該現象。

2)道岔梁變形最大點在梁的中上部，需要考慮增強局部剛度。約束模態分析結果顯示，該鋼結構固有頻率值隨著外部載荷的施加變化不大，1階振型的固有頻率約51 Hz，動態響應不明顯。道岔梁疲勞壽命仿真結果是49.6 a，符合鋼結構25 a的壽命設計要求。

3)運用ANSYS有限元軟件對道岔梁進行靜力分析和模態分析，能夠較好的反映出道岔梁的應力變形情況和振動情況，總體來說該結構是安全的。

[1] GB 50458—2008 跨座式單軌交通設計規范[S].北京:中國建筑工業出版社,2008. GB 50458—2008 Code for Design of Straddle Monorail Transit[S].Beijing:China Architecture & Building Press,2008.

[2] 楊佑發,王立福.跨座式單軌交通箱形鋼軌道梁動力特性研究[J].橋梁建設,2004(2):12-14. Yang Youfa,Wang Lifu.Study of dynamic behavior of steel box rail beam for straddle type monorail transit[J].Bridge Construction,2004(2):12-14.

[3] 時瑾.不同型式磁浮軌道梁動力響應分析[J].中國科技論文在線,2012,7(11):841-845. Shi Jin.Dynamic response of different guide way structures of maglev[J].Sciencepaper Online,2012,7(11):841-845.

[4] 牛均寬.跨座式關節型道岔梁靜力分析及制造工藝性研究[J].橋梁,2006(10):60-63. Niu Junkuan.Static analysis and manufacturing study of the straddle type joint turnouts beam[J].Bridge,2013(10):60-63.

[5] 李振華.跨座式單軌交通平移式道岔靜、動力學分析[D].北京:北京交通大學,2010. Li Zhenhua.Static & Dynamic Analysis of Translational Switch in Straddle-Monorail[D].Beijing:Beijing Jiaotong University,2010.

[6] 顧行濤.高速磁浮車輛-道岔梁耦合振動建模與仿真分析[D].成都:西南交通大學,2009. Gu Xingtao.Modeling and Simulation of Coupling Vibration Between High-Speed Maglev Vehicle and Switch Beam[D].Chengdu:Southwest Jiaotong University,2009.

[7] 方向威,吳明達.機械工程材料性能數據手冊[M].北京:機械工業出版社,1994. Fang Xiangwei,Wu Mingda.Handbook for Performance Data of Mechanical Engineering Materials[M].Beijing:China Machine Press,1994.

[8] GB 50017—2003 鋼結構設計規范[S].北京:中國標準出版社,2003. GB 50017—2003 Code for Design of Steel Structures[S].Beijing:Standards Press of China,2003.

[9] 易晉生,顧安邦,王小松.車橋耦合振動理論在橋面不平度研究中的應用[J].重慶交通大學學報：自然科學版,2013,32(4):560-563. Yi Jinsheng,Gu Anbang,Wang Xiaosong.Application of vehicle-bridge coupling vibrations theory in the study of bridge surface roughness[J].Journal of Chongqing Jiaotong University:Natural Science,2013,32(4):560-563.

[10] 周水興,滿澤聯,周光強,等.連續剛構橋組合式橋墩臨界荷載分析[J].重慶交通大學學報:自然科學版,2014,33(1):17-20. Zhou Shuixing,Man Zelian,Zhou Guangqing,et al.Critical load of combined pier for continuous rigid frame bridge[J].Journal of Chongqing Jiaotong University:Natural Science,2014,33(1):17-20.

Static, Dynamic and Fatigue Life Analysis of Straddle Type Joint Turnouts Beam

Wang Zhixiang1,2, Zhu Ming1, Zhang Jixiang1,2

(1.College of Mechatronics & Automobile Engineering, Chongqing Jiaotong University, Chongqing 400074, China; 2. Chongqing City Special Ship Digital Design & Manufacturing Engineering Technology Research Center, Chongqing Jiaotong University, Chongqing 400074, China)

The static, modal and fatigue life analysis of the third segment of joint five-switch beam has been studied by the ANSYS Workbench. The analysis displayed that the maximum equivalent stress under static loads is 52.44MPa, less than the yield limit strength of the material. Maximum deformation is about 0.29mm in the upper beam. There is obvious stress concentration point occurred in the welding position. Frequency of the first modal is about 51Hz. The simulation result of switch beam’s fatigue life is 49.6 years. The results of analysis show that the static strength of the switch beam meets requirements. The deformation position of the first three modes in modal analysis coincides with the static strength deformation. The rigidity of this position needs to be strengthened. The fatigue life of switch beam satisfies the requirement of 25 years life of steel structure.

bridge engineering; switch beam; modal analysis; strength

10.3969/j.issn.1674-0696.2015.01.01

2014-01-16；

2014-07-07

王智祥(1955—)，男，四川資陽人，教授，主要從事先進制造技術與應用、船舶數字化設計與制造方面的研究。E-mail：wzx@cqjtu.edu.cn。

張繼祥(1971—)，男，山東菏澤人，副教授，博士，主要從事塑料成型技術及模具設計方面的研究。E-mail：Jixiangzhang@163.com。

U441+.4

A

1674-0696(2015)01-001-05