拱腳轉(zhuǎn)動對圓拱穩(wěn)定性的影響研究

鄧一三，徐 斌，王燕楠

(1. 中國中鐵西南科學研究院，四川 成都 610031；2.西南石油大學 機電工程學院，四川 成都 610500)

?

拱腳轉(zhuǎn)動對圓拱穩(wěn)定性的影響研究

鄧一三1，徐 斌1，王燕楠2

(1. 中國中鐵西南科學研究院，四川 成都 610031；2.西南石油大學 機電工程學院，四川 成都 610500)

根據(jù)能量法，建立基于拱腳轉(zhuǎn)動的平衡方程和平衡穩(wěn)定性方程，分析了拱腳轉(zhuǎn)動對兩端固支圓拱屈曲性能的影響。研究表明：拱腳轉(zhuǎn)動將導(dǎo)致拱的極限屈曲荷載減小，越是深拱，其影響越明顯；拱的長細比越小，拱腳轉(zhuǎn)動對極限屈曲荷載的影響越明顯；拱腳轉(zhuǎn)動將改變拱屈曲方式的拱型幾何參數(shù)分界值，反對稱的平衡分岔屈曲的范圍將隨著拱腳轉(zhuǎn)動的增加而擴大。

橋梁工程；拱腳轉(zhuǎn)動；屈曲荷載；屈曲方式；能量法

拱結(jié)構(gòu)以其優(yōu)美的結(jié)構(gòu)造型、簡潔的傳力路徑和經(jīng)濟的造價被廣泛應(yīng)用于橋梁與建筑結(jié)構(gòu)，其穩(wěn)定性問題的研究也一直備受關(guān)注。

1962年，A．Gjelsvik，等[1]首次應(yīng)用能量法研究了集中荷載下變截面固支拱的屈曲問題；隨后H．L．Schreger，等[2]對固支矩形截面拱的對稱屈曲進行了分析；J．F．Dickie，等[3]研究了鉸支和固支矩形截面淺圓拱的屈曲問題；Pi Yonglin，等[4]研究了支承剛度和沖擊荷載對臨界荷載以及屈曲方式的影響；M．Jiho，等[5]研究了拋物線鉸支拱的非線性屈曲性能。近年來，國內(nèi)學者也對拱的屈曲穩(wěn)定性問題進行了大量的研究[6]。劇錦三，等[7]研究了拱結(jié)構(gòu)的彈性二次屈曲性能；戴莉莉，等[8]和李召兵，等[9]在拱的屈曲分析中引入突變理論；陳浩軍，等[10]用有限元法研究了拱結(jié)構(gòu)屈曲的幾何非線性特性；程鵬，等[11]完整的考慮了橫向應(yīng)力和剪應(yīng)力的二階效應(yīng)，推導(dǎo)了拱的非線性平衡方程；衛(wèi)星，等[12]在拱的面內(nèi)彈性屈曲中考慮了二階效應(yīng)。

隨著現(xiàn)役拱橋和拱結(jié)構(gòu)建筑建造年齡的增長，往往因局部地基承載力不足導(dǎo)致拱腳擾動，從而對拱結(jié)構(gòu)的承載能力及穩(wěn)定性產(chǎn)生不利的影響。筆者以兩端固支圓拱為對象，研究在不同的拱的長細比和深坦度下，拱腳轉(zhuǎn)動對拱結(jié)構(gòu)承載能力和穩(wěn)定性的影響。

1 拱腳轉(zhuǎn)動引起的彎曲和膜應(yīng)變

當拱腳支承處發(fā)生轉(zhuǎn)動時，將引起超靜定固支拱內(nèi)的附加內(nèi)力。根據(jù)彈性中心法，拱腳左端發(fā)生逆時針轉(zhuǎn)腳位移時，拱圈內(nèi)的彎曲應(yīng)變εb和膜應(yīng)變分εm為：

(1)

(2)

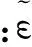
式中：rx為截面的慣性半徑；f為拱高；ys為彈性中心到拱頂?shù)木嚯x；R為拱半徑；L為拱跨；Θ為拱張開角的1/2。

拱的幾何形狀見圖1。

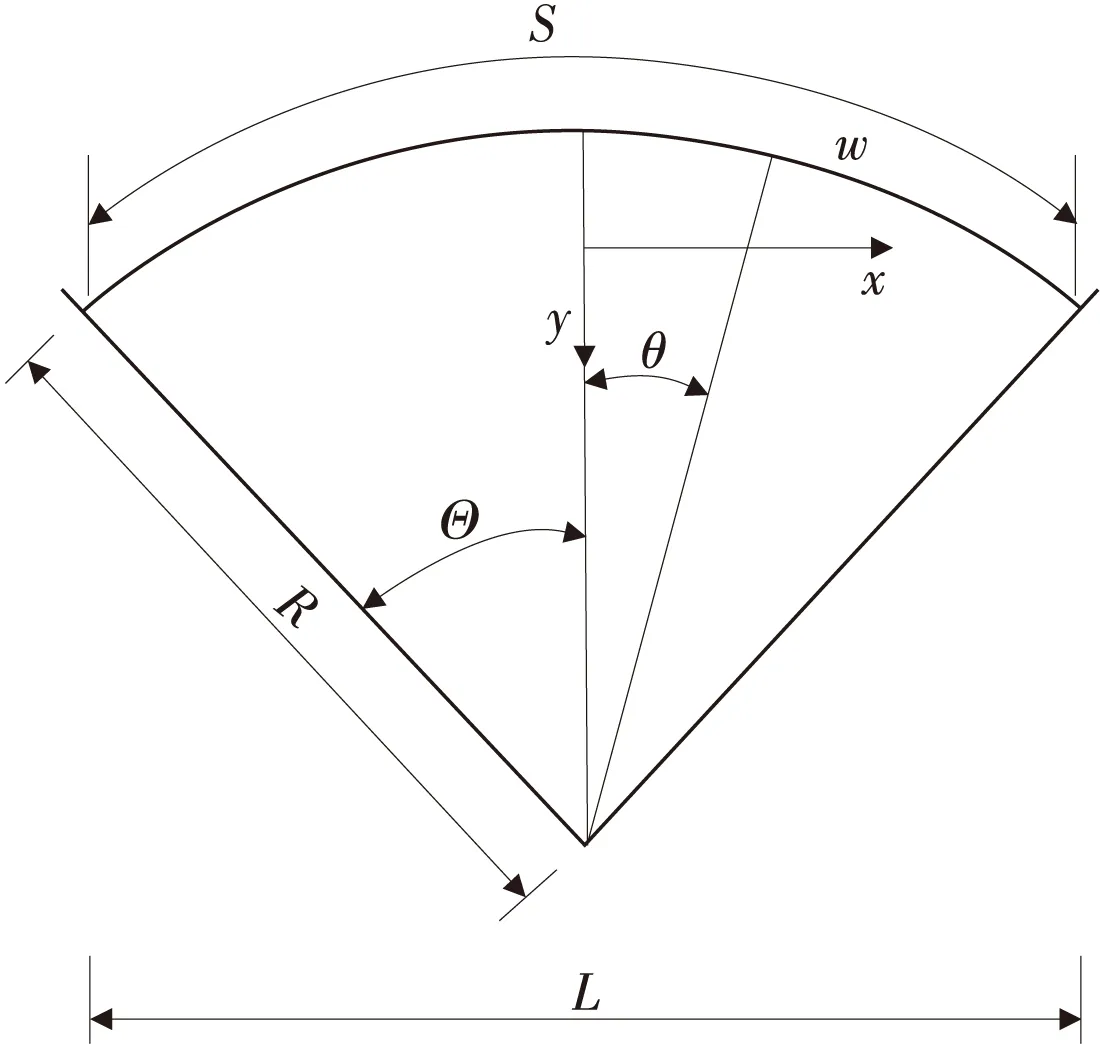
圖1 拱的幾何形狀和坐標

2 基于拱腳轉(zhuǎn)動的屈曲臨界平衡穩(wěn)定方程

根據(jù)結(jié)構(gòu)總勢能定義，并將總勢能表達式除以常量E·A·R，得到修正的結(jié)構(gòu)總勢能：

(3)

根據(jù)結(jié)構(gòu)穩(wěn)定性的能量準則，總勢能的一階變分為0時結(jié)構(gòu)處于平衡臨界狀態(tài)，可得到徑向和軸向的平衡方程分別為：

n3)=0

(4)

(5)

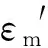
式中：μ2=NR2/(EI)；N是常數(shù)，為膜應(yīng)力的合力。

根據(jù)膜應(yīng)變等于拱結(jié)構(gòu)的平均軸向應(yīng)變，可建立補充方程：

(6)

聯(lián)立平衡方程式(4)、式(5)和補充方程式(6)，并代入兩端固支圓拱的邊界條件，可得考慮拱腳轉(zhuǎn)動的臨界平衡方程：

(7)

式中：H′和G′均是關(guān)于μ，α，Θ，S，和λs的函數(shù)；S為拱軸線長度；λs=0.25(S/rx)(S/R)為拱型幾何參數(shù)，S/rx反映了拱的長細比，S/R反映了拱的深坦度；β=(Ncr-N)/N；Ncr=qcrR為平衡臨界狀態(tài)下考慮拱腳轉(zhuǎn)動的組合名義軸力。

3 基于拱腳轉(zhuǎn)動屈曲平衡穩(wěn)定性分析

總勢能的2階變分為0，顯示了結(jié)構(gòu)平衡從穩(wěn)定狀態(tài)到不穩(wěn)定狀態(tài)的過渡，為屈曲發(fā)生的標志。總勢能式(3)的二階變分為：

(8)

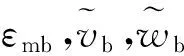
令δ2Π*=0，可得到徑向和軸向的平衡穩(wěn)定方程分別為：

(9)

根據(jù)膜應(yīng)變等于拱結(jié)構(gòu)的平均軸向應(yīng)變，可建立補充方程：

(10)

拱的面內(nèi)屈曲方式分別為反對稱的分岔屈曲和對稱的極值點屈曲。

3.1 基于拱腳轉(zhuǎn)動的反對稱分岔屈曲平衡穩(wěn)定性

εmb=0

(11)

將平衡穩(wěn)定方程(9)和補充方程(11)聯(lián)立，并代入固支圓拱邊界條件，可得反對稱平衡分岔屈曲下結(jié)構(gòu)平衡穩(wěn)定的臨界條件：

μΘ=1.430 3π

(12)

聯(lián)立式(7)與式(12)，即可求出未知量β和μ，從而得到反對稱平衡分岔屈曲時臨界狀態(tài)下的Ncr值，最終求得反對稱平衡分岔屈曲的臨界荷載qcr。

3.2 基于拱腳轉(zhuǎn)動的對稱極值點屈曲平衡穩(wěn)定性

C1·β2+C2·β+C3=0

(13)

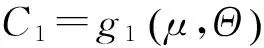
式(13)也是關(guān)于未知量β和μ，并與拱腳轉(zhuǎn)角位移α和拱型參數(shù)λs有關(guān)的方程。同理可通過聯(lián)立式(7)與式(13)，求得對稱極值點屈曲的臨界荷載qcr。

4 拱腳轉(zhuǎn)動對屈曲性能影響分析

拱腳轉(zhuǎn)動對屈曲性能的影響主要體現(xiàn)在對拱的極限屈曲荷載大小、屈曲方式的影響，以及產(chǎn)生拱腳轉(zhuǎn)動時，長細比和深坦度對拱屈曲性能影響的變化。

筆者研究了徑向均布荷載作用下，兩端固支圓拱在拱腳左端發(fā)生逆時針的轉(zhuǎn)角位移時，不同參數(shù)下拱腳轉(zhuǎn)動對拱的屈曲性能的影響(拱體的彈性模量E=3.3e11 Pa，截面慣性矩I=0.046 875 m4，截面高H=0.866 m，截面面積A= 0.75 m2)。

圖2描述了拱的長細比S/rx=100時(S/rx一定，λs反映了拱的深坦度)，不同的深坦度下(λs分別為52.36，31.42，22.44和13.09)Ncr/NFB值隨拱腳逆時針轉(zhuǎn)角α的變化規(guī)律。

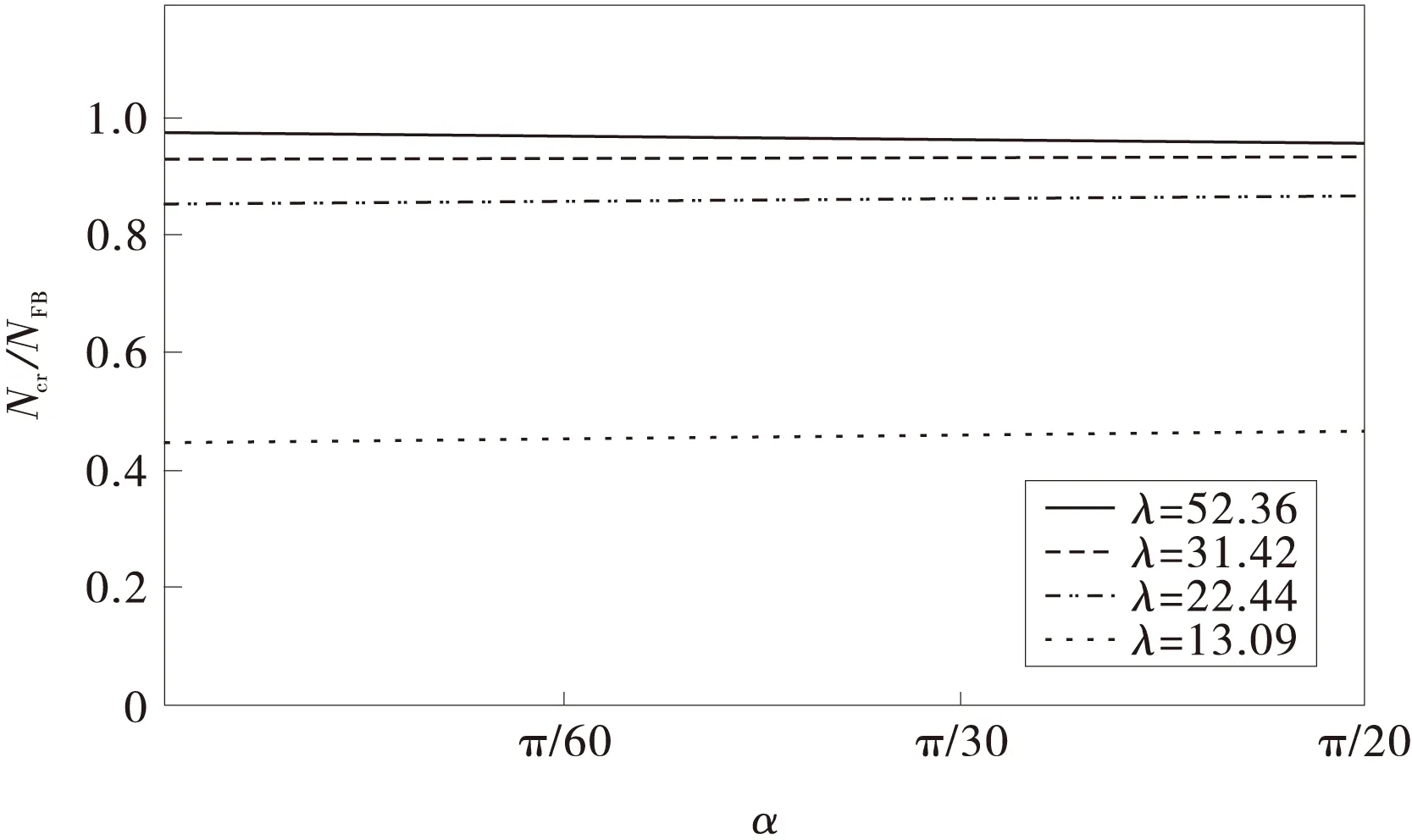
圖2 拱腳轉(zhuǎn)動的α-Ncr/NFB圖

圖2中：NFB=(1.430 3π)2EI/(S/2)2為無拱腳轉(zhuǎn)動的臨界軸力[14]。可見：越是深拱，Ncr/NFB值越明顯的隨著拱腳轉(zhuǎn)角α的增大而減小；而拱越坦，則影響越不明顯。表明當拱的長細比一定時，不同深坦度下，拱腳的逆時針轉(zhuǎn)角位移對極限屈曲荷載的影響不同。

圖3描述了拱的長細比S/rx=100時，在不同的拱腳轉(zhuǎn)動下(α分別為0，π/40和π/20)Ncr/NFB值隨λs的變化。可見：①當拱腳轉(zhuǎn)角α一定時，隨著λs值的減小，拱的屈曲方式逐漸從反對稱的平衡分岔屈曲變?yōu)閷ΨQ的極值點屈曲；②當拱腳左端產(chǎn)生α=π/40和α=π/20的逆時針轉(zhuǎn)角位移時，屈曲方式的拱型幾何參數(shù)分界值由無拱腳轉(zhuǎn)動時的λs≈17.5分別變?yōu)棣藄≈17.1和λs≈16.8，表明逆時針拱腳轉(zhuǎn)動擴大了拱反對稱分岔屈曲的范圍。

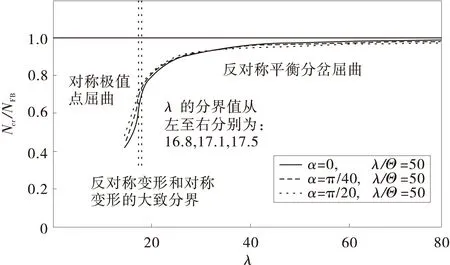
圖3 拱腳轉(zhuǎn)動的λs-Ncr/NFB圖

圖4描述了拱腳轉(zhuǎn)動一定時(α=π/20)，不同的長細比下(λs/Θ分別為25，50，75和100)，Ncr/NFB值隨拱的深坦度Θ的變化。可見：當拱的深坦度一定時，拱腳轉(zhuǎn)動對極限屈曲荷載的影響隨著長細比的增加而減小。即當拱的長細比較小時，拱腳轉(zhuǎn)動對極限屈曲荷載的影響較大，反之則較小。

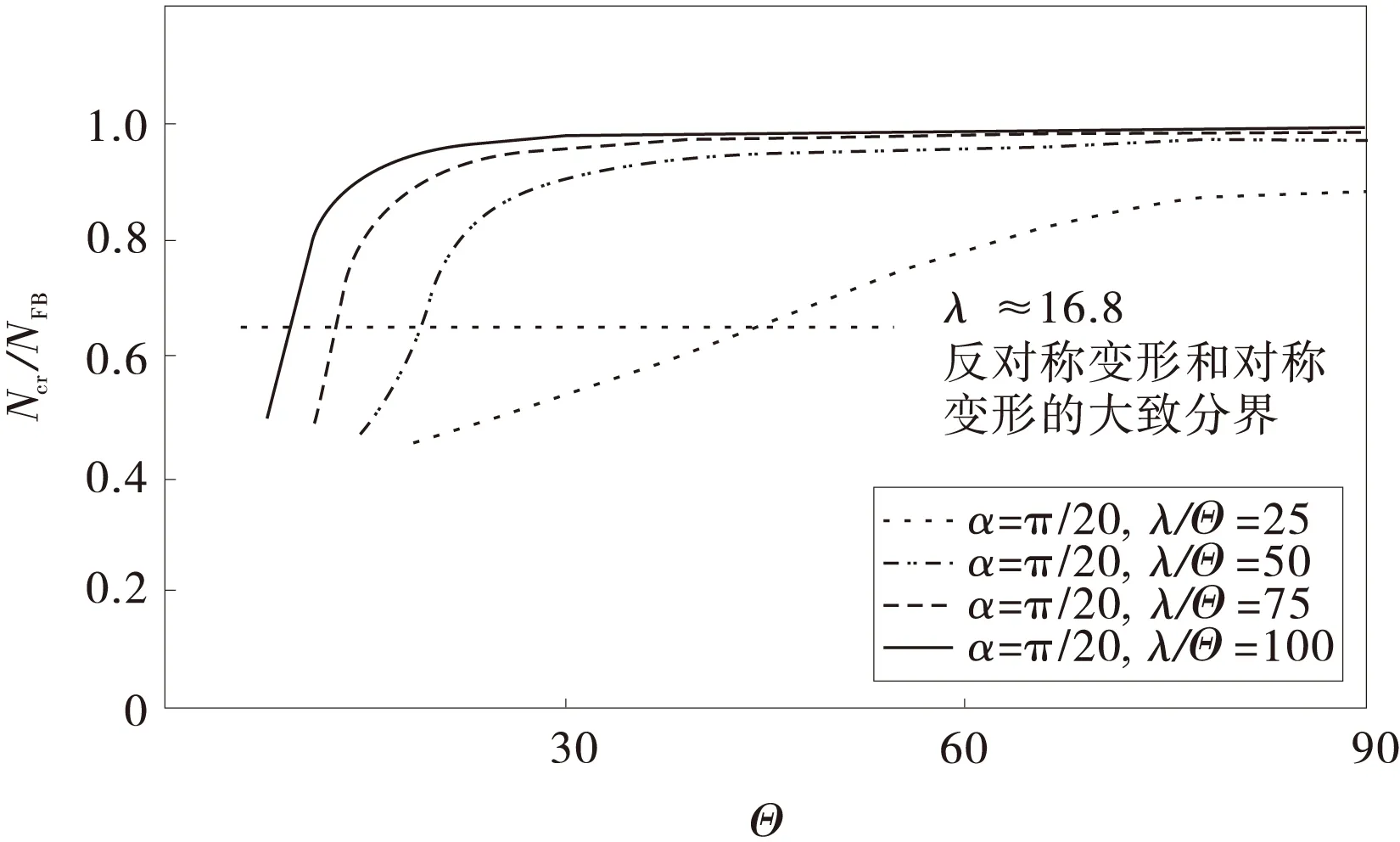
圖4 拱腳轉(zhuǎn)動的Θ-Ncr/NFB圖

5 結(jié) 語

以固支圓拱為研究對象，通過能量法建立了基于拱腳轉(zhuǎn)動的平衡方程和平衡穩(wěn)定性方程，分析了拱腳轉(zhuǎn)動對拱屈曲性能的影響。研究表明：拱腳轉(zhuǎn)動將導(dǎo)致拱的極限屈曲荷載減小，越是深拱，其影響越明顯；拱的長細比越小，拱腳轉(zhuǎn)動對極限屈曲荷載的影響越明顯；拱腳轉(zhuǎn)動將改變拱屈曲方式的拱型幾何參數(shù)分界值，反對稱的平衡分岔屈曲的范圍將隨著拱腳轉(zhuǎn)動的增加而擴大。

[1] Gjelsvik A,Bodner S R.Energy criterion and snap-though buckling of arches [J].Journal of the Engineering Mechanics Division,1962,88(5): 87-134.

[2] Schreyer H L,Masur E F.Buckling of shallow arches [J].Journal of the Engineering Mechanics Division,1966,92(4): 1-17.

[3] Dickie J F,Broughton P.Stability criteria for shallow arches [J].Journal of the Engineering Mechanics Division,1971,97(3): 951-965.

[4] Pi Yonglin,Trahair N S.Non-linear buckling and post buckling of elastic arches [J].Engineering Structures,1998,20(7): 571-579.

[5] Jiho M,Ki-Yong Yoon,Tae-Hyung Lee.In-plane elastic buckling of pin-end shallow parabolic aches [J].Engineering Structures,2007,29(10): 2611-2617.

[6] 曾德榮,李杰.基于滑移理論的大跨徑鋼管混凝土拱橋穩(wěn)定性分析[J].重慶交通大學學報: 自然科學版,2010,29(3): 344-347. Zeng Derong,Li Jie.Stability analysis on large span concrete-filled steel tube arch bridge based on slip theory [J].Journal of Chongqing Jiaotong University: Natural Science,2010,29(3): 344-347.

[7] 劇錦三,郭彥林,劉玉擎.拱結(jié)構(gòu)的彈性二次屈曲性能[J].工程力學,2002,19(4):109-112. Ju Jinsan,Guo Yanlin,Liu Yuqing.The secondary buckling behavior of elastic arch [J].Engineering Mechanics,2002,19(4): 109-112.

[8] 戴莉莉,魏德敏.彈性拱靜力屈曲的突變行為[J].力學與實踐,2003,25(4):41-43. Dai Lili,Wei Demin.Catastrophic behavior for static buckling of elastic arches [J].Mechanics in Engineering,2003,25(4): 41-43.

[9] 李召兵,陳曉紅.基于突變理論的扁拱跳躍屈曲分析[J].山西建筑,2005,31(14):51-52. Li Zhaobing,Chen Xiaohong.Snap-through buckling analysis of shallow arches based on catastrophe theory [J].Shanxi Architecture,2005,31(14): 51-52.

[10] 陳浩軍,汪優(yōu),黃靚.拱結(jié)構(gòu)屈曲的幾何非線性有限元分析[J].廣東工業(yè)大學學報,2004,21(4):47-51. Chen Haojun,Wang You,Huang Liang.Geometric nonlinear analysis of arch structure by finite element method [J].Journal of Guangdong University of Technology 2004,21(4): 47-51.

[11] 程鵬,童根樹.圓弧拱平面內(nèi)彎曲失穩(wěn)一般理論[J].工程力學,2005,22(1):93-101. Cheng Peng,Tong Genshu.A general theory for in-plane nonlinear analysis of circular arches [J].Engineering Mechanics,2005,22(1): 93-101.

[12] 衛(wèi)星,李俊,李小珍,等.考慮二階效應(yīng)的拱結(jié)構(gòu)面內(nèi)彈性屈曲[J].工程力學,2007,24(1):147-152. Wei Xing,Li Jun,Li Xiaozhen,et al.In-plane secondary buckling behavior of elastic arches [J].Engineering Mechanics,2007,24(1): 147-152.

[13] Pi Yonglin,Bradford M A,Tin-Loi F.Nonlinear analysis and buckling of elastically supported circular shallow arches [J].International Journal of Solids and Structures,2007,44(7/8): 2401-2425.

[14] Pi Yonglin,Bradford M A,Uy B.In-plane stability of arches [J].International Journal of Solids and Structures,2002,39(1): 105-125.

Effects of Angular Displacement of Skewback on Stability Performance of Circular Arch

Deng Yisan1, Xu Bin1, Wang Yannan2

(1. China Southwest Research Institute of China Railway Engineering Co. Ltd., Chengdu 610031, Sichuan, China; 2. School of Mechatronic Engineering, Southwest Petroleum University, Chengdu 610500, Sichuan, China)

According to the energy criterion of structure stability, the balance equation and the equilibrium stability equation were obtained. Next, the effects of angular displacement of skewback on buckling performance of circular arch were worked out by means of the simultaneous solution of balance equation and equilibrium stability equation. The following conclusions can be drawn from the above research: the angular displacement of skewback will lead to the decrease of buckling load of deep arch; the effects of angular displacement of skewback on buckling load are changed by opening angle of arch; the effects of angular displacement of skewback on buckling load are more evident with the decrease of slenderness ratio of arch; the dividing values of geometric parameter of arch are enlarged with the increase of angular displacement of skewback.

bridge engineering; angular displacement of skewback; buckling load; buckling mode; energy method

10.3969/j.issn.1674-0696.2015.01.05

2013-11-20；

2014-02-23

國家自然科學基金項目(51174173)

鄧一三(1982—)，男，四川南充人，工程師，碩士，主要從事結(jié)構(gòu)穩(wěn)定性分析方面的研究。E-mail:dphqbys@163.com。

TU501；TU511.3

A

1674-0696(2015)01-022-03