城市道路交通噪聲的混沌特征及其應用
張文會,羅文文,李 卓,徐慧智
(1. 東北林業大學 交通學院,黑龍江 哈爾濱 150040;2. 北京交通運輸職業學院 汽車工程系,北京 102618)
?
城市道路交通噪聲的混沌特征及其應用
張文會1,羅文文1,李 卓2,徐慧智1
(1. 東北林業大學 交通學院,黑龍江 哈爾濱 150040;2. 北京交通運輸職業學院 汽車工程系,北京 102618)
通過采集城市道路特征斷面的交通噪聲,形成時間序列,采用自相關函數法計算延遲時間,當相關系數衰減為0.4時,計算得到相空間重構的延遲時間為12。利用兩組噪聲樣本的訓練集計算關聯維數,當嵌入維數為6時,關聯維數保持不變,確定系統的嵌入維數為3,從而判定兩組交通噪聲樣本存在混沌特征。根據重構的相空間、狀態點及臨近點計算擬合參數,分別對兩組噪聲樣本進行混沌預測,并與檢驗集比對,結果表明:混沌模型可以用于短時城市道路交通噪聲預測,兩組噪聲樣本的預測平均相對誤差分別為8.56%和9.33%。
交通工程;城市道路;交通噪聲;混沌特征;相空間重構
汽車保有量增加和城市的發展使道路不斷拓寬和延伸,道路格局發生變化,以滿足出行需求。交通噪聲由于其危害性、連續性和遍及性日益受到關注[1],目前關于交通噪聲的研究主要從噪聲輻射和傳播過程中的聲衰減與有關參量的關系[2-3]、噪聲的時間分布和空間分布[4-5]等方面展開。
城市道路交通噪聲是由系統多因素相互耦合作用的綜合反映,如交通流量、交通組成、平均速度和環境等,基于以上多元參數可建立噪聲的預測模型[6-8]。由于交通系統本身是開放、時變的復雜系統,交通噪聲也具有非線性和不確定性,看似隨機的噪聲時間序列,實際包含著混沌運動的基本信息。混沌運動要在三維以上的系統中才能描述,因此要把不規律的交通噪聲時間序列拓展到多維相空間中,以揭示城市道路交通噪聲時間序列的混沌特征。筆者基于相空間重構理論,判別城市道路短時交通噪聲時間序列的混沌特征,并利用混沌模型對檢驗集進行預測。
1 城市道路交通噪聲的采集
交通噪聲的采集地點為城市道路平直路段,距離前后方交叉口500 m以上。采集設備為AWA5610D型積分聲級。為比對采樣時間與混沌特性的關系,采樣時間分別設定為20,40 s,連續記錄噪聲值。其他試驗條件如表1。采集到的噪聲時間序列值如圖1。

表1 交通噪聲采集條件
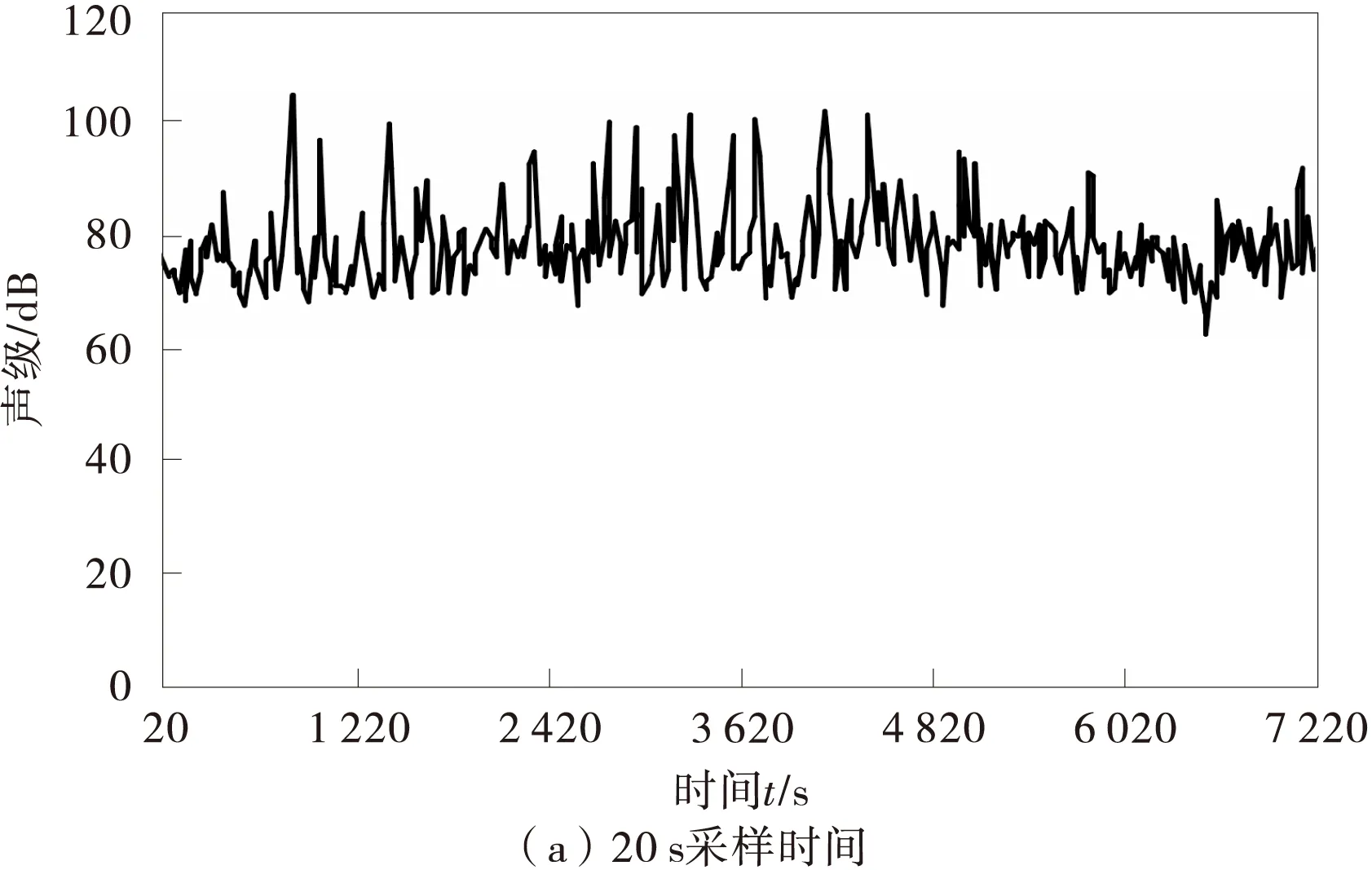

圖1 城市道路交通噪聲時間序列
2 相空間重構理論和延遲時間
一般認為,混沌就是一種低階確定性的非線性動力系統所表現出來的復雜行為。從數學上講,對于確定的初始值,由動力系統就可以推知該系統的長期行為,甚至追溯其過去形態。
2.1 相空間重構理論
相空間重構是根據有限的數據來重構吸引子,以研究系統動力行為的方法。其基本思想是:系統中任一分量的演化都是由與之相互作用的其他分量所決定的,這些分量的信息隱含在任一分量的發展過程中。
設(N,ρ),(N1,ρ1)是兩個度量空間,如果存在映射φ:N→N1滿足:①φ滿射;②ρ(x,y)=ρ1(φ(x),φ(y))(?x,y∈N),則稱(N,ρ),(N1,ρ1)是等距同構的。
如果(N1,ρ1)與另一度量空間(N2,ρ2)的子空間(N0,ρ2)是等距同構的,則稱(N1,ρ1)可以嵌入(N2,ρ2)。
M是d維流形,φ:M→M,φ是一個光滑的微分同胚,y:M→R,y有二階連續導數,φ(φ,y):M→R2d+1,其中:φ(φ,y)=(y(x),y(φ(x)),y(φ2(x)),…,y(φ2d(x))則φ(φ,y)是M到R2d+1的一個嵌入[9]。
上述定理簡而言之就是把具有混沌特性的時間序列重建為一種低階非線性動力學系統,通過相空間重構,可以找出混沌吸引子在隱藏區的演化規律,使現有的數據納入某種可描述的框架之下,從而為時間序列的研究提供一種方法和思路。
設一個m維的動力系統可由式(1)表示:
(1)
通過消元可將式(1)變成一個m階的微分方程:
x(m)=f(x,x(1),…,x(m-1))
(2)
它相當于描述時間演化:
(3)
將其離散化并用差分方程代替各階導數,作適當簡化后有:
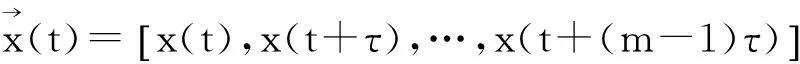
(4)
式中:τ為延遲時間;m為嵌入維數。
式(1)~式(4)即為延滯時間重構的相空間。
2.2 延遲時間的確定
對于無限長的時間序列,可以任意選擇延遲時間τ,但實際時間序列一般是有限長的,因此在相空間重構過程中τ值的選取很重要,筆者采用自相關函數法計算延遲時間,自相關系數定義為:
(5)
一般取自相關系數衰減到一個較小的值時所對應的τ值作為延遲時間,而這個較小值不能選擇太小,否則對應的時間延遲會很大。文獻[10]中給出了一個合理的經驗值為1/e,約為0.4。
根據采集到的交通噪聲時間序列,參照式(5),得到采樣時間分別為20,40 s時自相關系數,如圖2。
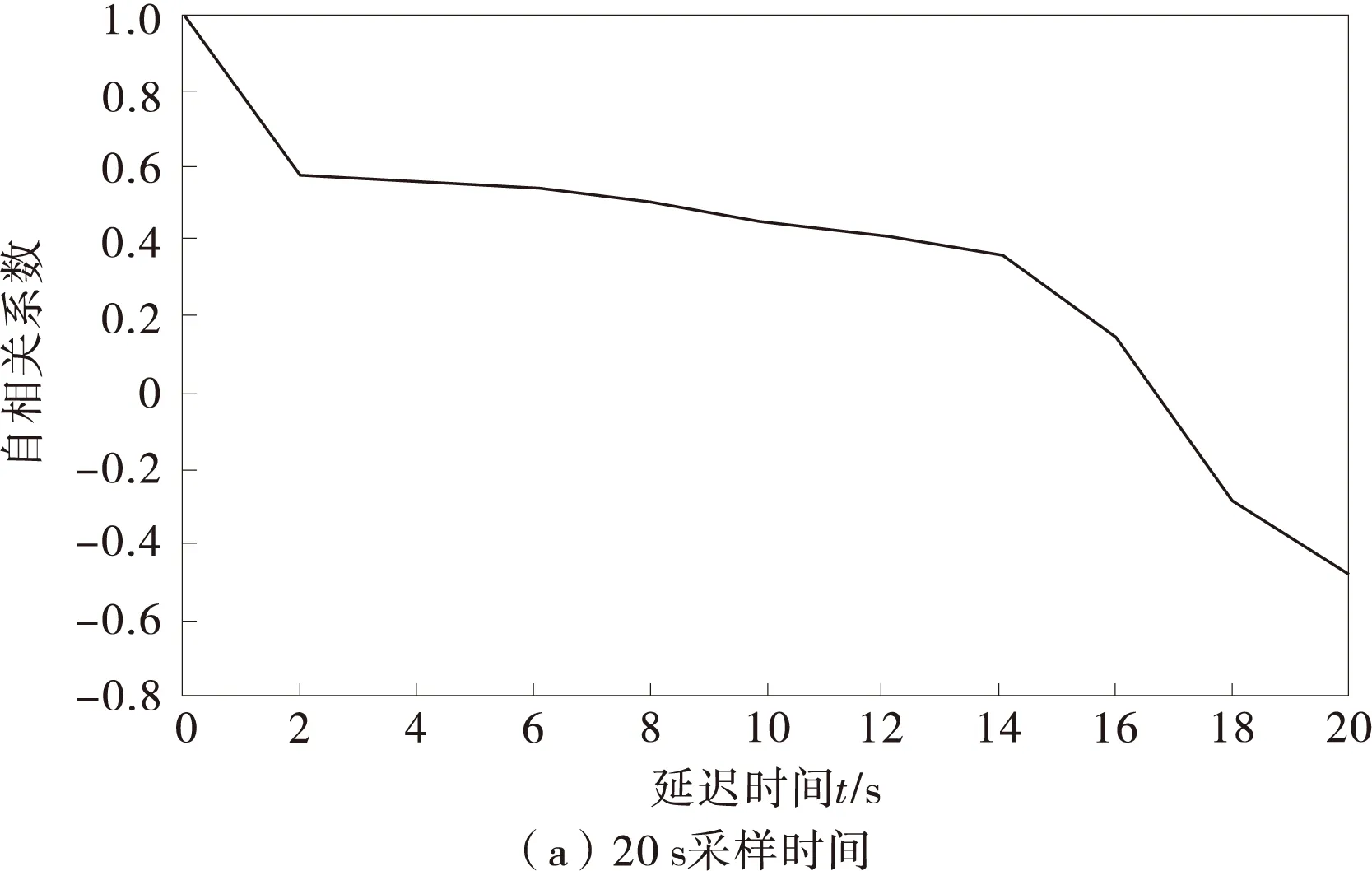
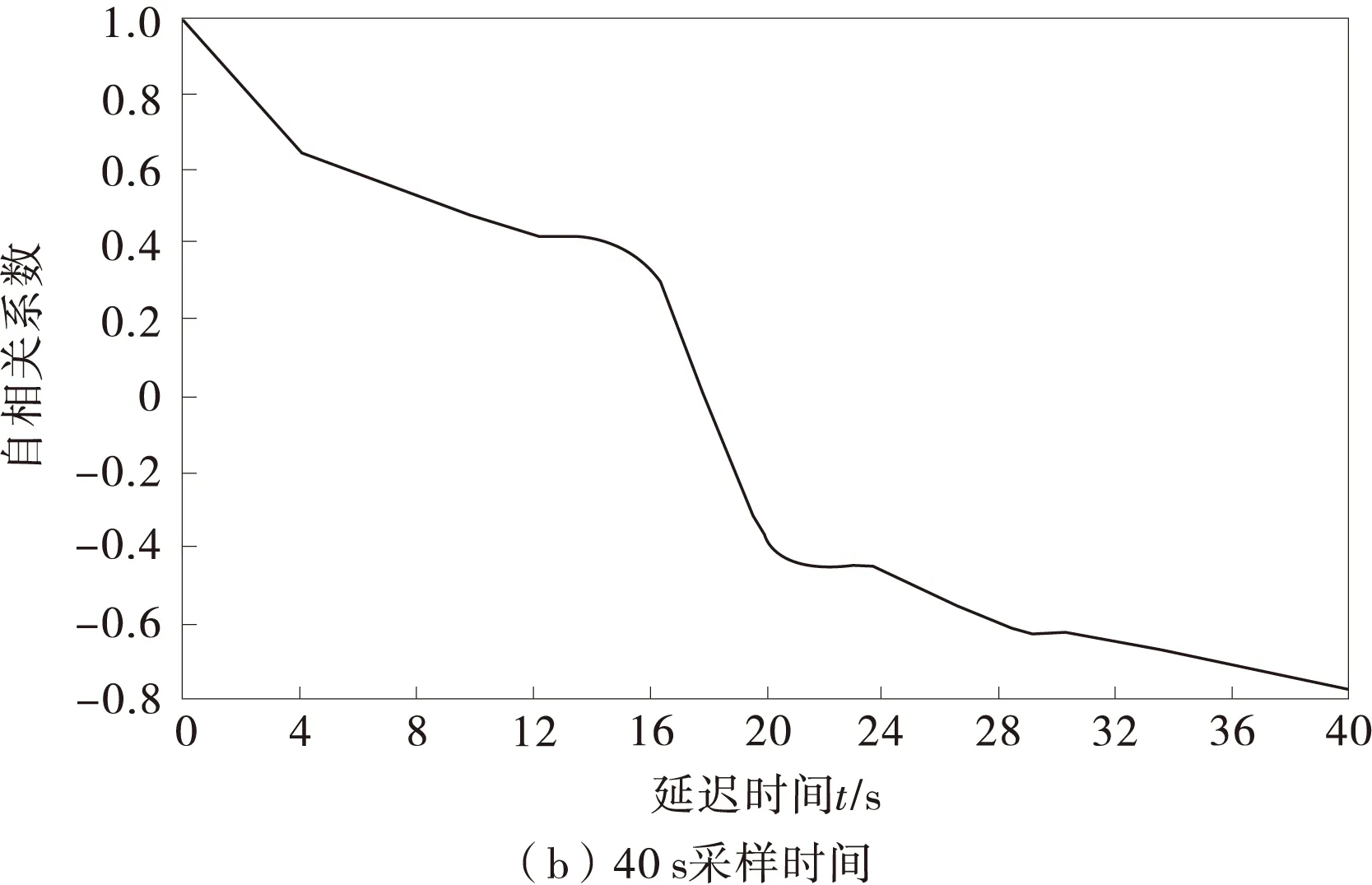
圖2 自相關系數
由圖2可知,當延遲時間為τ=12 s時,自相關系數衰減為0.4左右,因此選擇τ=12 s為重構交通噪聲系統的延遲時間。
3 城市道路交通噪聲的混沌判定
3.1 關聯維數
關聯維數是判別吸引子類型以及復雜程度的表征量,它可以描述系統在整個變化中穩定性和確定性的程度,同時也確定了描述系統所需獨立變量的個數。考察m維(m足夠大) 重構相空間中的兩點:
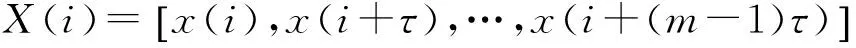
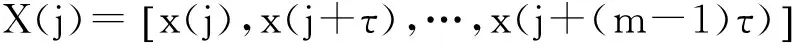
設它們的距離為rij(m),則該距離是一個m維的函數,且有:
(6)
給定一個距離r,并且計算所有距離小于r的相點對數占所有相點對數的比例,記為:
(7)
式中:θ是Heavisible函數,即:
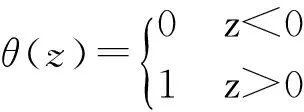
(8)
顯然,C2(r,m)是一個累計函數,它描述了吸引子上兩點距離小于r的概率,表明某點(參照點) 距離小于r的相點的聚集程度,所以稱C2(r,m)為關聯函數。一般r的選取要保證0 (9) 由于式(9)的比例關系與選擇的探測量δ的大小沒有關系,所以可以選擇比例系數為1。 則有: C2(r,m)=(r)D2 (10) 可以求出: (11) 由式(11)可得,D2(m)是嵌入維數的函數,一般稱為關聯維數的估計值。在求解時,一般增加嵌入維數的值,求出不同嵌入維數下關聯維數的估計值,直到估計值不再隨嵌入維數的增大而改變為止,此時的嵌入維數稱為飽和嵌入維數mc。這在lnC2(r,m)-lnr圖中表現為斜率不再發生變化,此時的斜率就是所要求的關聯維數D2=D2(mc)。 如果估計值隨m的增長而增長,并不收斂于一個穩定的值,則表明所考慮的系統是一個隨機時間序列。而關聯維數的存在表明系統具有混沌特性,并為相空間重構中嵌入維數的選擇提供了依據。 3.2 混沌特性的判定 采樣時間為20s(360個噪聲值)時,利用前300個時間序列值作為訓練集來構造初始相空間,余下的60個值(檢驗集)用于檢驗模型精度。將m值由1依次遞增至6,分別獲得lnC2(r,m)與lnr關系圖。限于篇幅,只列出m=6時二者的關系(圖3)。 圖3 lnC2(r,m)與lnr的關系(m=6) 由圖3可知,當嵌入維數為6時,曲線的斜率接近不變,即關聯維數保持為5.344 68E-08,從而可以確定20 s采樣時間交通噪聲序列的飽和嵌入維數為6。在混沌預測時,一般選取飽和嵌入維數的1/2作為系統的嵌入維數(當飽和嵌入維數為奇數時,選取飽和嵌入維數1/2的下一位整數作為系統的嵌入維數),因此確定系統的嵌入維數為3。由此可判定,交通噪聲時間序列存在混沌現象。 同理,采樣時間為40 s時,交通噪聲時間序列的飽和嵌入維數也為6,系統的嵌入維數為3。 4.1 混沌預測理論 如果在重構的相空間中,將交通噪聲時間序列特征軌跡恢復,通過對該軌跡的擬合,即可得到映射: X(k+1)=f(X(k)) (12) 式中:X(k)是相空間中的點。 設相空間嵌入維數為m,則: (13) 預測算法如下: 1)確定交通噪聲時間序列的嵌入維數m和延遲時間τ。 2)重構交通噪聲系統, 將時間序列x(n),n=1,2,…,N進行轉化: 式中:k=N-(m-1)τ。由所有向量的分量組成的空間為相空間,交通噪聲時間序列轉化為相空間中的點。 3)尋找最近鄰,假設當前的狀態點為X(j),通過計算各點與X(j)的歐氏距離找出p個最近鄰點X(i1),X(i2),…,X(ip)。 4)找出所有p個最近鄰的下一個相點X(i1+1),X(i2+1),…,X(ip+1)。在這個小鄰域內對相空間軌跡進行線性擬合,即求出下式中的系數A,B: 擬合求得A,B后,通過X(j+1)=A+BX(j)得到相空間中軌跡的趨勢,從而求出交通噪聲時間序列中x(j+1+(m-1)τ)的預測值。 4.2 交通噪聲的混沌預測 根據計算結果,選擇重構相空間的嵌入維數m=3,延遲時間τ=12,對20s采樣時間的交通噪聲時間序列進行相空間重構,得到維數為3的相空間,其中相點個數k=N-(m-1)τ=276。對檢驗集中的60個點進行預測。假設當前的狀態點為X(270),分別計算各點與X(270)的歐氏距離ρ=(X(270)-X(i))(0 建立系數矩陣: 擬合求得A=-0.69,B=1.05。通過公式X(j+1)=A+BX(j)分別求得x301到x360的數值,繪制預測值曲線并與實際值進行比較見圖4。 圖4 預測值與實測值 平均相對誤差: 8.56% 由圖4,實際值和預測值相差不大,城市道路交通噪聲時間序列混沌預測結果平均相對誤差為8.56%,精度較高。同理,對于40 s采樣時間的交通噪聲時間序列進行混沌預測,平均相對誤差為9.33%。 城市道路交通噪聲與多因素相關,筆者采集了交通噪聲時間序列值,應用相空間重構理論獲得了關聯維數和嵌入維數,證明了噪聲序列具有混沌特性。最后利用混沌模型對短時城市道路交通噪聲進行預測和比對,預測精度較高。城市道路交通噪聲的混沌行為是否存在與采樣時間關系不大,但與混沌預測的精度有關。隨著樣本量的增加,相空間中相點的密度相應增加,近鄰相點的選擇會更加合理,預測精度也會提高。 [1] 肖裕民.城市交通滿意度定量化評價方法探討[J].重慶交通大學學報:自然科學版,2009,28(1):111-115. Xiao Yumin.Discussion on quantitative evaluation method of urban traffic satisfaction [J].Journal of Chongqing Jiaotong University:Natural Science,2009,28(1):111-115. [2] 李超,劉小明,榮建.道路交通噪聲計算機仿真模型[J].武漢理工大學學報:交通科學與工程版,2010,34(2):350-353. Li Chao,Liu Xiaoming,Rong Jian.Road traffic noise computer simulation model [J].Journal of Wuhan University of Technology:Transportation Science & Engineering,2009,34(2):350-353. [3] 常玉林,王煒.環形交叉口交通噪聲預測模型[J].交通運輸工程學報,2003,3(1):80-83. Chang Yulin,Wang Wei.Traffic noise forecasting model at roundabout [J].Journal of Traffic and Transportation Engineering,2003,3(1):80-83. [4] Doygun H,Gurun D K.Analyzing and mapping spatial and temporal dynamics of urban traffic noise pollution:a case study in Kahramanmara,Turkey [J].Environmental Monitoring and Assessment,2008,142(1/2/3):65-72. [5] Jamrah A,Al-Omari A,Sharabi R.Evaluation of traffic noise pollution in Amman,Jordan [J].Environmental Monitoring and Assessment,2006,120(1/3):499-525. [6] 韓善靈,朱平,林忠欽.道路交通噪聲評價及預測新方法[J].交通運輸工程學報,2005,5(3):111-114. Han Shanling,Zhu Ping,Lin Zhongqin.Evaluation and prediction new methods of road traffic noise [J].Journal of Traffic and Transportation Engineering,2005,5(3):111-114. [7] 劉小明,李超,榮建.道路交通噪聲預測模型研究[J].北京工業大學學報,2009,35(7):953-959. Liu Xiaoming,Li Chao,Rong Jian.Review in road traffic noise prediction model study [J].Journal of Beijing University of Technology,2009,35(7):953-959. [8] 袁玲.交通噪聲預測的神經網絡模型[J].長安大學學報:自然科學版,2003,23(2):84-87. Yuan Ling.Neural network for predicting traffic noise [J].Journal of Chang’an University:Natural Science Edition,2003,23(2):84-87. [9] 修春波,劉向東,張宇河.相空間重構延遲時間與嵌入維數的選擇[J].北京理工大學學報:自然科學版,2003,23(2):219-224. Xiu Chunbo,Liu Xiangdong,Zhang Yuhe.Selection of embedding dimension and delay time in the phase space reconstruction [J].Tranasaltions of Beijing Institute of Technology:Natural Science Edition,2003,23(2):219-224. [10] 劉力軍,李松,解永樂.短時交通流混沌預測模型的比較研究數學的實踐與認識,2011,41(17):106-114. Liu Lijun,Li Song,Xie Yongle.Comparative study on chaotic prediction model in short-term traffic flow [J].Mathematics in Practice and Theory,2011,41(17):106-114. Chaotic Characteristics and Application of Traffic Noise of Urban Road Zhang Wenhui1, Luo Wenwen1, Li Zhuo2, Xu Huizhi1 (1. School of Traffic, Northeast Forestry University, Harbin 150040, Heilongjiang, China; 2. Department of Automobile Engineering, Beijing Vocational College of Transportation, Beijing 102618, China) Traffic noise was composed of time series, which was collected at certain section in urban road. Autocorrelation function was used to calculate the delay time. When the autocorrelation coefficient attenuated to 0.4, the delay time to reconstruct phase space was 12. The training set included two groups of noise samples was employed to calculate the correlation dimension. When embedding dimension was 6, the correlation dimension kept invariant. Therefore, the embedding dimension of system was 3 and traffic noise samples were of chaotic characteristics. Based on the reconstructed phase space, state points and near points, the fitting parameters were calculated. The two groups of traffic noise samples were predicted respectively by chaotic models and then compared the results with those got by the training set. The results show that chaotic models are suitable to predict the traffic noise of urban road in a short time. The average relative errors of two groups of noise samples were 8.56% and 9.33% individually. traffic engineering; urban road; traffic noise; chaotic characteristics; phase space reconstruction 10.3969/j.issn.1674-0696.2015.01.25 2013-08-09; 2014-01-06 國家自然科學基金項目(51108137) 張文會(1978—),男,黑龍江哈爾濱人,副教授,博士后,主要從事交通環境與安全技術方面的研究。E-mail:rayear@163.com。 U491.9 A 1674-0696(2015)01-116-05
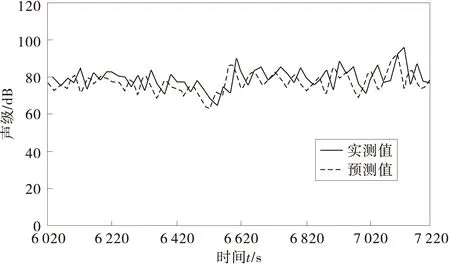
4 城市道路交通噪聲的混沌預測


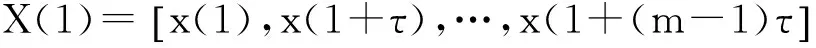
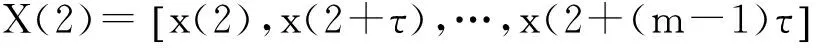

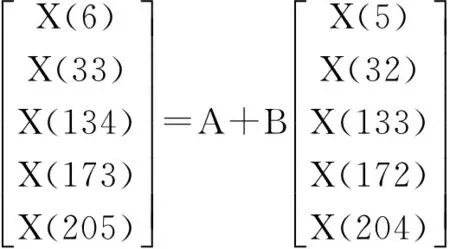
5 結 語

