土地利用結(jié)構(gòu)指標(biāo)新探及計(jì)算程序研究
吳 塹 虹,劉 瓊,段 雪 剛
(中南大學(xué)有色金屬成礦預(yù)測(cè)教育部重點(diǎn)實(shí)驗(yàn)室,地球科學(xué)與信息物理學(xué)院,湖南 長(zhǎng)沙 410083)
?
土地利用結(jié)構(gòu)指標(biāo)新探及計(jì)算程序研究
吳 塹 虹,劉 瓊,段 雪 剛
(中南大學(xué)有色金屬成礦預(yù)測(cè)教育部重點(diǎn)實(shí)驗(yàn)室,地球科學(xué)與信息物理學(xué)院,湖南 長(zhǎng)沙 410083)
針對(duì)目前土地利用結(jié)構(gòu)指標(biāo)眾多,但因?qū)ζ湟饬x及相互間關(guān)系缺少深入分析而出現(xiàn)的普遍復(fù)用現(xiàn)象,選取常用表征土地利用數(shù)量和空間結(jié)構(gòu)的7個(gè)指標(biāo),探討指標(biāo)間相關(guān)性,并對(duì)指標(biāo)意義、分類(lèi)和模型展開(kāi)分析和新的探討。研究表明:原表征土地利用空間格局的多樣性指數(shù)、優(yōu)勢(shì)度指數(shù)和均勻度指數(shù)應(yīng)歸屬于土地利用數(shù)量結(jié)構(gòu)指標(biāo);因同類(lèi)指標(biāo)高度相關(guān),進(jìn)行土地利用結(jié)構(gòu)分析時(shí)在同類(lèi)指標(biāo)中擇一即可,無(wú)需復(fù)用;優(yōu)化的集中化指數(shù)模型簡(jiǎn)化了計(jì)算,且能表達(dá)區(qū)域自身的集中化程度。提出了根據(jù)斑塊形態(tài)差異程度而選擇采用算術(shù)或加權(quán)法進(jìn)行平均分維數(shù)和平均形狀指數(shù)計(jì)算的建議,可使對(duì)斑塊空間形態(tài)特征的測(cè)度更為準(zhǔn)確;創(chuàng)建的基于斑塊拐點(diǎn)數(shù)的形態(tài)指數(shù)模型為描述斑塊形態(tài)復(fù)雜程度提供了新指標(biāo)。針對(duì)目前土地利用結(jié)構(gòu)指標(biāo)計(jì)算軟件大而復(fù)雜、均為英文界面,且不具備計(jì)算數(shù)量結(jié)構(gòu)指標(biāo)的功能,編寫(xiě)了土地利用結(jié)構(gòu)指標(biāo)的計(jì)算程序,可實(shí)現(xiàn)各類(lèi)指標(biāo)的自動(dòng)、快速生成。
土地利用結(jié)構(gòu);指標(biāo);相關(guān)分析;優(yōu)化;創(chuàng)建;計(jì)算程序
近年來(lái),眾多學(xué)者對(duì)土地利用結(jié)構(gòu)特征進(jìn)行了定量研究,從不同角度或方法總結(jié)出了許多定量表征的指標(biāo),但大量有關(guān)土地利用的文獻(xiàn)或報(bào)告普遍存在指標(biāo)復(fù)用現(xiàn)象[1-6]。本文以湖南長(zhǎng)江經(jīng)濟(jì)帶的土地利用數(shù)據(jù)為基礎(chǔ),開(kāi)展土地利用結(jié)構(gòu)各類(lèi)指標(biāo)的定量分析與相關(guān)分析,同時(shí)在大量有關(guān)文獻(xiàn)中隨機(jī)抽取前人相關(guān)的指標(biāo)數(shù)據(jù)進(jìn)行相關(guān)性驗(yàn)證,定量化同類(lèi)指標(biāo)間的相關(guān)程度。在此基礎(chǔ)上對(duì)指標(biāo)意義、分類(lèi)和模型展開(kāi)深入分析和新的探討,對(duì)指標(biāo)分類(lèi)方案進(jìn)行優(yōu)化,對(duì)部分指標(biāo)模型進(jìn)行改進(jìn)并嘗試性地創(chuàng)建新指標(biāo)模型。針對(duì)現(xiàn)有Spatial scaling、Fragstats、APACK、RULE、SIMMAP、Patch Analyst等土地利用結(jié)構(gòu)指標(biāo)計(jì)算軟件缺少土地利用數(shù)量結(jié)構(gòu)指標(biāo)的計(jì)算功能,且存在大型、復(fù)雜、英文界面等不利于基層土地部門(mén)對(duì)其應(yīng)用的不利因素,基于VS201 0平臺(tái)、C#、Microsoft Access 2010進(jìn)行常用指標(biāo)計(jì)算程序的編寫(xiě),實(shí)現(xiàn)對(duì)各類(lèi)土地利用結(jié)構(gòu)指標(biāo)的快速計(jì)算。
1 數(shù)據(jù)來(lái)源及研究方法
1.1 數(shù)據(jù)來(lái)源
數(shù)據(jù)源于湖南長(zhǎng)江經(jīng)濟(jì)帶(包括岳陽(yáng)市的華容縣、君山區(qū)、岳陽(yáng)樓區(qū)、云溪區(qū)、臨湘市和岳陽(yáng)縣共6個(gè)縣市區(qū))2011年土地利用變更數(shù)據(jù)及2011年1∶50 000 數(shù)字化土地利用現(xiàn)狀圖,以及用于驗(yàn)證指標(biāo)相關(guān)性而抽取到的前人[1-5,7-14]相關(guān)的指標(biāo)數(shù)據(jù)。
1.2 研究方法
基于前人對(duì)土地利用結(jié)構(gòu)指標(biāo)的常用分類(lèi),選取多樣化指數(shù)和集中化指數(shù)進(jìn)行土地利用數(shù)量結(jié)構(gòu)分析;選取多樣性指數(shù)、優(yōu)勢(shì)度指數(shù)及均勻度指數(shù)進(jìn)行土地利用空間格局分析;選取分維數(shù)、形狀指數(shù)測(cè)度斑塊空間特征。對(duì)所選取的3類(lèi)7個(gè)指標(biāo)模型進(jìn)行公共因子查找,并將查找出的公共因子進(jìn)行統(tǒng)一表達(dá)處理,定性分析指標(biāo)之間的相關(guān)性。
為定量確定指標(biāo)之間的相關(guān)程度,從湖南長(zhǎng)江經(jīng)濟(jì)帶2011年土地利用變更數(shù)據(jù)中獲取各區(qū)各地類(lèi)面積,并將面積數(shù)據(jù)轉(zhuǎn)換為地類(lèi)面積百分比,從2011年1∶50 000 數(shù)字化土地利用現(xiàn)狀圖的屬性表中獲取斑塊的面積和周長(zhǎng),按照指標(biāo)模型計(jì)算出湖南長(zhǎng)江經(jīng)濟(jì)帶的3類(lèi)7個(gè)指標(biāo),利用SPSS軟件對(duì)3類(lèi)指標(biāo)分別進(jìn)行相關(guān)分析,并結(jié)合前人的指標(biāo)數(shù)據(jù)進(jìn)行相關(guān)性驗(yàn)證(相關(guān)系數(shù)均為筆者應(yīng)用SPSS軟件所獲得)。
在相關(guān)分析基礎(chǔ)上,對(duì)指標(biāo)意義和模型展開(kāi)分析,重新厘定指標(biāo)分類(lèi)。運(yùn)用函數(shù)分析法對(duì)指標(biāo)模型的變量及變量之間的關(guān)系進(jìn)行分析,基于GIS功能并結(jié)合空間形態(tài)基本原理對(duì)部分指標(biāo)模型進(jìn)行優(yōu)化或創(chuàng)建。
2 結(jié)果與分析
2.1 指標(biāo)模型分析
3類(lèi)7個(gè)指標(biāo)模型列于表1,多樣化指數(shù)和集中化指數(shù)模型顯示二者的自變量數(shù)量及意義雖不同,但其自變量均只涉及地類(lèi)面積百分比和地類(lèi)數(shù)兩個(gè)公共因子;多樣性指數(shù)、優(yōu)勢(shì)度指數(shù)和均勻度指數(shù)同樣也只涉及地類(lèi)面積百分比和地類(lèi)數(shù)兩個(gè)公共因子,且這3個(gè)指標(biāo)模型的表達(dá)式形似,符合數(shù)學(xué)上線性函數(shù)的表達(dá);而分維數(shù)與形狀指數(shù)的自變量均只涉及斑塊面積和周長(zhǎng)。由此表明同類(lèi)結(jié)構(gòu)指標(biāo)之間應(yīng)存在相關(guān)性,下文將通過(guò)相關(guān)分析對(duì)各類(lèi)指標(biāo)相關(guān)性進(jìn)行定量測(cè)度。
2.2 各類(lèi)指標(biāo)相關(guān)性分析
2.2.1 數(shù)量結(jié)構(gòu)指標(biāo)相關(guān)性 多樣化指數(shù)和集中化指數(shù)相關(guān)分析結(jié)果(表2)表明二者呈現(xiàn)高度負(fù)相關(guān),其中,湖南長(zhǎng)江經(jīng)濟(jì)帶二者的相關(guān)系數(shù)為-0.979,其它地區(qū)的相關(guān)系數(shù)均在-0.95左右,表明二者在定量測(cè)度土地利用數(shù)量結(jié)構(gòu)上所起作用相同,互為補(bǔ)充。
表1 指標(biāo)模型
Table 1 List of index models
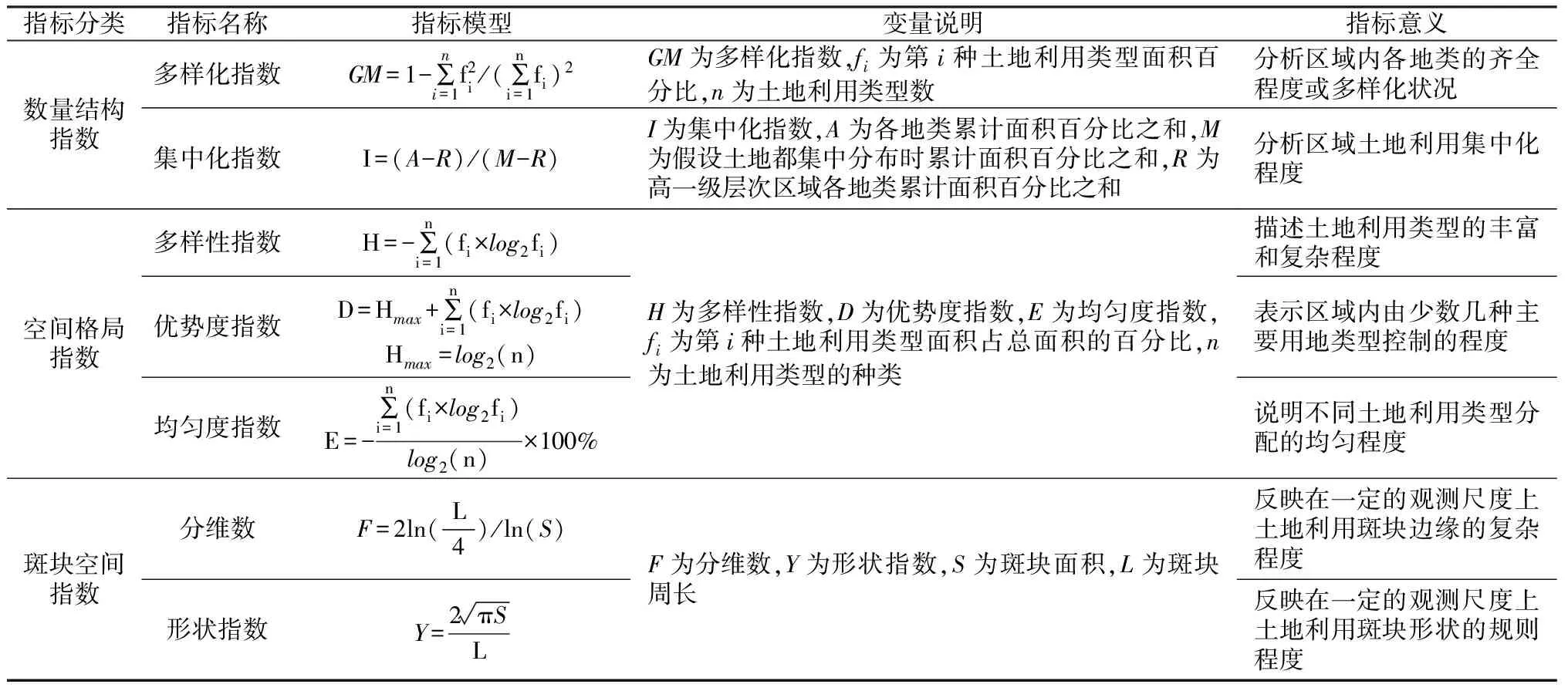
指標(biāo)分類(lèi)指標(biāo)名稱(chēng)指標(biāo)模型變量說(shuō)明指標(biāo)意義數(shù)量結(jié)構(gòu)指數(shù)空間格局指數(shù)斑塊空間指數(shù)多樣化指數(shù)GM=1-∑ni=1f2i/(∑ni=1fi)2集中化指數(shù)I=(A-R)/(M-R)多樣性指數(shù)H=-∑ni=1(fi×log2fi)優(yōu)勢(shì)度指數(shù)D=Hmax+∑ni=1(fi×log2fi)Hmax=log2(n)均勻度指數(shù)E=-∑ni=1(fi×log2fi)log2(n)×100%分維數(shù)F=2ln(L4)/ln(S)形狀指數(shù)Y=2πSLGM為多樣化指數(shù),fi為第i種土地利用類(lèi)型面積百分比,n為土地利用類(lèi)型數(shù)I為集中化指數(shù),A為各地類(lèi)累計(jì)面積百分比之和,M為假設(shè)土地都集中分布時(shí)累計(jì)面積百分比之和,R為高一級(jí)層次區(qū)域各地類(lèi)累計(jì)面積百分比之和H為多樣性指數(shù),D為優(yōu)勢(shì)度指數(shù),E為均勻度指數(shù),fi為第i種土地利用類(lèi)型面積占總面積的百分比,n為土地利用類(lèi)型的種類(lèi)F為分維數(shù),Y為形狀指數(shù),S為斑塊面積,L為斑塊周長(zhǎng)分析區(qū)域內(nèi)各地類(lèi)的齊全程度或多樣化狀況分析區(qū)域土地利用集中化程度描述土地利用類(lèi)型的豐富和復(fù)雜程度表示區(qū)域內(nèi)由少數(shù)幾種主要用地類(lèi)型控制的程度說(shuō)明不同土地利用類(lèi)型分配的均勻程度反映在一定的觀測(cè)尺度上土地利用斑塊邊緣的復(fù)雜程度反映在一定的觀測(cè)尺度上土地利用斑塊形狀的規(guī)則程度
表2 多樣化指數(shù)和集中化指數(shù)相關(guān)系數(shù)
Table 2 Correlation coefficient of Gibbs-Martin index and centralization index
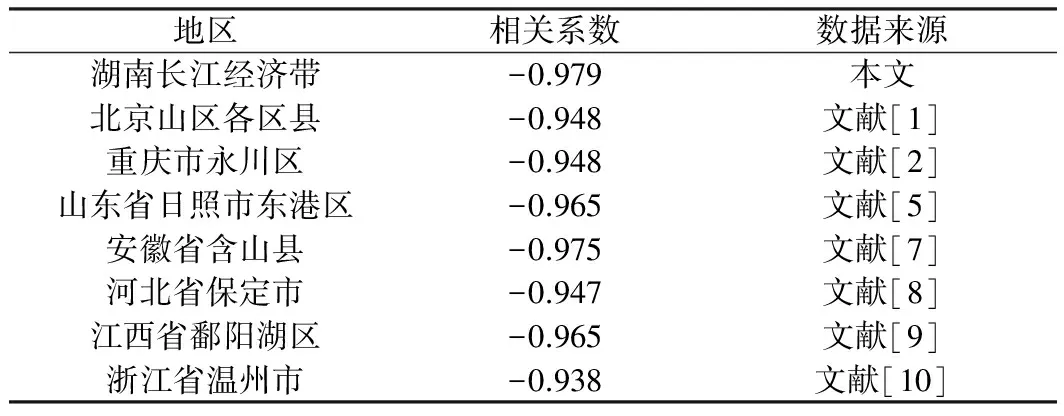
地區(qū)相關(guān)系數(shù)數(shù)據(jù)來(lái)源湖南長(zhǎng)江經(jīng)濟(jì)帶-0.979本文北京山區(qū)各區(qū)縣-0.948文獻(xiàn)[1]重慶市永川區(qū)-0.948文獻(xiàn)[2]山東省日照市東港區(qū)-0.965文獻(xiàn)[5]安徽省含山縣-0.975文獻(xiàn)[7]河北省保定市-0.947文獻(xiàn)[8]江西省鄱陽(yáng)湖區(qū)-0.965文獻(xiàn)[9]浙江省溫州市-0.938文獻(xiàn)[10]
2.2.2 空間格局指標(biāo)相關(guān)性 土地利用多樣性指數(shù)、優(yōu)勢(shì)度指數(shù)和均勻度指數(shù)相關(guān)分析結(jié)果(表3)表明,多樣性指數(shù)與優(yōu)勢(shì)度指數(shù)呈高度負(fù)相關(guān),二者相關(guān)系數(shù)介于-0.979~-1;優(yōu)勢(shì)度指數(shù)與均勻度指數(shù)呈高度負(fù)相關(guān),相關(guān)系數(shù)介于-0.984~-1;多樣性指數(shù)與均勻度指數(shù)則呈高度正相關(guān),相關(guān)系數(shù)均在0.99左右。說(shuō)明這3個(gè)指數(shù)從不同的側(cè)面反映同一個(gè)問(wèn)題,互為驗(yàn)證。
表3 多樣性指數(shù)、優(yōu)勢(shì)度指數(shù)和均勻度指數(shù)相關(guān)系數(shù)
Table 3 Correlation coefficient of diversity index,dominance index and evenness index
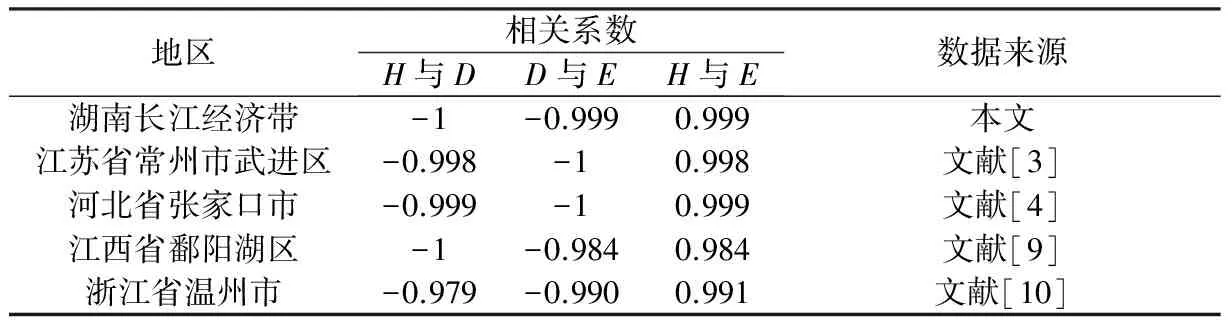
地區(qū)相關(guān)系數(shù)H與DD與EH與E數(shù)據(jù)來(lái)源湖南長(zhǎng)江經(jīng)濟(jì)帶-1-0.9990.999本文江蘇省常州市武進(jìn)區(qū)-0.998-10.998文獻(xiàn)[3]河北省張家口市-0.999-10.999文獻(xiàn)[4]江西省鄱陽(yáng)湖區(qū)-1-0.9840.984文獻(xiàn)[9]浙江省溫州市-0.979-0.9900.991文獻(xiàn)[10]
2.2.3 斑塊空間指標(biāo)相關(guān)性 分維數(shù)和形狀指數(shù)相關(guān)分析結(jié)果見(jiàn)表4,對(duì)湖南長(zhǎng)江經(jīng)濟(jì)帶和安徽省含山縣各地類(lèi)平均分維數(shù)和形狀指數(shù)做相關(guān)分析,結(jié)果顯示二者呈高度負(fù)相關(guān)。此外,對(duì)湖南長(zhǎng)江經(jīng)濟(jì)帶和吉林省長(zhǎng)嶺縣各地類(lèi)的分維數(shù)和形狀指數(shù)分別做相關(guān)分析,發(fā)現(xiàn)除湖南長(zhǎng)江經(jīng)濟(jì)帶中受人類(lèi)活動(dòng)干擾最強(qiáng)的城鎮(zhèn)村及工礦用地二者的相關(guān)系數(shù)為-0.649(中度負(fù)相關(guān))外,其它地類(lèi)二者的相關(guān)系數(shù)介于-0.931~-0.992,為高度負(fù)相關(guān)。由此得出分維數(shù)和形狀指數(shù)高度負(fù)相關(guān)的結(jié)論,兩者在定量表征斑塊形態(tài)的復(fù)雜程度上所起的作用一致。
表4 分維數(shù)和形狀指數(shù)相關(guān)系數(shù)
Table 4 Correlation coefficient of fractal dimension and shape index

地區(qū)相關(guān)系數(shù)備注數(shù)據(jù)來(lái)源湖南長(zhǎng)江經(jīng)濟(jì)帶-0.987安徽省含山縣-0.805湖南長(zhǎng)江經(jīng)濟(jì)帶-0.649,-0.931~-0.983吉林省長(zhǎng)嶺縣-0.957~-0.992各地類(lèi)平均分維數(shù)和形狀指數(shù)做相關(guān)分析各地類(lèi)分維數(shù)和形狀指數(shù)分別做相關(guān)分析本文文獻(xiàn)[7]本文文獻(xiàn)[11]
2.2.4 指標(biāo)相關(guān)性分析意義 各類(lèi)指標(biāo)相關(guān)性分析表明,同類(lèi)指標(biāo)高度相關(guān),各類(lèi)指標(biāo)在相應(yīng)測(cè)度的土地利用數(shù)量或空間結(jié)構(gòu)上所起的作用相同,互為補(bǔ)充和驗(yàn)證。在土地利用結(jié)構(gòu)分析的實(shí)際工作中若對(duì)每個(gè)指標(biāo)都進(jìn)行計(jì)算,不僅加大了工作量,而且會(huì)使得對(duì)土地利用結(jié)構(gòu)特征的描述復(fù)雜化。筆者建議在進(jìn)行土地利用結(jié)構(gòu)分析時(shí)同類(lèi)指標(biāo)擇一即可,無(wú)需復(fù)用。此外,在進(jìn)行土地利用結(jié)構(gòu)分析時(shí),應(yīng)根據(jù)實(shí)際需要和側(cè)重點(diǎn)選取指標(biāo)。當(dāng)欲強(qiáng)調(diào)區(qū)域地類(lèi)的豐富程度時(shí),可選擇多樣化指數(shù)或多樣性指數(shù);當(dāng)擬強(qiáng)調(diào)區(qū)域地類(lèi)集中程度時(shí),可選擇集中化指數(shù)或優(yōu)勢(shì)度指數(shù);而要強(qiáng)調(diào)區(qū)域不同地類(lèi)分配的均勻程度時(shí),可選擇均勻度指數(shù);分析斑塊形態(tài)的復(fù)雜程度時(shí),則可選擇分維數(shù)或形狀指數(shù)。
2.3 空間格局指標(biāo)重新分類(lèi)
多樣化指數(shù)、集中化指數(shù)與多樣性指數(shù)、優(yōu)勢(shì)度指數(shù)和均勻度指數(shù)的公共因子均為地類(lèi)面積百分比和地類(lèi)數(shù)。此外,雖然這兩類(lèi)指標(biāo)分屬于數(shù)量、空間結(jié)構(gòu)指標(biāo),但其表達(dá)的意義相似,應(yīng)有密切相關(guān)性。在兩類(lèi)指標(biāo)中分別選取一個(gè)指標(biāo)進(jìn)行跨類(lèi)相關(guān)分析,以確定其相關(guān)程度,結(jié)果見(jiàn)表5。
表5 多樣化指數(shù)和多樣性指數(shù)相關(guān)系數(shù)
Table 5 Correlation coefficient of Gibbs-Martin index and diversity index

地區(qū)相關(guān)系數(shù)數(shù)據(jù)來(lái)源湖南長(zhǎng)江經(jīng)濟(jì)帶0.991本文江西省鄱陽(yáng)湖區(qū)0.976文獻(xiàn)[9]浙江省溫州市0.989文獻(xiàn)[10]
相關(guān)性計(jì)算表明多樣化和多樣性指數(shù)呈高度正相關(guān)。其它指數(shù)的兩兩相關(guān)分析(因篇幅原因,不一一列表)的相關(guān)系數(shù)絕對(duì)值也均在0.9以上,故得出兩類(lèi)指標(biāo)間存在高度相關(guān)性。基于兩類(lèi)指標(biāo)間存在高度相關(guān)性、指標(biāo)模型的公共因子均為地類(lèi)面積百分比和地類(lèi)數(shù)以及指標(biāo)意義相近,筆者認(rèn)為原表征土地空間格局的多樣性指數(shù)、優(yōu)勢(shì)度指數(shù)和均勻度指數(shù)用于表達(dá)土地利用數(shù)量結(jié)構(gòu)更為合適。
2.4 部分指標(biāo)優(yōu)化
2.4.1 集中化指數(shù)的優(yōu)化 對(duì)集中化指數(shù)模型進(jìn)行分析,發(fā)現(xiàn)該指標(biāo)是通過(guò)建立區(qū)域與上級(jí)區(qū)域的土地利用集中化程度的關(guān)系來(lái)表征區(qū)域的集中化程度,而其他表征數(shù)量結(jié)構(gòu)的指標(biāo)均未涉及上級(jí)區(qū)域,均為區(qū)域本身的數(shù)量結(jié)構(gòu),因此表征土地利用數(shù)量結(jié)構(gòu)的指標(biāo)間不具有可比性。此外,集中化指數(shù)不能獨(dú)立表達(dá)區(qū)域本身的集中化程度,且其模型表達(dá)式盡管簡(jiǎn)單,但其包含3個(gè)變量,這些變量還暗含2個(gè)次級(jí)變量,故其計(jì)算繁瑣。對(duì)原有模型進(jìn)行優(yōu)化,其表達(dá)式為:
I優(yōu)=A/n
式中:A仍為各地類(lèi)(按照地類(lèi)面積百分比由高到低順序排列,即對(duì)地類(lèi)面積百分比進(jìn)行Huffman編碼)累計(jì)面積百分比之和,n為土地利用類(lèi)型數(shù)。
優(yōu)化后的模型變量數(shù)由原來(lái)的5個(gè)減至2個(gè),大大簡(jiǎn)化了計(jì)算,而且能獨(dú)立、準(zhǔn)確地表達(dá)區(qū)域自身的集中化程度。
2.4.2 平均分維數(shù)和平均形狀指數(shù)的優(yōu)化 前人在計(jì)算某一地類(lèi)或區(qū)域的平均分維數(shù)和平均形狀指數(shù)時(shí),多采用該地類(lèi)或區(qū)域所有斑塊的分維數(shù)和形狀指數(shù)的算術(shù)平均值,這種處理方法在某一地類(lèi)或區(qū)域內(nèi)各斑塊形態(tài)接近時(shí)具有簡(jiǎn)便的優(yōu)點(diǎn)。但在實(shí)際情況中,某一地類(lèi)或區(qū)域內(nèi)的斑塊形態(tài)一般存在不定差異,其差異主要體現(xiàn)為斑塊面積及周長(zhǎng)大小的不同,筆者認(rèn)為為了更準(zhǔn)確地表達(dá)某一地類(lèi)或區(qū)域的平均分維數(shù)和平均形狀指數(shù),可將斑塊面積及周長(zhǎng)作為權(quán)重因子加入到計(jì)算中。其表達(dá)式為:
F均=∑(Fw) ,Y均=∑(Yw)
式中:F均、Y均分別為某一地類(lèi)或區(qū)域的平均分維數(shù)、平均形狀指數(shù);F、Y分別為斑塊分維數(shù)、斑塊形狀指數(shù);w為斑塊綜合權(quán)重,其模型可表達(dá)為:
w=w1(Li/∑Li)+w2(Si/∑Si)
式中:w1為斑塊長(zhǎng)度權(quán)重系數(shù),w2為斑塊面積權(quán)重系數(shù),Li為第i種地類(lèi)或區(qū)域單個(gè)斑塊長(zhǎng)度,Si為第i種地類(lèi)或區(qū)域單個(gè)斑塊面積。
顯然當(dāng)某一地類(lèi)或區(qū)域內(nèi)的斑塊形態(tài)存在較大差異時(shí),加權(quán)平均法計(jì)算結(jié)果更貼近真實(shí)情況,但該方法的缺點(diǎn)是計(jì)算量明顯增加,且權(quán)重系數(shù)的確定有層次分析法、綜合評(píng)價(jià)法和專(zhuān)家評(píng)價(jià)法等多種方法,也使工作量大大增加,但增加的工作量可以通過(guò)編程方法實(shí)現(xiàn)自動(dòng)計(jì)算來(lái)解決(有待進(jìn)一步研究)。所以筆者建議在開(kāi)展研究斑塊空間形態(tài)特征的工作時(shí),應(yīng)先對(duì)同一地類(lèi)或區(qū)域內(nèi)的所有斑塊面積或周長(zhǎng)做頻率分布直方圖,若頻率分布直方圖服從或近似服從正態(tài)分布,則可采用算術(shù)平均法;反之,則應(yīng)采用加權(quán)平均法。
2.5 新指標(biāo)創(chuàng)建嘗試
分維數(shù)、形狀指數(shù)是最常見(jiàn)的測(cè)度斑塊形態(tài)特征的指標(biāo),其模型中均只包含斑塊面積和周長(zhǎng)兩個(gè)因子。實(shí)際上斑塊的拐點(diǎn)數(shù)同樣可以反映斑塊形態(tài)的復(fù)雜程度,且單位周長(zhǎng)或面積上的拐點(diǎn)數(shù)越多斑塊形態(tài)越趨復(fù)雜。現(xiàn)有的GIS軟件具有自動(dòng)提取斑狀拐點(diǎn)數(shù)的功能,因此筆者認(rèn)為可以斑狀拐點(diǎn)數(shù)作為變量,構(gòu)建斑塊形態(tài)指數(shù)模型,其表達(dá)式為:
T=N/ln(L) 或T=N/ln(S)
式中:T為斑塊形態(tài)指數(shù),N為斑塊的拐點(diǎn)數(shù),L為斑塊的長(zhǎng)度,S為斑塊的面積。
在計(jì)算某一地類(lèi)或區(qū)域的平均形態(tài)指數(shù)時(shí),先進(jìn)行相關(guān)優(yōu)化,若要采用加權(quán)平均法,則需構(gòu)建權(quán)重模型。斑塊權(quán)重w模型為:
w=Li/∑Li或w=Si/∑Si
式中:Li為第i種地類(lèi)或區(qū)域單個(gè)斑塊長(zhǎng)度,Si為第i種地類(lèi)或區(qū)域單個(gè)斑塊面積。
原有的分維數(shù)、形狀指數(shù)是基于周長(zhǎng)-面積法,創(chuàng)建的形態(tài)指數(shù)是基于拐點(diǎn)數(shù)-周長(zhǎng)法或拐點(diǎn)數(shù)-面積法,而數(shù)學(xué)上曲線的凹凸用拐點(diǎn)表達(dá),故筆者認(rèn)為該法在定量測(cè)度斑塊形態(tài)特征上更為準(zhǔn)確。
3 土地利用結(jié)構(gòu)指標(biāo)計(jì)算程序開(kāi)發(fā)
基于VS2010平臺(tái)、C#、Microsoft Access 2010進(jìn)行土地利用結(jié)構(gòu)指標(biāo)計(jì)算程序開(kāi)發(fā)。基于各參數(shù)的關(guān)聯(lián)性,繪制E-R圖(圖1),數(shù)據(jù)庫(kù)包括行政區(qū)各地類(lèi)面積表(從土地利用變更數(shù)據(jù)中獲取)和各地類(lèi)斑塊表(從土地利用現(xiàn)狀圖的屬性表中獲取,提取面積和周長(zhǎng))。根據(jù)數(shù)據(jù)流程(圖2)分析,采用C#提供“OleDb”接口實(shí)現(xiàn)對(duì)Access數(shù)據(jù)庫(kù)連接及功能集成。基于人-機(jī)友好原則將復(fù)雜的指標(biāo)計(jì)算功能設(shè)置于后臺(tái)運(yùn)行,實(shí)現(xiàn)使用者在界面對(duì)擬計(jì)算的指標(biāo)進(jìn)行勾選就可自動(dòng)完成計(jì)算,且結(jié)果數(shù)據(jù)以表格形式自動(dòng)展示,并可以Excel格式導(dǎo)出(圖3)。
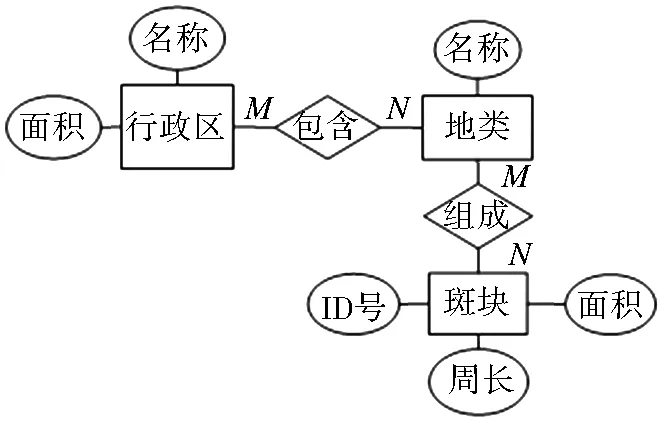
圖1 E-R圖
Fig.1 E-R diagram
4 結(jié)論
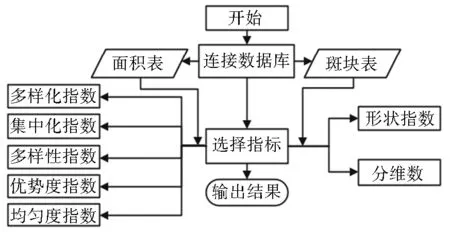
圖2 土地利用結(jié)構(gòu)指標(biāo)計(jì)算程序流程
Fig.2 Calculation program flowchart of land use structure indices
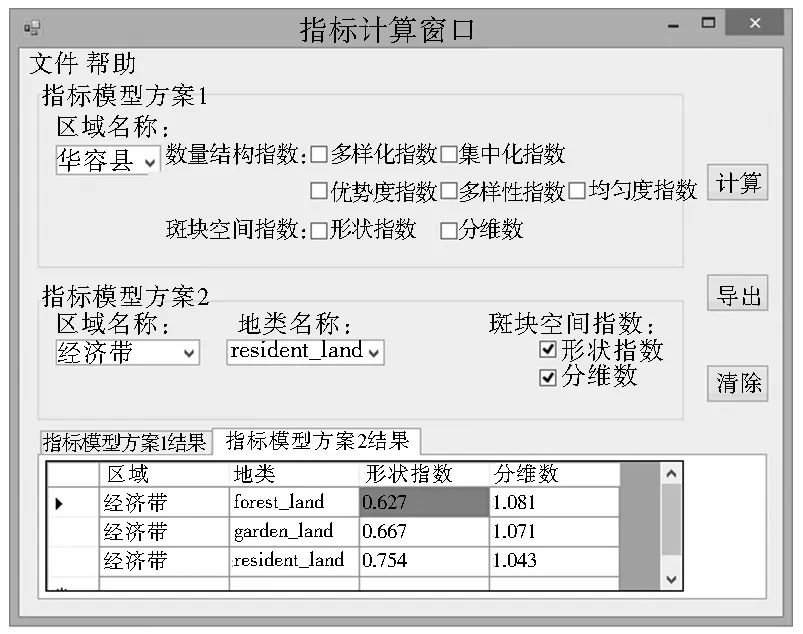
圖3 土地利用結(jié)構(gòu)指標(biāo)計(jì)算程序界面
Fig.3 Calculation program interface of land use structure indices
以湖南長(zhǎng)江經(jīng)濟(jì)帶為例,同時(shí)結(jié)合前人的指標(biāo)數(shù)據(jù),開(kāi)展對(duì)土地利用結(jié)構(gòu)常用指標(biāo)的重新認(rèn)識(shí)、優(yōu)化及指標(biāo)自動(dòng)計(jì)算等工作,結(jié)論如下: 1)原表征土地空間格局的多樣性指數(shù)、優(yōu)勢(shì)度指數(shù)和均勻度指數(shù)應(yīng)歸屬于土地利用數(shù)量結(jié)構(gòu)指標(biāo),因同類(lèi)指標(biāo)高度相關(guān),進(jìn)行土地利用結(jié)構(gòu)分析時(shí)同類(lèi)指標(biāo)擇一即可,無(wú)需復(fù)用;2)集中化指數(shù)模型的優(yōu)化不僅具有表達(dá)及計(jì)算簡(jiǎn)單的優(yōu)勢(shì),而且能獨(dú)立且準(zhǔn)確表達(dá)區(qū)域自身的集中化程度;3)提出的根據(jù)斑塊周長(zhǎng)或面積頻率分布直方圖特征選擇采用算術(shù)平均法或加權(quán)平均法進(jìn)行平均分維數(shù)和平均形狀指數(shù)計(jì)算的建議,使得對(duì)斑塊空間形態(tài)特征的測(cè)度更為準(zhǔn)確;4)創(chuàng)建的基于斑塊單位長(zhǎng)度或面積上的拐點(diǎn)數(shù)的斑塊形態(tài)指數(shù)模型,為描述斑塊形態(tài)復(fù)雜程度提供了新的參考指標(biāo);5)計(jì)算程序?yàn)橹形慕缑妗⑵脚_(tái)簡(jiǎn)單、操作可行,實(shí)現(xiàn)了土地利用結(jié)構(gòu)指標(biāo)的自動(dòng)、快速生成,具有應(yīng)用價(jià)值。
中南大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院侯木舟教授對(duì)本文提出了專(zhuān)業(yè)指導(dǎo),此致謝忱!
[1] 王秀麗,關(guān)小克,薛劍.北京山區(qū)區(qū)縣土地利用結(jié)構(gòu)定量分析及農(nóng)業(yè)產(chǎn)業(yè)研究[J].中國(guó)農(nóng)業(yè)資源與區(qū)劃,2013,34(2):85-91.
[2] 施開(kāi)放.西南丘陵山區(qū)縣域土地利用結(jié)構(gòu)特征研究——以重慶市永川區(qū)為例[D].重慶:西南大學(xué),2013.
[3] 張群,張?chǎng)?李飛雪,等.基于信息熵和數(shù)據(jù)包絡(luò)分析的區(qū)域土地利用結(jié)構(gòu)評(píng)價(jià)——以常州市武進(jìn)區(qū)為例[J].長(zhǎng)江流域資源與環(huán)境,2013,22(9):1149-1155.
[4] 郭洪峰,許月卿,田媛.張家口市土地利用結(jié)構(gòu)特征及其動(dòng)態(tài)變化[J].水土保持通報(bào),2013,33(3):259-264.
[5] 魏魯,張?zhí)m梅,郭晨.日照市東港區(qū)土地利用結(jié)構(gòu)與空間布局分析[J].山東國(guó)土資源,2011,27(3):54-56.
[6] 林源,劉木生,林聯(lián)盛,等.贛州市土地利用結(jié)構(gòu)定量分析[J].江西科學(xué),2009,27(3):360-364.
[7] 陳其春,呂成文,李壁成,等.縣級(jí)尺度土地利用結(jié)構(gòu)特征定量分析[J].農(nóng)業(yè)工程學(xué)報(bào),2009,25(1):223-231.
[8] 趙志革,趙明,楊慶朋.保定市土地利用結(jié)構(gòu)定量分析[J].江西農(nóng)業(yè)學(xué)報(bào),2007,19(11):89-92.
[9] 劉桃菊,蔡海生,邵建英,等.鄱陽(yáng)湖區(qū)的土地利用結(jié)構(gòu)定量分析[J].江西農(nóng)業(yè)大學(xué)學(xué)報(bào),2003,25(6): 934-938.
[10] 朱鳳武,彭補(bǔ)拙,丁建中,等.溫州市土地利用空間格局研究[J].經(jīng)濟(jì)地理,2001,21(1):102-104.
[11] 王平,盧珊,楊桃,等.地理圖形信息分析方法及其在土地利用研究中的應(yīng)用[J].東北師范大學(xué)學(xué)報(bào)(自然科學(xué)版),2002,34(1):93-99.
[12] 王愛(ài)民,劉加林,繆磊磊,等.人地關(guān)系研究中的土地利用特征指標(biāo)分析[J].經(jīng)濟(jì)地理,1999,19(1):62-66.
[13] 傅伯杰.黃土區(qū)農(nóng)業(yè)景觀空間格局分析[J].生態(tài)學(xué)報(bào),1995,15(2):113-120.
[14] 曹天邦,朱曉華,肖彬,等.土地利用類(lèi)型分布的分形結(jié)構(gòu)及其應(yīng)用——以江蘇省揚(yáng)中縣豐裕鎮(zhèn)為例[J].地域研究與開(kāi)發(fā),1999,18(4):9-12.
New Exploration and Calculation Program Research of Land Use Structure Indices
WU Qian-hong,LIU Qiong,DUAN Xue-gang
(KeyLaboratoryofMetallogenicPredictionofNonferrousMetals,MinistryofEducation,SchoolofGeosciencesandInfo-Physics,CentralSouthUniversity,Changsha410083,China)
In view of the current there are many indices for land use structure,the lack of deep analysis of their significance and mutual relations results in widespread mix-use.The authors selected 7 indices which were commonly used to express the quantitative and spatial structure of land use to investigate the correlation between the indices.In addition,expanding analysis and new exploration in significance,classification and model of the indices were done.Result shows: diversity index,dominance index and evenness index which were used to express the spatial pattern of land use should be attributed to the quantitative structure indicators of land use.Owing to the high correlation between similar indices,one index of similar indices should be selected to analyze structure of land use without mix-use.The optimized centralization index model can simplify the calculation,and can express the extent of its own regional centralization.According to the differences degree in plaque morphology,the arithmetic method or the weighted average method should be chosen to calculate the average fractal dimension and the average shape index.This proposal makes plaque morphology measure more accurate.The created morphology index model which is based on the number of inflection of plaque provides a new index to describe the complexity of plaque morphology.The present calculation softwares of land use structure indices are large,complex,English interface,and can′t calculate the indices of quantitative structure.The paper programs calculation procedure of land use structure indices,various types of indices of land use structure can be automatically and quickly calculated.
land use structure;indices;correlation analysis;optimization;creation;calculation procedures
2014-04-30;
2014-08-05
湘江水環(huán)境重金屬污染整治關(guān)鍵技術(shù)研究與綜合示范項(xiàng)目(2009ZX07212-001-06)
吳塹虹(1957-),女,博士,教授,主要從事GIS教學(xué)及其在地學(xué)中的應(yīng)用研究。 E-mail:qhwu19@163.com
10.3969/j.issn.1672-0504.2015.01.023
F301.23;TP319
A
1672-0504(2015)01-0110-05
- 地理與地理信息科學(xué)的其它文章
- 基于三角形驅(qū)動(dòng)的機(jī)載LiDAR數(shù)據(jù)柵格化算法
- 城市社區(qū)空間應(yīng)急疏散能力評(píng)價(jià)模型構(gòu)建及其應(yīng)用
——以北京市交道口社區(qū)為例 - 土地利用圖綜合質(zhì)量評(píng)價(jià)研究
- 基于GIS的區(qū)域群發(fā)性降雨型滑坡時(shí)空預(yù)報(bào)研究
- 基于歷史數(shù)據(jù)的中國(guó)臺(tái)風(fēng)災(zāi)害孕災(zāi)環(huán)境敏感性分析
- 熱帶季節(jié)雨林和次生林水源涵養(yǎng)服務(wù)價(jià)值變化過(guò)程研究

