低音速氣動彈性機翼的主動控制
仇磊
(江蘇科技大學 電子信息學院,江蘇 鎮江 212003)
近年來,氣動彈性控制系統已經成為了一個重要的研究課題[1],并取得了許多的成果。一系列的論文考慮單輸入單輸出氣動彈性控制問題[2],即副翼偏轉用來控制俯仰角,同時浮沉位移不需要控制而漸近穩定;或者是用它來控制浮沉位移,同時俯仰角自行漸近穩定。而后,一些學者研究基于反饋線性化理論的氣動彈性的控制[3-6],然而,氣動彈性系統是相當復雜的系統,它的精確模型是非常難以制定的,所以通常帶有一定的誤差。文中介紹了以滑模控制和抑制抖振的模糊控制相結合的控制器,并有效地抑制了顫振。
1 非線性氣動彈性機翼控制系統模型
典型的氣動彈性機翼部分的顫振抑制問題,見圖1。這種類型的模型已經成為二維氣彈機翼行為的理論分析和實驗的經典。其中,彈性軸的位置和對俯仰運動的各種類型的剛度是真實的特定值。
氣動彈性機翼的運動方程可以描述為
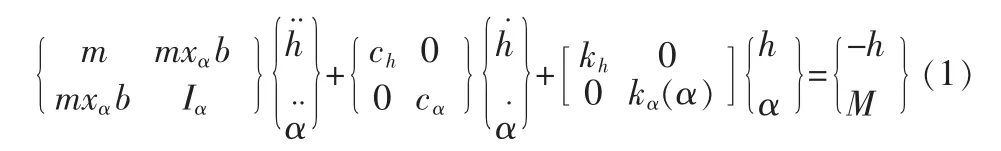
h代表著浮沉運動位移,α是俯仰角,xα是重心和彈性軸的距離,m代表翼的質量,c代表著結構阻尼系數,L和M代表著空氣動力學升力和力矩。
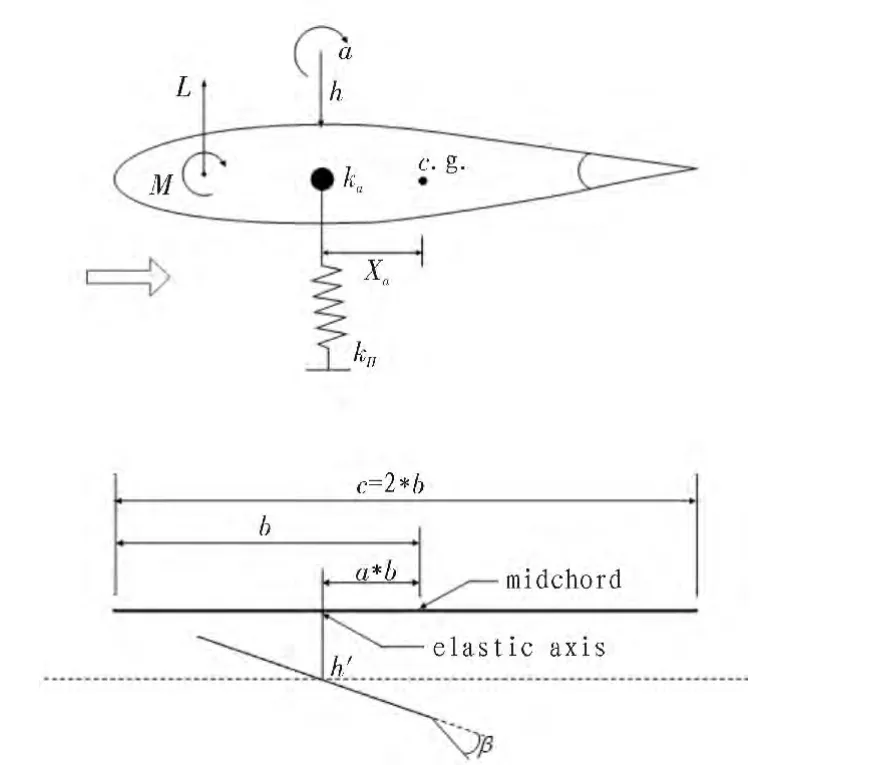
圖1 二元非線性氣動彈性機翼模型Fig.1 Nonlinear aeroelastic two-dimensional wing model
假設擬定的氣動升力和力矩為:
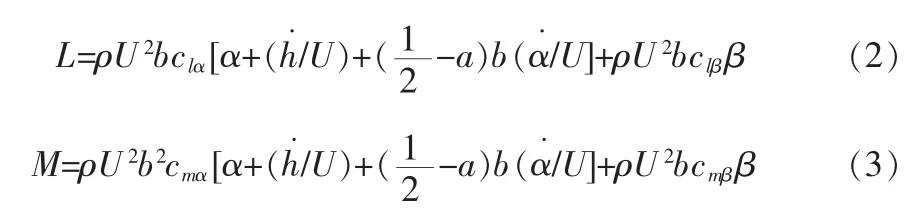
其中,clα和 cmα是每攻角的升力和力矩系數 ,clβ和 cmβ是每控制面偏轉升力和力矩。
結合公式(1)、公式(2)、公式(3),可以得到運動方程為
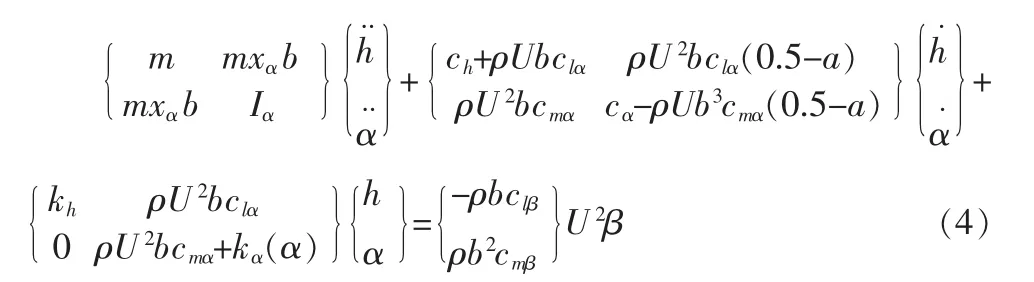
為了簡化形式,引入幾個輔助變量,如式5所示。
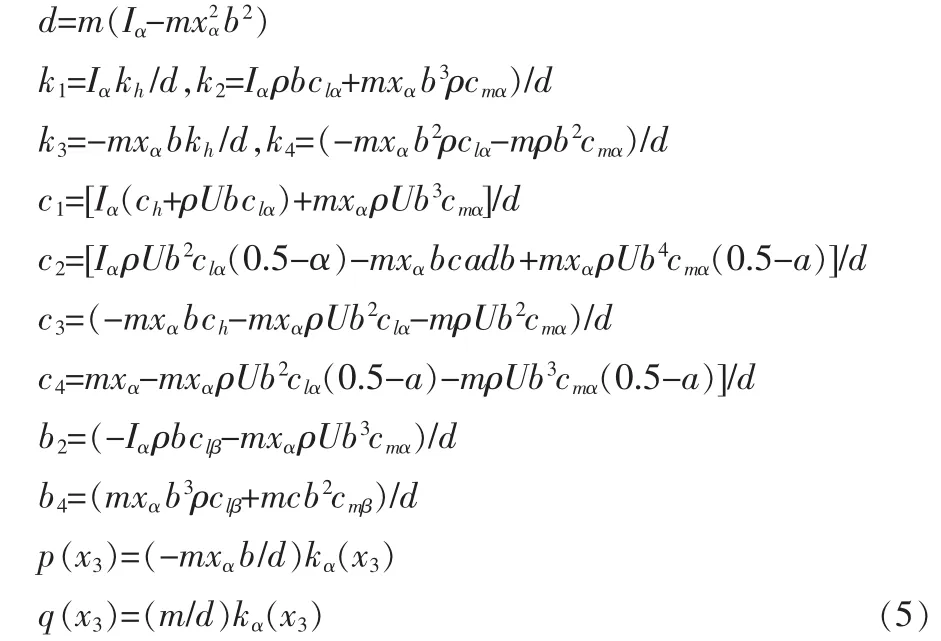
定義狀態變量為
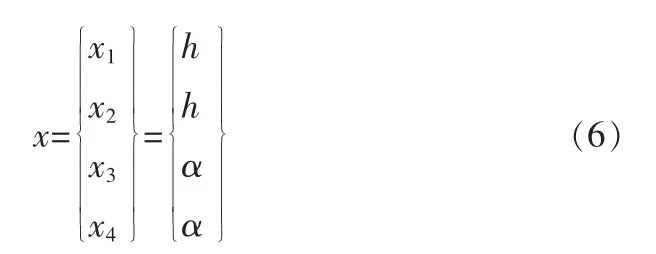
則運動方程變為:

其中,
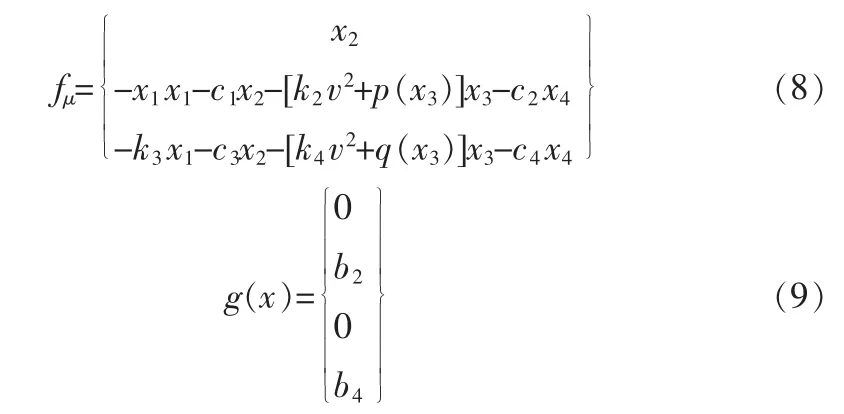
2 模糊滑模控制(FSMC)
實際系統都存在一些不確定因素,例如,參數變化、受到外部環境的擾動及復雜系統的攝動影響等,這些攝動可能包括許多項,數學表達式復雜,對于機翼系統引入滑模控制,使得這樣的攝動對構造的滑動模態完全不影響,即滑動模態對攝動具有“完全自適應性”,保證系統具有很強的魯棒性。
但滑模控制也存在著一些問題。最突出的問題就是抖振問題。對于一個理想的滑模變結構控制系統,假設“結構”切換的過程具有理想開關特性(無時間及空間滯后),系統狀態測量精確無誤,控制量不受限制,則滑動模態總是降維的光滑運動并且漸近穩定于原點,不會出現抖振。但對于一個實際的機翼滑模系統,控制量總是有限的,從而使系統的加速度有限;另外系統存在慣性,切換開關的時間空間滯后及狀態檢測的誤差,所以抖振是必定存在的,而且它可能激發起機翼系統的未建模高頻特性,引起系統性能變差,甚至使系統不穩定。本文引入智能控制方法與之相結合以消除滑模控制的抖振特性,從而結合滑模控制和智能控制的優點,達到更好的控制特性。
首先,將氣動彈性系統視為兩個獨立子系統,每個子系統由單獨的滑模面控制。定義滑模面Sh=S2+λh·S1
其中
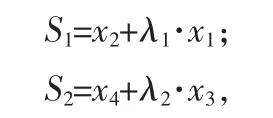
λ1,λ2和λh是正常量。滑模面的斜率λh控制狀態的瞬態響應。FSMC控制的目的是讓系統的滑模面接近零。在這種情況下,滑動面的變量s1和s2將同時收斂到零,然后這兩個子系統(x1,x2)和(x3,x4)也會同時收斂到零。
如圖2所示,給出了FSMC控制系統,其中包括兩個模糊推理系統,斜率推理規則和模糊滑模控制規則。滑模面的斜率在兩個系統中非常重要。
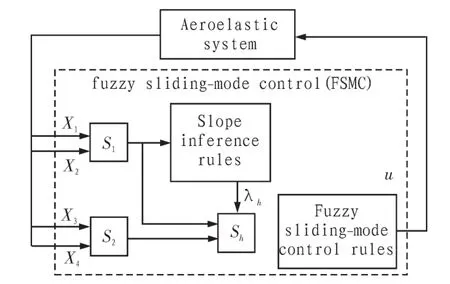
圖2 模糊滑模控制系統框圖Fig.2 Block diagram of fuzzy sliding mode control system
斜率推理規則表示為:
模糊滑模控制規則表示為:
規則 j:如果sh是,那么 u是 Ωj
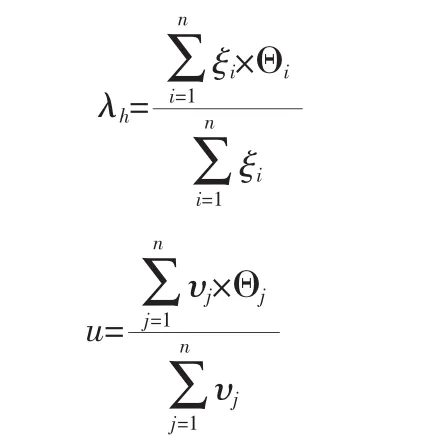
3 仿真結果
FSMC的推導并不需要使用氣動彈性系統模型。FSMC的設計是基于假設所有的狀態(h,˙)是可用的。 為了調查FSMC 的有效性,我們提供一個不穩定的狀態[h(0)=0.01,0,α(0)=0.1,=0]。
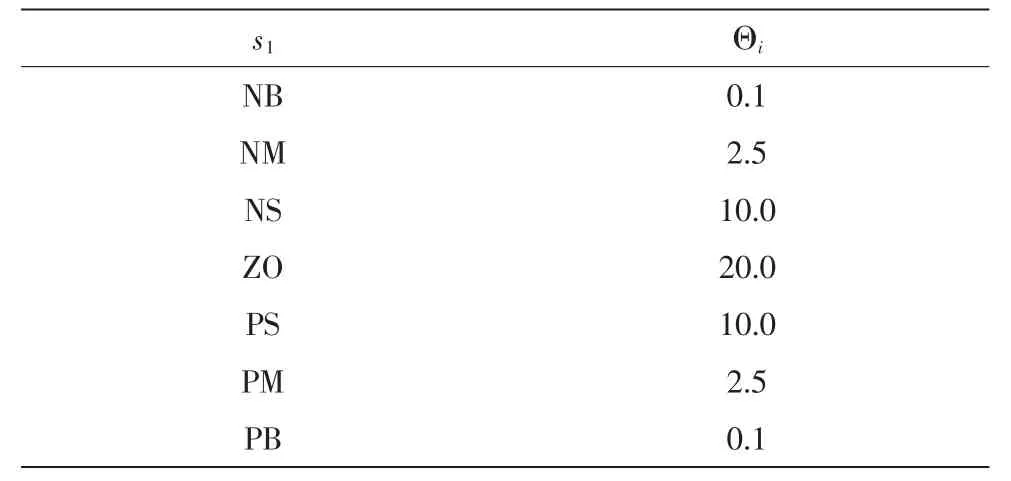
表1 滑模面斜率推理規則Tab.1 Fuzzy rules for the slope of the sliding surface
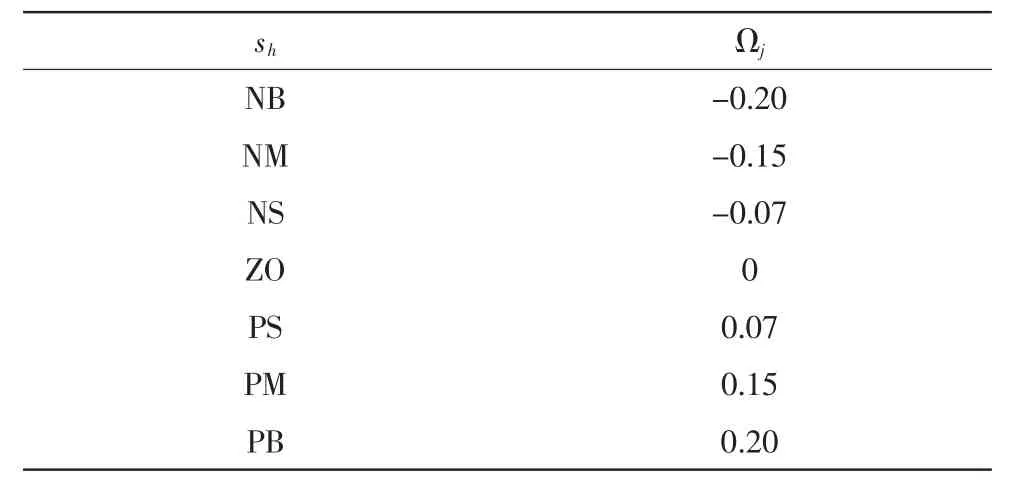
表2 模糊滑模控制推理規則Tab.2 Fuzzy rules for the fuzzy sliding mode control action
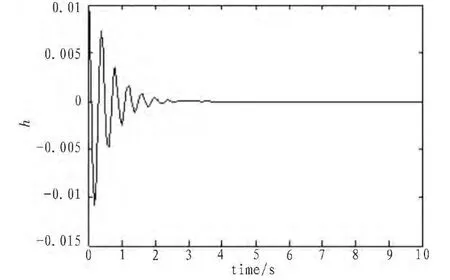
圖3 使用FSMC的系統響應hFig.3 Plunge,system responses using FSMC
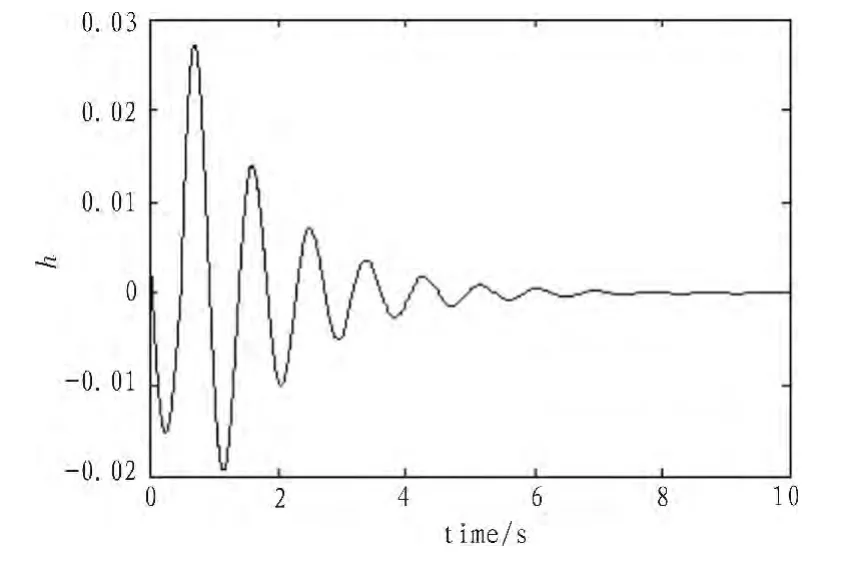
圖4 使用ADC的系統響應hFig.4 Plunge,system responses using ADC
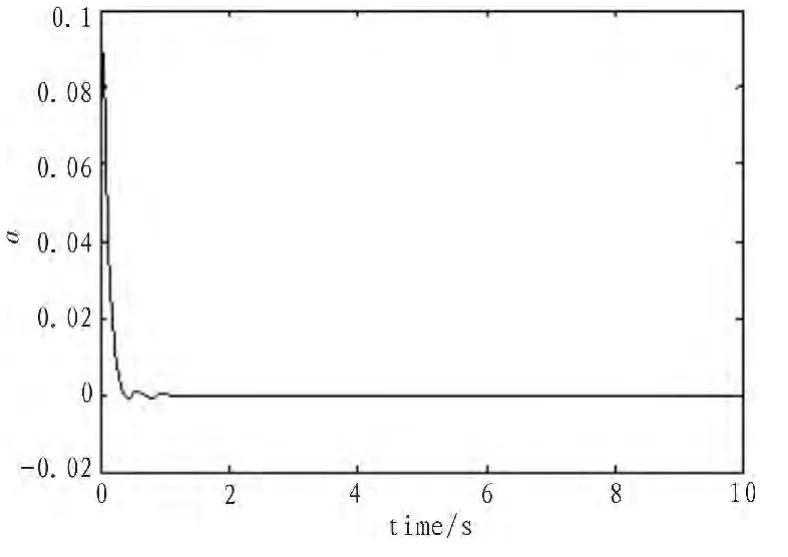
圖5 使用ADC的系統響應俯仰角Fig.5 Pitch,system responses using ADC
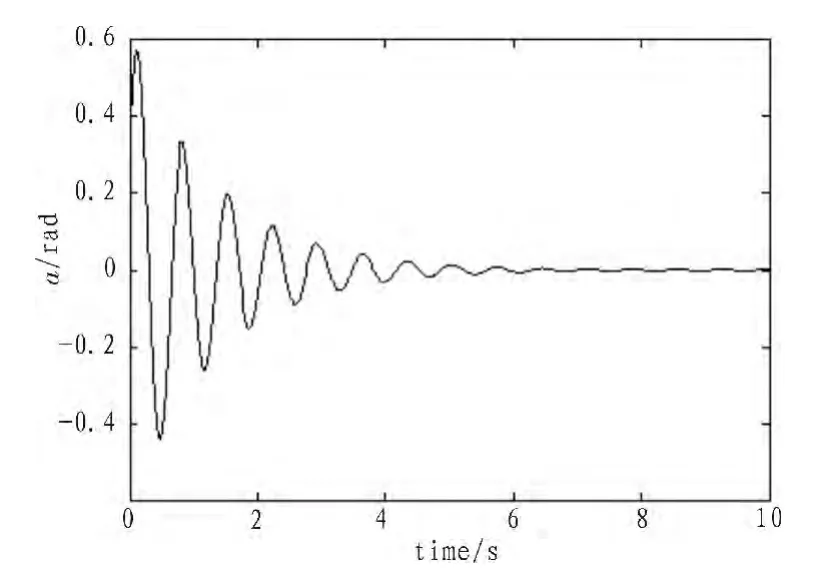
圖6 使用FSMC的系統響應俯仰角Fig.6 Pitch,system responses using FSMC
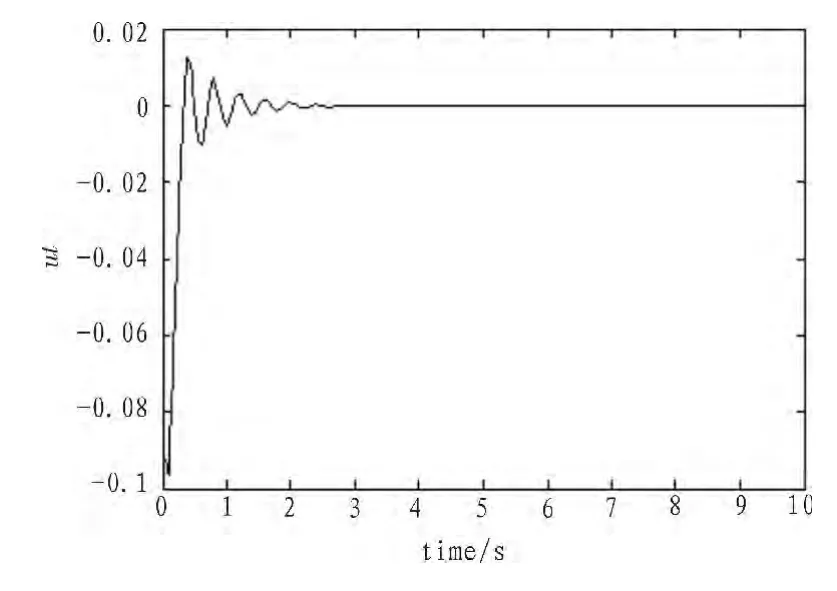
圖7 使用FSMC的輸入量utFig.7 Input using FSMC
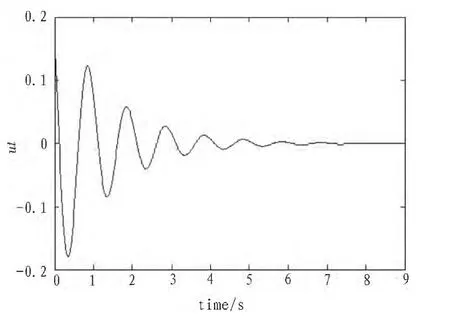
圖8 使用ADC的輸入量utFig.8 Input using ADC
使用FSMC和自適應控制(ADC)的仿真結果在圖3~8中顯示。可見,FSMC算法的優勢在于超調量很小,調整時間小,收斂性快。
4 結 論
文中提出一種模糊滑模控制方法,分析了非線性氣彈機翼的顫振,設計了一種模糊滑模控制器,用來抑制顫振。滑模控制用來使系統漸近穩定于原點,結合模糊控制用來消除滑模控制的抖振特性,保持系統的穩定性。仿真展示了模糊滑模控制和自適應控制分別應用于一個不穩定的狀態,結果顯示在抑制非線性機翼顫振的方面,模糊滑模控制具有更好的控制特性。
[1]ZHANG Jian,XIANG Jin-wu.Nonlinear aeroelastic response of high-aspect-ratio flexible wings[J].Chinese Journal of Aeronautics,2009(4):355-363.
[2]司益坡.柔性機翼顫振主動抑制研究[D].南京:南京航空航天大學,2012.
[3]Keum W Lee,Sahjendra N Singh.Adaptive control of a nonlinear aeroelastic system despite gust load[J].Journal of Vibration and Control,2013,19 (12):1807-1821.
[4]Singh Sn,BRENNER M.Limit cycle oscillation and orbital stability in aeroelastic systems with torsional nonlinearity[J].Nonlinear Dynamics,2003(31):435-450.
[5]Price S J,Lee B H K,Alihanbari H.An analysisofthe post-instability behaviour of a two-dimensional airfoil with a structural nonlinearity[J].Journal of Aircraft,1994,31(6):1395-1401.
[6]XIE Chang-chuan,YANG Chao.Linearization method of nonlinear aeroelastic stability for complete aircraft with highaspect-ratio wings[J].Science China Technological Sciences,2011(2):403-411.

