波發生器作用下柔輪變形機理的非線性有限元分析*
郭 剛,鐘 健
(深圳職業技術學院機電工程學院,廣東深圳 518055)
0 引言
諧波齒輪傳動技術是近年來發展起來的一種傳動技術,其特點是用柔性元件所產生的可控波動變形實現動力的傳遞。與傳統傳動機構相比有許多獨特的優點比如:運動精度高、回差小、體積小、承載能力高、傳動精度和傳動效率高等,目前已應用于眾多領域中。在當前使用諧波齒輪傳動中,應用最為廣泛的幾種波發生器均是剛性的。為了實現柔輪與波發生器的輪齒間無側隙嚙合,近幾年一些專家學者提出了彈性波發生器的概念[1],這種波發生器的優點在于通過調整波發生器變形力可改變柔輪徑向變形量,從而實現上述目的。
若要實現無側隙嚙合,需研究柔輪的變形與波發生器變形力間的關系,及相應的柔輪的形變、應力和應變分布規律,以利用其指導諧波齒輪的設計。為此筆者利用MSC.Patran建立了分析諧波齒輪傳動柔輪變形的非線性接觸有限元計算模型,詳細的分析柔輪在彈性波發生器接觸作用下的變形過程和機理。
1 有限元模型
根據常用的雙諧波齒輪實際情況,在MSC.Patran中建立了分析模型,并詳細的分析了波發生器與柔輪間的相互作用。其中接觸狀況按非線性處理。
1.1 3D模型的建立與有限元網格劃分
按照典型雙諧波齒輪機型的參數進行模型的建立。柔輪所選用的材料的牌號為30CrMnSiA,其彈性模量為206 GPa,泊松比取0.3。柔輪實際尺寸及柔輪輪齒部分相關參數如圖1所示。
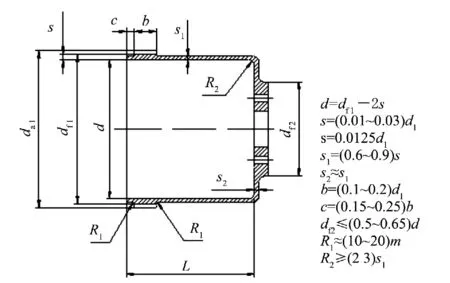
圖1 杯形柔輪結構簡圖和尺寸
建模時為了減少網格劃分和計算所用機時,忽略了柔輪底凸緣根部及齒輪根部小圓角,其原因在于文中研究波發生器作用下的柔輪變形,距離該圓角所在位置較遠,忽略圓角對計算結果影響非常小。同樣柔輪輪齒部分數量多和相對尺寸較小,劃分有限元網格時,會造成相對較多的單元數量及增加網格劃分的難度,而筆者主要研究柔輪在彈性波發生器作用下的預變形,因此在不影響計算精度的情況下將柔輪輪齒簡化為等效厚度的齒圈。
同時,為了進一步減少計算的機時,利用模型的對稱性,針對半個柔輪進行計算。網格劃分使用八節點六面體實體單元,網格劃分后得到約47 000個網格單元。根據實際變形中波發生器相對剛度大,變形很小的特點,將波發生器的作用由一個與波發生器輪廓線和軸向長度相同的剛性圓柱面代替。有限元計算模型如圖2所示。

圖2 杯形柔輪模型
1.2 施加約束和載荷
位移邊界條件:文中研究波發生器作用下的柔輪變形,變形主要發生在柔輪頂部開口端附近。根據實際情況和計算要求限制柔輪底部凸緣表面全部6個自由度,由于利用零件的對稱的特點,只計算一半的零件。計算時設定在對稱面處周向位移為0。
接觸邊界:在 MSC.Patran/Marc中設定接觸邊界,將柔輪設定為變形體,波發生器設定為運動剛體同時給定其徑向運動規律。波發生器沿徑向向外運動,與柔輪內側接觸,并使柔輪逐漸發生形變。在設定邊界條件時給定其位移增量。根據問題的具體情況,計算時忽略兩物體間摩擦力。
2 結果和分析
2.1 杯形柔輪位移分布
圖3為杯形柔輪計算結果沿剛體運動方向的位移分布圖。

圖3 杯形柔輪計算結果的位移分布
變形云圖顯示柔輪的位移變形以波發生器接觸的相關區域為界對稱分布。杯形柔輪的變形量的量值由開口端向封閉端逐漸減小。波發生器的最大位移是0.39 mm。圖3中可看出在波發生器作用下,杯形柔輪的最大位移為0.426 mm,發生在其與波發生器接觸的相關區域靠近開口端一側。表明柔輪產生了輕微翹曲。同時最大變形區域已與運動剛體柱面已脫離接觸。而封閉端的變形最小,幾乎接近零。
2.2 杯形柔輪位移與變形力
圖4為柔輪變形與變形力有限元計算結果曲線。研究圖4所給出示的結果曲線可得出,柔輪變形量與變形力存在基本上呈線性關系。
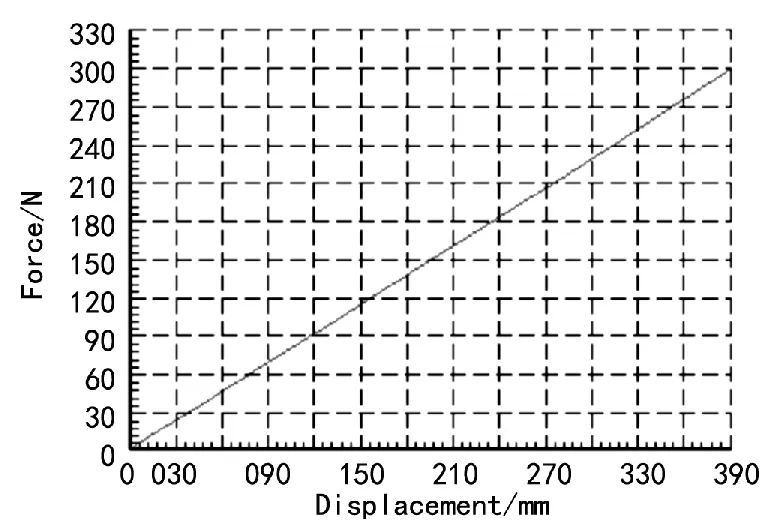
圖4 柔輪變形與變形力有限元計算結果曲線
2.3 杯形柔輪的應變分布
圖5 為柔輪等效應變分布圖。由圖5可見柔輪的應變沿水平和鉛垂方向呈對稱分布,其最大等效應變發生在波發生器與柔輪相接觸區域。同時,對該區域的等效應變分布進一步分析知:柔輪與波發生器接觸區域開口一側發生了翹曲,柔輪最大等效應變出現在柔輪與波發生器相接觸區域內遠離柔輪開口端處。

圖5 柔輪等效應變分布圖
圖6 ~8分別為柔輪水平、垂直和軸向方向應變分布圖。其同樣沿水平和鉛垂方向呈對稱分布。柔輪水平方向應變最大值出現在對稱面處齒輪圈外緣。柔輪垂直方向和軸向應變最大值出現在波發生器與柔輪接觸區域遠離柔輪開口端處。
2.4 杯形柔輪的應力分布
圖9為柔輪Von Mises應力分布圖。由圖9可見柔輪的應力沿水平和鉛垂方向與應變一樣同樣呈對稱分布,其最大Von Mises應力發生在波發生器與柔輪接觸區域。最大Von Mises應力出現在柔輪與波發生器相接觸區域遠離柔輪開口端的區域,與最大等效應變位置相對應。

圖6 柔輪水平方向應變分布圖

圖7 柔輪垂直方向應變分布圖
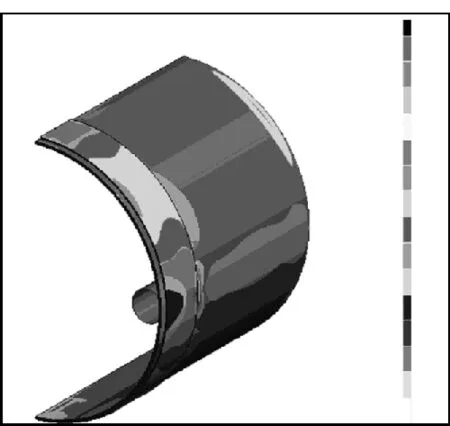
圖8 柔輪軸向應變分布圖
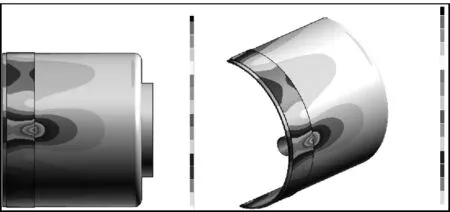
圖9 柔輪Von Mises應力分布圖
圖10 ~12分別為柔輪水平、垂直和軸向方向應力分布圖。其同樣沿水平和鉛垂方向呈對稱分布。相應的最大值與對應的應變分布相對應。
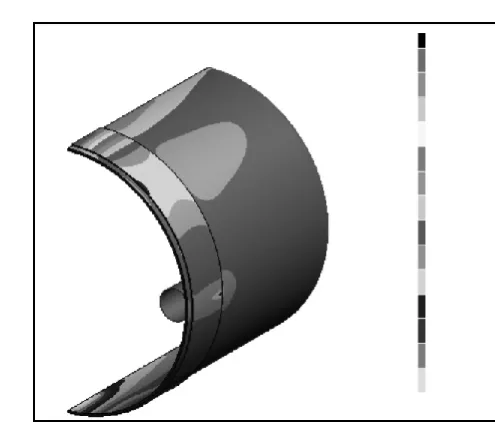
圖10 柔輪水平方向應力分布圖
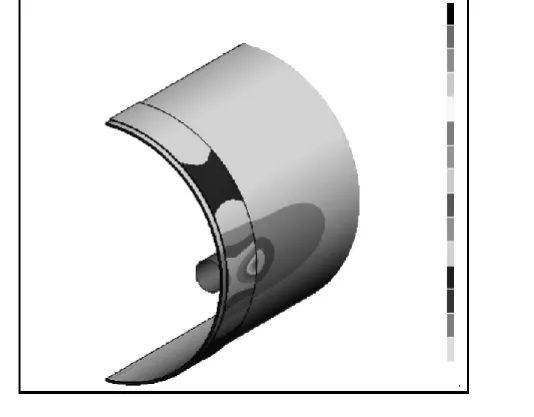
圖11 柔輪垂直方向應力分布圖

圖12 柔輪軸向應力分布圖
3 結語
利用MSC.Patran建立了諧波齒輪傳動柔輪變形的非線性接觸有限元計算模型,通過分析柔輪在彈性波發生器接觸作用下的變形過程,得到較準確的柔輪徑向變形量與徑向變形力的關系規律。由分析結果可知,柔輪初始變形力與柔輪形變基本成線性關系。
通過分析了諧波齒輪傳動柔輪的形變給出了其在波發生器作用下的位移、應變和應力的分布規律。分布為對稱分布,各項最大值均出現在接觸區域。
[1] 辛洪兵.一種在諧波傳動中使柔輪與波發生器緊密接觸的方法及浮動式波發生器[P].中國專利1032010334.
[2] 李秋芳,鐘 健,程 凱.諧波齒輪傳動柔輪變形與變形力研究[J].機械設計,2008(11):48-50.

