遞推SOM神經網絡在短時交通流預測中的應用

黃 杰 李 軍 郭 翔

(蘭州交通大學自動化與電氣工程學院1，甘肅 蘭州 730070;青藏鐵路公司2，青海 西寧 810000)

遞推SOM神經網絡在短時交通流預測中的應用

黃 杰1李 軍1郭 翔2

(蘭州交通大學自動化與電氣工程學院1，甘肅 蘭州 730070;青藏鐵路公司2，青海 西寧 810000)

針對短時交通流預測，提出遞歸自組織映射(SOM)神經網絡方法。根據SOM神經網絡的聯想記憶技術，分別給出考慮了反饋的RecSOM模型和能夠利用結構化信息的SOMSD模型。遞推SOM方法用全SOM作為重復神經元，用歷史活動與當前信息的組合作為輸入，通過訓練神經元的權值及上下文信息學習時序動態。將遞推SOM方法應用于預測某地區實測交通流數據，并與現有方法進行比較。試驗結果表明,遞推SOM方法能有效改善預測精度，在同等情況下優于其他方法。

短時交通流 智能交通 自組織映射 神經網絡 遞推 預測

0 引言

目前，智能交通系統(intelligent transportation systems,ITS)已有長足發展，但擁塞控制等問題仍難以解決，預測交通流有助于相關部門或者個人掌握交通趨勢，選擇最佳出行路徑。先進交通控制系統(advanced traffic management systems,ATMS)也可根據預測值采取前瞻性措施，計劃交通路線的最佳組合，實現擁堵控制。

在交通流預測領域，為了有效表達交通流量的不確定性和時變性，機器學習方法已成為主流預測手段。文獻[1]采用小波神經網絡實時預測交通流，文獻[2]采用非參數回歸算法預測短時交通流。文獻[3]采用最小最大概率回歸機(minimax probability machine regression,MPMR)網絡實現短時交通流預測。文獻[4]采用監督的在線加權學習算法預測短時交通流，均取得了較好的預測效果。可以看到，關于短時交通流預測的研究大部分采用監督學習神經網絡。但在實際應用中，由于監督信息常常無法或者很難獲得，因此發展非監督模型日趨重要；且由于交通流數據量一般較大，因此可處理結構化信息的網絡更受青睞。

1 遞推SOM預測方法

完全非監督自組織映射(self-organizing map,SOM) 神經網絡[5-6]是芬蘭Teuvo Kohonen教授提出的一種完全非監督競爭學習型神經網絡。其構造簡單直觀、拓撲保持能力、輸出可視化等優點已在機器學習領域引起關注。另外，SOM拓撲保持的全局性也避免了許多神經網絡方法容易陷入局部最優的問題。

基于SOM神經網絡的拓撲保持映射的能力，將SOM神經算法與遞推思想相結合，所構建的遞推SOM預測方法能進一步提高預測精度，包括RecSOM(recursive self-organizing map)和SOMSD(SOM for structured data)兩種預測模型。這兩種預測模型的區別在于對上下文向量(context vector)的表示不同。RecSOM模型用帶時延的反饋表現遞推的概念，SOMSD模型利用獲勝神經元的網格坐標表示上下文信息，更適用于結構化數據。

將遞推SOM方法應用于短時交通流預測實例中，在同等條件下，與現有的反向傳播(BP)神經網絡、支持向量機(SVM)等方法的預測結果進行比較，以驗證所提出方法的有效性。

相對于SOM僅依據當前輸入實現預測，遞推SOM方法不僅考慮當前輸入，也考慮歷史信息。根據SOM的聯想記憶技術，遞推SOM方法用歷史活動與當前信息的組合作為網絡輸入，存儲了輸入向量在大小、方向上的變化，一定程度上彌補了用窗函數方法處理數據時連續向量之間上下文信息的丟失。

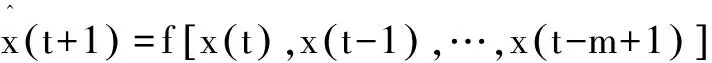
(1)

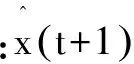
利用SOM網絡逼近具有輸入-輸出特性的非線性映射，網絡的輸入向量x(t)∈G定義為兩部分，包括模型輸入xin(t)和預測輸出xout(t)：

(2)

(3)

定義SOM輸出平面的狀態表示為y(t)∈G，則輸出平面狀態的不斷變化呈現為相繼的y(t)。為了保證歷史活動的影響力，遞推SOM方法的訓練算法中對獲勝神經元的選擇考慮了上下文的影響。

令y=[y(t)…y(t-p)]，p為任意長度。當前輸入x(t)對應的輸出y(t)的上下文為yold=[y(t-1)…y(t-p)]。

將神經元i的權值向量表示為wi，遞推SOM的廣義輸入包括xin(t)和對上下文yold的表示兩部分，SOM平面上的每個神經元i的權值對應有wix與wiy兩部分：

(4)

wix劃分為wiin和wiout兩部分，其中wiin為網絡輸入xin對應的權值；wiout為預測輸出xout對應的權值。

令i*(t)表示獲勝神經元，SOM用歐式距離最小來確定網絡輸入與權值wiin的最優匹配：

(5)

式中：d=‖xin(t)-wiin(t)‖為歐氏距離；t為與算法迭代響應的離散時間步。

遞推SOM方法考慮了上下文yold，而調整距離函數改稱為遞推距離drecursive，以示與SOM區別。遞推SOM方法按遞推距離最小確定獲勝神經元[7]：

(6)

上下文信息yold影響了獲勝神經元的確定，被視為表現了獲勝神經元間的轉移。當y(t)對應的上下文yold與前一時間步的獲勝神經元的坐標相似時，則該神經元更可能獲勝。

特別地，遞推SOM用全SOM作為重復神經元來表現上下文信息，方法的距離計算不僅考慮單個神經元的上下文信息，而且考慮整個映射平面的歷史活動。這種表現遞推的形式是自我參照的，體現了對自身活動的歸類。

為了計算距離，針對上下文信息yold，令序列的上下文表示(contextrepresentation)為C(yold)。雖然RecSOM模型與SOMSD模型的C(yold)不同，但遞推距離函數可統一表示為：

(7)式中：wiy為上下文所對應的權值；α與β為標量參數。

RecSOM模型與SOMSD模型的上下文表示C(yold)分別為CRecSOM(yold)與CSOMSD(yold)。由于上下文信息影響了對輸入權值xin和上下文表示C(yold)的訓練與更新，遞推SOM方法使相似的輸入選擇了鄰近的獲勝神經元。

RecSOM模型用時延反饋表現遞推概念，上下文表示存儲了前一時間步的所有距離值，是一個|n|維向量：

(8)

式中：|n|為映射平面的神經元數目。

任意時間步的上下文表示都需要遞推計算映射中每個神經元的遞推距離，導致了非常復雜的獲勝神經元選擇機制。

SOMSD模型利用信息壓縮處理結構化數據，是歷史活動的低維表示，用前一時間步的獲勝神經元的網格坐標gi*表示上下文信息：

(9)

遞推SOM網絡訓練完成后，預測輸出值為wiout(t)，即對應xout(t)的權值部分：

(10)

1.1 RecSOM模型

為了改進預測精度，文獻[9]給出了一種用時延反饋來表現遞推概念的策略，與SOM算法結合得到RecSOM模型。模型在保持SOM全部特性的基礎上采用遞推連接，且遞推連接與前向連接均等，考慮了交通流量數據的時序性。通過合并當前輸入和歷史活動來表示時間的方法是自我參照的，體現了映射對自身行為的學習歸類以及對數據歷史活動的理解。

RecSOM模型是SOM算法在當前輸入x(t)與前一時間步狀態y(t-1)上的迭代表示，如圖1所示。圖1中，虛線表示可訓練的連接，連續的箭頭表示固定的一對一連接；黑色圓圈表示SOM在t時刻計算得出的獲勝神經元，灰色圓圈表示在(t-1)時刻的獲勝神經元，白色圓圈表示神經元，構成SOM神經網絡的輸出拓撲。具體方法是將當前輸入與SOM輸出平面之前的狀態聯系起來，共同作為網絡輸入，學習交通流量信息中隱含的規律。因此，每個神經元響應一系列輸入。

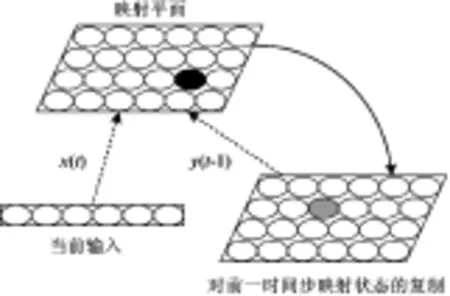
圖1 RecSOM的拓撲結構

將當前輸入x(t)和上下文yold|p=1=y(t-1)共同作為對傳統SOM算法的輸入，映射單元需要學習一對數據(輸入，上下文)的表示。

模型通過計算遞推距離最小確定獲勝神經元。分別計算映射神經元i的權值向量wiin和wiy與網絡輸入xin(t)和上下文向量y(t-1)的歐氏距離，其中，wiin為wix中網絡輸入xin對應的權值。按照前向連接與反饋連接是均等的，構建遞推距離為：

(11)

前向權值和遞推權值同時更新：

(12)

(13)

拓撲領域用高斯表示，完成量化：

(14)

為了保證權值向量收斂到穩定狀態，學習率η(t)與鄰域函數有效寬度σ(t)>0隨時間的增加而逐漸衰減，可選用指數衰減的形式，如下：

(15)

(16)

式中：η0與ηT分別為學習率η(t)的初值與終值；σ0與σT分別為鄰域函數有效寬度σ(t)的初值與終值；T為算法訓練的迭代次數。

由于RecSOM模型加入了反饋，因此需要考慮網絡在學習過程中的穩定性，權值的期望值需在學習過程中收斂。神經元i的上下文yi表示為：

(17)

由于反饋連接的轉換函數決定了RecSOM模型的穩定性，依據經驗選擇轉換函數如下：

(18)

轉換函數連續且取值在0到1之間。針對匹配單元，函數值接近于1，高斯拓撲形式保證在輸入、權值或者歷史活動中的擾動都不影響匹配單元的穩定性。針對不匹配單元，函數值接近于0，因此，無論處于何種狀態，模型始終穩定。

1.2 SOMSD模型

許多自然或人工系統利用數據結構實現更精確地建模，數據的結構化表示包含更大的信息量。為了處理編碼為標記的有向無環圖(directed acyclic graphs,DAGs)的結構化信息，Markus Hagenbuchne[10]等人提出SOMSD方法以處理結構化數據。該方法在完成結構化目標向拓撲平面映射的同時能找到輸入間的相似性，遞推學習過程加強了對模式分類的識別能力。在輸入結構的拓撲映射中，神經元的空間位置表現了結構的統計特征。

針對短時交通流預測構建SOMSD模型，主要的創新點在于將獲勝神經元的坐標作為下一時間步的上下文信息，且將上下文信息視為SOM的標準輸入。也就是說，預測模型利用SOM的數據壓縮能力采用前一時間步的獲勝神經元的網格坐標gi*表示上下文信息。利用SOM的拓撲保持特性訓練神經元權值及上下文信息，在相似性標準下聚類數據，即可誘導出模型對輸入空間的度量。

SOMSD模型的遞推距離函數為：

(19)

SOMSD模型中，權值wix的更新與RecSOM模型相同，見式(12)。類似地，上下文對應的權值wiy的更新為：

(20)

式中：gold=CSOMSD(yold)為之前時間步的獲勝神經元的網格坐標。

相對于RecSOM模型需要設定反饋的轉換函數這樣較為復雜的獲勝神經元選擇機制，SOMSD模型用網格坐標gi*表示上下文的信息壓縮手段確保了更快的處理速度。由于模型中的上下文信息是對歷史活動的低維表示，因此SOMSD模型是降低復雜度的壓縮模型。雖然壓縮效果有效降低了模型運行時間，但SOMSD在實例中的預測精度與RecSOM持平。

針對樹狀結構數據研發的SOMSD方法，可將標號轉化為一系列固定大小的向量。模型嘗試在輸入數據的權值及上下文向量中識別隱存的規律，映射平面通過返回獲勝神經元的坐標表示對信息的壓縮描述，如圖2所示。

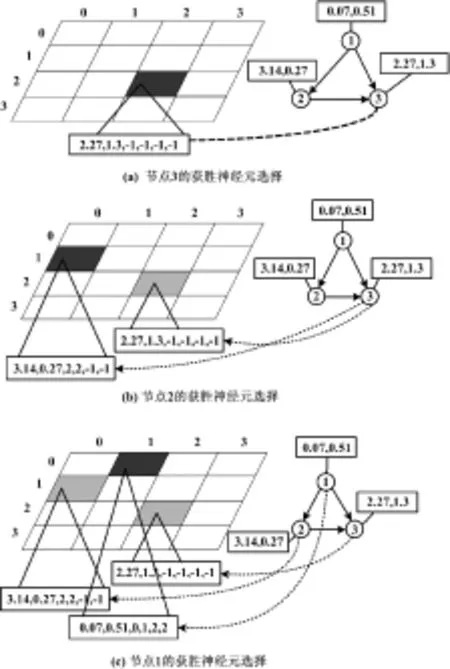
圖2 對輸入的遞推映射舉例

圖2中，黑色區域表示在t時刻的獲勝神經元，灰色區域表示在(t-1)或(t-2)時刻的獲勝神經元。在圖2(a)中，節點3數據輸入映射平面,獲勝神經元坐標為(2,2)。用此信息來表示節點2的輸入向量，得到獲勝神經元坐標為(0,1)，如圖2(b)所示；最后將全部信息輸入映射平面，獲勝神經元坐標為(1,0)，如圖2(c)所示。

1.3 算法描述

1) 數據預處理與網絡初始化。

① 將數據劃分為訓練集與測試集，確定輸入的維數，構建網絡的輸入輸出。

② 初步確定網絡的神經元拓撲，分別初始化權值wix和wiy，以及上下文向量C(yold)。

2) 網絡的迭代訓練。

① 順序代入輸入向量，利用權值向量wiin和wiy計算遞推距離函數drecursive并確定獲勝神經元i*(t)，其中t為時間步。

② 利用RecSOM的反饋連接轉換函數或SOMSD的信息壓縮手段計算上下文向量C(y)。

③ 通過計算映射平面其他神經元與獲勝神經元的距離，分別更新權值向量wix和wiy。

④ 迭代直至輸入數據按順序代入完畢，網絡訓練結束，得到預測輸出為wiout(t)，即xout(t)對應的權值部分。

3) 調整模型參數，直至預測精度達到最優，算法結束。

2 交通流預測實例分析

將遞推SOM方法用于交通流預測實例，采用相空間重構方法處理數據，用互信息法確定時間延遲，用CAO方法確定嵌入維數。

作為對預測方法整體表現的衡量，選用均方誤差(meansquareerror,MSE) 、正則化均方誤差(normalizedmeansquareerror,NMSE)兩種評估標準：

(21)

(22)

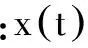
2.1 預測模型參量的選取

為了完成對數據分布的探索，SOM神經網絡的神經元數目一般較大。如果神經元數目過少，部分聚類結果會因為異常值的存在而不精確，但若神經元數目偏多，則總有一部分神經元始終不被選中，導致神經元利用率偏低。不過，正是網絡中沒有用到的這些神經元提高了模型的泛化能力。試驗結果顯示，神經元利用率與數據集大小成反比，當SOM網絡的神經元數目選為數據集大小的三分之一時，網絡的學習效果最佳。

SOM算法要求領域半徑初始值取得較大，以降低陷入局部極小的可能，而試驗顯示在一段范圍內，遞推SOM模型的鄰域半徑初值取得較小時預測效果更好。因為遞推SOM模型依據節點類型聚類輸入數據，聚類結構在訓練初期就已經建立，之后聚類位置僅有微小改變，且主要更新發生在聚類內部。鄰域函數半徑取較小值，可使網絡訓練集中在較小的區域內；半徑取較大值時表現出干擾的效果。

最后，針對網絡迭代次數的問題，遞推SOM網絡的預測精度表現為隨迭代次數的增加穩定上升，但超過一定閾值后就開始下降，反映了網絡泛化能力會由于“過擬合”效應而降低。

2.2 實例一

實例一選取了英國某地區交通局的交通數據，觀測時間為2011年3月,時間段為6∶00～20∶00，時間間隔取15min。本例中截選了交通流量序列的336個時間點。時間延遲τ=2，嵌入維數m=3。遞推SOM神經元結構為15×15，σ=16，α=323，β=1，η=0.5。

實例一不同方法預測結果比較如表1所示，圖3為在數據集上SVM、SOM、遞推SOM模型預測值與實際值的對比。

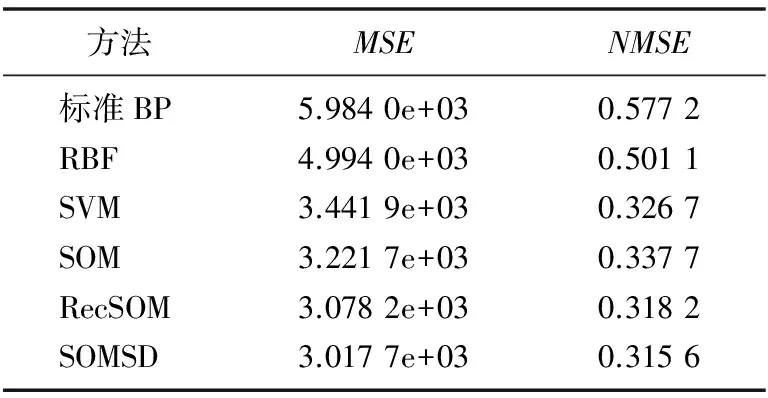
表1 實例一不同方法預測結果比較

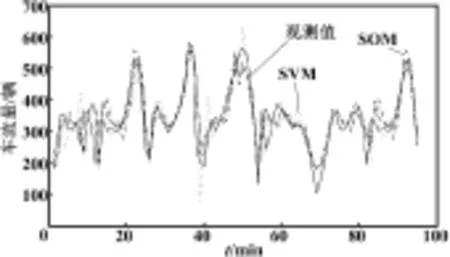
圖3 實例一交通流量預測曲線

2.3 實例二

實例二的數據集來源于西雅圖華盛頓大學ITS研究組的交通數據采集與分布(traffic data acquisition and distribution,TDAD)數據庫，其網絡站點為：www.its.washington.edu/tdad/，站點提供西雅圖地區探測器所記錄的交通流量值。本例選擇探測器ES-088D記錄的數據[11]，采集數據的時間為2005年6月6日至7月3日，時間間隔取為15 min，將交通流量數據處理為序列，共2 688個數據點。時間延遲τ=1，嵌入維數m=10。遞推SOM方法的神經元結構為25×25，σ=60，α=323，β=1，η=0.5。

實例二不同方法預測結果比較如表2所示，圖4為在數據集上SVM、SOM、RecSOM、SOMSD方法的預測值與實際值的對比。

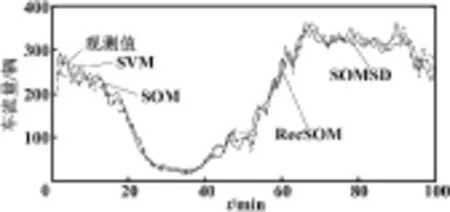
圖4 實例二交通流量預測

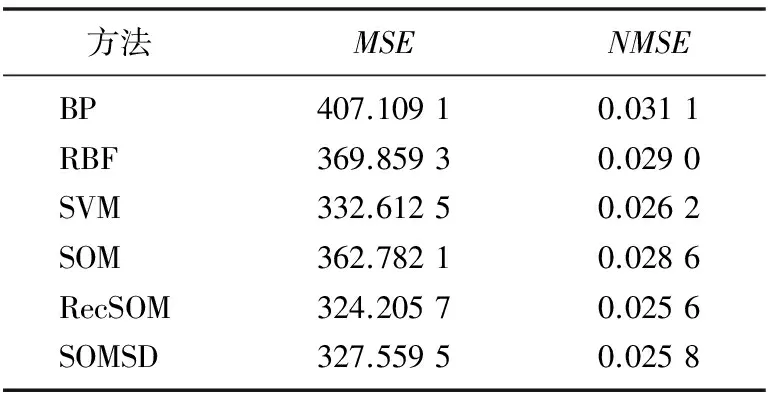
方法MSENMSE BP407．10910．0311 RBF369．85930．0290 SVM332．61250．0262 SOM362．78210．0286 RecSOM324．20570．0256 SOMSD327．55950．0258

由表1、表2所示，在相同條件下，采用本文方法與BP神經網絡方法、RBF神經網絡方法、SVM方法構建的預測模型比較結果可以看出，遞推SOM預測方法精度最高。由圖3、圖4所示交通流量預測曲線可以看出，遞推SOM方法的預測曲線與實際曲線的重合度較高，取得了滿意的預測效果。

3 結束語

針對短時交通流預測，本文提出遞推SOM方法，包括RecSOM模型和SOMSD模型。該方法不僅考慮當前輸入，也能實現對歷史事件的記憶最大化。RecSOM模型用帶時延的反饋表現遞推的概念，SOMSD模型利用獲勝神經元的網格坐標表示上下文信息，更適用于結構化數據。上下文信息不僅包含了數據集的拓撲統計特性，還體現了網絡自身的變化規律。將遞推SOM方法的預測模型應用于兩個交通流實例，并在同等情況下與其他預測方法進行對比，結果驗證了方法是可行的、有效的。

[1] Li R H,Xu J M,Luo Q,et al.Real-time traffic flow forecasting based on wavelet neural network[J].International Journal of Online Engineering(iJOE),2013,9(3):72-76.

[2] 梁秀霞,胡姍姍,李偉斌.非參數回歸算法在短時交通流預測中的應用[J].自動化儀表,2011,33(4):21-23.

[3] 王嬌.最小最大概率回歸機在短時交通流預測中的應用[J].公路交通科技,2014,31(2):121-127.

[4] Jeong Y S,Byon Y J,Castro-Neto M M,et al.Supervised weighting-online learning algorithm for short-term traffic flow prediction[J].IEEE Transactions on Intelligent Transportation Systems,2013,14(4):1700-1707.

[5] Haykin S S.Neural networks and learning machines[M].New York:Prentice Hall,2009.

[6] Barreto G A.Time series prediction with the self-organizing map:a review[J].Perspectives of Neural-symbolic Integration,Studies in Computational Intelligence,2007,77:135-158.

[7] Hammer B,Micheli A,Sperduti A,et al.A general framework for unsupervised processing of structured data[J].Neuro Computing,2004,57:3-35.

[8] Blohm S.Data mining on sequences with recursive self-organizing maps[D].Bachelor thesis,University of Osnabrück,2003.

[9] Voegtlin T.Recursive self-organizing maps[J].Neural Networks,2002,15(8):979-991.

[10]Hagenbuchner M,Sperduti A,Tsoi A C.A self-organizing map for adaptive processing of structured data[J].IEEE Transactions on Neural Networks,2003,14(3):491-505.

[11]Xie Y,Zhao K,Sun Y,et al.Gaussian processes for short-term traffic volume forecasting[J].Transportation Research Record:Journal of the Transportation Research Board,2010,2165:69-78.

Application of the Recursive SOM Neural Network in Short-term Traffic Flow Prediction

For short-term traffic flow prediction, the method of recursive self-organizing map (SOM) neural network is proposed. On the basis of the associative memory technology of SOM neural network, the ResSOM model considering feedback and the SOMSD model capable using structured information are given respectively. The method of recursive SOM uses full SOM as the replicated neuron, and the combination of historical activities and current information as the input; it learns time series dynamics by training the weight value of neuron and context information. The method of recursive SOM is applied in prediction of measured traffic flow data of an area, and comparison with existing method is conducted, the experimental results show that the method of recursive SOM effectively improves the prediction accuracy; it is superior to other methods under the same circumstances.

Short-term traffic flow Intelligent transportation Self-organizing map Neural network Recursion Prediction

國家自然科學基金資助項目(編號：51467008)；

黃杰(1990-)，女，現為蘭州交通大學交通信息工程及控制專業在讀碩士研究生；主要從事自組織映射網絡在時間序列預測方面的研究。

TP391

A

10.16086/j.cnki.issn1000-0380.201504001

甘肅省高等學校基本科研業務費專項資金項目(編號：620026)。

修改稿收到日期：2014-11-25。