淺談利用變式進行運動型問題的復(fù)習(xí)

高云芳

摘 要 運動型問題常常與探究性問題、分類討論問題結(jié)合在一起，學(xué)生在解答此類問題時普遍感到困難，若設(shè)計變式題組進行運動型問題復(fù)習(xí)，由易到難、循序漸進，有利于提高學(xué)生對運動型問題的分析、解決能力。

關(guān)鍵詞 探究 運動型 問題 變式 能力

中圖分類號：G633.6 文獻標(biāo)識碼：A 文章編號：1002-7661（2015）11-0041-03

一、利用習(xí)題變式，培養(yǎng)學(xué)生探究運動型問題的意識

在運動型復(fù)習(xí)的教學(xué)中，把問題由靜態(tài)情景變?yōu)閯討B(tài)情景，由特殊位置到一般情形，變解題模式為“探究式”。 變式題可滿足學(xué)生的好奇心，培養(yǎng)學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣，使學(xué)生掌握運動型問題中“動靜互化”，有利于培養(yǎng)學(xué)生探究、解決運動型問題的意識。

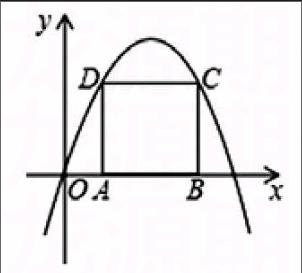
例：如圖，一條拋物線y=ax2+bx（a≠0）的頂點坐標(biāo)為（2，），正方形ABCD的邊AB落在x軸的正半軸上，頂點C、D在這條拋物線上。

（1）求這條拋物線的表達式；

（2）求正方形ABCD的邊長。

分析：（1）設(shè)拋物線頂點式解析式y(tǒng)= a（x-2）2+，

然后把原點坐標(biāo)代入計算求出a的值即可得解；故拋物線解析式為y= - x2+ x；

（2）設(shè)正方形的邊長為2m，根據(jù)拋物線的對稱性求出點C的坐標(biāo)，然后代入拋物線解析式計算解得m1=1，m2= -4（舍去），所以正方形ABCD的邊長為2m=2？=2。

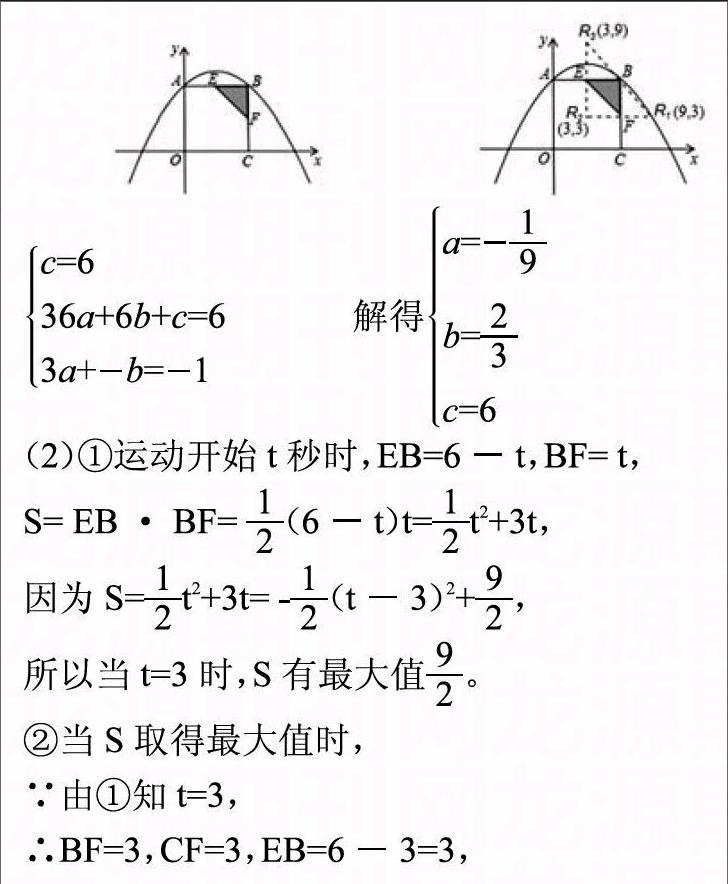
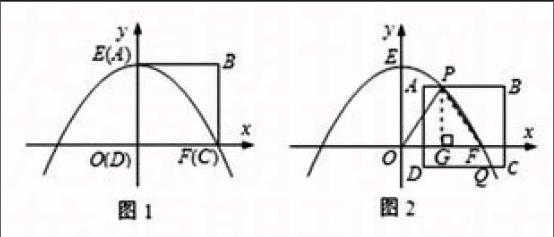
變式一 ：如圖，在直角坐標(biāo)系xOy中，正方形OCBA的頂點A，C分別在y軸，x軸上，點B坐標(biāo)為（6，6），拋物線y=ax2+bx+c經(jīng)過點A，B兩點，且3a-b=-1。

（1）求a，b，c的值；

（2）如果動點E，F(xiàn)同時分別從點A，點B出發(fā)，分別沿A→B，B→C運動，速度都是每秒1個單位長度，當(dāng)點E到達終點B時，點E，F(xiàn)隨之停止運動，設(shè)運動時間為t秒，△EBF的面積為S。

①試求出S與t之間的函數(shù)關(guān)系式，并求出S的最大值；

②當(dāng)S取得最大值時，在拋物線上是否存在點R，使得以E，B，R，F(xiàn)為頂點的四邊形是平行四邊形？……