在課堂教學(xué)中展現(xiàn)數(shù)學(xué)的特點(diǎn)和文化

蔣培杰

只見樹木不見森林，細(xì)節(jié)多、思想少，不見學(xué)科本質(zhì)，可以說是當(dāng)今中學(xué)數(shù)學(xué)課堂普遍存在的弊端。有的中學(xué)把做題當(dāng)成整個數(shù)學(xué)教學(xué)的重心，誤導(dǎo)學(xué)生周旋于難題、偏題和怪題之間，嚴(yán)重影響了學(xué)生對數(shù)學(xué)的學(xué)習(xí)興趣，并在一定程度上扼殺了學(xué)生創(chuàng)造性思維和創(chuàng)造性能力的發(fā)展。近年來，筆者嘗試在中學(xué)數(shù)學(xué)課堂教學(xué)中體現(xiàn)數(shù)學(xué)的特點(diǎn)、講述數(shù)學(xué)的文化及其與其他學(xué)科文化的相互聯(lián)系和影響，進(jìn)而滲透數(shù)學(xué)發(fā)現(xiàn)的方法論，以提高學(xué)生的學(xué)習(xí)熱情，培養(yǎng)學(xué)生的數(shù)學(xué)能力和數(shù)學(xué)素養(yǎng)，收到了良好的效果。

一、在課堂教學(xué)中展現(xiàn)數(shù)學(xué)的應(yīng)用特點(diǎn)

抽象性、精確性和應(yīng)用的極端廣泛性是數(shù)學(xué)學(xué)科有別于其他學(xué)科的三大特點(diǎn)。尤其數(shù)學(xué)應(yīng)用的極端廣泛性，最迫切、最應(yīng)該為學(xué)生在課堂中認(rèn)識到。在課堂中空泛地講“宇宙之大，粒子之微，火箭之速，日用之繁，數(shù)學(xué)無處不在”是不行的，這些是學(xué)生無法切身體驗(yàn)的。事實(shí)上，任何問題只要能用數(shù)學(xué)加以討論和解決，就會程度不同地發(fā)生實(shí)質(zhì)性的變化。我國在優(yōu)化、控制與統(tǒng)籌，設(shè)計(jì)與制造，質(zhì)量控制，預(yù)測與管理，信息處理，大型工程，資源開發(fā)與環(huán)境保護(hù)，農(nóng)業(yè)經(jīng)濟(jì)和數(shù)學(xué)物理[1]等方面都貫穿了數(shù)學(xué)的應(yīng)用思想。在課堂教學(xué)中，教師應(yīng)結(jié)合課程目標(biāo)和教學(xué)內(nèi)容，適當(dāng)?shù)亟榻B數(shù)學(xué)的應(yīng)用，培養(yǎng)學(xué)生用數(shù)學(xué)分析、解決實(shí)際問題的能力。

比如學(xué)生在課堂上學(xué)習(xí)錯位相減法有很多很好的素材，但大多與純數(shù)列相關(guān)，和實(shí)際應(yīng)用結(jié)合得較少。學(xué)生普遍認(rèn)為這個方法太繁瑣，而且沒有實(shí)際意義。事實(shí)上，這個方法是可以有一些實(shí)用性很強(qiáng)的例子的。

【例】某公司有一基建項(xiàng)目，分6個年度投資，每年末投入40 000元，預(yù)計(jì)6年后建成。若該項(xiàng)目的投資來自銀行貸款，貸款利率為10%，試問該項(xiàng)投資的投資總額是多少？[2]

教學(xué)建議：在計(jì)算這道題時，學(xué)生很有可能回答總額為40 000×6=240 000（元），這便是沒有考慮資金的時間價值。學(xué)生之所以會回答錯誤，是受了長期理想化的、與實(shí)際無關(guān)的應(yīng)用題的訓(xùn)練“熏陶”。如有必要，這時可以向?qū)W生介紹“普通年金終值”的概念，即每期期末收入或支出等額款項(xiàng)的復(fù)利終值之和。在解題的時候，我們可以設(shè)S為普通年金終值，A為每期的收付款項(xiàng)，n為記息期數(shù)，則：

S=A（1+i）0+A（1+i）1+A（1+i）2+A（1+i）3+…+A（1+i）n-3+A（1+i）n-2+A（1+i）n-1 （1）

兩邊同時乘以1+i，得：

（1+i）S=A（1+i）+A（1+i）2+A（1+i）3+A（1+i）4+…+A（1+i）n-2+A（1+i）n-1+A（1+i）n （2）

（2）-（1），得：iS=A（1+i）n-A 從而S=

本題A=40 000，n=6，i=10%，

故S==308624（元）。

顯然，這個結(jié)果與240 000元差別很大。我們這里使用的方法便是錯位相減法。課堂中也有學(xué)生直接用等比數(shù)列求和公式計(jì)算的，這當(dāng)然很好，但我們應(yīng)該讓學(xué)生明白，等比數(shù)列前n項(xiàng)和公式事實(shí)上就是由錯位相減法演變而來，如果學(xué)生還能體會到其中的類比和化歸思想那就更好了。

需要指出的是，得到本題的答案并不意味著這個案例的結(jié)束。本例的求解過程已經(jīng)建立了一個模型，即普通年金終值的計(jì)算模型：S=。以后我們可以直接利用這個模型來進(jìn)行計(jì)算。事實(shí)上，財(cái)務(wù)管理就是這么做的，財(cái)務(wù)管理里把叫做普通年金終值系數(shù)，并且就i和n的不同取值編制普通年金終值系數(shù)表，使用起來很方便。實(shí)際課堂教學(xué)中，將這些應(yīng)用呈現(xiàn)給學(xué)生，引導(dǎo)學(xué)生思考數(shù)學(xué)應(yīng)用的廣泛性，對于學(xué)生的成長是大有裨益的。

二、在課堂教學(xué)中講述數(shù)學(xué)文化及其與其他學(xué)科的相互關(guān)聯(lián)

數(shù)學(xué)與哲學(xué)、數(shù)學(xué)與藝術(shù)、數(shù)學(xué)與自然科學(xué)等等都有密切聯(lián)系[3]，它們之間互相影響、相互為用。中學(xué)數(shù)學(xué)課堂教學(xué)不能割斷這些聯(lián)系：牛頓之所以發(fā)明微積分，是他研究物理問題的需要；愛因斯坦的廣義相對論是建立在黎曼幾何的數(shù)學(xué)基礎(chǔ)上，并且其論證方法為數(shù)學(xué)中的公理化方法；伽利略用數(shù)學(xué)符號表達(dá)物理概念，并認(rèn)定宇宙之書是用數(shù)學(xué)語言寫就的；孟德爾從概率論的角度在數(shù)量上研究豌豆，發(fā)現(xiàn)了遺傳學(xué)定律；意大利數(shù)學(xué)家沃爾泰拉在一戰(zhàn)后不久創(chuàng)立了生物動力學(xué)；數(shù)學(xué)家瓊斯在扭結(jié)理論方面工作突出，并因之獲菲爾茲獎，生物學(xué)家將這一理論成果應(yīng)用到DNA分析上，對認(rèn)識DNA結(jié)構(gòu)產(chǎn)生了重大影響；數(shù)學(xué)家H.Hauptman僅用古典數(shù)學(xué)就解決了難倒現(xiàn)代化學(xué)家的晶體結(jié)構(gòu)的謎，并因之獲得諾貝爾化學(xué)獎；三角形的任意兩邊之和大于第三邊，構(gòu)成了美國三權(quán)分立的政權(quán)架構(gòu)的基礎(chǔ)；馬爾薩斯斷言人口以幾何級數(shù)增長，而生活資料以算數(shù)級數(shù)增長，聲稱戰(zhàn)爭等災(zāi)難是有益的；統(tǒng)計(jì)學(xué)家凱特勒發(fā)現(xiàn)人類幾乎所有精神和物理特征都呈正態(tài)分布；達(dá)·芬奇說欣賞他作品的人幾乎都是數(shù)學(xué)家；諾貝爾經(jīng)濟(jì)學(xué)獎得主應(yīng)用數(shù)學(xué)的程度與物理相當(dāng)，數(shù)學(xué)方法在其研究中起著相當(dāng)本質(zhì)的作用……總之，數(shù)學(xué)作為一門基礎(chǔ)學(xué)科，與其他學(xué)科有著廣泛的聯(lián)系，且相互為用。那么，如何在課堂教學(xué)中體現(xiàn)這種相互關(guān)聯(lián)呢？

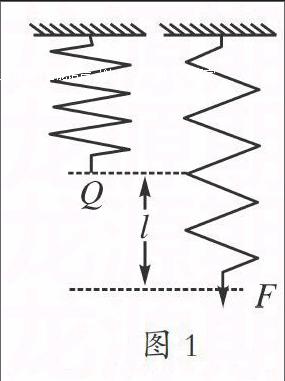
【例】如圖1，在彈性限度內(nèi)，將一彈簧從平衡位置拉到離平衡位置lm處，求克服彈力做功。

教學(xué)建議：對于彈簧變力做功問題，學(xué)生已經(jīng)記得公式W=kx2，這里要引導(dǎo)學(xué)生思考公式是怎么得到的。在彈性限度內(nèi)，拉伸（或壓縮）彈簧所需要的力F與彈簧拉伸（或壓縮）的長度x成正比，即F=kx，其中k是比例系數(shù)。下面，我們分析并解決這個問題。

用n+1個點(diǎn)x0，x1，x2，…，xi，…，xn，將拉長的長度l分割為等距的n小段，則每小段克服彈力做功近似為

Wi=kxi=k=k.

對n段功求和，得：

Wi=k=ki=k=kl2+kx2.

當(dāng)分割足夠細(xì)的時候，這個和就充分接近我們要求的克服彈力所做的功W，即

W=Wi=（kl2+kl2）=kl2.endprint