高強鋼筋超高性能混凝土梁的使用性能研究

鄧宗才，肖銳，2，徐海賓，陳春生，陳興偉

高強鋼筋超高性能混凝土梁的使用性能研究

鄧宗才1，肖銳1，2，徐海賓1，陳春生3，陳興偉3

（1.北京工業大學城市與工程安全減災省部共建教育部重點實驗室，北京100124；2.中交第一公路工程局國際事業部東非公司，北京100024；3.唐山鋼鐵集團有限責任公司，河北唐山063016）

為研究高強鋼筋超高性能混凝土（ultra-high performance concrete，UHPC）梁的正常使用性能，對6根UHPC梁進行了正截面彎曲性能試驗，總結高強鋼筋UHPC梁的荷載-撓度變化規律，研究其開裂彎矩、短期剛度、裂縫寬度及相應的計算方法。以《混凝土結構設計規范（GB 50010-2010）》為基礎，根據試驗結果回歸出高強鋼筋UHPC梁開裂彎矩的截面抵抗塑性影響系數表達式，確定了高強鋼筋UHPC梁的鋼筋應變不均勻系數、開裂截面內力臂系數和平均綜合應變系數，從而得出高強鋼筋UHPC梁短期剛度的計算公式，并按鋼纖維混凝土計算方法對梁的短期剛度進行了修正計算和對比分析，為實際工程應用提供依據。

超高性能混凝土；高強鋼筋；混凝土梁；開裂彎矩；短期剛度；裂縫寬度；使用性能

20世紀90年代，法國Richard等研制出一種新型建筑復合材料-活性粉末混凝土（reactive powder concrete，RPC）［1］，歐洲將纖維增強RPC稱為超高性能混凝土（ultra-high performance concrete，UHPC），其具有超高抗壓強度和耐久性，鋼纖維的摻入改善了材料韌性，抗疲勞、抗沖擊性能優良。與傳統混凝土相比，UHPC構件的厚度和截面尺寸較小，減輕了構件自重。相同承載力要求下，高強鋼筋替代普通鋼筋可節省鋼筋用量，并降低布筋難度。將高強鋼筋用于抗裂性差的高強混凝土或普通混凝土，由于受到裂縫寬度限制，鋼筋強度難以充分發揮［2］。由于UHPC具有良好的韌性和抗裂性，為高強鋼筋的應用提供了有利條件。通過試驗，明確高強鋼筋UHPC梁的開裂彎矩、短期剛度及裂縫寬度的計算方法。

1 試驗概況

1.1試驗材料與構件制備

用超細水泥替代硅粉制備新型UHPC［3-4］，配合比見表1。其中，超細水泥52.5級，比表面積570 m2／kg；42.5級普通硅酸鹽水泥，比表面積350 m2／kg；S95級粒化高爐礦渣粉，比表面積408m2／kg；40～70目天然石英砂；西卡高效聚羧酸減水劑，按固體摻量計算。UHPC的鋼纖維體積摻率一般為0.5%～3.0%［5］，本試驗按1.5%采用，鋼纖維抗拉強度大于2850MPa，平均長度及長徑比分別為10 mm和60。

表1 構件試驗的SC-RPC配合比Table 1 The mixture proportion of SC-RPC for experimental components

采用攪拌機將拌合物攪拌均勻，攪拌完成后澆筑構件和試塊，并振搗密實。拌合物流動性良好，易施工。待試件具有初始強度后拆模，并采用90℃蒸汽養護3 d。構件的澆筑與養護見圖1。

圖1 構件的澆筑與養護Fig.1 Pouring and curing process of components

試驗得到的UHPC基本力學性能指標為：100 mm邊長立方體抗壓強度平均值140.2 MPa，100 mm×100 mm×300 mm棱柱體軸心抗壓強度均值115.1 MPa，彈性模量Ec為50 GPa；試件抗拉強度試驗方法同文獻［6］，由于使用了較低的鋼纖維體積摻率且纖維長度較短，故抗拉強度實測平均值ft為5.8 MPa。高強鋼筋力學指標測試結果見表2。鋼筋彈性模量Es按《混凝土結構設計規范（GB 50010-2010）》要求取200 GPa［7］。

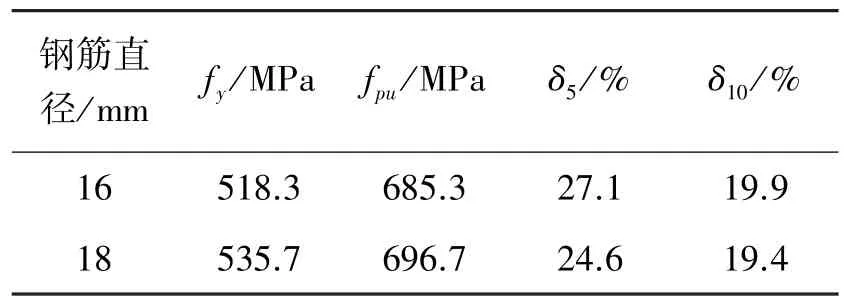
表2 HRB500級高強鋼筋的拉伸性能參數Table 2 Tensile properties of high strength rebars of HRB500

1.2構件設計與試驗方法

試驗梁包括4根矩形梁和2根T形梁，梁長均為3 200 mm，鋼筋采用HRB500級高強鋼筋，沿梁底通長布置。加載裝置與梁截面尺寸見圖2，試驗梁的實際安裝情況見圖3考慮到鋼纖維的增韌作用，配置單排縱筋的梁均未配置箍筋，配置多排縱筋的梁每500 mm設置一直徑6 mm的HPB235箍筋以固定縱筋，保護層厚度10 mm。位移計布置在跨中、加載點和2個支座處，且跨中增設線性差動位移計（LVDT）精確測量試驗梁跨中豎向位移。梁跨中UHPC表面沿截面高度方向及鋼筋表面粘貼應變片。在各級荷載下，采用裂縫寬度觀測儀測量梁體的裂縫寬度。

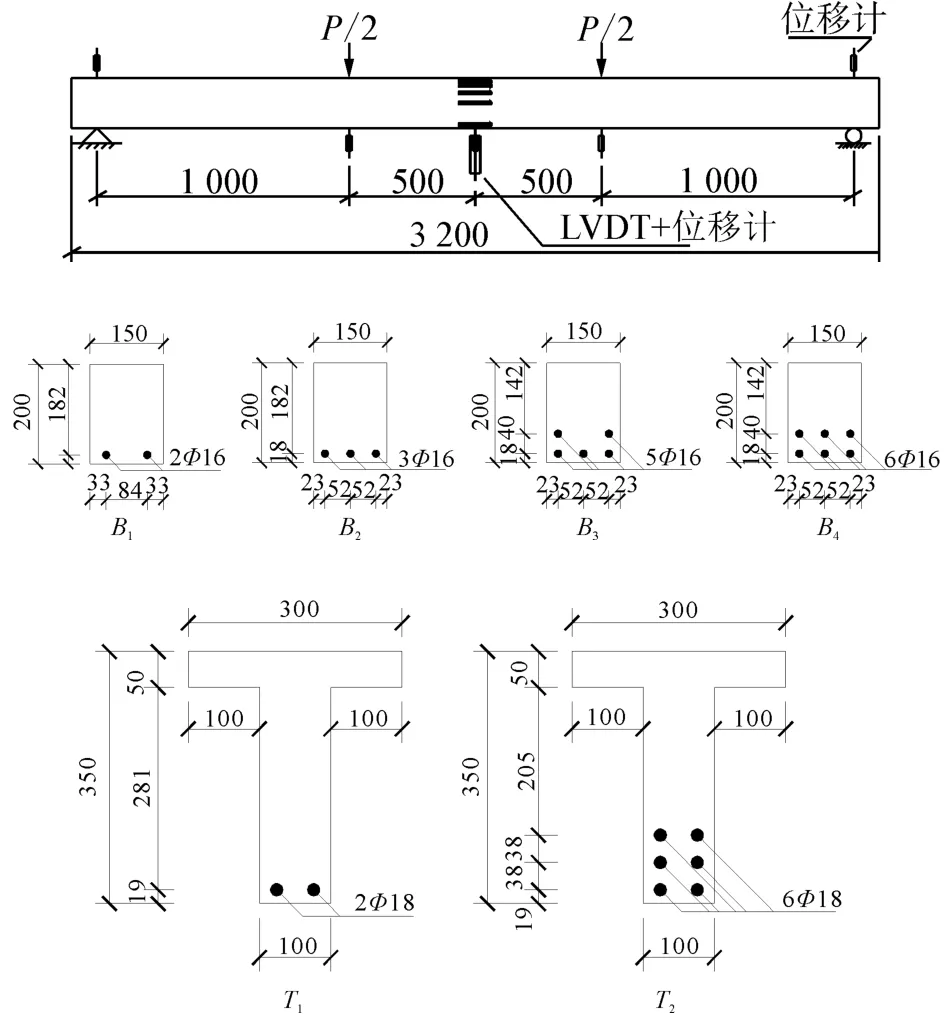
圖2 加載裝置與梁截面尺寸示意圖Fig.2 Test setup and cross section size

圖3 試驗梁安裝實景圖Fig.3 Setup of the test beams

2 試驗結果

梁的荷載-撓度曲線見圖4，梁純彎段裂縫照片見圖5。

由荷載-撓度曲線可知，高強鋼筋UHPC梁的撓度曲線與混凝土梁無本質區別，大致由開裂前、裂縫出現后至鋼筋屈服和鋼筋屈服后3階段組成。

1）加載初期，彎矩小，梁尚未開裂，表現出彈性變形特征，撓度隨荷載線性增長，且梁的剛度不變。

2）達到開裂彎矩后，梁剛度降低，撓度增長速度加快，曲線出現拐點。在純彎段及加載點附近的梁底位置先出現裂縫，裂縫數量、寬度和高度均隨荷載的增長而增加。繼續加載，撓度進一步增加，純彎段裂縫越來越密集，并且剪彎區也逐漸出現裂縫。

3）荷載進一步增大，鋼筋屈服，荷載-撓度曲線上出現拐點，梁的撓度急劇增大而荷載增長很小，曲線水平發展，裂縫在純彎段區域已十分密集；進一步加載，UHPC受壓區局部壓酥，受拉區有主裂縫產生。對于T2梁，由于澆筑缺陷（梁左側加載點位置的上表面略凹）且配筋率較高，荷載達到300 kN時，梁左側加載點靠翼緣兩側產生應力集中，使翼緣與腹板交界處被局部壓裂；當荷載值超過390 kN，位于其下方的UHPC突然撕裂，出現斜拉破壞現象。T2梁剛度計算分析時僅采用局部破壞前的試驗參數作為有效數據。

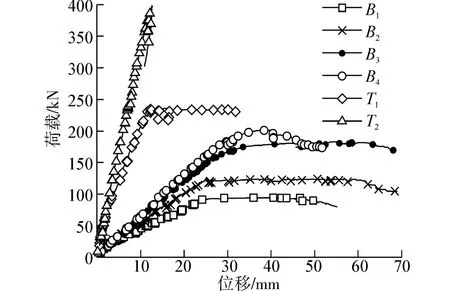
圖4 試驗梁荷載-撓度曲線Fig.4 Load-deflection curves of test beams

圖5 試驗梁裂縫照片Fig.5 Photograph of cracks of test beams

3 開裂彎矩計算分析

水工混凝土及鋼筋混凝土結構設計規范［7-9］中均以材料力學的開裂彈性計算公式為基礎，即假定UHPC開裂時受壓區和受拉區應力圖形均為三角形，并引入截面抵抗塑性影響系數γ（彈塑性抵抗矩與彈性抵抗矩之比）進行修正計算開裂彎矩。

式中：γ可選用混凝土類材料受拉區塑性化的應力圖形進行換算，或使用數理統計方法確定［10］，前者更為嚴謹；后者更為簡便，且可滿足應用要求。故本文選用第2種方法，即根據開裂彎矩和抗拉強度實測結果計算并擬合出其計算公式。

本試驗所用矩形梁截面尺寸和UHPC的抗拉強度測試方法與文獻［6］相同，故采用該文獻值和本文試驗數據推出γ值，并進行分析。文獻［6］采用HRB400級鋼筋，UHPC抗拉強度均值10.2 MPa。回歸分析可知鋼筋級別對UHPC梁的γ值無明顯影響。對于混凝土梁，計算時一般考慮截面高度而不考慮截面形狀對γ的影響，因此本文中截面尺寸對γ的影響也近似認為由截面高度引起。分析發現UHPC梁的截面高度h在小于400 mm時對γ有明顯影響。

由開裂彎矩和抗拉強度實測結果計算的γ及相應的擬合曲線見圖6。

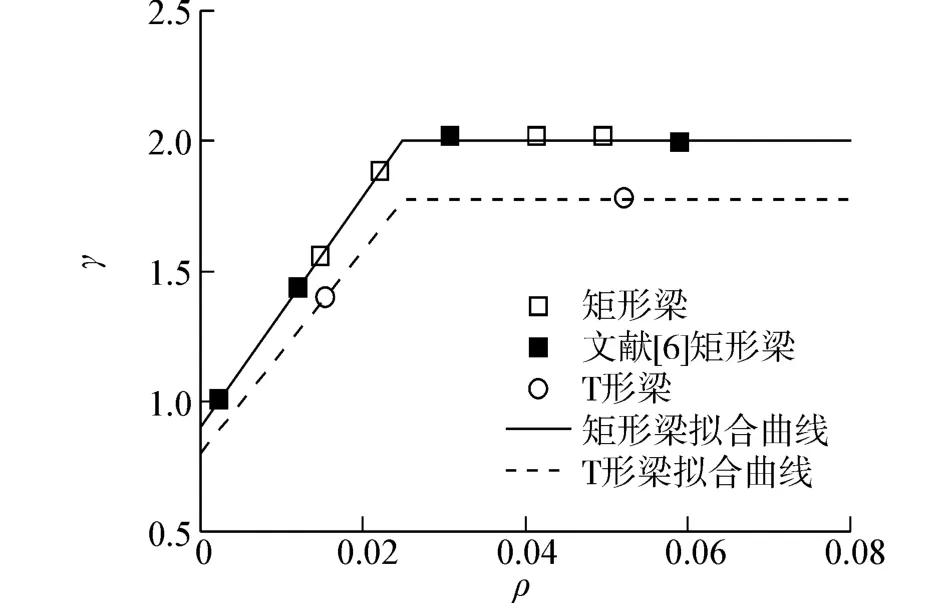
圖6 矩形梁、T形梁配筋率與截面抵抗塑性影響系數關系Fig.6 The relationship between the reinforcement ratio and cross sectional plastic coefficient of rectangular and T shape beams

由于配筋提高了材料的極限變形，強化了UHPC梁受拉區的塑化能力［11］，γ值隨鋼筋用量的增加而增大，并在配筋率達到0.025時趨于穩定。為便于計算和應用，文獻［6，12］的γ曲線均采用二折線。對試驗數據進行擬合分析發現，考慮截面高度和配筋率的影響后，γ曲線計算為

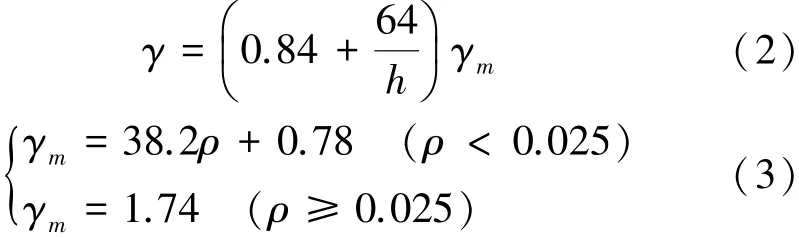
梁的實測開裂彎矩Mct、計算開裂彎矩Mcc及實測值與計算值之比見表3，編號B、T的試驗梁數據來自本次試驗，編號L的矩形試驗梁數據來自文獻［6］。Mct／Mcc的均值為1.0，變異系數0.022，表明計算結果與實測結果符合良好。

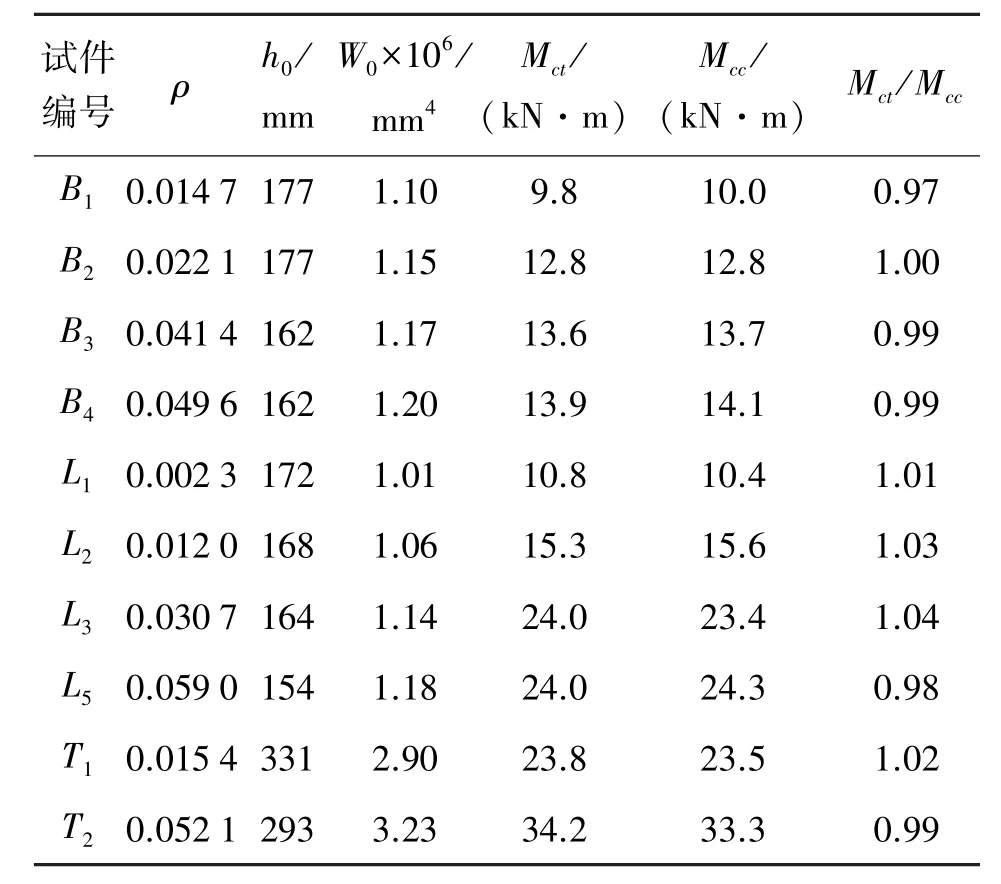
表3 試驗梁開裂彎矩及相關參數Table 3 The crack moment and related coefficients of test beams

4 短期剛度與撓度計算分析

4.1直接計算方法

4.1.1 剛度計算公式的建立

由材料力學和鋼筋混凝土梁的剛度計算基本原理可知，高強鋼筋UHPC受彎梁短期荷載作用下截面抗彎剛度Bsf計算為

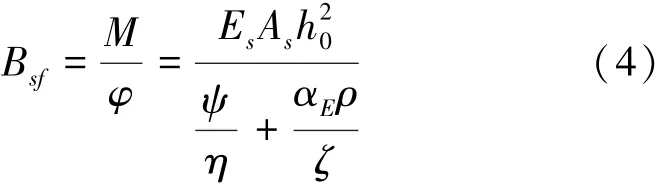
式中：Es為梁受拉鋼筋彈性模量，As為梁受拉鋼筋面積，h0為截面有效高度，ψ為鋼筋應變不均勻系數，η為裂縫截面處的內力臂系數，ζ為UHPC受壓邊緣平均應變綜合系數，αE為梁受拉鋼筋彈性模量與混凝土彈性模量的比值，ρ為梁受拉鋼筋配筋率。

4.1.2 參數ψ、η、ζ的確定

1）受拉鋼筋應變不均勻系數ψ。由于鋼纖維的加入可使構件裂縫變得更加細密均勻，故受拉鋼筋應變不均勻系數ψ仍按《GB 50010-2010》的關系式進行保守計算：

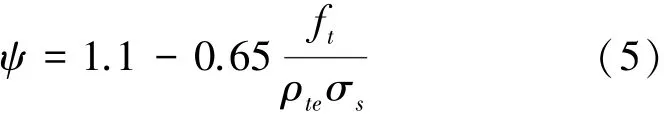
式中：ρte為按有效受拉UHPC截面面積計算的受拉鋼筋配筋率，σs為試驗荷載下構件縱向受拉鋼筋等效應力。

2）開裂截面內力臂系數η。試驗結果表明，與鋼筋混凝土梁相似，在使用荷載下，高強鋼筋UHPC梁處于第2階段工作狀態，截面相對受壓高度ξ變化很小，故內力臂增長不大。本次試驗由實測截面應變得到的η值在0.81～0.91波動，其變化范圍與鋼筋混凝土梁區別很小，故可取與《GB 50010-2010》相同的簡化計算值0.87。

3）受壓UHPC邊緣平均綜合應變系數ζ。ζ= vξωη反映了4個參數對受壓UHPC邊緣平均應變的綜合影響。由平衡關系可知，ζ可由下式求得

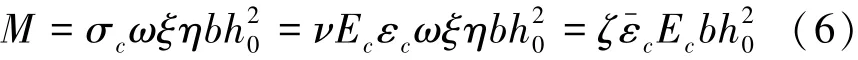
在正常使用階段彎矩（0.5～0.8Mu）范圍，UHPC的受壓應力應變曲線處于線性上升段，該階段彈性系數v（約為1）與應力圖形系數ω（約為0.75）基本恒定，ξ隨M的增長減小，η則隨之變大，且ξ與η在該工作階段的變化不大，兩者作用的結果使M在使用荷載范圍內對ζ的影響不大，故在撓度計算時可假定ζ與M無關，主要取決于UHPC強度、配筋率與受壓區截面形狀。根據式（6）采用使用階段M、實測值計算ζ，并對矩形截面梁進行數據擬合分析得

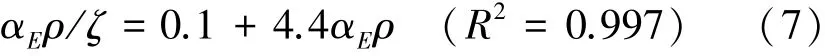
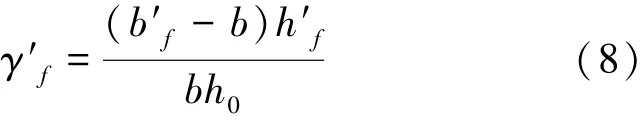
對矩形截面和T形截面梁數據進行擬合分析得

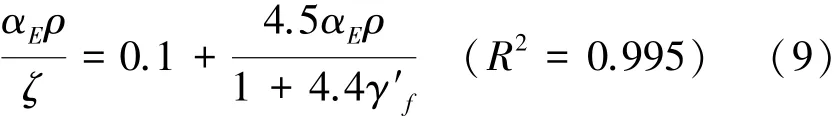
式（9）計算結果與試驗值對比見圖7，可見公式與試驗結果吻合良好。

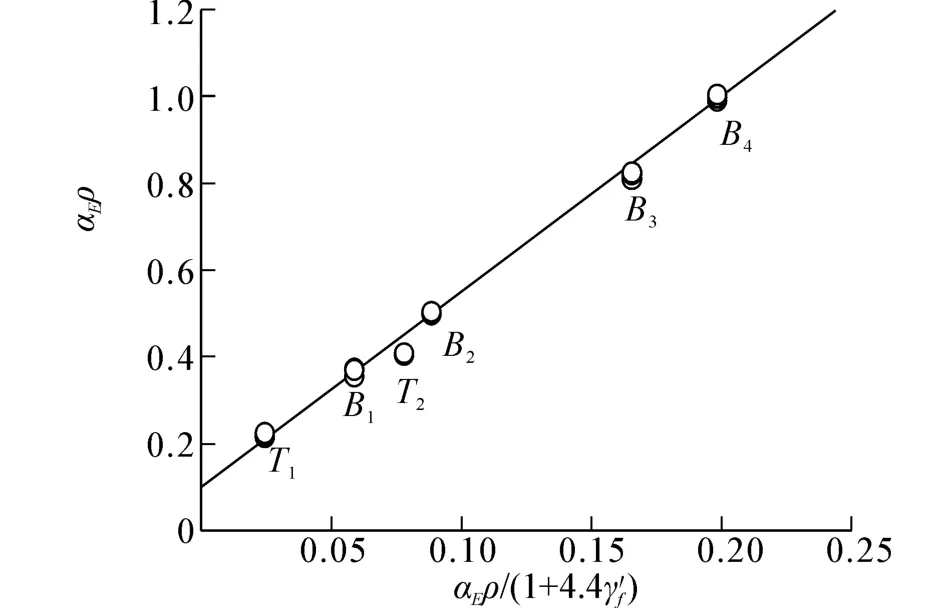
圖7 UHPC受壓邊緣平均綜合應變系數Fig.7 The average integrated strain coefficient at the edge of the UHPC compressive area

4.2簡化計算方法

摻入鋼纖維可使鋼筋混凝土梁的剛度提高10%～40%［13］，可推斷鋼纖維的摻入也是強化UHPC梁剛度的主要因素之一。不考慮鋼纖維對剛度的貢獻，按《GB 50010-2010》計算梁的撓度，發現計算值明顯高于實測值，因此，按照求鋼纖維混凝土梁短期剛度的2個公式［13］分別計算UHPC梁的剛度，以考慮纖維對梁剛度的貢獻：

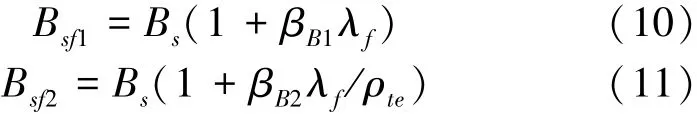
式中：Bsf1、Bsf2分別為考慮鋼纖維對剛度的增強效果簡化修正的UHPC梁短期剛度，Bs按《GB 50010-2010》計算，βB1、βB2為鋼纖維對梁短期剛度的影響系數，主要與鋼纖維品種相關，λf為鋼纖維特征參數，按下式計算：

式中：lf、df、ρf分別為鋼纖維長度、直徑、體積摻率。

本次試驗的λf為0.9。統計分析得到βB1值為0.229，βB2為0.013。

4.3撓度計算結果對比分析

跨中撓度實測值與分別采用Bs、Bsf、Bsf1和Bsf2計算的撓度值對比見表4。可知，采用直接計算方法獲得的短期剛度Bsf和修正剛度Bsf1、Bsf2計算的撓度值與試驗結果吻合均較好。但按《GB 50010-2010》計算的撓度值與實測相比明顯偏大，計算結果過于保守。因此，直接計算方法和兩種修正算法都適于計算高強鋼筋UHPC梁的短期剛度和撓度。相對而言，直接計算方法中各剛度參數均根據試驗和分析得到，修正算法中的式（10）形式上較為簡單，故推薦采用以上2種方法計算短期剛度。

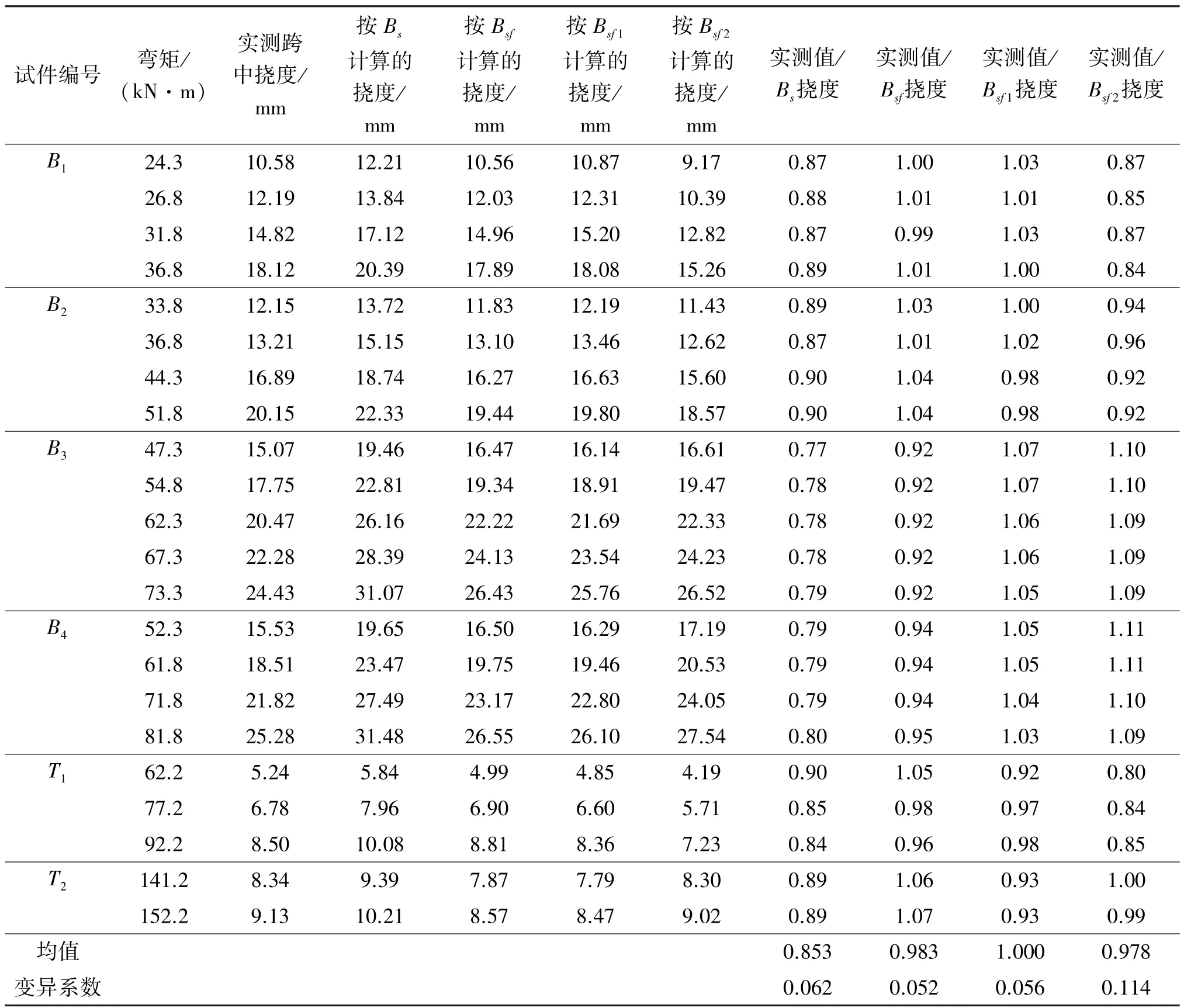
表4 梁跨中撓度實測值與計算結果對比Table 4 Comparison of the test and calculated mid-deflections of beams

5 裂縫寬度計算分析

對于高強鋼筋UHPC梁，決定裂縫寬度的本質特征仍是主裂縫間混凝土與鋼筋的應變差，只是在UHPC基體開裂的基礎上由于鋼纖維的阻裂增韌作用降低了裂縫寬度，故UHPC構件的裂縫寬度以鋼筋混凝土構件的經驗公式為基礎計算：

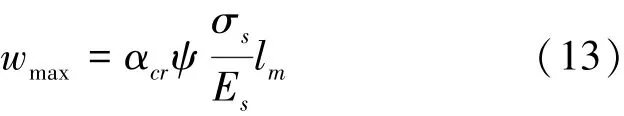
構件受力特征系數αcr的表達式為

本試驗未考慮長期效應，故τ0（長期效應系數）取1，其余參數均按《GB 50010-2010》取值并計算。分析發現，由于鋼纖維的貢獻，將計算的最大裂縫值乘以0.7的修正系數后所得結果與實測梁底跨中純彎段位置最大裂紋寬度符合較好，其實測值與計算值之比的均值為1.0，變異系數0.038。

6 結論

1）高強鋼筋UHPC梁的正截面破壞過程與普通混凝土梁相似，但UHPC梁中鋼纖維的承拉和阻裂作用使梁整體剛度得到了提高。

2）通過擬合分析得到了鋼筋UHPC梁的截面抵抗塑性影響系數，使用該系數計算的開裂彎矩與試驗值吻合良好。

3）分析并確定了高強鋼筋UHPC梁的鋼筋應變不均勻系數、開裂截面內力臂系數和平均綜合應變系數，從而得到了高強鋼筋UHPC梁的短期剛度計算公式。

4）計算發現，計算鋼纖維混凝土結構短期剛度的方法適用于高強鋼筋UHPC梁。

5）高強鋼筋UHPC梁的最大裂縫寬度實測值明顯低于規范《GB 50010-2010》的計算結果，對計算值乘以0.7的修正系數后可用于計算UHPC梁的最大裂縫寬度。

6）由于高強鋼筋UHPC梁的研究樣本較少，ψ的取值偏保守，裂縫寬度計算則需要進一步積累相關試驗數據，以獲得適用性較高的計算參數。

［1］RICHARD P，CHEYREZY M.Composition of reactive powder concretes［J］.Cement and Concrete Research，1995，25（7）：1501-1511.

［2］蔣永生，梁書亭，陳德文，等.高強鋼筋高強混凝土受彎構件的變形性能試驗研究［J］.建筑結構學報，1998，19（2）：37-43.

JIANG Yongsheng，LIANG Shuting，CHEN Dewen，et al.Experimental research for deformation behavior of highstrength concrete flexural member with high-strength rebars［J］.Journal of Building Structures，1998，19（2）：37-43.

［3］肖銳，鄧宗才，申臣良，等.摻超細水泥的新型活性粉末混凝土［J］.混凝土，2013（2）：75-78.

XIAO Rui，DENG Zongcai，SHEN Chenliang，et al.New type of reactive powder concrete with superfine cement［J］.Concrete，2013（2）：75-78.

［4］肖銳，鄧宗才，申臣良.摻超細水泥的經濟型活性粉末混凝土：中國，201210266869.1［P］.2012-11-14.

［5］SCHMIDT M，FEHLING E.Ultra-high-performance concrete：research，development and application in Europe［J］.ACI Special Publication，2005，228：51-78.

［6］李莉.活性粉末混凝土梁受力性能及設計方法研究［D］.哈爾濱：哈爾濱工業大學，2010：29-38.

LI Li.Mechanical behavior and design method for reactive powder concrete beams［D］.Harbin：Harbin Institute of Technology，2010：29-38.

［7］中華人民共和國住房和城鄉建設部.GB 50010-2010，混凝土結構設計規范［S］.北京：中國建筑工業出版社，2010.

［8］水利部長江水利委員會長江勘測規劃設計研究院.SL 191-2008，水工混凝土結構設計規范［S］.北京：中國水利水電出版社，2009.

［9］中交公路規劃設計院.JTG D 62-2004，公路鋼筋混凝土及預應力混凝土橋涵設計規范［S］.北京：人民交通出版社，2004.

［10］陳慰如.以數理統計方法確定矩形截面抵抗矩塑性系數的研究［J］.海洋工程，1989，7（4）：77-86.

CHEN Weiru.Studies on the determining plastic coefficients of section modulus by using statistical analysis method［J］.The Ocean Engineering，1989，7（4）：77-86.

［11］丁自強.水工鋼筋混凝土構件截面抵抗矩塑性系數的計算［J］.鄭州工學院學報，1980（1）：1-23.

DING Ziqiang.Calculating plastic coefficients of section modulus of hydraulic concrete components［J］.Journal of Zhengzhou Institute of Technology，1980（1）：1-23.

［12］陸小呂.活性粉末混凝土矩形截面配筋梁正截面受彎的計算方法研究［D］.北京：北京交通大學，2011：44-51.

LU Xiaolv.Study of the calculating method of crack resistance and flexural capacity for rectangular reinforced RPC beam［D］.Beijing：Beijing Jiaotong University，2011：44-51.

［13］黃承逵.纖維混凝土結構［M］.北京：機械工業出版社，2004：24-33.

Serviceability research of ultra-high performance concrete beams reinforced with high strength steel bars

DENG Zongcai1，XIAO Rui1，2，XU Haibin1，CHEN Chunsheng3，CHEN Xingwei3
（1.Key Laboratory of Urban Security and Disaster Engineering，Ministry of Education，Beijing University of Technology，Beijing 100124，China；2.Overseas Company，China First Highway Engineering Co.，Ltd.，Beijing 100024，China；3.Tangshan Iron and Steel Group Co.Ltd.，Tangshan 063016，China）

To study the serviceability of ultra-high performance concrete（UHPC）beams reinforced with high strength steel bars，the flexural properties of six UHPC beams were tested.Then the change law of load-deflection of the UHPC beam was concluded，the cracking moment，the short term stiffness and cracking width，and the calculation methods were summarized.Based on the code for design of concrete structures（GB 50010-2010），the cross sectional plastic coefficient influencing the regression equation of UHPC beam′s cracking moment was concluded，the rebar nonuniform coefficient of UHPC beam，the internal lever arm coefficient of cracking cross section，and the average integrated strain coefficient were ascertained to calculate the beam′s short term stiffness.The beam′s short term stiffness was calculated and compared，based on the adjusted calculating method for steel fiber reinforced concrete.In addition，a modified cracking width calculation formula was generated.

ultra-high performance concrete；high strength steel bar；concrete beam；crack moment；short time stiffness；cracking width；serviceability

10.11990／jheu.201404077

http：／／www.cnki.net／kcms／detail／23.1390.U.20150907.1713.018.html

TU 528.31

A

1006-7043（2015）10-1335-06

2014-04-25.網絡出版時間：2015-09-01.

國家自然科學基金資助項目（51378032）；教育部博士點基金資助項目（20131103110017）；北京市自然科學基金資助項目（8142005）.

鄧宗才（1961-），男，教授，博士生導師；

肖銳（1984-），男，博士.

肖銳，E-mail：xrxiaorui＠163.com.