基于構(gòu)筑模型的植物動(dòng)態(tài)生長(zhǎng)研究*
王甜甜,馬學(xué)強(qiáng),代曉琳
(1.山東師范大學(xué)信息科學(xué)與工程學(xué)院,山東濟(jì)南250014;2.山東省分布式計(jì)算機(jī)軟件新技術(shù)重點(diǎn)實(shí)驗(yàn)室,山東濟(jì)南250014)
基于構(gòu)筑模型的植物動(dòng)態(tài)生長(zhǎng)研究*
王甜甜1,2,馬學(xué)強(qiáng)1,2,代曉琳1,2
(1.山東師范大學(xué)信息科學(xué)與工程學(xué)院,山東濟(jì)南250014;2.山東省分布式計(jì)算機(jī)軟件新技術(shù)重點(diǎn)實(shí)驗(yàn)室,山東濟(jì)南250014)
植物學(xué)家提出的23種結(jié)構(gòu)定義了植物形態(tài)發(fā)生的方式和最終生長(zhǎng)的形態(tài),能夠形象而準(zhǔn)確地對(duì)植物形態(tài)發(fā)生進(jìn)行歸納和分類(lèi),但缺乏對(duì)植物形態(tài)可視化表達(dá)的有效手段和方法。因此,本文為再現(xiàn)植物的動(dòng)態(tài)生長(zhǎng)過(guò)程,基于構(gòu)筑模型,遵循雙尺度自動(dòng)機(jī)的基本原理,應(yīng)用微分L-系統(tǒng)構(gòu)建植物連續(xù)生長(zhǎng)過(guò)程的動(dòng)態(tài)模型,并在計(jì)算機(jī)進(jìn)行了三維可視化實(shí)現(xiàn)。提出的方法拓展了構(gòu)筑模型的應(yīng)用,仿真結(jié)果表明該方法在植物形態(tài)的建模上確實(shí)行之有效。
構(gòu)筑模型;雙尺度自動(dòng)機(jī);微分L-系統(tǒng);動(dòng)態(tài);三維
0 引言
植物動(dòng)態(tài)生長(zhǎng)模型是指利用計(jì)算機(jī)形象直觀地再現(xiàn)植物生長(zhǎng)過(guò)程。在計(jì)算機(jī)建模時(shí),如何形象地體現(xiàn)植物的這種“生命”特征,使植物真正具有生長(zhǎng)的現(xiàn)象已成為研究者廣泛關(guān)注的焦點(diǎn)。因此,植物的模擬是在植物生長(zhǎng)特征表達(dá)的基礎(chǔ)上實(shí)現(xiàn)從拓?fù)浣Y(jié)構(gòu)到幾何形態(tài)建模的過(guò)程[1]。植物學(xué)家以分類(lèi)為目的,提出的植物構(gòu)筑模型是指植物形態(tài)發(fā)生的方式以及最終長(zhǎng)成的形態(tài)[2]。根據(jù)植物構(gòu)造模型可以在一個(gè)更高的層次上準(zhǔn)確地描述植物的結(jié)構(gòu)特點(diǎn),分析和模擬植物的生長(zhǎng)過(guò)程,該項(xiàng)研究被認(rèn)為是植物拓?fù)浣Y(jié)構(gòu)研究中的經(jīng)典工作[3]。
為了實(shí)現(xiàn)從拓?fù)浣Y(jié)構(gòu)到幾何形態(tài)建模的過(guò)程,國(guó)內(nèi)外研究學(xué)者提出了多種植物建模方法,其中以著名的L-系統(tǒng)的出現(xiàn)為標(biāo)志。最初的L-系統(tǒng)是D0L系統(tǒng),它只能描述形狀規(guī)則的植物模型[4]。之后,加拿大學(xué)者Prusinkiewicz對(duì)L-系統(tǒng)進(jìn)行了擴(kuò)展,提出開(kāi)放L-系統(tǒng)(Open L-system)[5]和隨機(jī)L-系統(tǒng)(Stochastic L-system)[6]以及微分L-系統(tǒng)等[7]。在此期間又出現(xiàn)了基于分形理論的一系列植物建模方法,如疊代函數(shù)系統(tǒng)(IFS)、分支矩陣、粒子系統(tǒng),以及由DeReffye提出的自動(dòng)機(jī)模型(參考軸技術(shù))和在此基礎(chǔ)上進(jìn)一步發(fā)展提出的雙尺度自動(dòng)機(jī)模型等。其中微分L-系統(tǒng)是一種發(fā)展得較完善的L-系統(tǒng)方法,是參數(shù)L-系統(tǒng)的擴(kuò)展[8]。在該系統(tǒng)中,產(chǎn)生式用于表達(dá)模型數(shù)量上的變化(比如植物新分支的產(chǎn)生),而微分方程求解過(guò)程則描述連續(xù)生長(zhǎng)過(guò)程(比如莖的漸漸伸長(zhǎng))。雙尺度自動(dòng)機(jī)模型是為了表現(xiàn)植物的生長(zhǎng)機(jī)理,由趙星等人從植物學(xué)的角度提出的。盡管各種建模方法的目的和尺度不同,在建模原理和仿真的真實(shí)性要求上有很大的差異,但在計(jì)算機(jī)建模時(shí),如何形象地體現(xiàn)植物的“生命”特征,使植物真正具有生長(zhǎng)的現(xiàn)象已成為研究者共同關(guān)注的焦點(diǎn)。
綜上可知,構(gòu)筑模型能夠給出植物形態(tài)發(fā)生方式和最終形態(tài),但并不能體現(xiàn)出植物生長(zhǎng)過(guò)程的周期性,且缺乏對(duì)植物形態(tài)可視化表達(dá)的有效手段和方法,微分L-系統(tǒng)雖然可以進(jìn)行可視化表達(dá),但其必須基于確定生長(zhǎng)算法。因此本文在構(gòu)筑模型的基礎(chǔ)上進(jìn)一步引入雙尺度自動(dòng)機(jī)原理,給出更能表達(dá)植物真實(shí)生長(zhǎng)過(guò)程的動(dòng)態(tài)生長(zhǎng)算法,并使用微分L-系統(tǒng)進(jìn)行描述,最終形成一個(gè)基于構(gòu)筑模型的完整連續(xù)且具有周期性的動(dòng)態(tài)發(fā)生模型。
1 植物形態(tài)發(fā)生的基本原理
1.1 節(jié)周期、生理周期
植物的主體結(jié)構(gòu)由軸組成,植物的主干稱(chēng)為主軸;分枝用不同級(jí)的軸命名,如1級(jí)側(cè)軸、2級(jí)側(cè)軸等。如圖1所示,軸上生葉的部位稱(chēng)為節(jié),節(jié)與節(jié)之間的那段軸稱(chēng)為節(jié)間。一般來(lái)說(shuō)節(jié)和節(jié)間以及節(jié)上的側(cè)生器官(葉、花或者果實(shí))的集合,植物學(xué)上稱(chēng)為植物分生單位,長(zhǎng)成一個(gè)新分生單位的時(shí)間稱(chēng)之為節(jié)周期(Syllepticshoot)[10]。

圖1 軸結(jié)構(gòu)特征(引自文獻(xiàn)[9])
另外,將枝條開(kāi)始生長(zhǎng)到產(chǎn)生分支之前的這段時(shí)間稱(chēng)為一個(gè)生理周期。每個(gè)生理周期包含若干個(gè)節(jié)周期,節(jié)周期長(zhǎng)短及每個(gè)生理周期包含節(jié)周期數(shù)視不同植物而定。在此,選擇的Leeuwenberg模型的生長(zhǎng)特征為:每個(gè)生長(zhǎng)單元都生有花序,而生長(zhǎng)單元的生長(zhǎng)就終止于花序,因此,參考現(xiàn)在比較流行的觀點(diǎn):將花朵看成一個(gè)節(jié)點(diǎn)縮短的變態(tài)短枝。在對(duì)模型進(jìn)行周期性劃分時(shí),特別將生殖生長(zhǎng)階段作為一個(gè)單獨(dú)的節(jié)周期來(lái)處理[11]。
1.2 生長(zhǎng)函數(shù)
植物生長(zhǎng)動(dòng)態(tài)模擬過(guò)程中,對(duì)于植物量形成規(guī)律的描述,常需要借助于數(shù)學(xué)模型[12]。實(shí)驗(yàn)中把節(jié)間生長(zhǎng)的時(shí)間與生長(zhǎng)長(zhǎng)度的關(guān)系用直角坐標(biāo)圖來(lái)表示,就會(huì)得到一條形狀像“S”的曲線,這條S曲線即為節(jié)間生長(zhǎng)曲線。進(jìn)一步的研究發(fā)現(xiàn)許多植物在其節(jié)周期內(nèi)的生長(zhǎng)過(guò)程遵循這個(gè)模式,為了得到一個(gè)最為合適的函數(shù)模型,進(jìn)行了大量的研究。最終,決定利用“S”型玻爾茲曼函數(shù)[13],這個(gè)函數(shù)形式如下:

其中A是節(jié)間最大或最終長(zhǎng)成后的尺寸,tm是當(dāng)其長(zhǎng)到最大尺寸的一半時(shí)所用的時(shí)間,k控制其相關(guān)的生長(zhǎng)率,也可以看作是特定的生長(zhǎng)率。每一個(gè)生長(zhǎng)模塊(如莖稈、花朵、葉片)具有不同的生長(zhǎng)速率,因此需要使用不同的數(shù)學(xué)模型來(lái)描述(在此主要由不同的k值體現(xiàn))。例如大多數(shù)大戟科植物主干生長(zhǎng)速率k為0.6±0.07d-1[10],則其生長(zhǎng)函數(shù)為:

對(duì)應(yīng)的線性圖像如圖2。
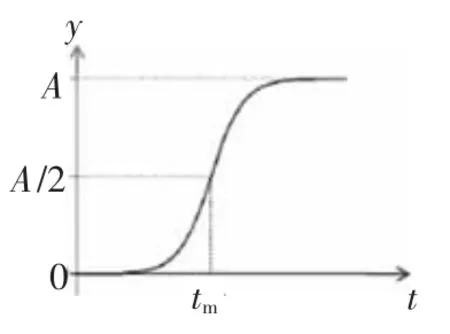
圖2 生長(zhǎng)函數(shù)圖像


由方程(1)所示的節(jié)間生長(zhǎng)函數(shù)可知其微分形式為:其中y是關(guān)于t的函數(shù),代表生長(zhǎng)函數(shù),結(jié)合有限差分方法,且在方程(4)中使用從t軸上等距抽樣得來(lái)的數(shù)值:tj=t0+jΔt(j=0,1,…),并在區(qū)間[tn,tn+1]中近似地使用差商代替微商,因此方程(4)最終可以寫(xiě)為:
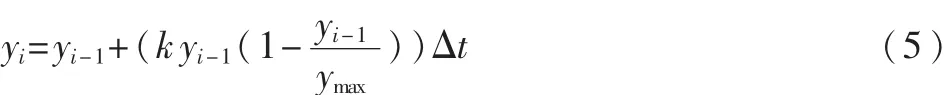
進(jìn)一步推導(dǎo)可得:
對(duì)于任意的i值,可以將方程(5)看做分配一個(gè)新值yi到變量yi-1,并在前鄰采樣點(diǎn)取值yi-1。t軸上的任意采樣點(diǎn)(除了邊界值)屬性作用類(lèi)似,因此方程(4)可以寫(xiě)成L-系統(tǒng)產(chǎn)生式的形式:
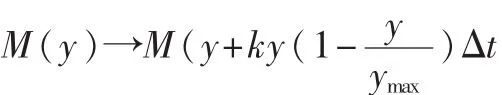
上面僅僅是一部分,而一個(gè)用于求解方程(2)的完整L-系統(tǒng)必須滿(mǎn)足:
(1)為m個(gè)模塊中的來(lái)自公理的M模塊創(chuàng)建一個(gè)初始字符串;
(2)為變量y在每個(gè)模塊都設(shè)定一個(gè)初值;
(3)在模塊M的單步推導(dǎo)過(guò)程中維持變量y的初值和終值。
2 構(gòu)筑模型
大千世界的植物種類(lèi)繁多,為了便于歸納和分類(lèi),植物學(xué)家給出下述四組簡(jiǎn)單形態(tài)描述:(1)分支方式;(2)軸的形態(tài)特征;(3)性特征位置;(4)生長(zhǎng)模式[14]。將其中的一組或者幾組進(jìn)行組合,可以得到龐大的組合數(shù)目。然而在自然界僅發(fā)現(xiàn)23種植物構(gòu)造模型,為了不額外增大植物學(xué)名詞量從而增加記憶負(fù)擔(dān),每種構(gòu)筑模型都以植物學(xué)家的名字命名[2,9]。如Holttum模型、Corner模型、Tomlinson模型等。自然界中任何一種植物都可以由其中一種或者幾種模型組合進(jìn)行描述。
本文主要研究大戟科植物,因此需要用Leeuwenberg模型描述,該模型主要特點(diǎn)為合軸非線性分支,每個(gè)模塊有兩個(gè)或多個(gè)分支,后繼模塊重復(fù)其父模塊的生長(zhǎng)發(fā)育特點(diǎn),但是這個(gè)重復(fù)是定性的,非定量的,表現(xiàn)為:后繼模塊的長(zhǎng)度和分叉角度是遞減的。圖3為植物學(xué)家給出的Leeuwenberg模型的圖形化描述。
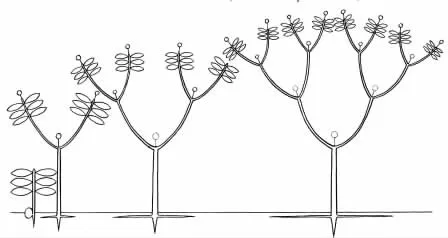
圖3 Leeuwenberg模型
通過(guò)這些模型,植物學(xué)家不僅形象而又準(zhǔn)確地描述了各種類(lèi)型植物的形態(tài)結(jié)構(gòu)特點(diǎn),而且進(jìn)一步研究了植物的生長(zhǎng)過(guò)程及其生長(zhǎng)規(guī)律,這些結(jié)構(gòu)模型對(duì)樹(shù)木狀和草本狀植物都適用。因此,利用植物的構(gòu)造模型,對(duì)植物形態(tài)進(jìn)行仿真,不失為一種簡(jiǎn)便快捷而又有效的方法[14]。
然而構(gòu)筑模型不能體現(xiàn)植物生長(zhǎng)過(guò)程中表現(xiàn)出來(lái)的明顯周期性特性,因此要結(jié)合雙尺度自動(dòng)機(jī)原理得出更貼近植物真實(shí)生長(zhǎng)過(guò)程的動(dòng)態(tài)生長(zhǎng)算法,這樣可以有效增強(qiáng)整個(gè)動(dòng)態(tài)模型的真實(shí)感。
3 微分L-系統(tǒng)
在對(duì)植物動(dòng)態(tài)生長(zhǎng)研究過(guò)程中,尋找一種方法來(lái)對(duì)植物形態(tài)進(jìn)行可視化表達(dá),從而建立更逼真、完整、有效的植物生長(zhǎng)模型是必要的。在此選用微分L-系統(tǒng)進(jìn)行表達(dá),它將傳統(tǒng)的L-系統(tǒng)產(chǎn)生式和微分方程合為一體,成功模擬了植物生長(zhǎng)過(guò)程中的離散、連續(xù)情況。
微分L-系統(tǒng)是在參數(shù)化L-系統(tǒng)的基礎(chǔ)上,通過(guò)引入連續(xù)的時(shí)間流的信息來(lái)取代一系列離散變換過(guò)程,比如,模塊A(w)只要參數(shù)w的取值范圍在定義域DA中,這個(gè)模塊就會(huì)連續(xù)地變化,如果w的值達(dá)到了DA邊界,就會(huì)觸發(fā)一個(gè)產(chǎn)生式產(chǎn)生離散的變換,這個(gè)時(shí)候A(w)就會(huì)被其子孫模塊替換[8]。
在tα?xí)r刻模塊A的結(jié)構(gòu)可以用一個(gè)連續(xù)的字符串表示:u=A1(w1)A2(w2)…An(wn)。其模塊增量的產(chǎn)生可能與其緊鄰的前后兩個(gè)模塊有關(guān)系,也可能只與其中的某個(gè)模塊有關(guān),也可能只與該模塊本身狀態(tài)有關(guān)。在此假設(shè)后一個(gè)模塊增量的產(chǎn)生只與其緊鄰的前一個(gè)模塊狀態(tài)有關(guān),在此稱(chēng)之為其左鄰居(沒(méi)有左鄰居的第一個(gè)模塊其w值為預(yù)先給出的定值),在上式中,Ai-1(wi-1)是Ai(wi)的左鄰居,下面用l來(lái)指代A(w)的左鄰居。
A(w)模塊內(nèi)部的連續(xù)變化規(guī)律可以通過(guò)w關(guān)于時(shí)間t的微分方程來(lái)描述,其微分方程為:
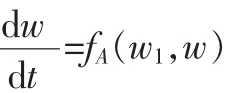
只要A(w)模塊中的參數(shù)w的取值范圍在A(w)的定義域DA中,模塊就會(huì)根據(jù)上面的微分方程變化,DA是一個(gè)開(kāi)區(qū)間,CA是DA的邊界,有m段互不相交的段組成,記為CA。如果式子lim A(w)∈CA成立,則用A(w)的
k
子孫替換掉A(w),A(w)在時(shí)刻tβ時(shí)的產(chǎn)生式:PA=A
k
(ω):條件表達(dá)式→Bk,1(wk,1)Bk,2(wk,2)…Bk,m(wk,m),
kk
其中A(w)稱(chēng)為前驅(qū),后面跟有條件表達(dá)式,最后的Bk,1(wk,1)Bk,2(wk,2)…Bk,m(wk,m)稱(chēng)為后繼,k可以取大于
kk
1的任意正數(shù)值表明以A(w)為前驅(qū)的產(chǎn)生式可能不止一個(gè),當(dāng)w到達(dá)不同區(qū)域的邊界CA時(shí),就使用不同的產(chǎn)
k生式。
總之,微分L-系統(tǒng)通過(guò)把微分方程引入到參數(shù)L-系統(tǒng)中,用來(lái)描述植物生長(zhǎng)過(guò)程中的器官的連續(xù)變化性質(zhì),是對(duì)參數(shù)L-系統(tǒng)進(jìn)行植物建模的擴(kuò)展。
4 植物的動(dòng)態(tài)生長(zhǎng)模型
為了快速有效地模擬大戟科植物動(dòng)態(tài)生長(zhǎng)過(guò)程中的生長(zhǎng)細(xì)節(jié)和生長(zhǎng)特性,在Leeuwenberg模型的基礎(chǔ)上,遵循雙尺度自動(dòng)機(jī)原理對(duì)植物動(dòng)態(tài)生長(zhǎng)模型進(jìn)行構(gòu)建,其算法過(guò)程如圖4所示。
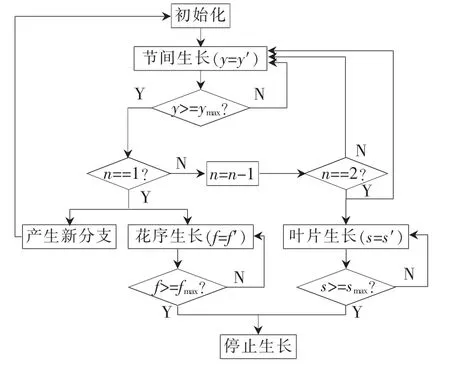
圖4 生長(zhǎng)算法過(guò)程設(shè)計(jì)
基于以上生長(zhǎng)算法,選用微分L-系統(tǒng)具體到每個(gè)節(jié)間的生長(zhǎng)細(xì)節(jié)來(lái)模擬整個(gè)生長(zhǎng)過(guò)程。為了實(shí)現(xiàn)這個(gè)目標(biāo),設(shè)定每個(gè)節(jié)間長(zhǎng)度、葉片大小及花序大小的初值均大于0,其邊界值為定值,在一個(gè)生理周期(包含n個(gè)節(jié)周期)內(nèi)節(jié)間長(zhǎng)度一定。
基于以上分析和假設(shè)最終形成的微分L-系統(tǒng)形式如下:
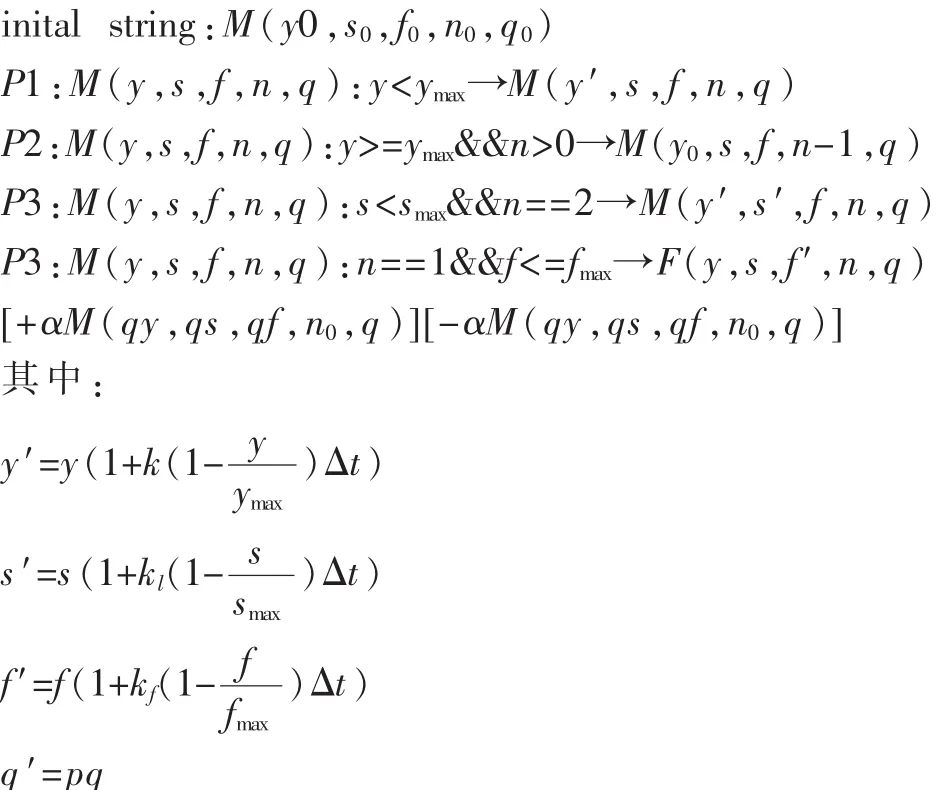
將每個(gè)生理周期生長(zhǎng)單元看作一個(gè)模塊M,參數(shù)y代表節(jié)間的長(zhǎng)度,s是葉片大小,f是花序當(dāng)前生長(zhǎng)量,n為一個(gè)生理周期包含的若干個(gè)節(jié)周期。而其營(yíng)養(yǎng)生長(zhǎng)和生殖生長(zhǎng)速率的不同用不同的k值界定(節(jié)間為k,葉片為kl,花序?yàn)閗f)。p1主要是指節(jié)間從初始長(zhǎng)度y0到最大長(zhǎng)度ymax的連續(xù)生長(zhǎng)過(guò)程;p2指本節(jié)間生長(zhǎng)完成進(jìn)入下一個(gè)節(jié)周期;p3指在該生理周期的倒數(shù)第二個(gè)節(jié)周期內(nèi)同時(shí)進(jìn)行莖稈和葉片的生長(zhǎng);p4指本生長(zhǎng)單元營(yíng)養(yǎng)生長(zhǎng)完成進(jìn)入生殖生長(zhǎng)階段;p5代表產(chǎn)生新的分支;y′,f′,s′方程主要管理節(jié)間、花序和葉片具體生長(zhǎng)節(jié)奏,一般約定y、f、s初值恒為正數(shù),p用于控制參數(shù)q的變化情況。
5 模型仿真
應(yīng)用該方法在VS2010+openGL環(huán)境下實(shí)現(xiàn)的Leeuwenberg模型在5個(gè)生理周期內(nèi)的生長(zhǎng)細(xì)節(jié)如圖5、圖6、圖7所示。
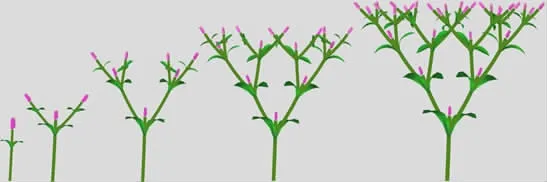
圖5 正視圖

圖6 側(cè)視圖

圖7 俯視圖
6 結(jié)論
綜上所述,模擬植物的真實(shí)動(dòng)態(tài)生長(zhǎng)過(guò)程,應(yīng)該采用基于植物生長(zhǎng)原理的模型(在此采用Leeuwenberg模型),因其能夠準(zhǔn)確描述植物生長(zhǎng)過(guò)程及其生長(zhǎng)規(guī)律,而與雙尺度自動(dòng)機(jī)原理的結(jié)合更有助于表達(dá)植物生長(zhǎng)細(xì)節(jié)和生長(zhǎng)特性。另外,這種將參數(shù)L-系統(tǒng)與微分方程結(jié)合并綜合考慮了植物生長(zhǎng)特征形成的新式微分L-系統(tǒng),在表述植物生長(zhǎng)過(guò)程時(shí)的主要優(yōu)點(diǎn)是:其可以將植物的生長(zhǎng)過(guò)程細(xì)化到每個(gè)節(jié)周期,而其中的參數(shù)可控性更是使處于不同生理周期的節(jié)間的不同生長(zhǎng)特性得以體現(xiàn)。其能夠更加真實(shí)具體地反應(yīng)植物的動(dòng)態(tài)生長(zhǎng)過(guò)程,尤其是“S”型玻爾茲曼函數(shù)的使用,使得對(duì)于節(jié)間生長(zhǎng)過(guò)程的模擬更加貼近真實(shí)。
[1]HONDA H,HATTA H.Branch geometry in cornus kousa(Cornaceae):computer simulation[J].American Journal of Botany,1997,84(6):745-755.
[2]HALLE F,OLDEMAN R A A,TOMLINSON P B.Tropical trees and forests:an architectural analysis[M].Berlin:Springer Verlag,1978.
[3]趙星.忠實(shí)于植物學(xué)的虛擬植物生長(zhǎng)研究[D].合肥:中國(guó)科技大學(xué),2001.
[4]NDENMAY A.Mathematical models for cellular interaction in development,parts I and II[J].Journal of Theoretical Biology,1968(18):280-315.
[5]MéCH R,PRUSINKIEWICZ P.Visual models of plants interacting with their environment[C].Proceedings of the 23rd Annual Conferenceon Computer Graphics and Interactive Techniques,1996:397-410.
[6]PRUSINKIEWIEZ P,LINDENMAYER A.The algorithmic beauty of plants[M].Spring-Verleg,1990.
[7]PRUSINKIEWICZ P,F(xiàn)EDERL P,KARWOWSKI R,et al. L-systems and beyond[J].Course notes from SIGGRAPH,2003(5):70-82.
[8]PRUSINKIEWICZ P,HAMMEL M,MJOLSNESS E.Animation of plant development[J].Computer Graphics,1993,27(3):351-360.
[9]DE REFFYE P,EDELIN C,F(xiàn)RAN?ON J,et al.Plant models faithful to botanical structure and development[C]. ACM SIGGRAPH Computer Graphics,1988,22(4):151-158.
[10]趙星,DE REFFYE P,熊范倫,等.虛擬植物生長(zhǎng)的雙尺度自動(dòng)機(jī)模型[J].計(jì)算機(jī)學(xué)報(bào),2001,24(6):609-615.
[11]敬松,方逵,陳演,等.圖像與L-系統(tǒng)相結(jié)合的柑橘葉片形態(tài)特征重構(gòu)研究[J].農(nóng)機(jī)化研究,2012,34(5):65-67,71.
[12]包鋼,趙星,閆紅平.植物生長(zhǎng)建模與可視化—回顧與展望[J].自動(dòng)化學(xué),2001,27(6):816-835.
[13]MüNDERMANN L,ERASMUS Y,LANE B,et al. Quantitative modeling of arabidopsis development[J].Plant Physiology,2005,139(2):960-968.
[14]丁維龍.虛擬植物生長(zhǎng)模型及其與智能系統(tǒng)集成研究[D].合肥:中國(guó)科學(xué)技術(shù)大學(xué),1999.作者簡(jiǎn)介:
Research on plant development based on structural model
Wang Tiantian1,2,Ma Xueqiang1,2,Dai Xiaolin1,2
(1.School of Information Science and Engineering,Shandong Normal University,Ji′nan 250014,China;2.Distributed Computer Software in Shandong Province Key Laboratory of New Technology,Ji′nan 250014,China)
The twenty-three kinds of structures defined by the botanists proposed the way of plant morphogenesis and the final form of the growth.They are able to induce and group by plant morphogenesis vividly and accurately,but they are lack of effective means and methods on the expression of plant morphology visualization.Therefore,in this paper,application of differential L-system builds the dynamic model of plant continuous growth process based on the basic principles to construct the model,dual scale automaton model for the purpose of reappearing reproduction of plant dynamic growth process,and 3D visualization is realized in computer.The proposed method extends the application to build a model,the simulation results confirm that the method is indeed effective in modeling of plant form.
structural model;dual-scale automation;differential L-system;dynamic;three-dimensional
TP391
A
1674-7720(2015)13-0024-04
雙尺度自動(dòng)機(jī)原理,勢(shì)必要用到描述植物周期的一系列概念。下面將對(duì)之后要用到的周期性概念做出詳細(xì)的定義描述。
2015-03-06)
山東省高等學(xué)校科技計(jì)劃項(xiàng)目(J14LN09)
王甜甜(1989-),女,碩士研究生,主要研究方向:虛擬植物建模。
馬學(xué)強(qiáng)(1970-),通訊作者,男,副教授,碩士生導(dǎo)師,主要研究方向:虛擬植物模型、進(jìn)化計(jì)算。E-mail:sdnumxq@qq.com。
代曉琳(1991-),女,碩士研究生,主要研究方向:虛擬植物建模。

