分裂導線平均風荷載阻力系數干擾效應研究

左太輝, 牛華偉, 閔 絢3, 華旭剛

(1.廣東省建筑科學研究院集團股份有限公司, 廣州 510050; 2. 湖南大學風工程試驗研究中心, 長沙 410082; 3. 中國電力科學研究院, 武漢 430074)

分裂導線平均風荷載阻力系數干擾效應研究

左太輝1,*, 牛華偉2, 閔 絢3, 華旭剛2

(1.廣東省建筑科學研究院集團股份有限公司, 廣州 510050; 2. 湖南大學風工程試驗研究中心, 長沙 410082; 3. 中國電力科學研究院, 武漢 430074)

分裂導線在不同風場條件下的阻力系數及干擾效應對導線風荷載的合理化設計十分重要。不同迎風角和雷諾數下分裂導線氣動阻力系數特性及干擾屏蔽效應比較復雜。為了研究該干擾效應，設計長細比約為1∶30、長度約為1m的導線節段模型試驗，獲得導線平均風荷載阻力系數隨雷諾數、尾流干擾的變化規律；進行了不同風速和迎風方向下4、6和8分裂導線節段模型平均風荷載阻力系數試驗，總結了多分裂導線阻力系數的屏蔽效應規律特性。試驗結果表明，多分裂導線氣動阻力系數干擾效應明顯，且不同迎風方式對風荷載影響較大，風荷載明顯低于現行規范規定值。分裂導線風荷載合理化設計和計算應該重視迎風角度和干擾效應的影響。

風荷載；氣動阻力系數；分裂導線；風洞試驗；干擾屏蔽效應

0 引 言

由于導線間隔棒間距、子導線的間距和迎風角度等分裂導線自身參數的復雜性，類圓柱形的導線風荷載氣動阻力系數隨雷諾數、迎風角度、風速的變化比較明顯，影響導線風荷載設計，也誘導了一些和導線氣動特性有關的振動。

導線的平均風荷載阻力系數不僅是建立輸電線路風荷載模型的主要參數，更是特高壓輸電線路風致振動的關鍵影響因素。近年來一些風、雪等自然災害致倒塔和斷線事故都和輸電導線氣動力失穩有關[1-5]。通過風洞試驗或現場實測對不同風場條件下的輸電導線氣動阻力系數進行研究具有重要的工程意義。

風洞試驗是研究導線平均風荷載阻力系數較成熟和可靠的方法[6-7]。Scruton與Rogers指出，不同粗糙度表面圓柱體阻力系數維持在1.2左右，雷諾數達到臨界域，阻力系數變小[8]。Wardlaw等學者研究了分裂導線阻力系數隨風向角變化的規律[9]。我國學者對于輸電導線的氣動力特性也有一些研究，如李萬平[10]、王昕[11]等。同濟大學的謝強等應用8分裂導線風洞試驗測定了導線阻力系數[12]，并與國內外規范[13-14]取值進行對比。

我國現行架空線路送電技術規范規定：導線或地線體型系數ucs在直徑d<17mm時取1.2，直徑d>17mm，則取1.1[13]。國內外現行的規范關于分裂導線風荷載計算方法，都是以單根導線風荷載為基礎，用分裂數乘以單根導線風荷載，得到分裂導線風荷載，沒有考慮導線之間的屏蔽干擾效應，且不考慮不同迎風角度對分裂導線風荷載的影響，導致過高地計算了導線風荷載。

本文對不同風場條件下，單根、4、6和8分裂導線模型的平均風荷載阻力系數進行風洞試驗。通過試驗，分析了雷諾數、尾流干擾及湍流度對導線氣動阻力系數的影響，研究了分裂導線平均風荷載阻力系數隨不同風向角的變化規律，結果表明分裂導線阻力系數并不是按照現行規范方法簡單的單根導線阻力系數乘以分裂數，而是比規范方法要小，這對于導線風荷載合理化設計非常重要。分裂導線平均風荷載阻力系數隨著迎風角度的變化呈現拋物線變化趨勢，依據這一規律，在輸電線路設計時，可以避開導線平均風荷載阻力系數較大的迎風角度，為輸電線路設計的經濟性與合理性提供依據。

1 風洞試驗

1.1 試驗方法介紹

采用能反映實際粗糙度的JL/G1A 630-45、JL/G1A 900-40導線進行風洞試驗。根據導線剛度、天平精度和試驗阻塞比確定模型長度約為100cm，2種模型直徑分別為33.8和39.9mm。在湖南大學HD-2號風洞高速段完成了單根、4、6和8分裂導線風荷載測力實驗。單根導線布置如圖1所示，通過底座將模型固定到天平上，底座上方采用圓板和導流板籠罩著測力天平底座和連接構件以避免固定底座接承受風荷載從而影響測試精度。導線頂部安裝有與導線模型頂端不接觸的(大約5mm間距)端板，由于空隙很小加上端板本身對流體的導流作用，可以克服導線自由端的端部流影響。測試過程中，旋轉轉盤來模擬不同來流風向角，通過測力天平測得導線在不同工況下的風荷載，進而計算得到平均風荷載阻力系數。

圖1 單導線布置

1.2 試驗過程

通過風洞試驗得到2種模型單根導線(如圖1)的風荷載氣動阻力系數和JL/G1A 630-45型號單根導線(見圖2)風荷載氣動阻力系數。圖2中2根導線沿來流中心線上下游布置，通過旋轉轉盤使得下游導線偏離尾流中心線距離為Y，以分析尾流干擾對導線阻力系數影響。

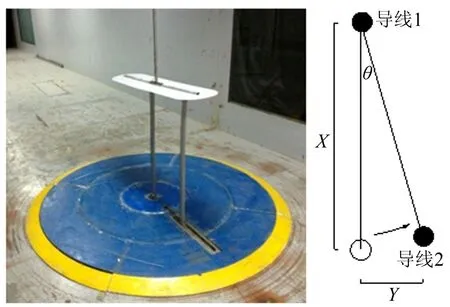
圖2 2根導線布置及干擾導線旋轉示意

Fig.2 Configuration of two conductors and interference conductor rotation

在20和30m/s風速下，分別對JL/G1A 630-45型號4、6和8分裂導線進行測力試驗，如圖3和4所示。分裂導線間隔距離為400mm。通過大型底盤，將4、6和8 分裂導線模型固定在測力天平上，通過轉動轉盤以模擬不同來流方式(見圖3)，以分析分裂導線風荷載阻力系數隨迎風角度的變化。

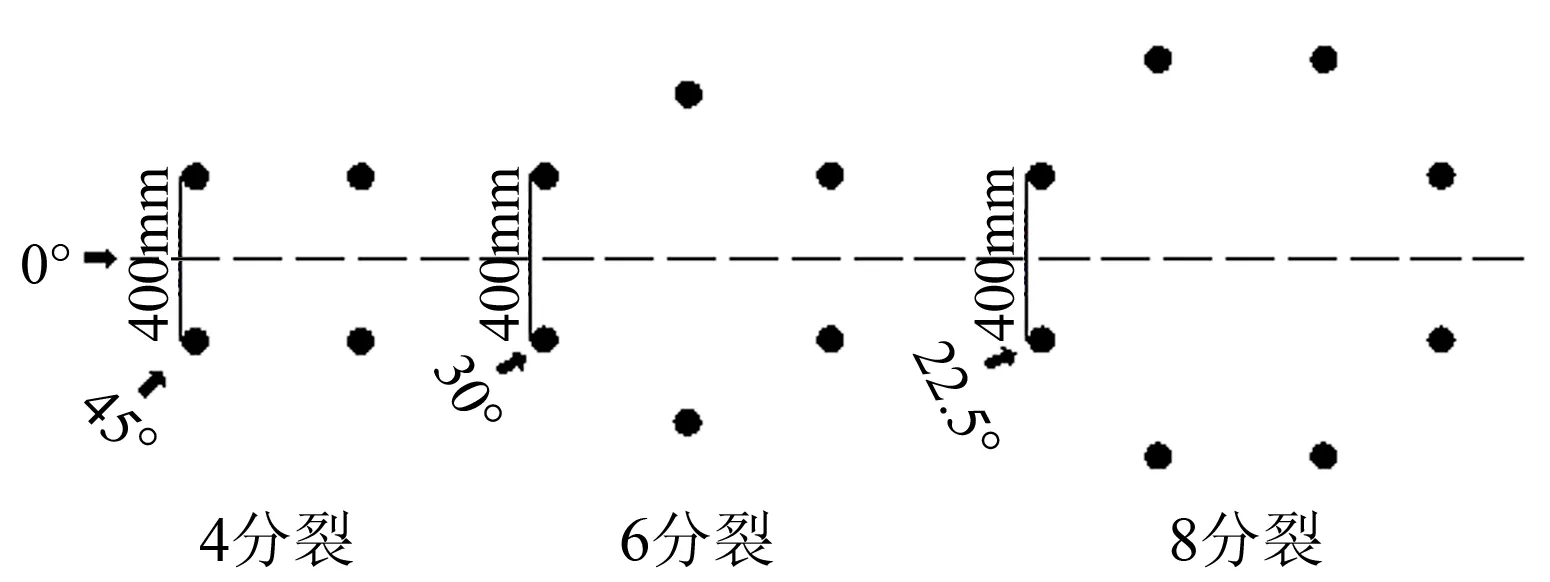
圖3 4分裂、6分裂、8分裂導線布置

Fig.3 Configuration of 4-bundled,6-bundled and 8-bundled conductors

圖4 6分裂導線風洞試驗

2 單導線氣動力特性

2.1 雷諾數效應影響分析

雷諾數為慣性力和粘性力之比，是流場的1個重要參數。流體由層流向湍流過渡的雷諾數，稱為臨界雷諾數Re[15]：

(1)

式中：v=0.15cm2/s ,U為來流風速(m/s)，l為特征長度。與雷諾數有關的參數主要是來流風速和物體的特征尺寸(本文為導線直徑d)。不同風速下2種模型對應的雷諾數如表1所示。

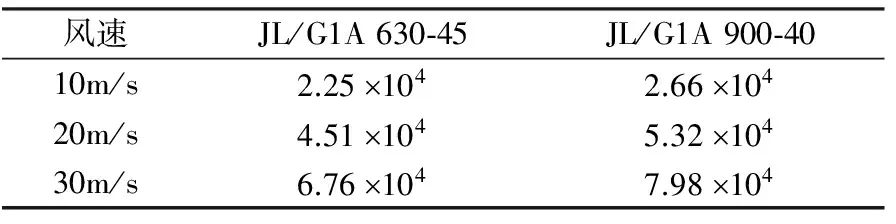
表1 不同試驗風速下2種導線模型雷諾數

通過風洞試驗得到的JL/G1A 630-45和JL/G1A 900-40導線阻力系數如表2所示。圖5給出了本文結果和Wardlaw等[9]的結果對比。圖5表明，導線的表面粗糙度使雷諾數臨界區由105提前至104量級。10m/s風速時導線阻力系數為1.0左右，正好位于雷諾數臨界區；20m/s風速時導線處于超臨界雷諾數范圍內，導線阻力系數變小為0.8，在超臨界雷諾數范圍內，阻力系數隨雷諾數增加而增加。因此，30m/s時對應的阻力系數比20m/s時要大。

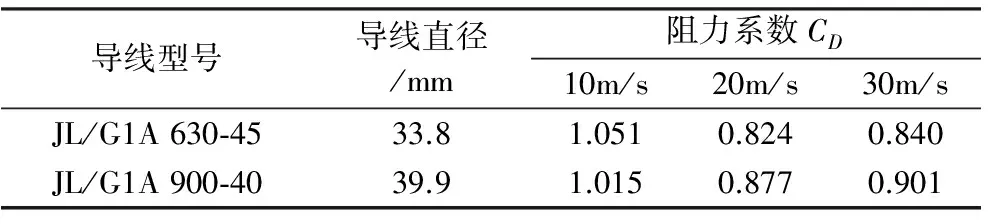
表2 不同型號單導線阻力系數(均勻流)

2.2 尾流效應影響分析

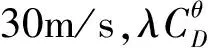
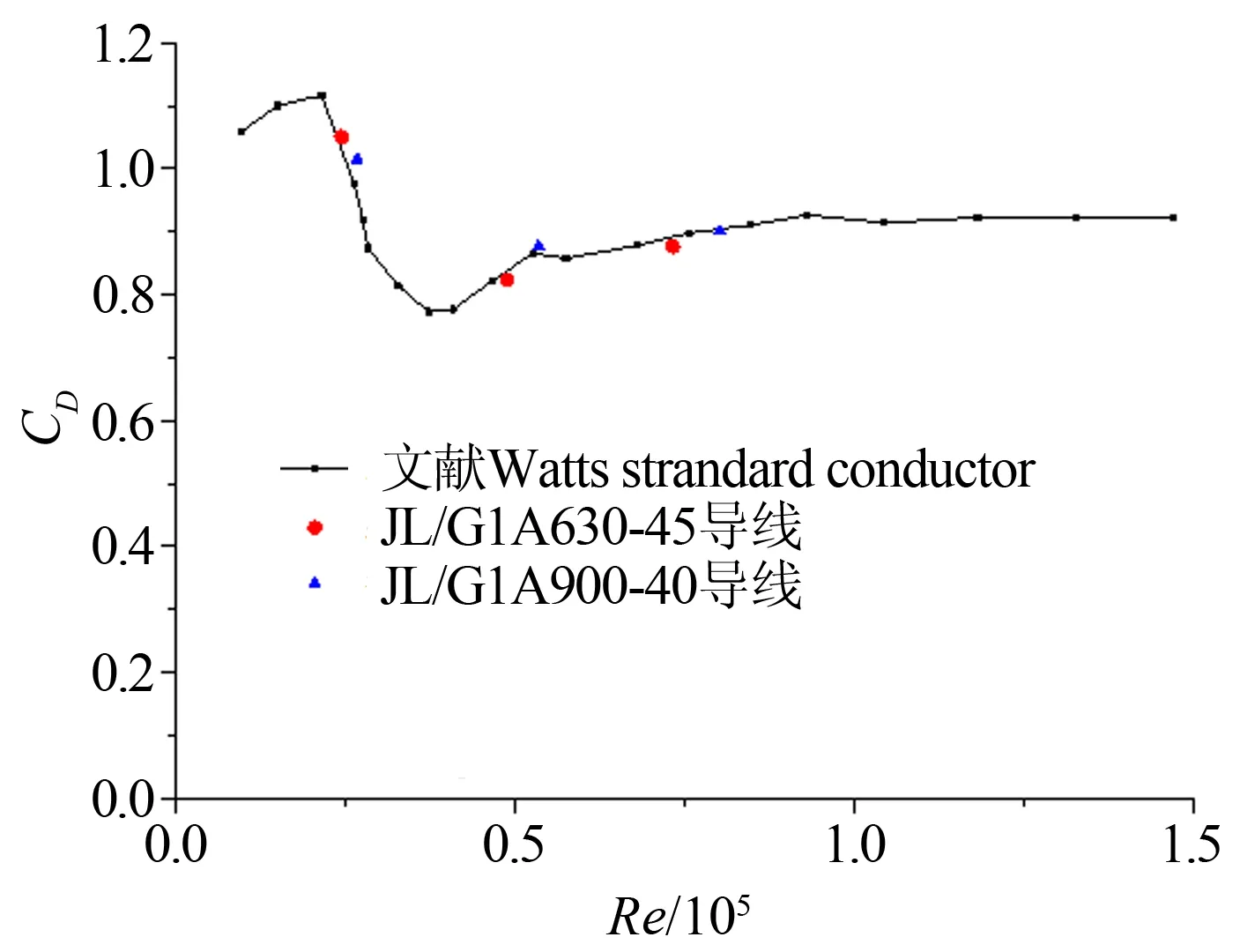
圖5 不同風速下單導線阻力系數曲線(均勻流)

Fig.5 Drag coefficient curve of single conductor under different wind speed (uniform flow)

從表3和圖6可見，阻力系數隨Y/d(d為導線直徑，33.8mm)的增大呈現增大的趨勢。2根導線沿尾流中心線方向布置時，平均風荷載阻力系數最小，增大到一定的距離后，和無干擾單根導線平均風荷載阻力系數基本一致，這是因為干擾偏移距離Y增大，上游導線的遮擋效應明顯減小，下游導線受到的風荷載作用逐漸加強。尾流干擾對導線阻力系數影響較明顯，在2分裂導線線路設計時，應保持導線中心線方向和主導風向一致。

表3 不同位置尾流干擾阻力系數(均勻流)

2.3 湍流度效應影響分析

采用格柵湍流進行湍流工況下導線風荷載測力試驗，格柵以及導線的安裝如圖7所示。通過調節葉柵之間的距離和迎風角得到需要的湍流度，格柵沿風洞中心線對稱安裝，以保證多分裂導線模型范圍內湍流度和風速的均勻性。調試的湍流度為10.7%，接近試驗所需要的10%。

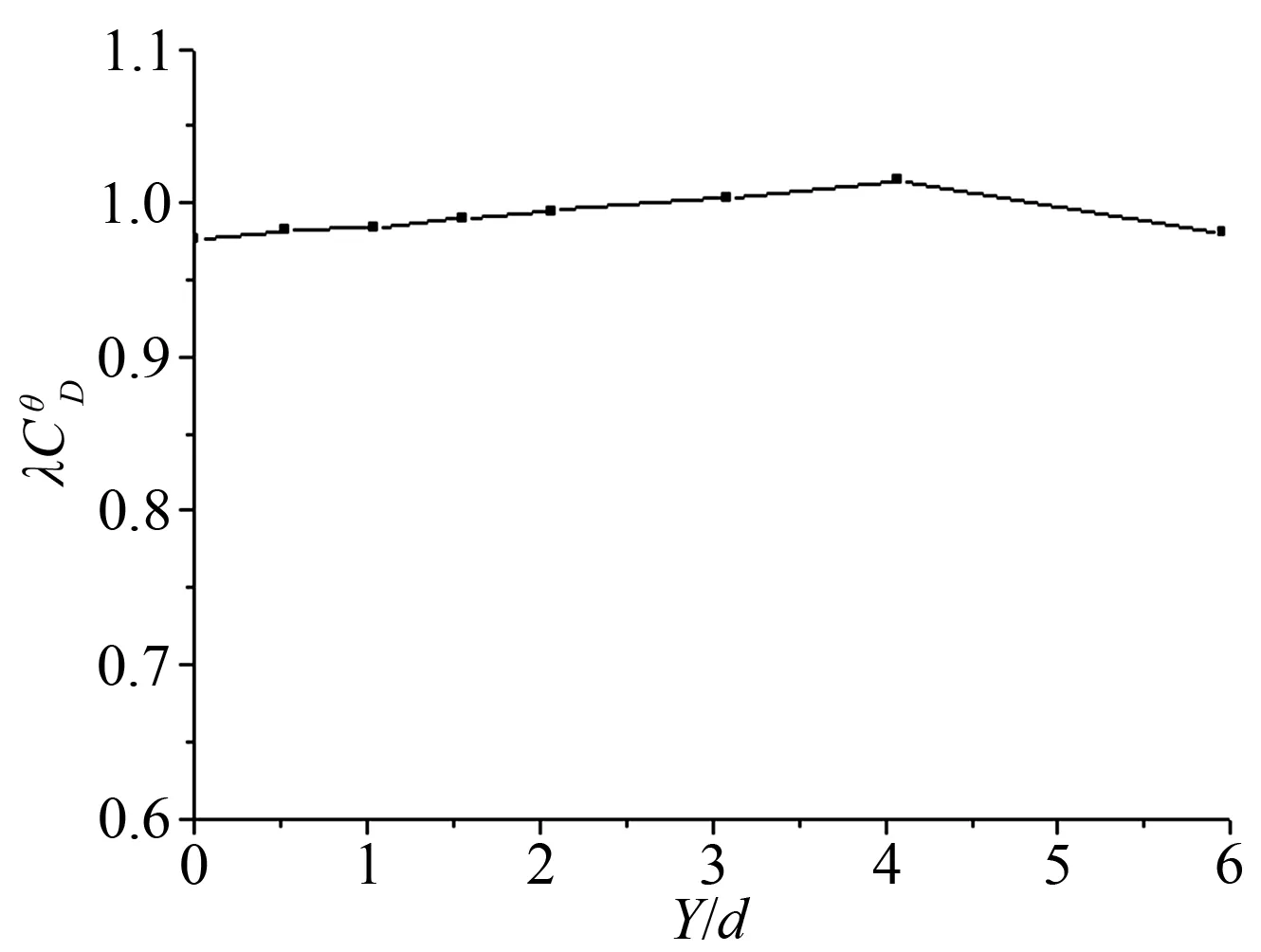
圖6 不同位置尾流干擾阻力系數

圖7 單導線風洞試驗(湍流場)

對JL/G1A 630-45型單根導線的阻力系數進行測試，考慮到格柵的擋風面積較大，為保證試驗的安全性，湍流場的試驗風速為10和20m/s，導線風荷載阻力系數如表5所示。

表5 不同風速下單根導線阻力系數值(湍流場)

現有文獻中，湍流場與均勻流下的測力試驗結果并不一致。有些研究成果認為湍流場下的力系數更大[6]，而有些研究成果得到的湍流場下的力系數值則更小[8]。這是因為湍流場的影響因素很多，比如相同湍流度下的風場其流場功率譜、積分尺度和壓力相關性可能不相同，從而導致相同湍流度下的測力結果存在一定偏差。

通過風洞試驗，本文對湍流場和均勻流場下的單根導線阻力系數進行對比。結果表明，在10%湍流度下單根導線的阻力系數均比均勻流場下的偏大約5%～15%左右?？紤]到湍流場中導線表面壓力的相關性比實際導線更強，因此可以認為湍流場下的阻力系數比均勻流下增大約10%。

3 分裂導線干擾效應研究

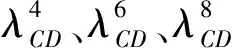
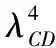
表6 4分裂導線和單導線阻力系數比值

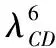
表7 6分裂導線阻力系數和

圖8～10可以看出，多分裂導線風荷載平均阻力系數呈現類似拋物線變化趨勢，在某個迎風角度下，阻力系數將出現最大值，這個風向角對建立導線風荷載模型是不利的。在輸電線路抗風設計時，選擇角迎風方式或者邊迎風方式比其它角度迎風方式更加合理和經濟。

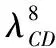
表8 8分裂導線CD以及比值

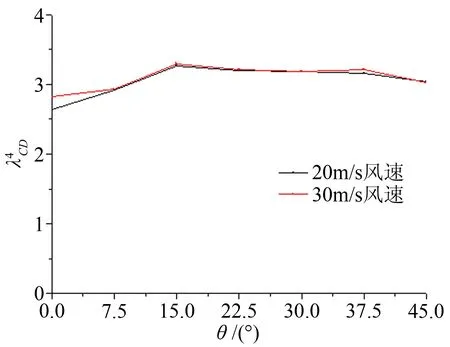
圖8 4分裂導線和單導線CD比值

Fig.8 Drag coefficient ratio of 4-bundled conductors to single conductor

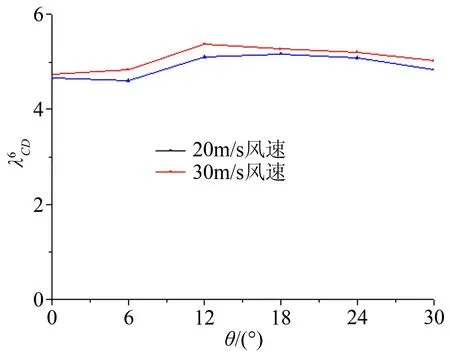
圖9 6分裂導線CD以及比值

Fig.9 Drag coefficient ratio of 6-bundled conductors to single conductor

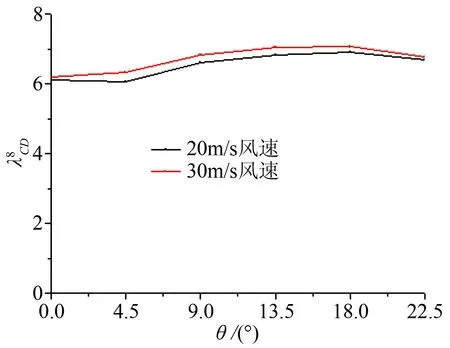
圖10 8分裂導線CD以及比值

Fig.10 Drag coefficient ratio of 8-bundled conductors to single conductor

4 結 論

通過風洞試驗研究了特高壓輸電線平均風荷載阻力系數，分析了導線平均風荷載阻力系數的影響因素，討論了多分裂導線氣動干擾性屏蔽效應。可以得出以下結論：

(1) 雷諾數對導線阻力系數影響比較大，導線表面的粗糙度使得雷諾數臨界區提前至104數量級。中上游導線尾流引起的干擾屏蔽效應使得分裂導線總體風荷載降低，對于雙分裂導線，導線串列布置時阻力系數最小；

(2) 多分裂導線相互干擾及屏蔽效應明顯?，F行規范以單根導線阻力系數乘以相應的分裂數取值是不合理的。設計過程中可以通過風洞試驗或者乘以一個折減系數得到分裂導線平均風荷載阻力系數，以增加輸電線路風荷載設計的經濟合理性；

(3) 不同迎風角度對多分裂導線阻力系數的影響較大，最大可以達到20%以上, 對于正多邊形布置的分裂導線，平均風荷載阻力系數隨迎風角度呈現拋物線的變化趨勢。因此，在輸電線路設計中，選擇角迎風或者邊迎風方式，對控制輸電線的風荷載及風振響應更為有利。

[1] 汪秀麗. 特高壓輸電技術的發展[J]. 水利電力科技, 2006, 32(2): 6-16.

[2] 項立人. 應該加快我國特高壓輸電前期工作的研究[J]. 電網技術, 1996, 20(2): 54-58.

Xiang Liren. Speed up earlier UHV transmission research in china[J]. Power System Technology, 1996, 20(2): 54-58.

[3] 楊靖波, 李正, 楊風利, 等. 2008 年電網冰災覆冰及倒塔特征分析[J]. 電網與水力發電進展, 2008, 24(4): 4-8.

Yang Jingbo, Li Zheng, Yang Fengli, et al. Analysis of the features of covered ice and collapsed tower of transmission line snow and ice attacked in 2008[J]. Advances of Power System & Hydroelectric Engineering, 2008, 24(4): 4-8.

[4] 謝強, 李杰. 電力系統自然災害的現狀與對策[J]. 自然災害學報, 2006, 15(4): 126-131.

Xie Qiang, Li Jie. Current situation of natural disaster in electric power system and counter measures[J]. Journal of Natural Disasters, 2006, 15(2): 126-131.

[5] Loredo-Souza A M, Davenport A G. The effects of high winds on transmission lines[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74: 987-994.

[6] Basu R I. Aerodynamic forces on structures of circular cross-section. Part 1. Model-scale data obtained under two-dimensional conditions in low-turbulence streams[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1985, 21(3): 273-294.

[7] Basu R I. Aerodynamic forces on structures of circular cross-section. Part 2. The influence of turbulence and three-dimensional effects[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1986, 24(1): 33-59.

[8] Scruton C, Rogers E W E, Menzies J B, et al. Steady and unsteady wind loading of buildings and structures [and discussion][J]. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 1971, 269(1199): 353-383.

[9] Wardlaw R L, Cooper K R, Ko R G, et al. Wind tunnel and analytical investigations into the aeroelastic behaviour of bundled conductors[J]. Power Apparatus and Systems, IEEE Transactions on, 1975, 94(2): 642-654.

[10] 李萬平, 楊新祥. 覆冰導線群的靜氣動力特性[J]. 空氣動力學學報, 1995, 13(4): 427-434.

Li Wanping, Yang Xinxiang. Static aerodynamic characteristics of iced conductor group[J]. Acta Aerodynamica Sinica, 1995, 13(4): 427-434.

[11] 王昕. 覆冰導線舞動風洞試驗研究及輸電塔線體系舞動模擬[D]. 浙江大學, 2011.

Wang Xi. Wind tunnel test on galloping iced conductors and galloping simulation for transmission tower-line system[D]. Zhejiang University, 2011.

[12] 謝強, 謝超, 管政. 特高壓8分裂導線風荷載干擾效應風洞試驗[J]. 高電壓技術, 2011, 37(9): 2126-2132.

Xie Qiang, Xie Chao, Guan Zheng. Wind tunnel test on the interference effect on wind load of UHV 8-bundled conductors[J]. High Voltage Engineering, 37(9): 2126-2132.

[13] 中國電力企業聯合會. GB50545-2010 110kV-750kV 架空輸電塔線路設計規范[S]. 北京: 中國計劃出版社, 2010.

[14] American Society of Civil Engineers. Guidelines for electrical transmission line structural loading[S]. Reston, USA: ASCE, 2010.

[15] 陳政清. 橋梁風工程[M]. 北京: 人民交通出版社, 2000.

(編輯：李金勇)

Research on interference effects of wind load on bundled conductors

Zuo Taihui1, Niu Huawei2, Min Xuan3, Hua Xugang2

(1. Guangdong Povincial Academy of Building Research Group Co., LTD, Guangzhou 510050,China; 2. Wind Engineering Research Center of Hunan University, Changsha 410082, China; 3. China State Gird Electric Power Research Institute, Wuhan 430074, China)

It is important to take into account the drag coefficient and interference shielding effect under different wind conditions in the design of bundled conductors. However, it is a complex problem under different wind angles and Reynolds numbers conditions. In this paper, wind tunnel test on a sectional conductor model with 1m long and 1:30 aspect ratio was firstly conducted to investigate the influence of Reynolds number and wake effect on the mean drag coefficient of bundled conductors. Then, sectional model tests of 4-, 6- and 8-bundled conductors under different wind attack angles and velocities in the uniform flow were conducted to analyze the shielding effect of drag coefficient of bundled conductors. The results indicate that the interference shielding effect is evident for multi-bundled conductors. In addition, the variation of the wind attack angle has great effect on the wind loads, the values of which are obviously smaller than that of the current design specification. Therefore, it is of great importance to pay attention to the influence of the wind attack angle and interference shielding on the wind load computation in the design of bundled conductors.

wind load;aerodynamic drag coefficient;bundled conductors;wind tunnel test;interference shielding effect

1672-9897(2015)02-0037-06

10.11729/syltlx20140060

2014-05-22;

2014-08-07

ZuoTH,NiuHW,MinX,etal.Researchoninterferenceeffectsofwindloadonbundledconductors.JournalofExperimentsinFluidMechanics, 2015, 29(2): 37-42. 左太輝, 牛華偉, 閔 絢, 等. 分裂導線平均風荷載阻力系數干擾效應研究. 實驗流體力學, 2015, 29(2): 37-42.

TU311.3

A

左太輝(1987-)，男，碩士，助理工程師。研究方向：建筑物、輸電塔、橋梁結構抗風研究。通信地址：廣東省廣州市天河區先烈東路121號廣東省建筑科學研究院(510050)。E-mail: hnhythzuo@163.com

*通信作者 E-mail: hnhythzuo@163.com