弧齒錐齒輪有限元建模與接觸分析
侯祥穎,方宗德,鄧效忠,蔡香偉,寧程豐
(1.西北工業(yè)大學(xué)機(jī)電學(xué)院,陜西西安710072;2.河南科技大學(xué)機(jī)電工程學(xué)院,河南洛陽471023)
弧齒錐齒輪有限元建模與接觸分析
侯祥穎1,方宗德1,鄧效忠2,蔡香偉1,寧程豐1
(1.西北工業(yè)大學(xué)機(jī)電學(xué)院,陜西西安710072;2.河南科技大學(xué)機(jī)電工程學(xué)院,河南洛陽471023)
為了使有限元軟件能夠?qū)X面微米量級變化的齒輪進(jìn)行分析,提出了基于高精度建模的有限元分析方法。將齒面的理論計算公式轉(zhuǎn)化成數(shù)值計算算法,按照有限元理論和有限元軟件的編程語法將齒輪實體進(jìn)行節(jié)點坐標(biāo)求解和網(wǎng)格單元劃分,可以求得一對裝配好的有限元齒輪模型。高精度建模的高重合度弧齒錐齒輪算例中,將有限元計算結(jié)果與實驗結(jié)果對比,發(fā)現(xiàn)兩者的一致性:彎曲應(yīng)力曲線形狀一致,變化規(guī)律相近;接觸印痕區(qū)域一致,變化趨勢相同。高精度建模有限元分析能夠清晰的反映齒面微米量級改變導(dǎo)致的印痕和應(yīng)力的變化。
弧齒錐齒輪;有限元;接觸分析;彎曲應(yīng)力;接觸印痕
弧齒錐齒輪是一種不完全共軛局部點接觸的齒輪副,齒面形狀和加工機(jī)床的調(diào)整都比較復(fù)雜。目前國外已經(jīng)較多地將弧齒錐齒輪應(yīng)用于船艦傳動系統(tǒng),國內(nèi)在船艦上的應(yīng)用相對較少,這方面的研究正在進(jìn)行。弧齒錐齒輪傳動平穩(wěn),是動力傳輸?shù)年P(guān)鍵部件,在強(qiáng)度、動態(tài)性能與可靠性方面等方面都有很高的要求。鄧效忠等[1]曾提出高重合度弧齒錐齒輪的設(shè)計方法,采用LTCA理論,通過有限元應(yīng)力影響矩陣法對其相關(guān)性能進(jìn)行了詳細(xì)討論[2]。高重合度弧齒錐齒輪是通過齒面修形改善其嚙合性能的典型,不同的弧齒錐齒輪齒面精度會使弧齒錐齒輪有不同的傳動性能。本文以一對高重合度弧齒錐齒輪為例,通過高精度齒面建模和裝配,導(dǎo)入有限元分析軟件分析,并與實驗結(jié)果進(jìn)行了對比驗證分析。
1 高重合度弧齒錐齒輪
文獻(xiàn)[3?5]等利用NURBS曲面函數(shù)對齒面進(jìn)行重構(gòu)來建立弧齒錐齒輪模型。但是此方法計算求得模型的齒面與理論齒面仍有一定誤差;在對一對齒輪進(jìn)行有限元接觸分析時,采用手動裝配,可能存在干涉和裝配誤差等現(xiàn)象,產(chǎn)生計算誤差或錯誤。對于齒面修形處于微米量級的齒輪來說,上述方法建模精度遠(yuǎn)遠(yuǎn)達(dá)不到要求。采用曲面擬合方法的誤差分布如圖1所示,誤差可能達(dá)到十幾甚至幾十微米,且有很大隨機(jī)性,分布不均勻;而且此方法需要進(jìn)行三維建模,然后再將模型導(dǎo)入有限元軟件進(jìn)行實體分割、網(wǎng)格劃分等操作,工作量大,可重復(fù)性差。
在保證齒輪基本參數(shù)(如表1所示)不變的條件下,采用局部綜合法使接觸路徑傾斜和改變齒面的失配量,設(shè)計了3種重合度不同的弧齒錐齒輪。(詳見文獻(xiàn)[2])高重合度設(shè)計方法不改變齒輪輪坯基本參數(shù),只對小輪齒面加工參數(shù)進(jìn)行調(diào)整,而保持大輪的加工參數(shù)不變,通過小輪齒面的改變使接觸路徑傾斜,接觸路徑延長,以達(dá)到增大重合度的目的。小輪齒面的修形量往往只有十幾微米甚至幾微米,故要求有限元模型要有極高的精度才能反映出齒面變化的影響。

圖1 NURBS曲面重構(gòu)誤差分析Fig.1 Error analysis of NURBS surface reconstruction
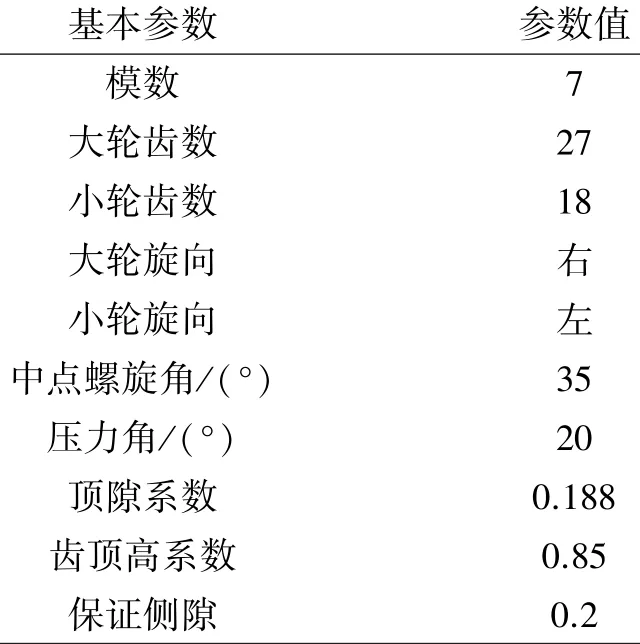
表1 弧齒錐齒輪參數(shù)Table 1 Basic parameters of spiral bevel gear
本文算例采取的傾斜角分別為20°、50°、80°接觸路徑,通過TCA分析得到傳動誤差如圖2所示,圖2(a)理論設(shè)計重合度只有1.25左右,圖2(b)理論設(shè)計重合度增加至1.75左右,圖2(c)理論設(shè)計重合度增加至2.0以上,傳動誤差曲線明顯可以看出存在三齒嚙合區(qū)。


圖2 3種不同齒輪的傳動誤差Fig.2 Transmission error of three different designs
2 弧齒錐齒輪有限元模型建立
2.1 通過數(shù)值計算求解有限元模型
弧齒錐齒輪齒面較為為復(fù)雜,其加工原理和方法繁瑣,加工參數(shù)較多,一般很難得到齒面方程的解析表達(dá)式,多采用數(shù)值計算的方法,求得齒面上離散的點,即可用離散點構(gòu)建有限元模型[4?5]。
將刀具切削面方程從刀具坐標(biāo)系變換到輪坯坐標(biāo)系下,聯(lián)立齒面的位矢方程和嚙合方程如下(文獻(xiàn)[6]):
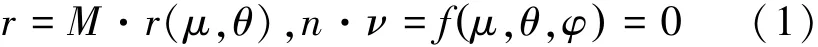
式中:M為刀具坐標(biāo)系到輪坯坐標(biāo)系的變換矩陣,r為刀盤方程,μ、θ分別為切削刃產(chǎn)生圓錐曲面坐標(biāo),φ為轉(zhuǎn)角,n、v分別為齒面點法矢和相對速度矢。由式(1)通過編程進(jìn)行數(shù)值計算,可得出齒面上的離散點在輪坯坐標(biāo)系下的坐標(biāo)。
按照有限元軟件ABAQUS對單元網(wǎng)格以及節(jié)點的書寫語法要求,首先計算理論齒面上的點,將齒面點坐標(biāo)繞軸線旋轉(zhuǎn),對兩齒面之間采用點陣進(jìn)行填充,然后對所有節(jié)點按照一定順序進(jìn)行自然數(shù)編號;之后按順序編寫8節(jié)點單元,單元由8個節(jié)點自然序號構(gòu)成,故點陣的密度決定了網(wǎng)格單元的密度。
裝配時,選取大輪接觸跡線與齒頂線的交點為嚙合參考點,即恰好進(jìn)入嚙合的位置。利用輪齒接觸分析求得嚙合點的坐標(biāo)以及小、大輪對應(yīng)的轉(zhuǎn)角φ1、φ2(式(2)),采用坐標(biāo)轉(zhuǎn)換矩陣,對大小輪分別旋轉(zhuǎn)φ1、φ2,即能通過理論計算完成一對弧齒錐齒輪的裝配。

式中:下標(biāo)1、2分別表示大小齒輪,下標(biāo)p、g分別表示大小輪的齒面參數(shù),上標(biāo)h表示在固定坐標(biāo)系Sh下,分別表示齒面離散點位矢在旋轉(zhuǎn)投影面上的X、Y坐標(biāo),ha2表示大輪齒頂高,AFO表示外錐距,γ2為大輪根錐角。
通過編寫inp文件將裝配坐標(biāo)系下大小輪的節(jié)點和單元數(shù)據(jù)導(dǎo)入ABAQUS軟件中,可直接得到有限元裝配模型(如圖3所示)。

圖3 有限元裝配模型Fig.3 Assembly model of finite element
2.2 有限元模型前處理
進(jìn)行有限元齒輪接觸分析,單元一般采用六面體一次減縮積分單元(C3D8R),單元屬性在編寫inp文件生成有限元模型時定義(文獻(xiàn)[7]);將已建好的弧齒錐齒輪的五齒有限元模型導(dǎo)入ABAQUS軟件中,需要進(jìn)行以下設(shè)置(文獻(xiàn)[5,8]):
1)定義材料:將大小輪賦予相同的材料屬性,其彈性模量為2.06×105MPa,泊松比為0.3,密度為7.8×10-9t/mm3。
2)定義接觸對:分別將大小輪的齒面、過渡曲面、齒頂?shù)刃纬傻倪B續(xù)面選中,并將此兩對連續(xù)面設(shè)置為接觸對。在接觸屬性中,采用無摩擦硬接觸,計算方法采用Kinematic接觸方法。
3)設(shè)置參考點:取軸線上任一點為參考點,并在參考點和小輪內(nèi)圈和剖面間建立耦合剛體約束。
4)分析類型的定義:采用顯示動力學(xué)分析算法,設(shè)置分析時間并根據(jù)網(wǎng)格數(shù)量選擇適當(dāng)?shù)馁|(zhì)量放大系數(shù)。顯式算法基于動力學(xué)方程,無需迭代,有較好的穩(wěn)定性。
5)場變量和歷史變量設(shè)置:設(shè)置接觸壓強(qiáng)、接觸力、應(yīng)力、位移等為場變量輸出量,動能、內(nèi)能為歷史變量輸出量。
6)邊界條件和載荷:大小輪分別只釋放繞自身軸線旋轉(zhuǎn)的自由度,施加小輪的繞軸線的轉(zhuǎn)速為0.2 rad/s,大輪施加阻力矩為7.5×105N·mm,小輪轉(zhuǎn)速和大輪轉(zhuǎn)矩均采用平緩加載方式;從而模擬出以小輪驅(qū)動大輪,同時小輪受到大輪的阻力矩的作用,在齒面上產(chǎn)生壓力的工況。
同樣將以上設(shè)置步驟編寫入inp文件中,這樣inp文件就包括了所有模型信息和條件設(shè)置信息。直接將inp文件導(dǎo)入ABAQUS中,提交計算即可,無需再人工操作。
3 結(jié)果分析
3.1 有限元仿真結(jié)果
前處理結(jié)束后,用ABAQUS軟件分析可得到弧齒錐齒輪的有限元分析結(jié)果。圖4為某一時刻的小輪凹面和大輪凸面(工作面)的Mises應(yīng)力云圖,圖中可以看到3對齒輪同時嚙合的狀態(tài)。

圖4 有限元計算Misse應(yīng)力云圖Fig.4 Mises stress nephogram of finite element calculation
改變運(yùn)動時間,當(dāng)給小輪施加逆時針轉(zhuǎn)速時,小輪的凹面和大輪凸面發(fā)生接觸,小輪驅(qū)動大輪順時針旋轉(zhuǎn),同時大輪的阻力矩模擬負(fù)載,使兩齒嚙合點處產(chǎn)生應(yīng)力和變形。小輪凹面接觸橢圓從大端齒根逐漸向小端齒頂移動,大輪凸面接觸區(qū)域接觸橢圓從大端齒頂逐漸向小端齒根移動;最大主應(yīng)力位于接觸橢圓區(qū)域的中心,接觸橢圓在齒面中間面積最大,表示在齒面中間輪齒承受載荷最大。
3.2 高重合度對齒面接觸力的影響
有限元計算結(jié)束生成結(jié)果文件,對運(yùn)行編譯好的腳本文件,從計算結(jié)果模型中提取所需要的節(jié)點坐標(biāo),接觸壓強(qiáng)和Mises應(yīng)力等,并通過數(shù)據(jù)處理軟件將應(yīng)力曲線繪出,如圖5所示。

圖5 3種接觸路徑的接觸應(yīng)力對比Fig.5 Contrast of contact stress with three different designs
通過對比容易發(fā)現(xiàn),在計算載荷一定的情況下(大輪扭矩7.5×105N·mm),接觸路徑傾斜度越大,即傾斜角越小,則重合度越大,接觸應(yīng)力越小。傾斜角80°設(shè)計中接觸應(yīng)力最大值為1 111.84 MPa,而傾斜角20°設(shè)計中的最大值為1 164.98 MPa;接觸路徑傾斜前后相比,接觸應(yīng)力下降4.56%,并且,隨著接觸路徑的傾斜,重合度的增大,齒面接觸應(yīng)力變化趨于平緩,曲線上升下降都明顯變化緩慢,即加載明顯趨于平穩(wěn)。
4 彎曲應(yīng)力實驗對比
本實驗由調(diào)頻電機(jī)(30 kW)提供實驗驅(qū)動力,經(jīng)減速器減速,利用轉(zhuǎn)矩轉(zhuǎn)速傳感器將動力輸給試驗齒輪小輪;試驗齒輪由磁粉制動器施加負(fù)荷,裝配在試驗箱內(nèi)。通過測量齒根應(yīng)變獲得齒根彎曲應(yīng)力,通過轉(zhuǎn)矩轉(zhuǎn)速測試儀測得試驗齒輪的轉(zhuǎn)矩和轉(zhuǎn)速。電阻應(yīng)變計貼在大輪凸面的齒根中點處,位于非嚙合區(qū),在遠(yuǎn)離嚙合齒面處的齒坯上貼2個溫度補(bǔ)償片,分別與凸面和凹面的應(yīng)變計組成半橋連接。引線由集流環(huán)引出,經(jīng)應(yīng)變儀放大,通過多功能信號測試儀紀(jì)錄[9]。通過實驗測得齒根應(yīng)力測試曲線如圖6所示。圖7為對應(yīng)齒輪的有限元仿真計算所得到的大輪齒根中點彎曲應(yīng)力過程,詳細(xì)數(shù)值比較如表2。通過圖6與圖7以及表2對比,大輪齒根中點應(yīng)力變化過程中,實驗測得波形傾斜角20°設(shè)計最大電壓信號達(dá)1.053 V,而傾斜角80°設(shè)計最大電壓信號0.597 V,二者相比峰值下降43.3%;有限元分析結(jié)果中,傾斜角20°設(shè)計最大彎曲應(yīng)力為126.08 MPa,而傾斜角80°設(shè)計最大彎曲應(yīng)力值僅為83.28 MPa;接觸路徑傾斜前后相比,彎曲應(yīng)力下降34%,且當(dāng)接觸路徑越傾斜時,即重合度增大,彎曲應(yīng)力數(shù)值明顯下降。隨著接觸路徑傾斜角加大,接觸路徑延伸增長,齒根彎曲應(yīng)力逐漸降低,變化趨于平緩,仿真結(jié)果與實驗結(jié)果曲線變化規(guī)律一致,形狀近似。實驗數(shù)據(jù)與有限元分析結(jié)果有一定的誤差,誤差的主要來源有:實驗儀器條件,實驗系統(tǒng)誤差,應(yīng)變計所貼位置,溫度補(bǔ)償片的選用;有限元所選用的單元類型、網(wǎng)格密度、計算方法、質(zhì)量放大系數(shù)等。
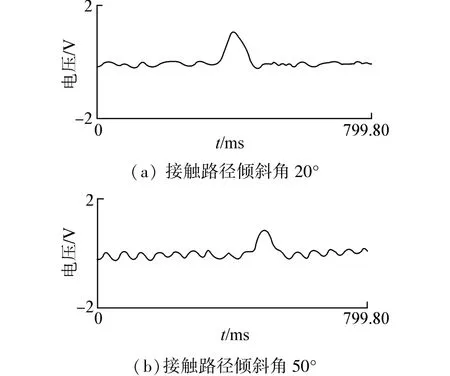

圖6 三對齒輪齒根應(yīng)力測定曲線Fig.6 Bending stress curves of experiment results
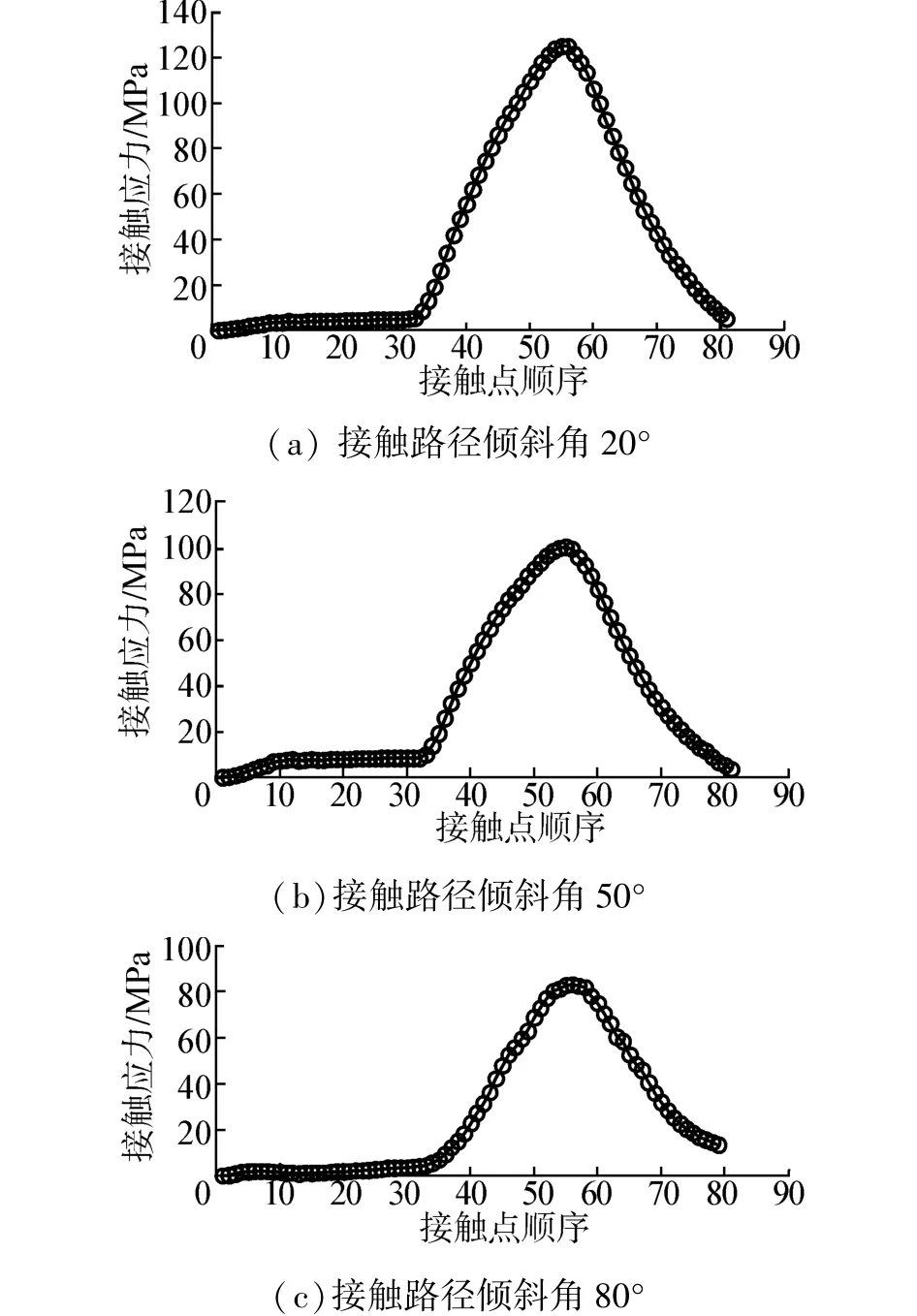
圖7 有限元大輪齒根中點彎曲應(yīng)力過程Fig.7 Bending stress changes of midpoint on gear root

表2 大輪齒根應(yīng)力實驗數(shù)據(jù)與有限元分析比較Table 2 Bending stress comparison between experi?ment results and finite element analysis
5 接觸印痕實驗對比
有限元分析結(jié)束后,編寫讀取abaqus結(jié)果文件(.odb文件)的腳本文件,求得某齒一個嚙合周期內(nèi)每一瞬時的接觸區(qū)域內(nèi)的點坐標(biāo),利用數(shù)據(jù)處理軟件編程,將所有點疊加到同一坐標(biāo)系下,并將其投影到旋轉(zhuǎn)投影面,即得到有限元分析的接觸印痕區(qū)域。有限元計算和實驗得到接觸印痕區(qū)域分別如圖8和圖9所示。
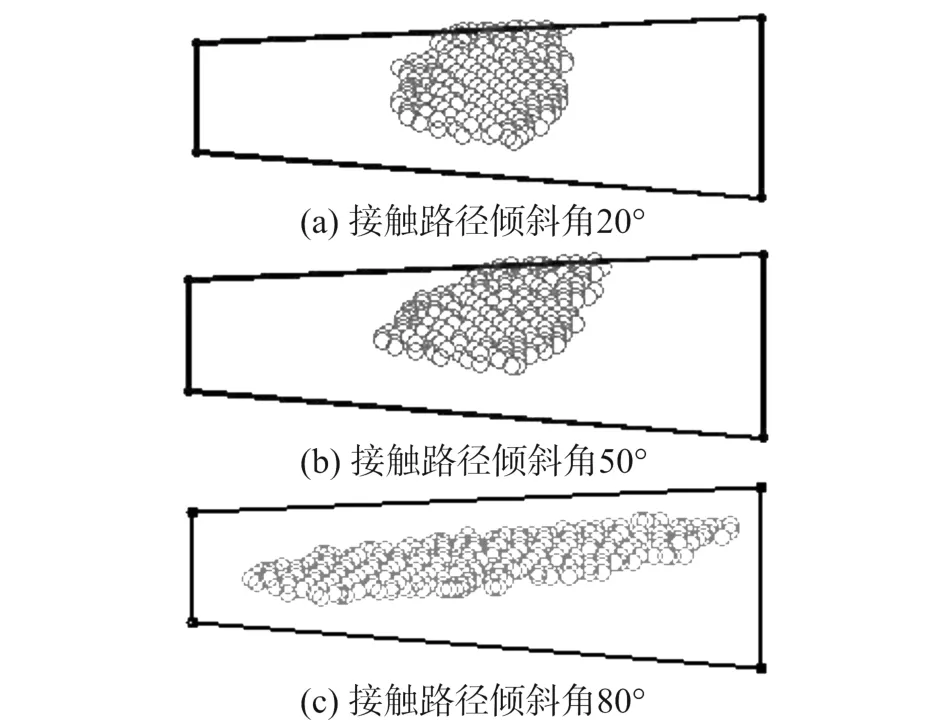
圖8 有限元印痕提取Fig.8 Contact pattern of finite element analysis

圖9 實驗印痕Fig.9 Contact pattern of experiment
通過對比圖8和圖9,隨著傾斜度逐漸變大,接觸區(qū)域傾斜,接觸路徑增長,接觸橢圓長軸變短,有限元計算結(jié)果與實驗結(jié)果印痕區(qū)域一致,變化規(guī)律相同,由此證明此高精度建模方法及有限元分析方法的正確性。
6 結(jié)論
1)本文有限元建模采用數(shù)值計算的方法,得到節(jié)點坐標(biāo),并通過編號導(dǎo)入inp文件中直接建立有限元模型,省去了三維建模以及劃分網(wǎng)格的過程,通過與NURBS曲面重構(gòu)結(jié)果對比,證明此方法有限元齒面精度及裝配精度極高,可重復(fù)性好,適用于高精度的齒輪接觸分析。
2)通過有限元計算與實驗結(jié)果對比,隨著接觸路徑傾斜度逐漸變大,有限元計算印痕接觸路徑逐漸增長,接觸橢圓長軸逐漸變短,印痕區(qū)域和變化規(guī)律與實驗一致;有限元計算齒根彎曲應(yīng)力逐漸降低,變化趨于平緩,與實驗彎曲應(yīng)力變化趨勢一致,形狀近似,驗證了本文方法的計算精度。
[1]鄧效忠,方宗德,張金良等.弧齒錐齒輪的高重合度設(shè)計[J].中國機(jī)械工程,2002,14(19):791?795.DENG Xiaozhong,F(xiàn)ANG Zongde,ZHANG Jinliang,et al.Design of spiral bevel gears with high contact ratio[J].Chi?na Mechanical Engineering,2002,14(19):791?795.
[2]鄧效忠,方宗德,魏冰陽.高重合度弧齒錐齒輪的接觸應(yīng)力與彎曲應(yīng)力分析[C]//中國工程機(jī)械學(xué)會2003年年會論文集,2003:107?111.DENG Xiaozhong,F(xiàn)ANG Zongde,WEI Bingyang.Analysis of contact stress and bending stress on spiral bevel gears of high contact ratio[C]//China Mechanical Engineering Soci?ety 2003 Annual Meeting Proceedings,2003:107?111.
[3]唐進(jìn)元,蒲太平.弧齒錐齒輪動態(tài)嚙合有限元數(shù)值分析[J].機(jī)械科學(xué)與技術(shù),2009,8(8):981?985.TANG Jinyuan,PU Taiping.FEM numerical analysis of the dynamic engagement of spiral bevel gears[J].Mechanical Science and Technology for Aerospace Engineering,2009,8(8):981?985.
[4]ASTOUL J,GENEIX J,MERMOZ E,et al.A simple and robust method for spiral bevel gear generation and tooth con?tact analysis[J].International Journal on Interactive Design and Manufacturing,2013,7(1):37?49.
[5]唐進(jìn)元,蒲太平.基于有限元法的螺旋錐齒輪嚙合剛度計算[J].機(jī)械工程學(xué)報,2011,47(11):23?29.TANG Jinyuan,PU Taiping.Spiral bevel gear meshing stiff?ness calculations based on the finiteelement method[J].Journal of Mechanical Engineering,2011,47(11):23?29.
[6]LITVIN F L.Gear geometry and applied theory[M].Cam?bridge University Press,2004:613?635.
[7]GONZALEZ?PEREZ I,ISERTE J L,F(xiàn)UENTES A.Imple?mentation of Hertz theory and validation of a finite element model for stress analysis of gear drives with localized bearing contact[J].Mechanism and Machine Theory,2011,46(6):765?783.
[8]SHEVELEVA G I,VOLKOV A E,MEDYEDEV V I.Algo?rithms for analysis of meshing and contact of spiral bevel gear[J].Mechanism and Machine Theory,2007,42(2):198?215.
[9]鄧效忠.高重合度弧齒錐齒輪的設(shè)計理論及實驗研究[D].西安:西北工業(yè)大學(xué),2002:49?77.DENG Xiaozhong.Research of design theory and experi?ments on spiral bevel gears with high contact ratio[D].Xi'an:Northwestern Polytechnical University,2002:49?77.
[10]WANG P Y,F(xiàn)AN S C,HUANG Z G.Spiral bevel gear dy?namic contact and tooth impact analysis[J].Journal of Me?chanical Design,2011,133:084501.
[11]GONZALEZ?PEREZ I,RODA?CASANOVA V,F(xiàn)UENTES A,et al.A finite element model for consideration of the tor?sional effect on the bearing contact of gear drives[J].Jour?nal of Mechanical Design,2012,134:071007.
Contact analysis of spiral bevel gears based on finite element model
HOU Xiangying1,F(xiàn)ANG Zongde1,DENG Xiaozhong2,CAI Xiangwei1,NING Chengfeng1
(1.Department of Mechanical Engineering,Northwestern Polytechnical University,Xi'an 710072,China;2.Department of Mechani?cal Engineering,Henan University of Science and Technology,Luoyang 471023,China)
To make analysis on gears whose tooth surfaces have micron level changes,the finite element method based on high?precision finite element model is proposed.The theoretical formulas of tooth surfaces are converted into numerical algorithm,the coordinates of nodes and finite mesh elements of the gears are obtained based on the finite element theory and program syntax of finite element software,and the high?precision finite element model of a pair of gears is built.Through analysis of spiral bevel gears with high contact ratio,the simulation results are in good agreement with the experimental ones.The bending stress curves show the same shape and accordant changing trend,but the contact patterns show the same location and changing trend.The finite element analysis with high?precision modeling could reflect the changes of stresses and contact pattern caused by modification to the surfaces of gears in micron level.
spiral bevel gear;finite element method;contact analysis;bending stress;contact pattern
10.3969/j.issn.1006?7043.201312055
TH132.41
:A
:1006?7043(2015)06?0826?06
http://www.cnki.net/kcms/detail/23.1390.u.20150428.0910.012.html
2013?12?27.網(wǎng)絡(luò)出版時間:2015?04?28.
國家自然科學(xué)基金資助項目(51175423,51375384,51205310).
侯祥穎(1990?),男,博士生;方宗德(1948?),男,教授,博士生導(dǎo)師.
侯祥穎,E?mail:houxiangying@126.com.

