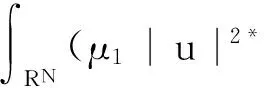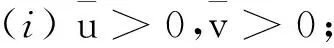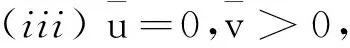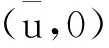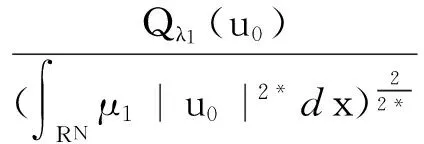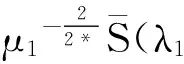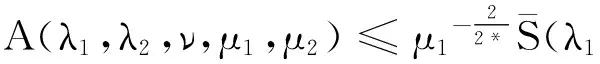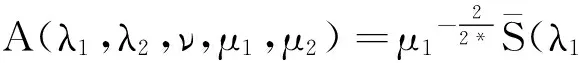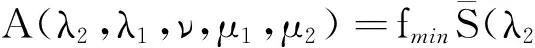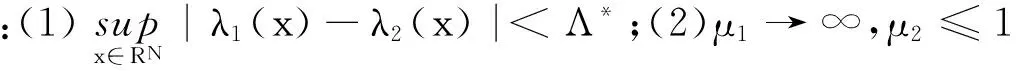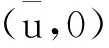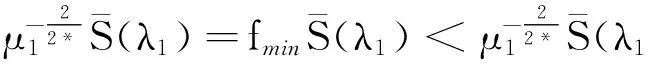帶有不同Hardy位勢和多重Sobolev臨界指數方程組的基態解
康東升, 喻 晶, 上官曉天
(中南民族大學 數學與統計學學院,武漢 430074)
帶有不同Hardy位勢和多重Sobolev臨界指數方程組的基態解
康東升, 喻 晶, 上官曉天
(中南民族大學 數學與統計學學院,武漢 430074)
利用變分方法和分析技巧,研究了帶有多重臨界指標和不同Hardy位勢項的橢圓方程組,證明了方程組基態解的存在性以及瑞利商極小值的可達性.
橢圓方程組;極小值;臨界指數;基態解;變分方法
1 主要問題及主要結果
本文考慮如下橢圓方程組:
(1)

本文主要在積空間D×D中研究問題(1),并且定義其相應的能量泛函為:

μ2|v|2*+ν|u|α|v|β)dx.
那么I∈C1(D×D,R),其對偶積定義如下:
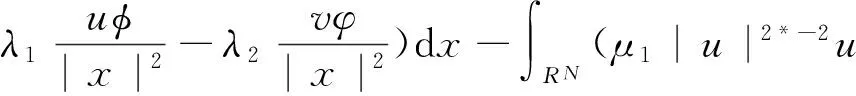
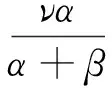
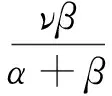
其中u,ν,φ,φ∈D,若(u,v)≠(0,0),I′(u,v),(φ,φ)=0,?(φ,φ)∈D×D,則(u,v)∈D×D被稱為方程組(1)的解,其中I′(u,v)為能量泛函I在點(u,v)處的Fréchet導數.
根據著名的Hardy不等式[1]:
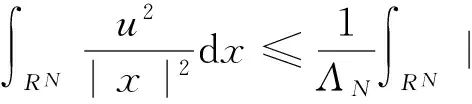
(2)
那么在空間D上等價的范數表示為:
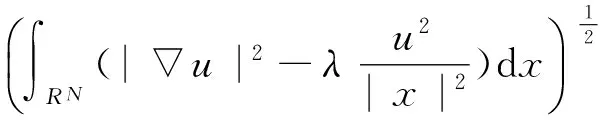
我們可以定義D1,2(RN){0}上的最佳常數:
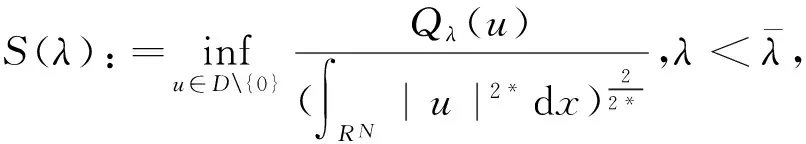
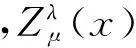
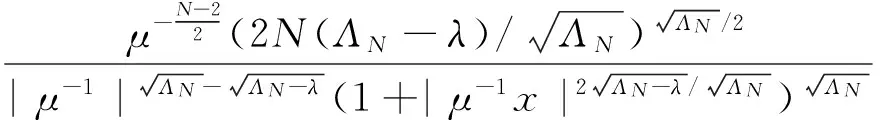
(3)
并且是方程:
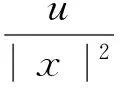
的解.那么(3)式的解滿足:
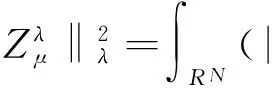
同時在假設(H1)~(H3)下,通過Hardy不等式、Yong不等式和Sobolev不等式定義D1,2(RN){0}2上的最佳常數:
(4)
A=A(λ1,λ2,ν,μ1,μ2):=
(5)
特別地,當ν,λ1,λ2為非負常數時,我們將A寫作B:
B=B(λ1,λ2,ν,μ1,μ2):=
(6)
那么在全文中,我們假設:
(H1) N≥3,N是整數,μ1>0,μ2>0,ν>0,α,β>1,α+β=2*.
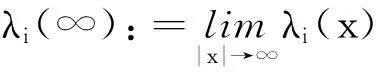
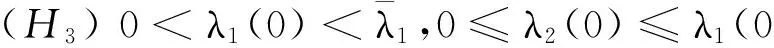
在本文中,在假設(H1)下,定義如下函數:
(7)
其中τmin>0為f(t)在區間(0,+∞)中的最小值點.
在最近幾年,許多學者研究半線性橢圓方程,并且得到了許多研究成果[2-5].特別地,帶有Hardy位勢和Sobolev臨界項的橢圓方程得到了更多學者的關注[6-12].本文將研究方程組(1)的基態解的存在性以及瑞利商的極小值的可達性.
定義1 假設一個方程組所有的解組成的集合為E,如果集合E滿足下面的條件:
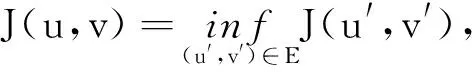
則稱(u,v)∈D×D是該方程組的基態解,即極小能量解.對于本文,在所有可能存在的解中,我們研究方程組(1)的基態解.因為使得方程組相應Rayleigh商取得極小值的解就是原方程組的基態解.
定理1 假設(H1)~(H3)成立,并且N>4,α<2,β<2.
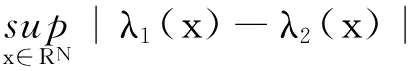
(ii) 如果μ1→∞,μ2≤1,則方程組(1)有正基態解.
(iii) 如果μ1≥1,μ2→0,則方程組(1)有正基態解.
(iv) 存在ν*>0,使得對于所有的ν∈(0,ν*),方程組(1)有正基態解.
下面我們首先證明(1)基態解的存在性;然后證明定理1.為了簡潔起見,我們將省略掉積分號里的“dx”.
2 相關引理
在空間D*=D×D上我們定義能量泛函J(u,v):
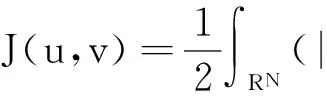
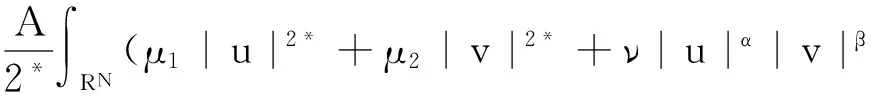
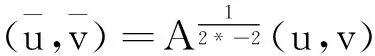
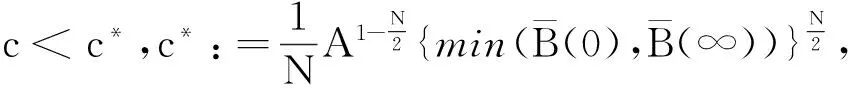
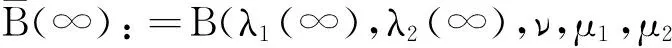
(8)
證明 證明方法與文獻[11]中的引理1.1
類似.
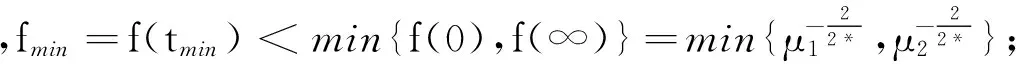
證明 (i)當N>4,α<2,β<2時,

t≥0.
當t→0+,則f′(t)<0并且當t→+∞,f′(t)>0,那么存在tmin≥0使得:
fmin=f(tmin) (ii) 為了證明引理2,引用文獻[9]中定理1的方法,假設w∈D1,2(RN){0}, 那么我們選擇(u,v)=(w,tminw)代入到(5)式中可以得到: A(λi,λi,ν,μ1,μ2). (9) 在(9)式中取w∈D1,2(RN){0}的下界,可以得到: (10) 另一方面,取序列{(u,v)}?D×D為A(λi,λi,ν,μ1,μ2)的最小子列并且定義z=sv, (11) (12) 由Minkowski不等式得: 所以我們可以得到: (13) 通過(10)和(13)式可以推得: 引理3 在假設(H1)~(H3)下,當N>4時,α<2,β<2. (14) (15) A(λ1,λ2,ν,μ1,μ2)≤ (16) 那么當N>4,α<2,β<2,μ1>0,μ2>0,ν>0,α+β=2*時,根據引理2我們將t=tmin帶入到(16)式中: A(λ1,λ2,ν,μ1,μ2) (17) (ii) 如果μ1→∞,μ2≤1,那么(17)式成立. (iii) 如果μ1≥1,μ2→0,那么(17)式成立. J′(un,vn),(φ,φ)=o(‖(φ,φ)‖D×D). 通過引理3可以得到: (18) 再將(u,0)代入到(5)式中我們有: (19) 則通過(18)和(19)式可以得到: (20) 這就表明A(λ1,λ2,ν,μ1,μ2)僅僅只與λ1,μ1有關,與λ2,μ2無關,則從(20)式和引理2可以得到: (21) (22) [1] Hardy G, Littlewood J, Polya G. Inequalities [M].Cambridge: Cambridge University Press, 1988: 239-243. [2] Terracini S. On positive entire solutions to a class of equations with a singular coefficient and critical exponent [J]. Adv Differential Equations, 1996,1 (2): 241-264. [3] Cao D, Yan S. Infinitely many solutions for an elliptic problem involving critical Sobolev growth and Hardy potential [J]. Calc Var Partial Differential Equations,2010, 38: 471-501. [4] Felli V, Terracini S. Elliptic equations with multi-singular inverse-square potentials and critical nonlinearity [J].Comm Partial Differential Equations, 2006, 31 (2): 469-495. [5] Jannelli E. The role played by space dimension in elliptic critical problems[J]. J Differential Equations,1999, 156 (2): 407-426. [6] Abdellaoui B, Felli V, Peral I. Some remarks on systems of elliptic equations doubly critical in the wholeRN[J]. Calc Var Partial Differential Equations, 2009,34 (1): 97-137. [7] Chen Z, Zou W. A remark on doubly critical elliptic systems [J]. Calc Var Partial Differential Equations,2014, 50 (3): 939-965. [8] Chen Z, Zou W. Existence and symmetry of positive ground states for a doubly critical Schroinger system [J]. Trans Amer Math Soc, 2015, 367: 3599-3646. [9] Huang Y, Kang D. On the singular elliptic systems involving multiple critical Sobolev exponents[J]. Nonlinear Anal, 2011,74(2):400-412. [10] Kang D. Elliptic systems involving critical nonlinearities and different Hardy-type terms [J]. J Math Anal Appl,2014, 420 (2): 930-941. [11] Kang D. Systems of elliptic equations involving multiple critical nonlinearities and different Hardy-type terms inRN[J]. J Math Anal Appl, 2014,420 (2): 917-929. [12] Kang D. Systems of quasilinear elliptic equations involving multiple homogeneous nonlinearities [J]. Appl Matt Lett, 2014,37 (11): 1-6. [13] Kang D, Yu J . Systems of critical elliptic equations involving Hardy-type terms and large ranges of parameters [J]. Appl Math Lett, 2015, 46: 77-82. [14] Vazquez J. A strong maximum principle for some quasilinear elliptic equations[J]. Appl Math Optim,1984,12 (1): 191-202. Ground State Solutions of Elliptic Equations Involving Different Hardy-Type Terms and Multiple Critical Sobolev Exponents KangDongsheng,YuJing,ShangguanXiaotian (College of Mathematics and Statistics,South-Central University for Nationalities,Wuhan 430074,China) We study systems of equations involving critical nonlinearities and different Hardy-type terms.By variational methods,the existence of minimizers to Raleigh quotiens and ground state solutions to the systems is proved. elliptic equation; minimizer; critical exponent; ground state solutions; variational method 2015-07-22 康東升(1967-),男,教授,博士,研究方向:偏微分方程,E-mail:dongshengkang@scuec.edu.cn 國家民委科研基金資助項目(12ZNZ004);中南民族大學研究生創新基金資助項目(2015sycxjj127) O175 A 1672-4321(2015)03-0100-05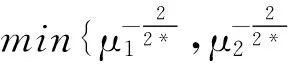
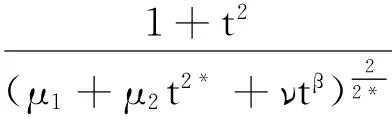
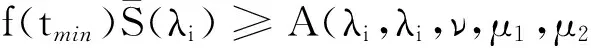

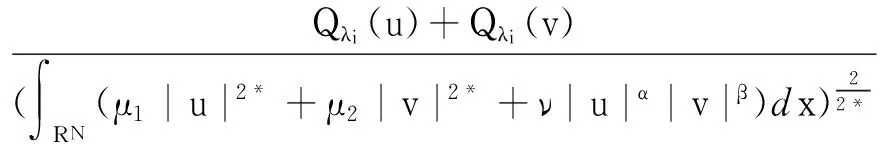
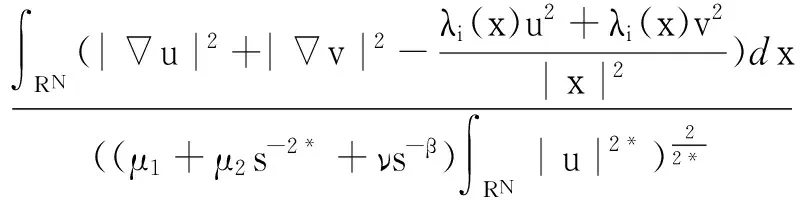
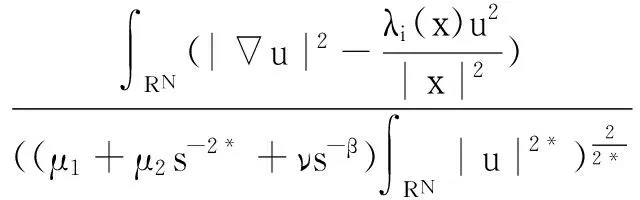
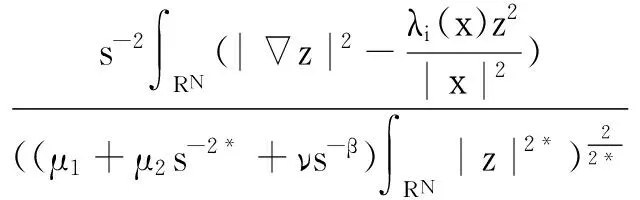
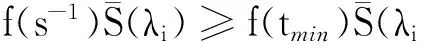
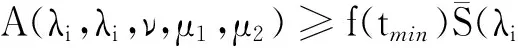
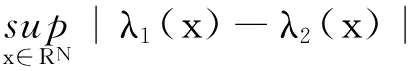
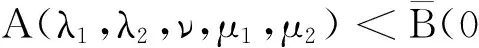
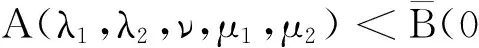
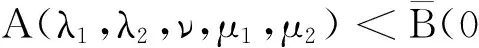

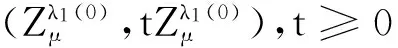
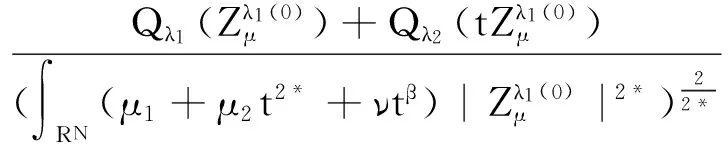
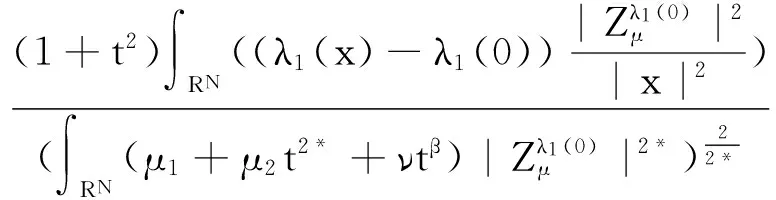
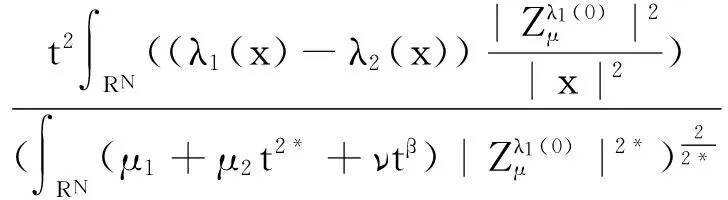
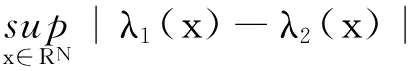
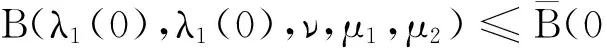
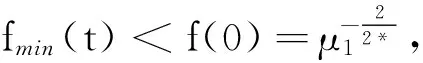
3 基態解的存在