應用于城市軌道交通高架箱梁橋減振降噪的調液阻尼器控制仿真

甘 霖 雷震宇 閆 旭

（1.天津大學科學技術發展研究院，300072，天津；2.同濟大學鐵道與城市軌道交通研究院，201804，上海∥第一作者，碩士研究生）

調液阻尼器（TLD）是一種被動減振裝置，如圖1所示。其工作原理為：受控結構在外荷載激勵下產生振動，激發含液容器中的液體產生晃蕩，一方面由于液體具有慣性，對容器壁產生反方向的動液壓力和波浪力阻礙容器運動；另一方面液體具有黏性，運動過程中會消耗系統一部分能量。當受控結構的運動頻率接近液體的晃蕩頻率時，液體的運動非常激烈，反作用力和能量消耗也最大。

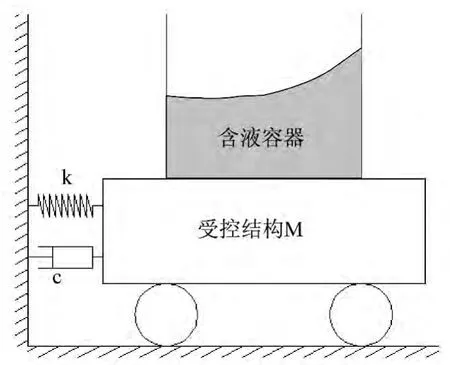
圖1 TLD 作用示意圖

由于TLD 具有構造簡單、安裝方便、造價低廉、可調性好等優點，近年來在土木工程特別是大跨度橋梁、高層建筑和海洋平臺的橫向抗風、抗震和抗冰激振動中得到了廣泛應用［1－3］，但在軌道交通領域的應用并不多見。軌道車輛經過高架橋時，輪軌接觸產生的垂向、橫向輪軌力和荷載偏心力矩經由軌道結構傳遞給橋梁，會引起橋梁的空間彎扭振動，不僅會影響乘客舒適性和橋梁耐久性，振動產生的低頻噪聲輻射還會影響人們的生活。大量研究致力于減小鐵路橋梁的振動和聲輻射，并取得了重要成果［4－6］。有研究者認為箱型梁腹板平面外的橫向振動比平面內隨橋梁的豎向振動對整體噪聲的貢獻更大［7］，因此必須采取措施對腹板的局部振動進行控制。高架箱梁的特殊中空結構作為“天然”的儲液容器，無需架設外部裝置，為TLD 在箱梁橋減振降噪的應用提供了良好條件。本文基于流－固耦合計算理論，利用ANSYS 軟件的有限元方法對箱梁與TLD 的相互作用進行了動力仿真分析，并在Virtual.lab的Acoustics聲學邊界元分析模塊中對安裝前后的箱梁降噪效果進行了對比，對TLD 在軌道交通領域的應用進行了初步探究。

1 理論基礎

1.1 基于ANSYS軟件的流－固耦合有限元法

TLD 中的液體和結構的相互作用是一種復雜的非線性流－固耦合行為。研究者在容器為剛性、液體無黏性等假設下，求得了矩形和圓柱形容器內液體三維晃動的固有頻率解析解［8－9］。但實際上容器的變形和流體動壓力的分布互為因果，流體對結構的影響很大，對工程中具有復雜邊界條件的問題如果同時考慮兩種物理場的交叉耦合作用，很難給出解析表達，可借助有限元軟件進行數值計算。

流－固耦合數值計算的關鍵是合理選取流體坐標系建立控制方程并對控制方程進行離散求解。為方便處理移動邊界或大變形問題，經常采用任意拉格朗日－歐拉法對流體進行描述，并用有限元法離散控制方程。離散后的結構和流體控制方程為：

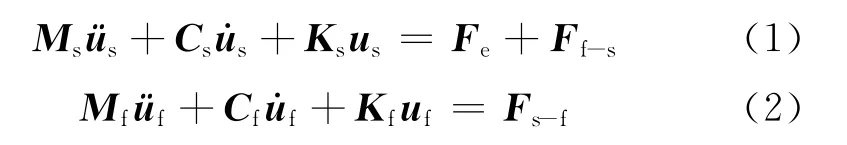
式中：

M——質量矩陣；

K——剛度矩陣；

C——阻尼矩陣；

F——廣義荷載向量；

u——廣義位移向量；

s，f，e——分別表示結構、流體、外荷載。

在ANSYS軟件中，用Shell63 單元和Fluid80分別對薄壁容器和液體進行離散，保持流體和固體網格一致，將與容器側壁和底面接觸的流體單元節點與鄰近容器單元節點進行法向自由度耦合，將自由液面單元添加重力彈簧模擬重力效應，分別將液體自由液面節點豎向位移和容器側面法向位移作為主自由度，利用模態縮減法進行求解即可。

1.2 基于Virtual.lab的噪聲求解邊界元法

利用有限元法求得結構體表面的振動響應之后，要求得空間中某點的輻射聲壓，就是求解波動方程的Neumann邊值問題。如圖2所示。

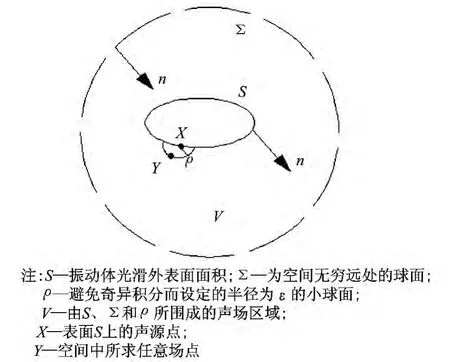
圖2 邊界元法求解示意圖

對波動方程進行傅里葉變換得到單頻簡諧激勵下的Helmholtz波動方程，用加權殘值法求解，可得積分形式的Helmholtz方程式：

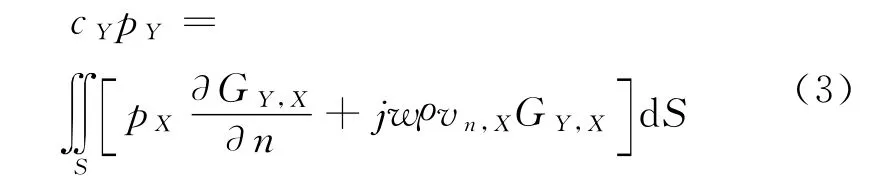
式中：

n——法向量；

j——虛數單位；

w——角頻率；

ρ——流體密度；

2vn，X——X點的法向振動速度。

將振動體表面S進行離散，構造差值函數，得到離散形式的Helmholtz方程；依次將振動體表面的節點作為場點進行循環，可以得到邊界元矩陣方程；利用坐標轉換解決奇異積分，采用CHIEF 方法克服特征頻率處解的非唯一性問題，即可得到振動體表面的聲壓向量。利用式（3）即可求得空間任意場點的聲壓。

在不考慮聲波對結構振動的影響時，結構振動與噪聲輻射的關系為弱耦合。利用有限元軟件和聲學邊界元軟件進行聲振耦合計算的步驟為：①在Virtual.lab的聲學邊界元模塊中導入ANSYS軟件的結果文件（.rst）作為結構網格，提取結構網格的表面網格作為邊界元網格，導入場點網格；②設置結構和流體屬性；③將結構網格上的振動數據映射到邊界元網格上；④定義聲學邊界條件；⑤設置計算參數并進行聲場分布計算；⑥場點聲學響應計算及輸出。

1.3 荷載激勵的數值模擬法

城市軌道交通車輛與鋼軌的相互作用通過軌道結構傳遞給橋梁，引起高架橋梁結構的振動，輪軌力與很多因素有關，具有一定的隨機性，移動常量力模型和移動簡諧力模型都無法表達輪軌力的隨機特性，大量實測數據表明單輪荷載在車輛軸重一半附近上下波動，符合正態分布規律［10］，因此，本文提出用高斯白噪聲模擬單輪載荷譜。假設車輛軸重為P0，采樣點數為N，正態分布標準差為σ，利用Matlab矩陣實驗室標準正態分布隨機序列生成函數的輪軌力

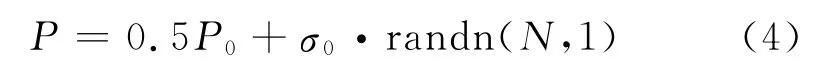
式中：

σ0——正態分布標準差；

randn（N，1）——隨機序列生成函數。

2 計算參數

圖3為列車－橋梁－TLD 動態系統相互作用圖。輪軌力取移動荷載列模型：車體長22 m，定距15.5 m，轉向架軸距2.5 m，P0＝160 kN，σ＝10 kN。為簡化計算，取單節列車，只考慮垂向荷載。作用在鋼軌上的車輪荷載分布和單輪荷載模擬曲線如圖4所示。

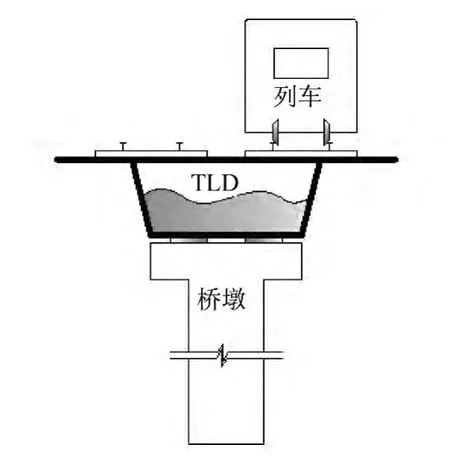
圖3 列車－橋梁－TLD 系統示意圖

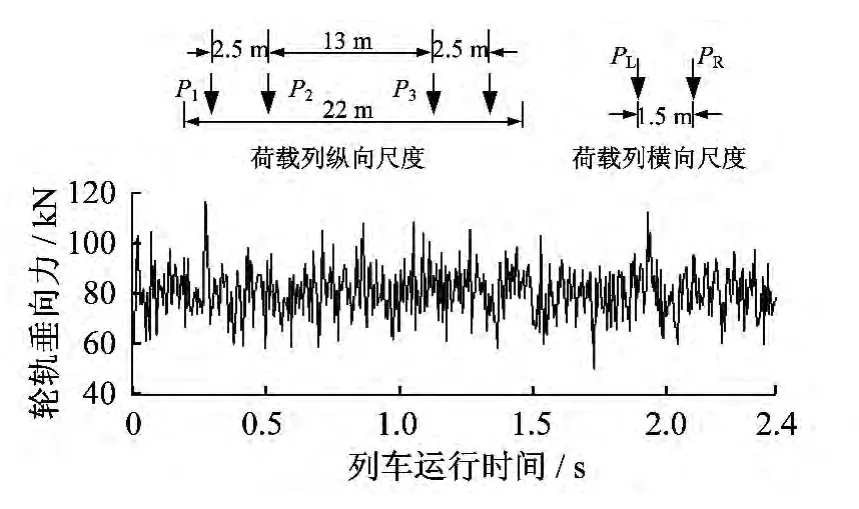
圖4 輪軌力分布及仿真載荷譜

假定地鐵車輛以72 km／h（20 m／s）的速度運行，軌道和橋梁結構參數如表1中所示。當列車前轉向架前輪剛好到達橋頭時開始計時，列車后轉向架后輪剛好駛出橋梁區段時結束計時，期間列車行駛距離為48 m，運行時間為2.4 s，采集樣本數據481個。

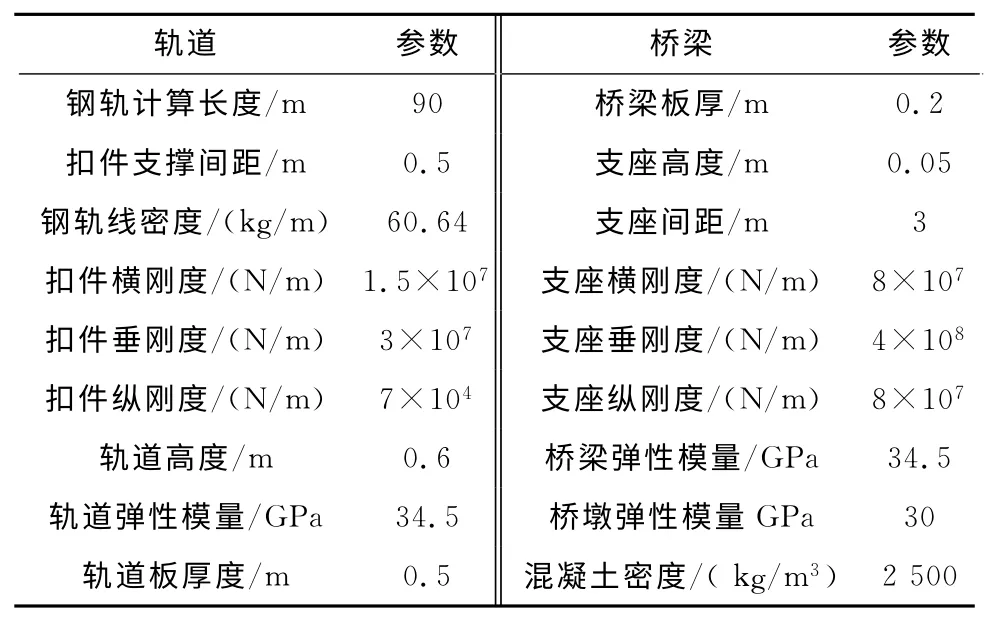
表1 軌道和橋梁結構參數

3 仿真結果

對圖3所示高架箱梁來說，假設預裝TLD 內的液體為水，將水的質量控制在單跨箱梁質量的5%左右，計算需要水的體積為13 m3。將TLD 關于箱梁跨中點所在豎向截面鏡像布置。本文只研究單個TLD 的情形，通過控制TLD 的縱向尺度來控制TLD 的水深，分別對水深0.5 m、1 m 和1.5 m3種工況進行研究。

3.1 橋梁振動特性

由于橋梁支座的彈性和橋墩的柔性，橋梁在運營狀態的頻率與在自然狀態下的頻率有很大差別。利用ANSYS軟件計算了單跨橋梁在考慮支座和橋墩柔性前提下的前6階振動頻率（如圖5中a～f）所示。由圖5可知，橋梁振動的主要振動形式為扭轉振動和豎向彎曲振動。試驗表明，豎向輪軌力在0.5～10.0Hz低頻范圍內占有一定比重，與橋梁主要頻率接近。軌道交通雙線箱梁橋多承受豎向偏心荷載，很容易使橋梁因共振失穩導致支座破壞、梁體裂紋萌生甚至側翻，因此利用TLD 抑制橋梁在10 Hz以內頻段的共振尤為重要。

ANSYS軟件在進行瞬態動力分析時一般通過瑞利阻尼控制整體阻尼。計算公式為：

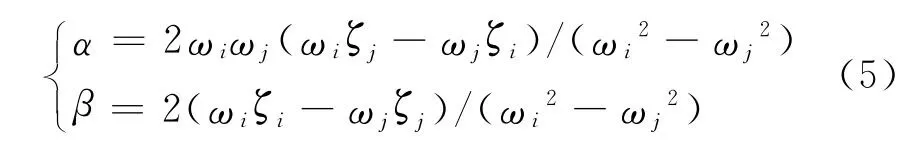
式中：

α，β——瑞利阻尼系數；

ωi，ωj——分別為結構第i和j階固有頻率；

ζi，ζj——分別為結構第i和j階固有頻率對應的阻尼比。

假設結構的前兩階頻率對應的阻尼比ζ1＝ζ2＝0.05，與結構的前兩階固有頻率ω1＝1.998，ω2＝2.600代入式（5），得到瑞利阻尼系數分別為α＝0.113，β＝0.022，在ANSYS軟件中進行瞬態分析，并將計算結果導入Virtual.lab中進行聲輻射計算。

圖5 橋梁前六階模態振型及頻率

3.2 TLD對橋梁豎向振動的影響

為探索TLD 對鐵路橋梁豎向振動特性的影響，取橋梁跨中點所在豎向截面與軌道中心線所在豎向截面的交線在橋面上的投影點為振動參考點，不同工況下箱梁表面振動參考點的垂向位移、速度和加速度時程曲線分別如圖6所示。在不同水深條件下，振動參考點的速度和加速度均方根值如表2中數據所示。

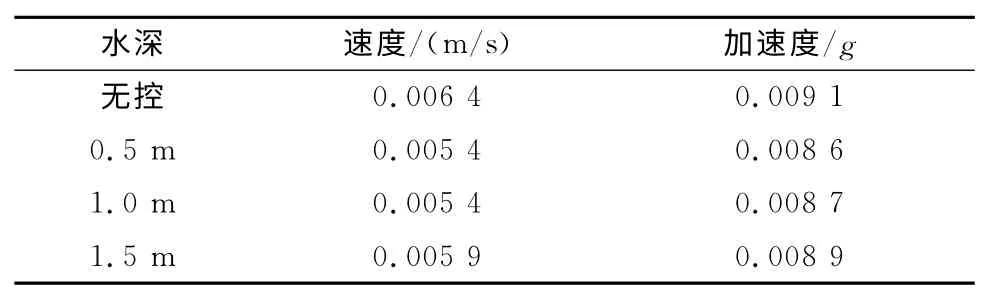
表2 不同水深條件下振動參考點速度和加速度的均方根值（豎向）

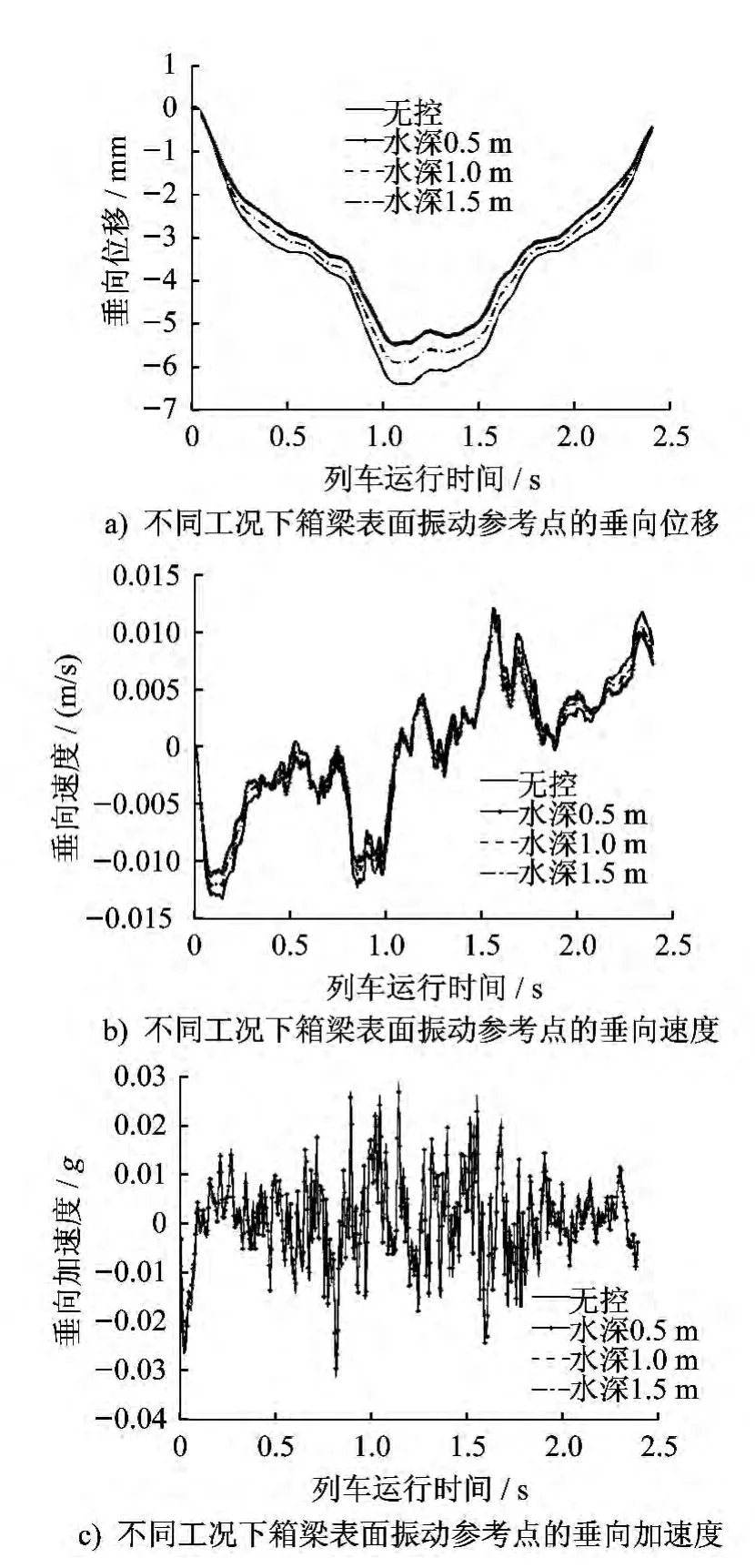
圖6 橋面參考點豎向振動曲線

圖6中顯示，在安裝水深0.5m、1.0m 和1.5m 的TLD后，橋面的垂向位移峰值分別減小14.1%、14.0%和7.8%，速度峰值分別減小13.5%、12.8%和8.3%，加速度峰值分別減小5.3%、4.4%和2.5%。對比發現，TLD對橋面的豎向減振具有一定作用，但減振作用有限，且淺水TLD的減振作用更明顯。

3.3 TLD對橋梁橫向振動的影響

為探索TLD 對鐵路橋梁橫向振動特性的影響，取橋梁一側腹板中心點為振動參考點，不同工況下箱梁表面振動參考點的橫向位移、速度和加速度時程曲線分別如圖7所示。不同水深條件下振動參考點速度和加速度的均方根值如表3所示。

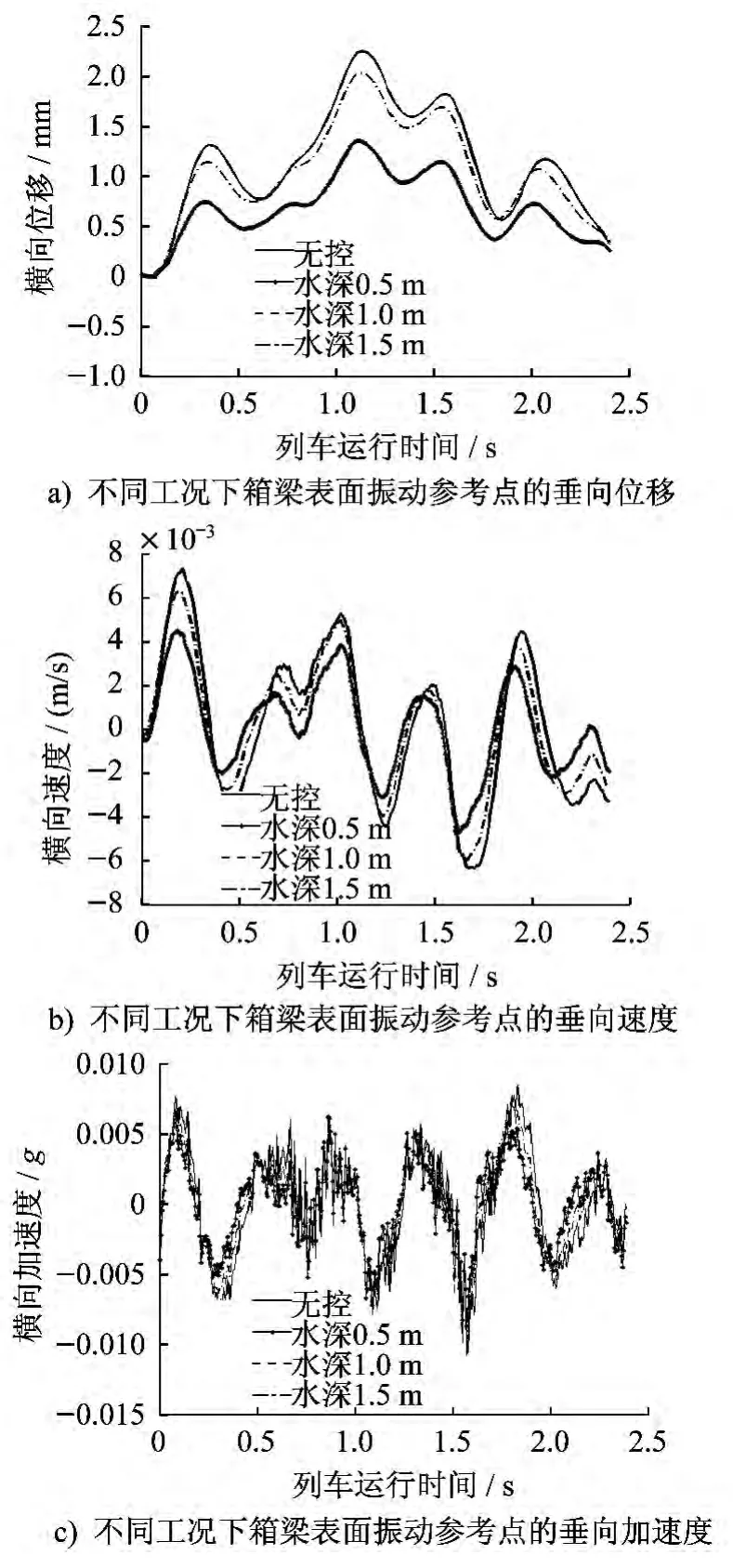
圖7 橋面參考點橫向振動曲線

從圖7中可以看出，安裝TLD 后，不同水深下腹板的橫向振動特性發生根本改變：在水深0.5m、1.0m 和 1.5m 下，位移峰值分別減小40.9%、40.0%和9.1%，速度峰值分別減小35.6%、35.0%和15.1%，加速度峰值分別減小18.8%、18.1%和9.1%。可見，TLD 對橋梁的橫向減振效果很明顯，且不同水深的TLD 都具有可觀的減振效應，淺水TLD 晃動產生的波浪力反作用力對橋梁橫向位移的反作用效果更好。

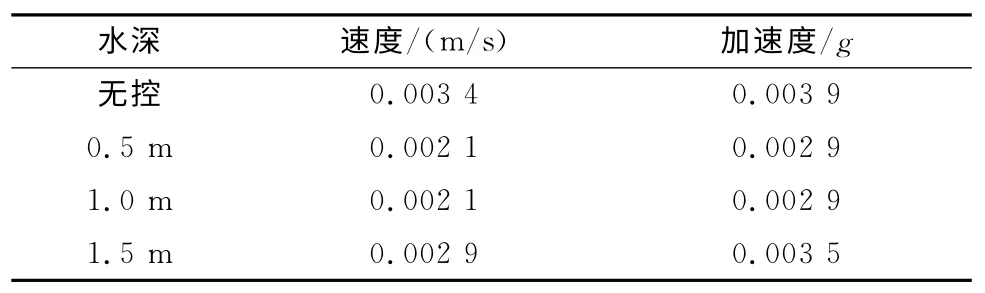
表3 不同水深條件下振動參考點速度和加速度的均方根值（橫向）

3.4 TLD對橋梁噪聲輻射特性的影響

為探索TLD 對空間場點聲壓級的影響，選取與腹板中心點水平距離為10 m 處的空間點為聲壓參考點，該參考點在列車經過橋梁時間段內的未計權時域聲壓級變化如圖8所示。

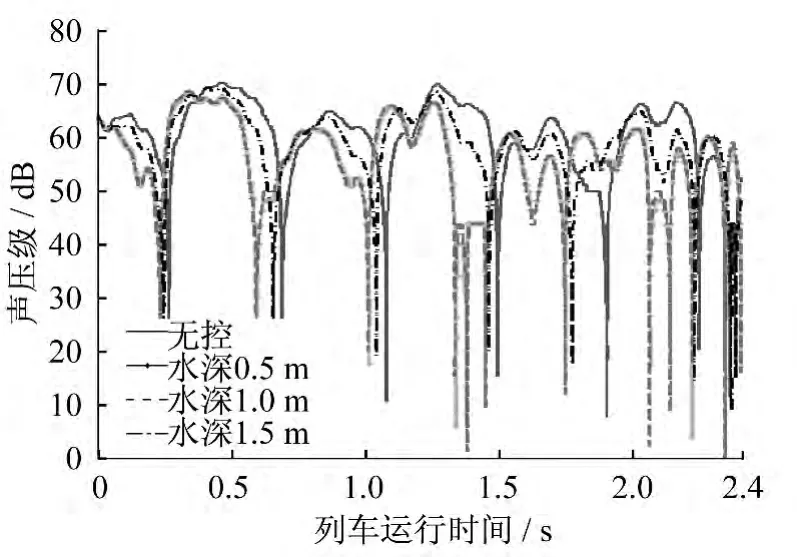
圖8 橋面輻射噪聲時域變化曲線

圖8中顯示，TLD 對橋梁的聲輻射影響很大。無控條件下，列車經過橋梁的過程中，聲壓參考點的最大聲壓級為69.9 dB，平均聲壓級為59.9 dB；安裝TLD 后，在水深分別為0.5 m、1.0 m 和1.5 m下，參考點的最大聲壓級分別為68.3 dB、68.2 dB和68.9 dB，平均聲壓級分別為55.6 dB、55.5 dB和58.3 dB。可見，安裝TLD 可以有效減小橋梁輻射聲壓級最大可達5 dB左右。

為探索TLD 對空間場點聲壓級的影響，選取列車前轉向架前輪剛好到橋梁跨中點，即t＝0.75 s時刻，分別繪制不同工況下橋跨中點所在豎向截面附近場點的聲壓云圖如見圖9。圖中顯示，TLD 對聲壓在空間的分布情況影響不大，但對場點聲壓在該時刻的瞬時值影響很大，且箱梁頂板和底板的較大輻射面積導致板塊附近的聲壓級很大。

4 結語

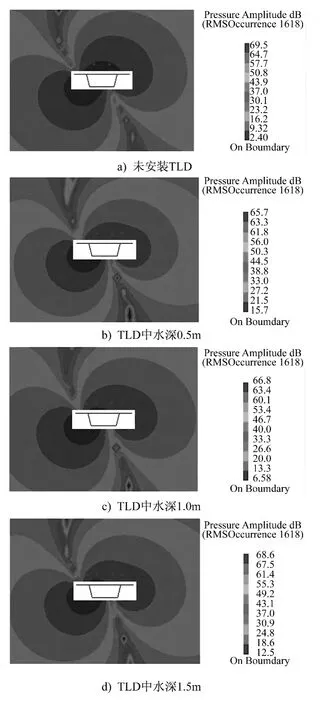
圖9 不同工況下空間場點的聲壓云圖

本文利用ANSYS有限元軟件模擬了安裝TLD前后，高架箱梁橋表面的振動變化情況，并將振動結果導入Virtual.lab中進行了結構噪聲輻射分析，探索了TLD在城市軌道交通領域的適用性，結論如下：

（1）安裝TLD 可以在一定程度上減小軌道中心線處橋面的豎向位移、速度和加速度峰值，但作用并不明顯，建議在實際工程中探索其他措施控制橋梁的豎向振動。

（2）TLD 的橫向減振功能在城市軌道交通高架箱梁橋上可以得到很好的發揮，安裝合適的TLD，可以將橋梁的橫向振動峰值減小20%～40%左右。

（3）安裝TLD 的箱梁橋腹板附近橫向場點的聲壓最大可以降低5 dB左右；安裝前后，空間聲場的分布情況變化不大，輻射面積較大的頂板和底板附近聲壓級相對較大。

［1］王永剛.鐵路斜拉橋車橋動力響應的TLD 控制研究［J］.中國鐵道科學，1999，20（3）：70.

［2］賈影，李宏男，李玉成.高層建筑利用TLD 減震的實例計算［J］.地震工程與工程振動，2000，20（1）：135.

［3］李昕，孫寧，金橋，等.海上平臺利用TLD 的減震研究［J］.船舶力學，2009，13（4）：615.

［4］Mitsuo Kawatani，Chul－Woo Kim，Naoki Kawada，etal.Assessment of traffic－induced low frequency noise radiated from steel box girder bridge［J］.Steel Structures，2008（8）：305.

［5］K.Alten，R.Flesch.Finite element simulation prior to reconstruction of a steel railway bridge to reduce structureborne noise［J］.Engineering Structures，2012（35）：83.

［6］劉寶山，趙國忠.隨機激勵下結構振動聲輻射的靈敏度分析和優化設計［J］.振動工程學，2011，24（3）：309.

［7］韓江龍，吳定俊，李奇.城市軌道交通高架結構噪聲研究進展［J］.城市軌道交通研究，2012（3）：109.

［8］林江，朱召泉.船閘閘門受撞安全性研究［J］.水運工程，2007（6）：78.

［9］賈善坡，許成祥.儲液容器內液體自由晃動的有限元分析［J］.船舶力學，2012，16（1－2）：21.

［10］王建西，許玉德，練松良.隨機輪軌力作用下鋼軌滾動接觸疲勞裂紋萌生壽命預測仿真［J］.鐵道學報，2010，32（3）：67.