土方調配優化中的問題及其解決方法
任旭凱 寧曉冬 段景艷
(河南化工職業學院,河南 鄭州 450042)
土方調配優化中的問題及其解決方法
任旭凱 寧曉冬 段景艷
(河南化工職業學院,河南 鄭州 450042)
在土方調配中,對土方調配的求解方法通常采用線性規劃法中的“表上作業法”進行改進,采用“表上兩側夾逼作業法”。這種方法可以提高工作效率,減少檢驗等步驟,可一次性得到更為準確、高效的最優解。
土方調配;兩側夾逼
1.現狀
土方調配的實質是已知各挖土區和各填土區的位置以及各挖土區和各填土區之間的運距,求各挖土區向各填土區調配的土方量,滿足總的運輸費用最低。
目前土方調配的求解方法常用線性規劃中的“表上作業法”[1][2][3]。這種方法的缺點是:工作量大,效率低,準確率不高,需要檢驗和調整,并且在多次調整之后還有可能不能滿足要求。
2.調配優化
由于已有“表上作業法”存在各種不足,現采用“表上兩側夾逼作業法”對其進行優化處理。
2.1 建立模型
土方平衡與運距表

表1
根據約束條件知道:任意一個挖方區Ai(填方區Bj)對應n(m)個填方區(挖方區),其中運距與總運費正相關,既應盡量選擇運距小的,避免使用運距大的,這樣才可以有效降低總運費。但每一個挖方區Ai與其他m-1個挖方區和n個填方區之間又有間接聯系。然而,一個挖方區對應的各填方區中最大運距和最小運距的差,如果大于另一挖方區對應的各挖方區中最大運距和最小運距的差,則第一個挖方區對填土區的選擇相對于第二個挖方區來說,將對總運費影響更大,同理可適用于次最大運距和次最小運距等。
因此,我們在選擇土方調配時,首先給各個挖方區對應的最大運距和最小運距的差中最大的賦值,再將這個挖方區對應的最大運距和最小運距刪去之后,再次在給各個挖方區對應的最大運距和最小運距的差中最大的賦值,再將這個挖方區對應的最大運距和最小運距刪去。如此反復,直到所有挖方區和填方區全部賦值。如此得到的一組解便是最優解。
2.2 優化實例
下面以具體實例(圖 1,整理為表2)介紹求解步驟(此示例采用表上作業法計算的最優土方運輸量為85000m3·m):

圖1 土方調配示意圖

圖2 土方優化后調配圖
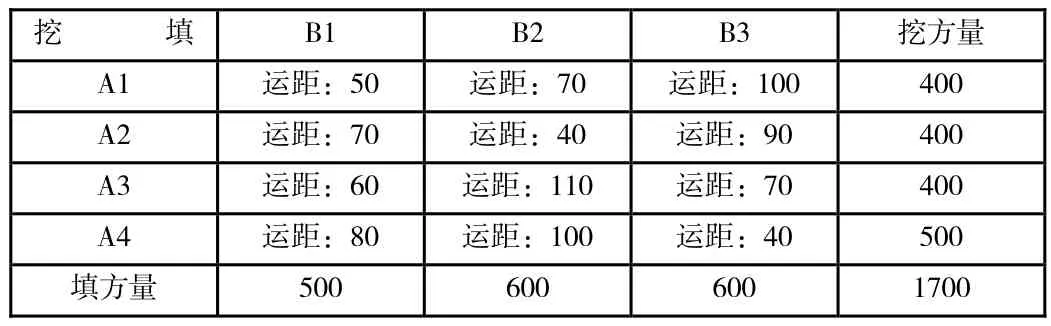
表2
3 結論
以上結果與“表上作業法”經過多次調整后的計算結果相同,但計算結果可以一次性得到,不需要重復檢驗和調整,有效的提高了工作效率,由此可見,在土方調配施工方案的制作過程中,使用“表上夾逼作業法”是一種更為準確、高效的作業方法。
[1]張國聯,王鳳池主編.土木工程施工[M].中國建筑工業出版社.2006
[2]趙志縉,應惠清主編.建筑施工[M].同濟大學出版社.2009
[3]張立新主編.土木工程施工組織設計[M].中國電力出版社.2007
Earthwork allocation optimization problems and its solution
REN Xu-kai, NING Xiao-dong, Duan Jing-yan
(Henan Vocational College of Chemical Technology,Henan 450042,China)
In the earthwork allocation, the deployment of Turkish solving method commonly used in the current planning act the "tabular method" is improved into a "folder on both sides of the table to force the working method". This method can improve efficiency, reduce testing and other steps, and can be a more accurate and efficient optimal solution.
earthwork allocation; force on both sides of the clip
G322
B
1007–6344(2015)01–0329–01
任旭凱(1987-),男,河南陜縣人,碩士,研究方向:地下結構計算理論。

