地下工程相似模型試驗與實際工況的對比分析及誤差研究

趙吉昌 梁 意 張 裕 何 韻

(1.后勤工程學院軍事建筑工程系，重慶 401311 ； 2.61769部隊，山西 032100) (3.后勤工程學院國防建筑規劃與環境工程系，重慶 401311)

地下工程相似模型試驗與實際工況的對比分析及誤差研究

趙吉昌1梁 意2張 裕1何 韻3

(1.后勤工程學院軍事建筑工程系，重慶 401311 ； 2.61769部隊，山西 032100) (3.后勤工程學院國防建筑規劃與環境工程系，重慶 401311)

作為當前研究地下工程整體穩定性方面的主流方法，相似物理模型試驗通過控制邊界條件和材料特性，制作與實際地質環境相似的物理模型，應用現代化的試驗加載方式和監測手段進行有目的、多角度研究，從而降低了試驗規模，節約了試驗成本并縮短了試驗周期。然而，相似物理模型能否真實地表征實際工程環境并如何合理選取控制量是當前急需解決的問題。本文以公路雙車道為例，提出了一種地下工程相似物理模型試驗與數值計算結果特征參數的誤差分析方法，分別考慮了其在開挖和應力釋放后增加了襯砌支護的特征點變形參數，并與不同相似常數下的相似模型特征點參數作對比分析，得到的結論是：一是相似物理模型試驗無法保證隧道開挖過程中的特征點參數物理相似，因而是不適合做開挖過程的變形和破壞機理方面的測試研究；二是相似物理模型試驗在襯砌支護后特征點參數能夠保證物理相似，但仍有不同程度的誤差，在相似常數為20時的誤差相對較小且經濟合理。

相似模型試驗；對比分析；數值模擬；公路雙車道；相似常數

1 引言

地下工程是指修建在地表以下地層中的工程結構物，即在地下開挖的各種隧道、洞室等工程設施。近年來，隨著科學技術的迅猛發展和人類文明的進步，地下空間的作為一種新型資源被充分利用，如今已廣泛應用于礦山、交通、水利水電、通訊、能源儲備以及國防等諸多工程領域。通常認為地下工程具有良好的抗震性能，長期以來未受重視，然而在1995年日本阪神發生了大地震，地鐵車站、隧道等地下工程遭受嚴重破壞[1-5]，打破了多年來地下工程設計偏于安全的神話，自此之后，逐漸引起了專家和學者們的重視，并根據各個國家和地區的地質環境和地震制定了相應的抗震規范[6-9]。

理論上講，在解決現實工程問題時最具有工程意義和說服力的是原場試驗，但由于試驗地質環境復雜、工程量大、投入經費多、可復制性差等原因無法得到普遍應用，只能尋求近似等效的方法來解決。目前各國的抗震規范解決地下工程穩定性的方法主要有理論分析法、數值分析法和模型試驗法三種。其中理論分析法側重于在較多假設條件下結構簡單的連續體模型，利用力學理論、波動理論等知識來推導出理想化的解析解，在解決結構復雜的非線性工況時就顯得無能為力，也只能從近似或定性方面推斷；數值分析法是基于有限元、無限元、有限差分、邊界元、離散元等計算機方法求得工程計算模型近似解的方法，常用數值分析軟件如Flac3D、Ansys、Ls-Dyna等來實現，這些軟件也是基于連續介質力學，在處理巖石、混凝土類材料時本身存在一定的局限性，但由于建模方面，費用低，計算量大且迅速等優點，結合動力時程分析方法和反應譜分析方法也在工程上得到了廣泛應用；模型試驗方法是控制邊界條件和材料特性，通過制作與實際相似的物理模型來模擬原場地質環境（簡稱為原型）和力學狀態，應用現代化的試驗加載和監測手段進行有目的、多角度研究，同時此方法比現場試驗規模小、試驗周期短的優勢，現已成為地下工程結構損傷、破壞和抗震防護的主流方法。

實際上，地下工程問題大多處在半無限空間里，地質環境復雜，力學狀態很難確定，單從一種方法分析是很難合理解釋清楚的，通常是三種或兩種方法結合來對比分析，如文獻[10]將埋入式抗滑樁振動臺模型試驗與數值計算作了對比研究。然而，三種方法都是通過近似等效模型來簡化現實工程環境和力學狀態，顯然會出現方法誤差、隨機誤差、系統誤差、測量誤差等不可避免的問題。本文就以相似物理模型試驗這一方法為例，考慮其能否真實地表征實際工程環境并如何合理選取控制量進行了探討，從而為今后的學者在誤差分析和模型試驗結果預測方法提供依據。

2 試驗部分

2.1 相似理論及基本假設

相似理論是闡述自然界中各相似現象相似原理和規律的學說，它在工程界中主要應用于指導是模型試驗，通常三個相似準則組成。在制作和設計本文所相似物理模型時，只有滿足相似準則并保證與原型相似，才能通過模型試驗結果推算或折算出原型的相應結果。本文就以雙車道公路隧道為例，在滿足單值邊界條件的前提下建立相似物理模型試驗來進行研究。

考慮到公路隧道在自重應力或外荷載作用下的穩定性問題是眾多學者比較關注的，故本文采用重力相似律來對模型進行制作和設計。重力相似律雖然放棄了彈性恢復力的要求，但在觀測隧道的破壞機理和在極限平衡狀態下（臨近破壞階段）的規律是最有代表性的[11]。同時，本文沒有考慮相似物理模型在動力荷載作用下的響應分析，僅考慮隧道在開挖和應力釋放后增加了襯砌支護的穩定性，這可將對所需的控制量參數做以簡化，如式1所示：

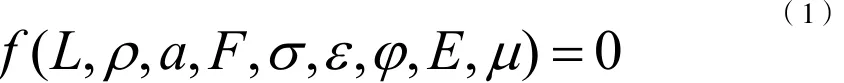
這些量依次分別表示：長度、密度、加速度、力、應力、應變、摩擦角、彈性模量、泊松比。其中前三項為基本控制量，為便于制配相似材料和計算，進一步做如式2和式3的設定：

其他參數均可由這三個基本控制量和無因次的量綱參數推導出來，具體如式（4）－（9）所示：

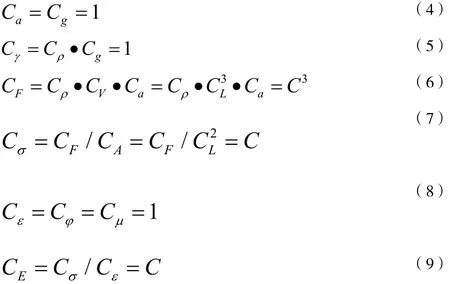
在研究地下工程穩定性問題時還應考慮抗剪強度和粘聚力的影響，根據莫爾－庫侖定理如式（10）所示，

抗剪強度和粘聚力是無法達到絕對相似的，只能通過其他控制量來保證，這也是目前很難做到模型與實際工程地質全面相似的重要原因。

2.2 模型單值性條件設定

任何試驗都難免會出現一些誤差，特別處理一些非線性工程問題時，人們只能用曲線擬合或一些修正參數來預測試驗結果，本文提出的雙車隧道穩定性問題就是一個典型的例子。鑒于絕對大多數試驗是無法進行足尺的原型試驗，且很難在較短的時間內嚴格按照相似關系制作出不同相似參數下的相似物理模型，本文通過FlAC3d這一應用數值軟件來進行數值模擬。將在原型尺寸（即相似常數為1）的特征值參量數值為最可信賴的數值（或稱真值），將相似常數為 10、20、30、40和50的數值為間接得到的值，通過誤差傳遞公式和標準差分析來確定，同時增加雙車隧道的上覆埋深來判斷不同相似常數的模型變形狀態。

雙車隧道的計算模型是按照“自重應力計算－開挖－加初襯”順序進行設計的，且原型和相似物理模型的網格及尺寸完全按照相似理論設計，如圖1所示的是相似常數C為10時的計算模型：

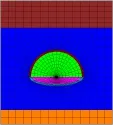
圖1 雙車隧道計算模型

具體的幾何參數和邊界條件如表1所示：

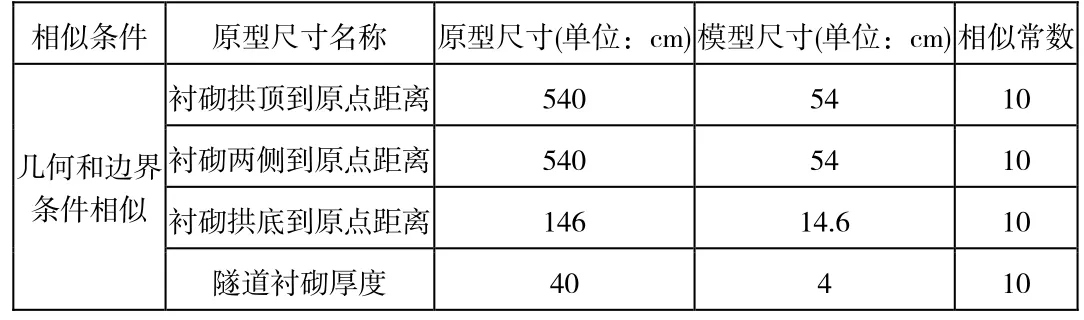
表1 相似模型尺寸及相似常數要求

同時，模型中各材料物理力學參數如表2所示：

表2 模型材料物理力學參數

模型的監測點布置在隧道的拱頂－〉拱底的位置等角度（9°）布置的，在開挖過程中，監測點在毛洞的洞壁上，而增加了初襯后監測點坐標則相應的向隧道中心點減小襯砌厚度的數值，即此時監測襯砌內壁的變形狀態。

3 試驗結果分析及結論

本文分別考慮了地下雙車隧道在開挖和應力釋放后增加了襯砌支護的特征點變形參數，與不同相似常數、不同上覆埋深下的相似模型特征點參數作對比分析。由于位移的變化具有累積效果，而應變和應力狀態則是瞬時的且易實現物理相似，本文就以監測點的位移曲線來對試驗整個過程的變形狀態進行判別。在開挖階段拱頂的位移曲線如圖2所示：

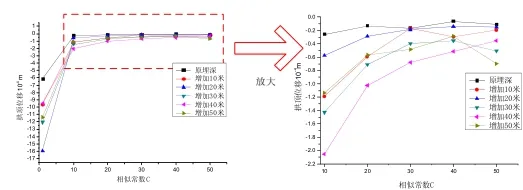
圖2 開挖階段拱頂的位移曲線圖

從圖2不難看出，雖然模型能夠保證幾何相似，但無法保證物理相似，故相似物理模型是不應做開挖階段的模擬與預測的。開挖后隧道因自重應力作用會出現應力釋放現象，同時應力會重新分布，這時增加初襯支護就是為了防止隧道發生失穩破壞，此時隧道內壁拱頂監測點的位移曲線如圖3所示：

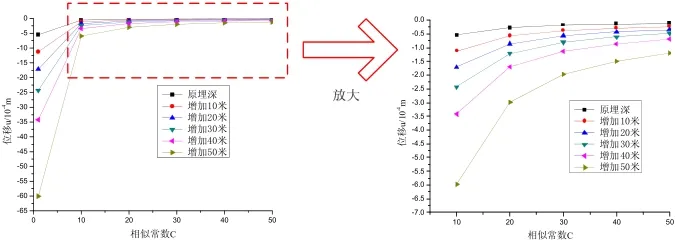
圖3 增加初襯后拱頂的位移曲線圖

顯然，如果在沒有出現大的位移或發生失穩破壞等情況下，應力、應變等變形狀態是可以保證與原型相似的，此時雙車隧道的物理模型試驗能否近似真實地表征原型情況，還應進行誤差分析。拱頂的位移絕對誤差曲線和相對誤差曲線分別如圖4和圖5所示：

圖4 拱頂位移的絕對誤差曲線圖

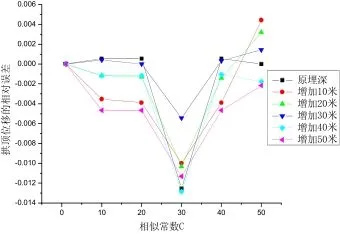
圖5 拱頂位移的相對誤差曲線圖

從誤差曲線圖可以看出，足尺（即原型）的模型試驗誤差最小，隨著相似常數的增加（模型尺寸變小），絕對誤差呈上升趨勢，相對誤差在相似常數為 30時達到峰值。綜合表明，在相似常數為10和20時，相對誤差和絕對誤差較小，比較適合在這個相似常數下進行相似物理模型試驗。同時考慮到試驗場地要求和所需材料、人工等費用，建議雙車隧道的相似物理模型試驗采用相似常數為 20最能表征實際工況。

4結論及展望

本文以公路雙車道為例，提出了一種地下工程相似物理模型試驗與數值計算結果特征參數的誤差分析方法，分別考慮了其在開挖和應力釋放后增加了襯砌支護的特征點變形參數，并與不同相似常數和不同上覆埋深下的相似模型特征點參數作對比分析，得到的結論：

（1）相似物理模型試驗是實現模型與原型的全面相似，但可根據試驗的目的而放棄一些參數的對應關系。如彈性恢復力、抗剪強度和粘聚力等；

（2）地下雙車隧道的相似物理模型試驗無法保證隧道開挖過程中的特征點參數物理相似，因而是不適合做開挖過程的變形和破壞機理方面的監測和預測；

（3）雙車隧道相似物理模型試驗在襯砌支護后特征點參數能夠保證物理相似，但仍有不同程度的誤差。監測點的絕對誤差會隨著相似常數成正比，而相對誤差會有波動，因試驗場地要求和所需材料、人工等費用限制，本文建議在相似常數為20時比較適合雙車隧道的相似物理模型試驗。

[1]Asakura T, Sato Y.Mountain Tunnels Damage in the 1995 HYOGOKEN-NANBU earthquake[J].Railway Technical Research Institute(RTRI),1998,39(1):9-16

[2]Hashash Y M A,HookJ,SchmidtB,et al. Seismic design and analysis of underground structures[J].Tunneling and Underground Space Technology, 2001,(16):247-293

[3]Nakamura S,YoshidaN,IwatateT.Damage to Daikai Subway Station During the1995 Hyogoken-Nambu Earthquake and Its Investigation[J].Japan Society of Civil Engineers, Committee of Earthquake Engineering,1996,287-295.

[4]TajimiM.Damage done by the great earthquake disaster of the Hanshin-A waji district to the Kobe Municipal Subway System and restoration works of the damage [J].JpnRailw Eng1996,137:19-23.

[5]SenzaiSamata,HajimeOhuchi,Takashi Matsuda. A study of the damage of subway structures during the 1995 Hanshin-Awaji earthquake[J].Cement and Concrete Composites,1997,19(3):223-239.

[6]伊藤隆吉.中日橋梁抗震設計規范的比較研究[D].上海：同濟大學，2001

[7]American Association of State Highway and Transportation Officials. AASHTO Guide Specifications for LRFD Seismic Bridge Design,2009

[8]范立礎等.高架橋梁抗震設計.北京：人民交通出版社

[9]范力,趙斌,呂西林.歐洲規范 8與中國抗震設計規范關于抗震設防目標和地震作用的比較[J].結構工程師,2006,22(6):59-63

[10]許江波,鄭穎人.埋入式抗滑樁振動臺模型試驗分析[J].巖土工程學報,2012,34(10):1896-1902

[11]林皋,朱彤,林蓓.結構動力模型試驗的相似技巧[J].大連理工大學學報,2000,40(1):1-8

G322

B

1007–6344（2015）01–0330–02

趙吉昌(1985–)，男，2010年碩士畢業于軍械工程學院，現為博士研究生，主要從事巖土本構關系與軍事地下工程穩定性。