基于曲面擬合模型的山區GNSS水準精度分析

房新玉，陸偉，姚曉偉

（交通運輸部天津水運工程科學研究所水運工程測繪技術研究中心，天津300456）

基于曲面擬合模型的山區GNSS水準精度分析

房新玉，陸偉，姚曉偉

（交通運輸部天津水運工程科學研究所水運工程測繪技術研究中心，天津300456）

介紹了測量中的高程系統及其轉換關系，對GNSS水準模型進行了簡要介紹。通過實例對山區GNSS水準曲面擬合的精度進行了分析，并對GNSS水準精度和外圍點的精度進行了評定，得到了一些有工程價值的結論。

GNSS；高程擬合；正常高；大地高；擬合精度

GNSS水準高程擬合研究是為了實現由GNSS大地高求出水準高，用GNSS水準代替幾何水準，提高GNSS水準測量的精度，發揮GNSS技術提供三維坐標的優越性［1-2］。

采用GNSS測定正高或正常高，成為GNSS水準。通過GNSS測出的是大地高，要確定點的正高或正常高，需要進行高程系統轉換，即確定大地水準面差距或高程異常［1-3］。

大地高程系統是以參考橢球面為基準面的高程系統，它是一個幾何量，不具有物理意義。GNSS定位測量獲得的是WGS-84坐標系下高精度的大地高，大地高一般用H表示［4-5］。

正高是以大地水準面為基準面的高程系統，它是唯一確定的數值，可以用來表示地面點的高程，但由于地殼質量分布的不均勻，正高不可能準確求定，正高用Hg表示。

圖1 大地高、正高、正常高關系圖Fig.1 Relationship of geodetic height，orthogonal height and normal height

正常高是以似大地水準面為基準的高程系統，正常高用Hr表示［4-5］。

似大地水準面到參考橢球面的距離成為高程異常，用ξ表示。大地高和正常高的關系可以表示為

如果高程異常已知，通過式（1）就能進行大地高和正常高之間的相互轉換，但當其未知時，則需要設法確定高程異常的數值。確定高程異常的基本方法有天文大地法、大地水準面模型法、重力測量法和幾何內插法及殘差模型等方法。下面以幾何內插法為例，介紹高程擬合的方法［4-5］。并利用曲面擬合模型對GNSS水準在山區的擬合精度進行分析。

1 幾何內插法的數學模型

幾何內插法的基本原理就是通過一些既進行了GNSS觀測，又進行了水準測量的公共點獲得相應的高程異常，采用平面或曲面擬合、配置、三次樣條等內插方法，擬合出測區的高程異常面，進而求出待求點的正常高［1-2］。

在進行多項式內插時，可采用不同階次的多項式。假定（x,y）為測區內任一點的高程異常，其高程異常值為ξ

f(x,y)為測區內高程異常擬合的數學模型。則可將高程異常表示為下面的多項式形式零次多項式（常數擬合）

一次多項式（平面擬合）

二次多項式（曲面擬合）

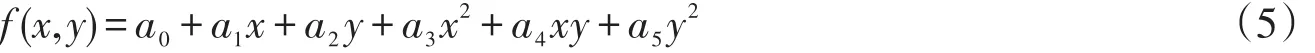
若采用零次多項式進行內插，至少需要1個公共點；若采用一次多項式進行內插，至少需要3個公共點；若采用二次多項式進行內插，至少需要6個公共點。然后利用最小二乘原理解算出多項式系數，從而確定測區的高程異常曲面，利用擬合出的曲面，內插出其他GNSS點的高程異常，從而求出各個待求點的正常高。

零次多項式適用于高程異常變化平緩的地區，如果GNSS和水準聯測點較高的情況，在控制點周圍4 km范圍內，可以達到3 cm的精度［6］。

一次多項式適用于高程異常變化平緩的地區且控制點較少的情況，它的精度情況與GNSS水準聯測點的分布和精度情況有關，它的擬合精度要高于零次多項式的擬合精度而低于二次多項式擬合的精度［7］。

二次多項式適用于控制點較多的情況，可以應用于流域、平原和山區，它的精度情況與GNSS水準聯測點的分布和精度情況有關，精度要優于一次多項式擬合的精度［6-7］。

2 實例分析及擬合精度

2.1 實例分析

測區位于南方某沿海地區，3條河流自西向東貫穿該地區，3條河流之間為山區，測區東西向長約65 km，南北向長約78 km，測區范圍為3 400 km2，共有水準聯測點39個，其水準為二等，部分為三等，分布情況如圖2所示。

2.2 觀測值權陣確定

高程異常的精度受GNSS和準測量精度的雙重影響，根據公式（1）可知

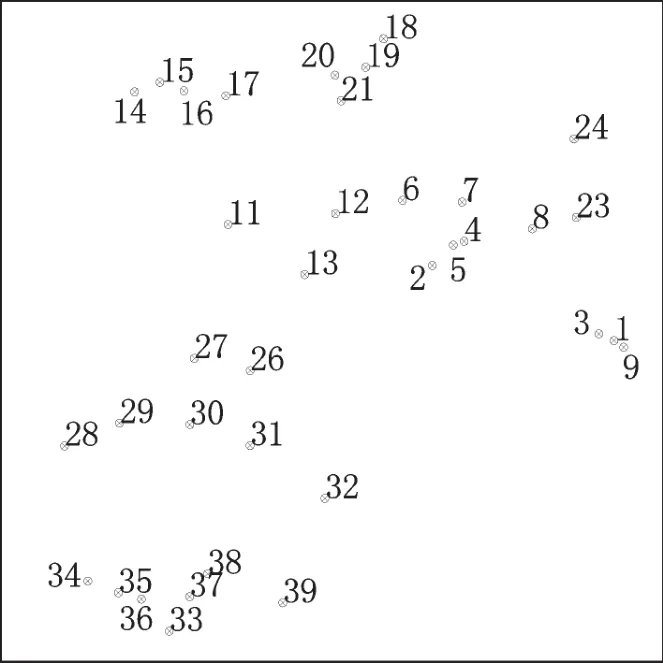
圖2 水準聯測點點位分布圖Fig.2 Distribution of benchmark

GNSS靜態大地高的精度與二等水準測量的精度相同［8］，根據水準測量規范規定的各個等級水準的限差要求，設定GNSS大地高和水準的權重如表1，并依此推定高程異常的權。

2.3 擬合精度分析

在對數據粗差點10，22，25進行剔除后，按以下5種方案采用曲面擬合法對測區擬合情況進行分析。

表1GNSS大地高和水準的權Tab.1 Weight of GNSS geodetic height and benchmark

（1）點位均勻分布于整個測區，選擇控制點5，9，12，14，18，24，26，34，39共9個點作為擬合點，其余點作為校核點；（2）點位均勻分布于測區中部，選擇控制點2，7，11，21，26，30，32，38共8個點作為擬合點，其余點作為校核點；（3）點位均已分布于測區北部，選擇控制點2，6，9，11，14，18，21，24共8個點作為擬合點，其余點作為校核點；（4）點位均勻分布于整個測區，選擇控制點3，5，13，15，19，31，35，38共8個點作為校核點，其余點作為擬合點；（5）采用分區擬合，分北部、中部、南部三區分別進行擬合，區與區之間有公共點。控制點11、13作為北部和中區部擬合的分界點和公共點，控制點28、32作為中部和南部區域的分界點和公共點。分區擬合時，分別在北部選擇4、12、16校核點，中部選擇27、29作為校核點，南部選擇35、38作為校核點。

從表2中可以看出：

（1）擬合點的高程異常之差小于校核點，顯然，這是因為擬合模型是依靠擬合點高程異常數據建立起來的；（2）方案1的內符合精度、外符合精度均較大，大于5 cm，這是由于擬合點較少，且擬合的面積較大造成的；（3）方案4的內符合精度大于5 cm、外符合精度均較小，這是由于擬合區域較大，造成內符合精度較大；參與擬合的點較多，因此外符合精度較小；（4）方案2、方案3和方案5的內符合精度、控制點覆蓋范圍內的外符合精度均較小；這是由于擬合的區域較小；（5）方案2和方案3控制點覆蓋范圍外的外符合精度比較大，因此，控制點覆蓋范圍外的不能應用該擬合結果。

2.4GNSS水準精度評定

內符合精度和外符合精度是絕對精度評定的方法，相對精度的評定為根據檢核點至已知點的距離L（km），按幾何水準限差計算檢核點擬合殘差的限值（表2），將殘差與限值比較，評定GNSS水準的精度。

以方案3為例，對控制點覆蓋范圍內的GNSS水準精度進行評定，該表中：平均值內符合精度；外符合精度

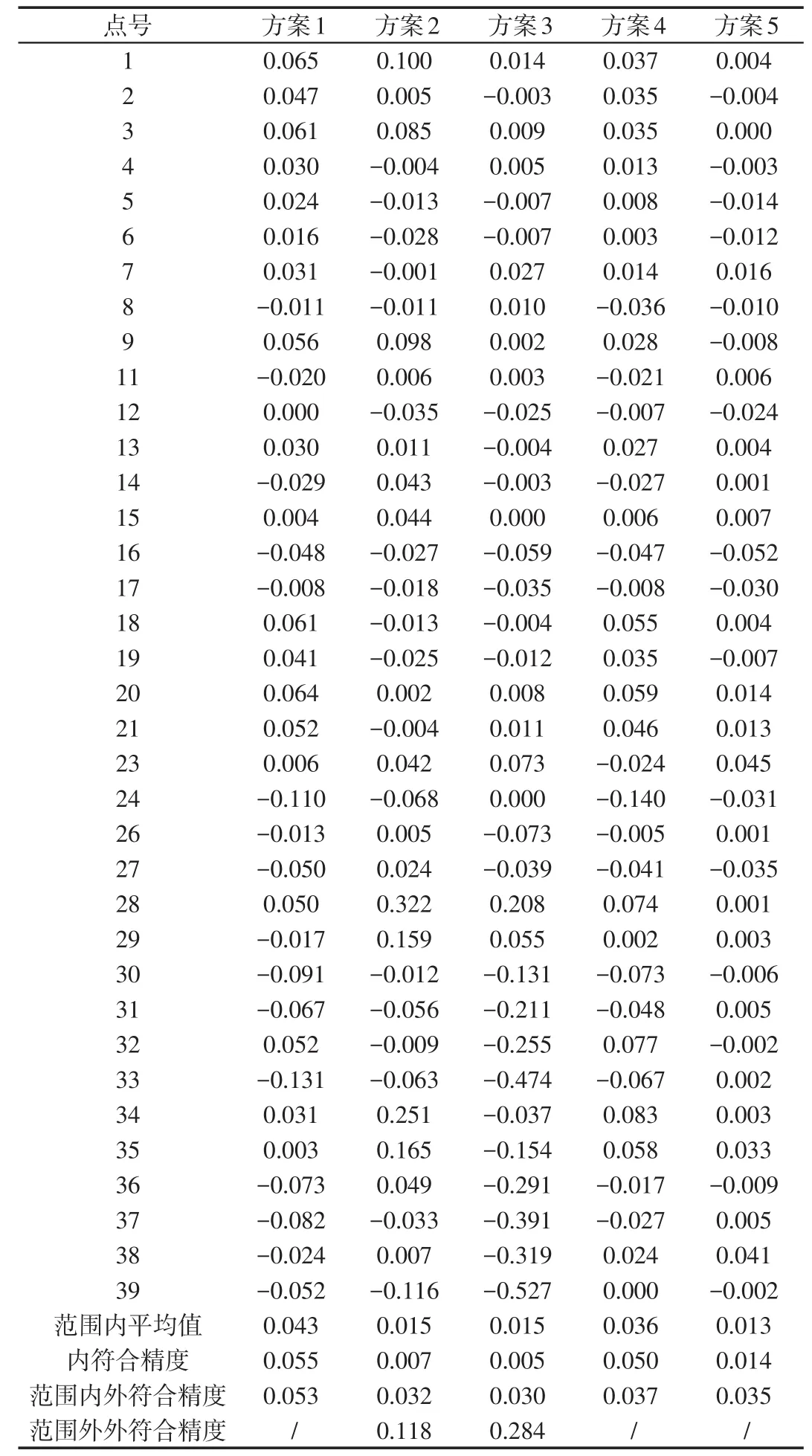
表2 不同方案高程異常擬合結果與幾何水準計算異常結果之差值Tab.2 Difference of height anomaly fitting results using different schemes and geometric leveling m

表3GNSS水準限差［11］Tab.3 Tolerance of GNSS benchmark

圖3GNSS水準精度評定點位分布圖

Fig.3 Distribution of GNSS benchmark accuracy evaluation區域東西長約60 km，南北寬約38 km，面積約1 325 km2，控制點分布情況如圖3所示。

根據方案3和表3，得到了GNSS水準精度評定情況，如表4所示。

除了16、23號控制點高程異常差值在四等限差和等外限差之間，其他點均滿足三等水準測量精度需求；16號點距最近14號點的實地距離約為9.2 km，此時的四等限差為0.061 m，滿足四等規范要求；23號點距最近的24號點實地距離約為14 km，此時的四等限差為0.075 m，擬合精度滿足四等規范要求。從圖3中可以看出，23號點位于測區邊緣，且距測區最近參與擬合控制距離較遠，因此，在測區邊緣，參與擬合的控制點間距盡可能的不要太大。

從以上分析GNSS水準的擬合精度滿足四等水準測量精度的要求，大部分情況可以滿足三等水準測量精度的要求。

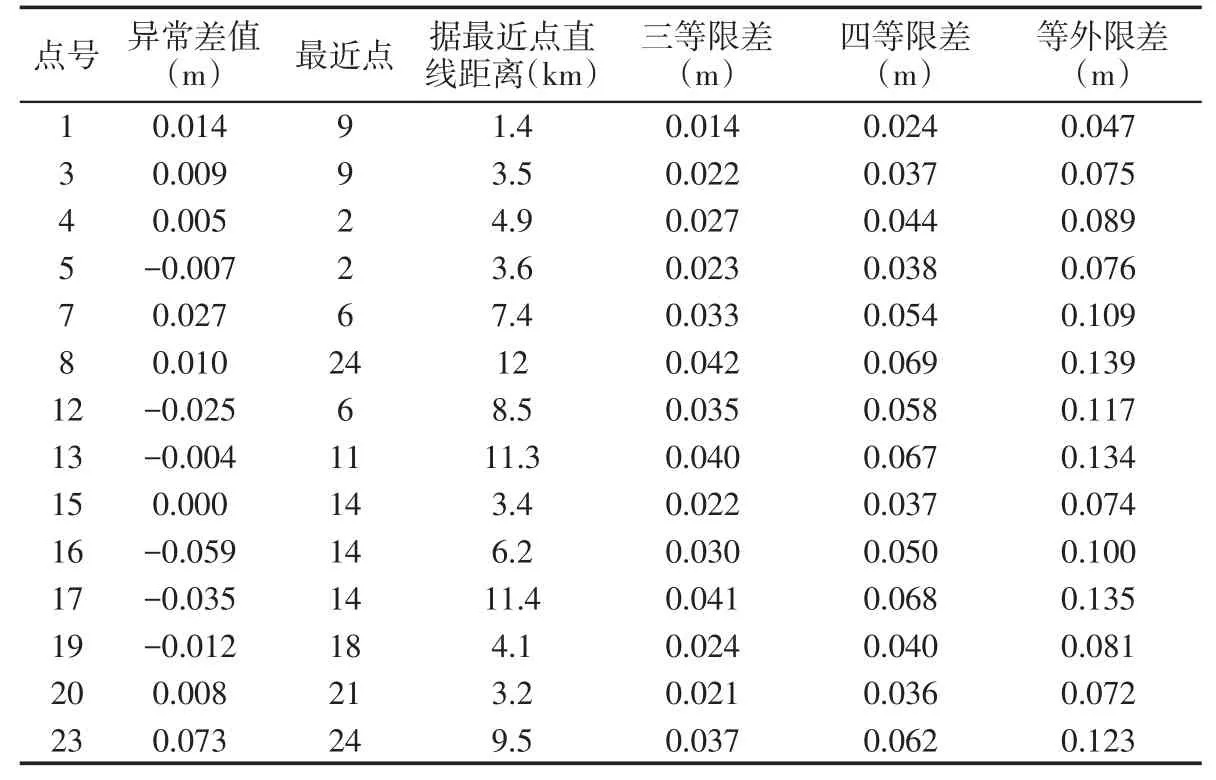
表4GNSS水準精度評定表Tab.4 GNSS benchmark accuracy evaluation

2.5 外圍點的精度評定

各種擬合模型都不宜外推，但在實際工作中，測區的GNSS點不可能全部都包含在已知點連成的幾何圖形內。對這些外圍點，GNSS水準計算時只能外推，為了校核GNSS水準外推精度，從1、9號點按三等水準測量精度要求聯測了3個水準點40、41、42，并對GNSS水準外推精度進行了校核。方案如圖4所示，圖4中帶三角形的點為擬合點，其他點為校核點，擬合區域東西長54 km，南北長28 km。從而得到了GNSS水準外圍點精度評定情況，如表5所示。

從表5中可以看出，擬合點東側區域外圍25 km的控制點差值均在四等限差范圍以內，南側外圍20 km的控制點均在等外限差以內，經分析可知，這是由于擬合區域東西向較南北向長，因此在同樣距離下，東側區域外側的精度較好。在四等限差精度限差的要求下，東側外推長長度比約為25/54≈1/3，在等外限差精度限差的要求下，南北側外推長度比約為20/28≈2/3。這個結論僅對本項目適用，要具體問題具體分析，在驗證合格后方可使用。

圖4GNSS水準外圍點精度估算控制點分布圖Fig.4 Distribution of GNSS benchmark peripheral point evaluation

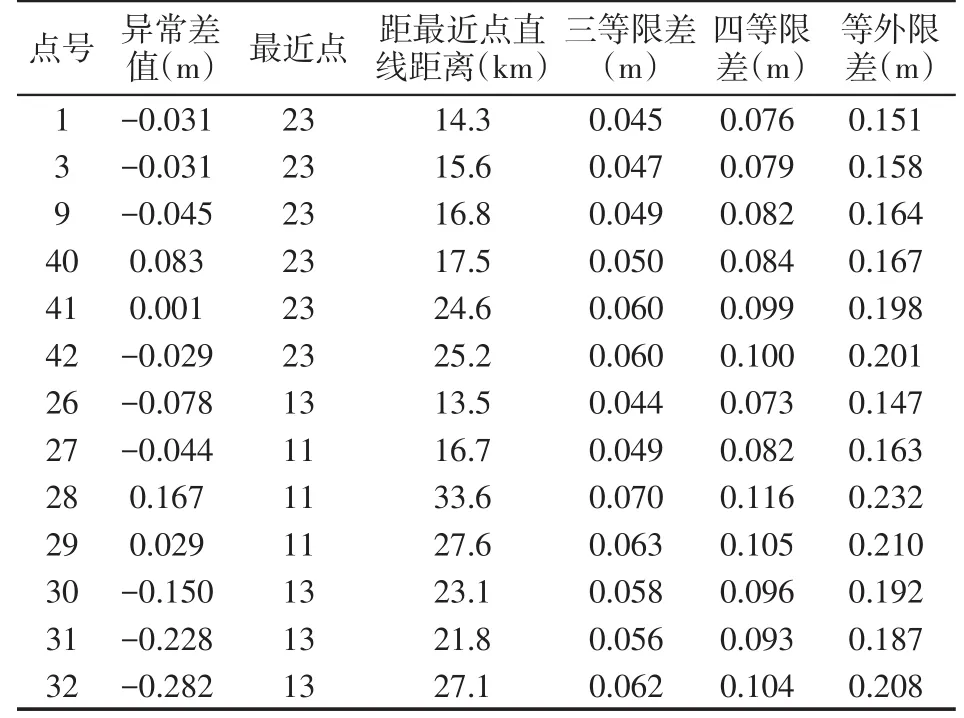
表5GNSS外圍點精度評定表Tab.5 GNSS benchmark peripheral point used for accuracy

3 結論

GNSS水準擬合的精度不僅與起算點的數量有關，而且與起算點的空間分布有著密切的關系，一般來說控制點數量越多，控制點分布越均勻，擬合精度越高；在面積較大的區域，建議采用分區擬合的方法進行擬合，各區之間要有公共點；在控制點密度足夠時，采用GNSS水準擬合可以滿足四等水準測量精度的需求；GNSS水準外圍點在擬合區域外圍1/3可以達到四等水準測量精度。但需要指出的是，GNSS擬合的精度與模型精度，區域高程異常變化的復雜程度有關，在應用GNSS水準擬合時，一定要有檢核，并且在檢核點精度滿足要求時方可使用。

［1］李征航，黃勁松.GPS測量與數據處理［M］.武漢：武漢大學出版社，2005.

［2］杜玉柱.GNSS測量技術［M］.武漢：武漢大學出版社，2013.

［3］楊小青，胡伍生.基于神經網絡的似大地水準面模型精化方法研究［J］.測繪工程，2008，17（4）：8-11. YANG X Q，HU W S.Research on the measures of accurating quasi geoid model based on Neural Network［J］.Engineering of Sur?veying and Mapping，2008，17（4）：8-11.

［4］焦明連.GPS?RTK高程擬合方法研究［J］.海洋測繪，2005，25（3）：6-11. JIAO M L.Research on the Data Fitting Method of GPS RTK Height［J］.Hydrographic Surveying and Charting，2005，25（3）：6-11.

［5］伍青云.GPS高程擬合的方式及可靠性分析［J］.現代測繪，2006，29（4）：29-31. WU Q Y.The Form of GPS Height Interpolation and Analysis of Safety［J］.Modern Surveying and Mapping，2006，29（4）：29-31.

［6］劉大杰，施一民，過靜珺.全球定位系統的原理與數據處理［M］.上海：同濟大學出版社，2006.

［7］胡伍生，高成發.GPS測量原理及其應用［M］.北京：人民交通出版社，2002.

［8］華錫生，黃騰.精密工程測量技術及應用［M］.南京：河海大學出版社，2002.

［9］奉光澤.GPS高程擬合精度的研究［J］.測繪學報，2008，31（6）：260-264. FENG G Z.Research on Fitting Precision of GPS Elevation［J］.Acta Geodaetica et Cartographica Sinica，2008，31（6）：260-264.

［10］雒養社，馬超.GPS擬合高程精度分析［J］.中國煤田地質，2007，19（3）：77-79. LUO Y S，MA C.Precision Analysis of GPS Elevation Fitting［J］.Coal Geology of CHINA，2007，19（3）：77-79.

［11］JTS131-2012，水運工程測量規范［S］.

Analysis on precision of GNSS level base on surface fitting in mountain area

FANG Xin?yu,LU Wei,YAO Xiao?wei
(Tianjin Research Institute for Water Transport Engineering,Surveying&Mapping Technology Research Center for Water Transport Engineering,Tianjin 300456,China)

The elevation systems in measurement and their transformation relationship were introduced,and the GNSS level models were also introduced briefly.The precision of GNSS leveling surface fitting in mountain area was analyzed through examples,and the GNSS level accuracy and peripheral point accuracy were assessed,and some valuable conclusions were obtained.

Global Navigation Satellite System;height fitting;normal height;geodetic height;fitting precision

P 715

A

1005-8443（2015）02-0176-05

臺州打造椒江內河樣板航道

2014-04-22；

2014-08-15

房新玉（1983-），男，河南省南陽人，工程師，主要從事GPS測量數據處理研究工作。

Biography：FANG Xin?yu（1983-），male，engineer.

本刊從浙江省交通運輸廳獲悉，2015年2月25日，浙江省臺州市椒江區組織開展了椒江內河樣板航道建設協議簽訂活動。椒江內河樣板航道位于臺州永寧河十字涇，起點為椒江與路橋行政區域交界，終點為洪家街道永寧河段，總長1.3 km，預計工程總投資約800萬元。據悉，該工程將由椒江區港航管理處負責實施，是臺州市進一步響應浙江省“五水共治”政策，不斷提高航道通航能力、美化兩岸環境、改善周邊居住條件、打造標準航段的重點工程。同時，該工程也是目前臺州市計劃建設的唯一的內河樣板航道。（殷缶，梅深）