Heston隨機波動率市場中帶VaR約束的最優投資策略

曹 原

(中國人民大學 財政金融學院，北京 100872)

?

Heston隨機波動率市場中帶VaR約束的最優投資策略

曹 原

(中國人民大學 財政金融學院，北京 100872)

本文研究了Heston隨機波動率市場下, 基于VaR約束下的動態最優投資組合問題。

假設Heston隨機波動率市場由一個無風險資產和一個風險資產構成,投資者的目標為最大化其終端的期望效用。與此同時, 投資者將動態地評估其待選的投資組合的VaR風險,并將其控制在一個可接受的范圍之內。本文在合理的假設下,使用動態規劃的方法,來求解該問題的最優投資策略。在特定的參數范圍內,利用數值方法計算出近似的最優投資策略和相應值函數, 并對結果進行了分析。

最優投資組合;Heston隨機波動率;動態VaR約束;動態規劃

0 引言

自從Markowiz的均值-方差理論奠定了現代數量金融的基礎以來,采用方差度量風險存在一定的不合理性,比如方差將高于均值的波動也計算為了風險,受到了眾多學者的質疑。近些年來,眾多新的風險評估指標如VaR(value at risk),CVaR(conditional value at risk), CaR(capital at risk), EaR(earning at risk)等都被廣泛地應用于理論研究和實踐中。

Basak and Shapiro[2]用鞅方法研究了常數VaR約束下的最優投資組合問題。Cuoco and He[3]利用動態規劃的方法來求解動態再評估(reevaluated)的VaR和TCE (tail conditional expectation)約束下的最優投資組合。所謂動態再評估方法,即在每個交易期對風險進行持續的評估,并要求其始終處于一個合理的范圍之內,我們稱之為動態的VaR約束。此外,Yiu[4]分析了動態VaR約束下的最優投資消費問題,并且利用數值方法給出了最優策略和值函數的近似解。

在實際金融實務中,大多數金融機構在每個交易日都至少重新對投資組合進行一次風險評估*1995年4月的巴塞爾提案提出，要求銀行等金融機構至少每日重新評估它們的VaR風險，且對資產要求設定為之前60個工作的日均VaR的最大值。說見Jorion(2001)pp.64- 65.;此外,若風險約束僅僅是初始時刻選定的一個常數,將出現如Cuoco and He[3]文中指出的財富較少時,約束條件無效的情況發生,所以取隨時間和財富變化的風險上限更為合理。

近年來,一些學者拓展了Black-Scholes 模型,提出了多種更為貼近現實的隨機波動率模型,如Stein and Stein[5]提出的Stein-Stein模型;Heston[6]提出的Heston模型。同時,一些學者基于以上隨機波動率模型,研究了在對應金融市場下的最優投資問題。例如, Liu and Pan[7]研究了波動率滿足Heston模型時含衍生產品的金融市場的最優資產配置問題;Chacko and Viceira[8]在Heston波動模型下最優投資-消費問題的顯式解;Hsuku[9]考慮了具有連續時間遞歸偏好效用的投資者在帶非冗余的衍生證券的Heston隨機波動率市場中的最優投資組合問題,并得到了最優投資策略在特殊參數下的解析式與一般情形下的數值解。伊博等[10]研究了Heston隨機波動率市場中的最優收斂策略問題, 并考慮了在有限賣空約束下投資者的最優投資問題。

綜合以上兩方面,有些學者同時研究了隨機波動率市場中帶VaR約束的最優投資問題,例如,Pirvu[11]研究了系數隨機的金融市場中,帶動態VaR約束的投資組合問題。他利用Ito積分的鞅性及對數效用函數的特殊性質,將隨機控制問題轉化為確定性問題進行求解。李仲飛和李克勉[12]引入了非冗余的衍生證券將市場完備化,使用類似于Pirvu[11]的方法,求出了在Heston隨機波動率模型下,受動態VaR風險約束時,投資者的最優資產配置策略。伊博等[13]研究了Stein-Stein 隨機波動率模型下,帶VaR約束的最優投資問題,并得到了在該假設下,投資者最優投資策略及相應值函數的顯式解。

就我們所知,目前還沒有文獻在CRRA效用函數體系下,同時考慮具有動態VaR風險約束與Heston隨機波動率的金融市場中的最優投資問題。這主要因為,Heston隨機波動率市場中帶動態VaR約束的最優投資策略無法求出顯式解,必須依賴于數值方法進行近似計算。本文擬在現有文獻的基礎上,同時考慮動態VaR約束和Heston隨機波動率兩重要因素。假設最大化終端財富的期望冪效用為投資者的目標,風險資產價格過程服從Heston模型。本文研究受動態VaR約束下的最優投資組合問題,并運用動態規劃原理結合Yiu[4]提出的數值方法,近似地求得投資者的最優投資策略和值函數。

本文結構如下:第二部分描述Heston隨機波動的金融市場的數學模型。第三部分回顧無約束時的最優投資組合問題。第四部分定義動態VaR約束。第五部分推導了最優投資策略。第六部分給出數值算法和相應計算結果及相關經濟含義。第七部分是總結。

1 市場模型

我們考慮如下的隨機波動率市場,[0,T]是其有限交易區間, 給定完備的賦流概率空間(Ω,F,{Ft},P),其中{Ft}是布朗運動Zs(t),Zυ(t)生成的自然域流。假設投資者可投資于兩種金融資產:一種是無風險資產,如債券,其價格過程B(t)滿足

dB(t)=B(t)rdt,B(0)=B0

(1)

其中r>0, 表示無風險利率; 另一種是風險資產, 如股票, 其價格過程S(t)將滿足如下Heston模型

(2)

風險資產價格的波動率為V(t), 其中V(t) 滿足一個均值-回復過程

(3)

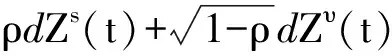
(4)

其中W0為初始財富。

2 無VaR約束時的最優資產配置

不考慮VaR約束, 假設投資者具有如下的效用函數

(5)

常數γ是投資者的相對風險厭惡系數, 其中Et[·]=E[·|Ft],γ∈(0,1)∪(1,+∞)，W(T), 是投資者的終端財富. 在隨機的投資機會集下, 定義該問題的最優值函數為

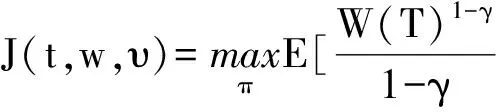
(6)

根據Bellman原理, 相應的Hamilton-Jacobi-Bellman(HJB)方程為

(7)

定理1 當投資者不考慮VaR約束問題下,其在Heston隨機波動率市場中,最優投資策略如下:

值函數有如下形式,

(8)

其中

(9)

(10)

(11)

(12)

3 動態VaR約束

在無約束情形下, 最優投資組合問題存在解析解.但更為實際的情況是, 投資者將會評估其投資風險, 將其投資策略限制在一個可以接受的風險承受范圍之內.類似于Cuoco and He定義t 時刻的動態VaR如下

VaRtα,π=inf{L≥0:P(exp(τr)Wπ(t)-Wπ(t+τ)≥L|Ft)<α}

(13)

其中1-α為給定的置信水平，可以這樣理解該定義:在事先給定的置信水平下,τ時間內財富損失的最大值。為避免繁瑣的討論,假定α<0.5。

根據財富方程可得

(14)

考慮時間區間[t,t+τ],類似可得到

(15)

根據Pirvu,在很短時間τ內, 忽略π(t)和V(t) 的變化,于是

(16)

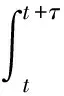
(17)

其中N-1(α)為正態分布的α分位數,x+=max(0,x)。由于在受約束情形下,對投資于風險資產的比例進行了限制,導致原先的最優投資策略在此未必是可行的,將定理1中的最優策略代入,如下情形將不會受VaR約束:

(18)

其中W0為初始財富。

4 最優性條件

我們利用動態規劃方法求解以上帶VaR約束的最優化問題,值函數可寫為

(19)

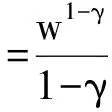
(20)

利用Langrage函數法,將約束條件引入HJB方程

(21)

由一階條件和Kuhn-Tucker條件,我們得到如下的最優性條件:

(22)

(23)

λ≤0

(24)

從中可以求出最優策略π*和λ*。

5 數值算例

在第三部分中,我們得到了無約束情形下的值函數的解析式。當VaR約束被附加的時候,假設值函數具有如下形式:

(25)

H和h的形式將不僅僅依賴于時間t,而同時依賴于狀態變量w,υ。但是我們在后面的數值算例中會發現,對于某些合理的參數而言,H,h關于狀態變量w,υ的變化是微小的。根據動態規劃原理,最優化條件可寫為:

(26)

其邊界條件為

(27)

其中

(28)

將假設的值函數形式代入HJB方程,整理后,我們得到如下兩個方程:

γht+(1-γ)γ+γκηH=0

(29)

我們假設非限制問題的解為我們迭代算法的初始解,將w,υ,t離散化為Nw×Nυ×Nt個格點,我們計算值函數的算法如下:

步驟2 對于w=[0,Δw,……,NwΔw],υ=[0,Δυ,……,NυΔυ],t=[0,Δt,……,Nt-1Δt,T],判定

(30)

若成立,取πk+1=πk,若不然求解

(31)

(32)

解出λk+1,πk+1。

步驟3 對于w=[0,Δw,……,NwΔw],n=Nt,Nt-1,……,0 解

(33)

步驟4 回到步驟2, 并取k=k+1直到收斂。

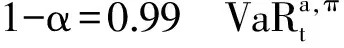
圖1 H關于波動率v的變化趨勢

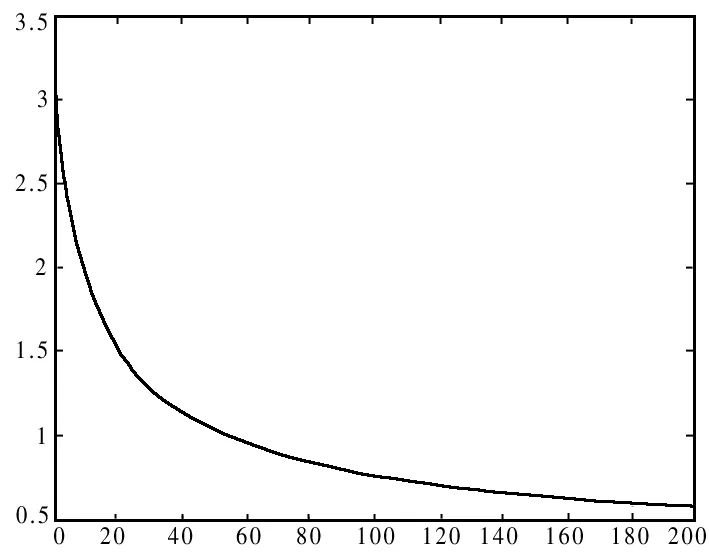
圖2 H關于財富率w的變化趨勢

圖3 h關于波動率v的變化趨勢

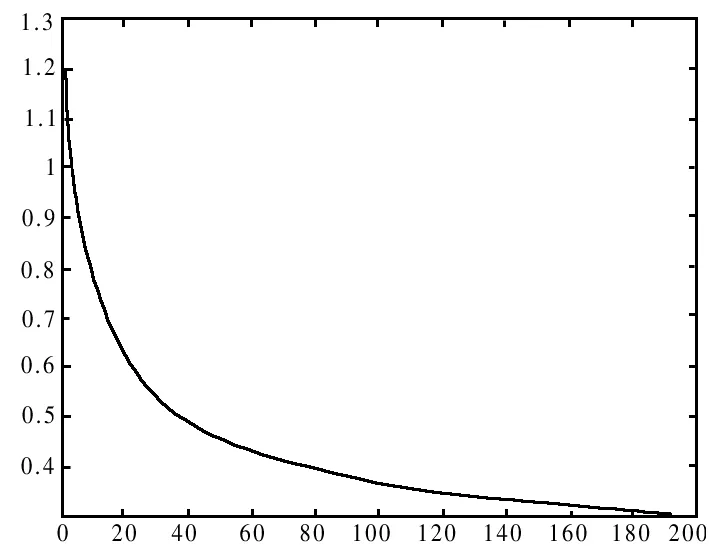
圖4 h關于財富率w的變化趨勢

圖5 最優投資策略關于剩余投資時間T-t的變化趨勢

6 總結和展望

隨著量化金融方法在實務操作中使用越來越頻繁,對量化的精確性也提出了越來越高的要求。 實證研究已經證實:現實金融市場的波動率在一般情形下并不是一個常數,而應滿足一個隨機變量。Heston隨機波動率假設作為全局隨機波動率中最主流的觀點,已經在學界和業界被廣泛采用,故而研究Heston隨機波動率市場中的最優投資組合問題給實務操作者提供了更為準確的量化投資輔助。另一方面,無論對于機構投資者或者個人投資者來說,控制其投資組合的風險都應作為他們投資金融市場的基本需求。甚至對于金融市場監管者,為了維護金融市場穩定和大多數投資者利益,也應對大型投資者(主要為機構投資者)的投資組合進行一定的限制。基于現實中的實際要求,研究被廣泛采用的VaR約束頗具實用價值,并為金融市場風險管理提供了相應的理論支持。因此本文結合兩方面,研究了金融市場滿足Heston隨機波動率模型時,帶動態VaR約束的最優投資組合選擇問題,利用動態規劃和數值方法,在一定的參數條件下,近似地解出了最優投資策略并給出了數值算例。但是, 本文的方法需要對參數施加一些限制,即需要當前財富始終處于一個較高的水平,并非適用于所有的參數,故而對大型投資者尤其機構投資者,會具有更大的指導意義。對于更廣泛的參數,還需要探索更為普遍的算法。

[1] Markowitz H M. Portfolio selection[J]. Journal of Finance, 1952, (7): 77-91.

[2] Basak S, Shapiro A. Value-at-risk-based risk management: optimal policies and asset prices[J]. The Review of Financial Studies, 2001, 14(2): 371- 405.

[3] Cuoco D, He H, Issaenko S. Optimal dynamic trading strategies with risk limits[J]. Operational Research, 2008,56(2): 358-368.

[4] Yiu K F C. Optimal portfolios under a value-at-risk constraint[J]. Journal of Economic Dynamics& Control, 2004, 28: 1317-1334.

[5] Stein E M, Stein J C. Stock price distributions with stochastic volatility: an analytic approach[J]. Review of Financial Studies, 1991, 4: 725-752.

[6] Heston S L. A closed-form solution for options with stochastic volatility with applications to bond and currency options[J]. Review of Financial Studies, 1993, 6: 327-343.

[7] Liu J, Pan J. Dynamic derivative strategies[J]. Journal of Financial Economics, 203, 69: 401- 430.

[8] Chacko G, Viceira L M. Dynamic consumption and portfolio choice with stochastic volatility in incomplete markets[J]. Review of Financial Studies, 2005, 18: 1369-1402.

[9] Hsuku Y. Dynamic consumption and asset allocation with derivative securities[J]. Quantitative Finance, 2007, 7(2): 137-149.

[10] 伊博,李仲飛,曾燕.隨機波動率市場存在股票誤價時的最優投資策略[J].應用概率統計,2013,29(3):261-274.

[11] Pirvu T A. Portfolio optimization under the value-at-risk constraint[J]. Quantitative Finance, 2007, 7: 125-136.

[12] 李仲飛,李克勉.動態VaR約束下帶隨機波動的衍生證券最優投資策略[J].中山大學學報(社會科學版),2010,50(3):184-192.

[13] 伊博,李仲飛,曾燕.基于動態VaR約束與隨機波動率模型的最優投資策略[J].運籌學學報,2012,16(2):77-90.

[14] Jorion P, 2001. Value at risk[M]. Mcgraw-Hill. New york.

Optimal Inverstment Strategy with Heston Stochastic Volatility and Dynamicvar Constraint

CAO Yuan

(TheSchoolofFinance,RenminUniversityofChina,Beijing100872,China)

This paper considers an optimal portfolio choice problem under Heston stochastic volatility model and a dynamic VaR constraint. Assume the financial market consists of one risky asset, like stock, whose price satisfies a Heston stochastic volatility model and one risk-free asset, like bond. The investor aims to maximize the expected power utility of the terminal wealth. At the same time, the investor hopes to manage the portfolio risk by a dynamic VaR constraint, which means she will compute the VaR of her portfolio continually. Using the stochastic dynamic programming approach, we solve the problem numerically. Finally, economic implications are proposed to illustrate the impacts of Heston stochastic volatility and dynamic VaR constraint on the investor’s optimal strategy. Our numerical experiment shows that the dynamic VaR criterion is an effective tool to manage the risk during the whole investment period.

portfolio optimization; Heston stochastic volatility; dynamic VaR constraint; dynamic programming approach.

2013- 07-14

曹原(1989-)，女，江西南昌人，博士，研究方向：金融學。

F380

A

1007-3221(2015)01- 0231- 06