塔機吊臂最危險回轉角度的探討
李 蕾,李志剛
(1.山東國弘重工機械有限公司,山東 淄博 256401;2.中建三局集團有限公司總承包公司山東分公司,山東 青島 266100)
塔機吊臂最危險回轉角度的探討
李 蕾1,李志剛2
(1.山東國弘重工機械有限公司,山東 淄博 256401;2.中建三局集團有限公司總承包公司山東分公司,山東 青島 266100)
從塔身的強度、剛度和穩定性三個角度出發,尋求塔身的最危險工況,論證了起重平面相對塔身的最危險角度,為塔身的設計提供了依據,也為整機有限元的建模方式提供了參考。
塔式起重機;塔身;吊臂;回轉角度;有限元
塔身是塔式起重機(以下簡稱“塔機”)的重要組成部分,起著架高、支撐的作用,承受巨大壓力和彎矩,塔身的強度、剛度和穩定性直接影響整機的安全可靠性,因此塔身最危險的設計工況的確定顯得尤其重要。
1 塔身的彎曲強度隨吊臂回轉角度的變化規律
如圖1所示,起重臂繞塔身中心旋轉一個角度θ,那么塔身截面在起重臂方向的截面特性如下。
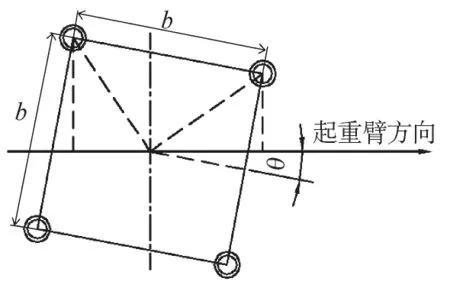
圖1 塔身與起重臂的相對位置
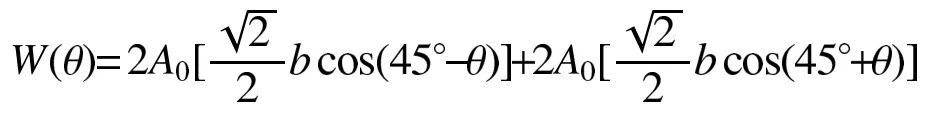
經推導得
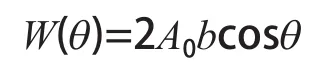
其中,A0為每根主肢的面積;b為相鄰兩根主肢的形心距離。
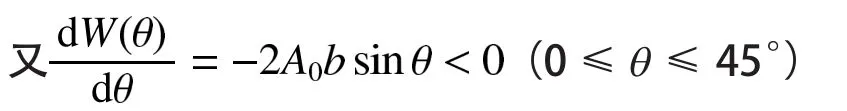
當θ=0°時,W(θ)最大,即彎曲強度最高,此時W(θ)=2A0b。
由此可以得出推論:僅受彎矩時,θ=45°的工況比θ=0°的工況危險倍。
2 塔身剛度隨吊臂回轉角度的變化規律
塔身剛度用EI表示,彈性模量E與圖1中的角度θ無關,而繞起重臂方向的慣性矩如下。

因此慣性矩I(θ)與θ無關,即塔身的剛度EI不隨角度θ的變化而變化。
3 塔身穩定性能隨吊臂回轉角度的變化規律
用桿件的長細比λ作為衡量塔身穩定性的指標,如式(1)所示。

公式(1)中,計算長度l與圖1中的θ無關,而回轉半徑r就可以作為衡量穩定性的指標,如公式(2)所示。

將慣性矩公式代入式(2),得

因此,回轉半徑r也是不隨θ的變化而變化,即塔身穩定性與θ的變化也無關。
4 有限元法驗證
以某公司研發的QTZ315(7040)塔身為例,用有限元法來驗證本文的結論。有限元模型如圖2所示。

圖2 不同θ的塔身有限元模型
4.1 只考慮彎矩的有限元驗證
只給塔身頂端施加來自頂端的滿載彎矩M,其中M=315/2=157.5tm,其計算結果如表1所示。
1)結果的強度分析:由于本文的推論是建立在彎曲理論中的平面假設基礎上,即假設塔身的每一個整截面形狀是嚴格保持不變的,而且永遠垂直于塔身軸線,塔身主肢幾乎沒有自己的彎曲變形,從而使得主肢沒有彎曲應力,只有軸向應力,因此為了有可比性,應該把軸向應力作為一項重要的驗證方面。
由表1可知,梁單元的軸向最大軸向應力σN隨著θ的增加而增加,θ為45°時σN最大,設為σN-45,并且,正好驗證了本文的推論之一,即θ=45°的工況比θ=0的工況危險倍。
然而,由于塔身實際是格構式結構,即塔身主肢有自己的變形和彎曲應力,因此為了趨近實際情形,還需將綜合應力(最危險的應力組合)作為一項驗證方面。
由表1可知,梁單元的最大綜合應力σmax同樣隨著θ的增加而增加,θ為45°時σmax最大,設為,并且,比推論的結果稍小,就是因為主肢的彎曲。
2)結果的剛度分析:由表1也可以看出,隨著θ的變化,其撓度變化微乎其微,之所以有變化,是因為推導塔身的慣性矩公式的時候,做了近似處理,才使得其值看似恒量。
4.2 同時考慮彎矩、頂端壓力和自身重力的有限元模擬
施加的載荷:來自塔身頂端的滿載彎矩M=315/2=157.5tm、塔身以上所有部件和最大起重量產生的壓力N=774 974N,并且施加重力,其計算結果如表2所示。
由表2可知,梁單元的最大軸向應力σN隨著θ的增加而增加,θ為45°時σN最大,設為,
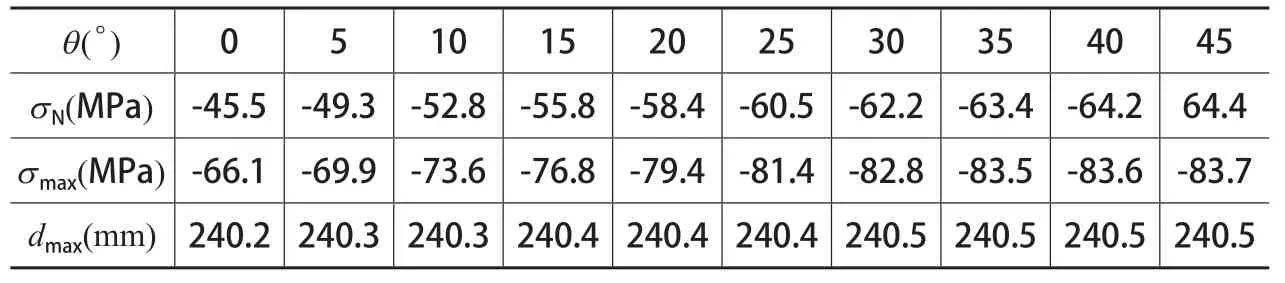
表1 只考慮彎矩的有限元計算結果

表2 同時考慮彎矩、頂端壓力和自身重力的有限元計算結果
并且σ2N-45/σ2N-0=1.25,最大綜合應力σmax同樣隨著θ的增加而增加,θ在45°附近時σmax最大,設為σ3N-45,并且σ3N-45/σ3N-0=1.16。即該塔身在滿載的時候,θ=45°的工況比θ=0的工況危險1.16倍。
5 結 論
本文通過理論論證和一個實例的有限元計算驗證,得出以下結論。
塔身的剛度和穩定性不隨夾角θ的變化而變化,而塔身的強度則隨θ變化,而且當θ=45°時,強度最弱,危險性可增加至1.2倍。因此塔身最危險的工況應該是吊臂軸線平行于塔身對角線的情形,在建立塔機有限元模型的時候應尤其注意。
[1]GB/T 3811—2008,起重機設計規范[S].
[2]GB/T 13752—1992,塔式起重機設計規范[S].
[3]GB/T 5031—2008, 塔式起重機[S].
(編輯 賈澤輝)
Discussion on the most dangerous of tower crane jib rotating angle
LI Lei, LI Zhi-gang
TH212;TH213.3
B
1001-1366(2015)01-0046-02
2014-11-03

