船用柴油機氣缸套幾何誤差在線測量技術研究

蘇世杰，代永俊，李欽奉，唐文獻

（江蘇科技大學機械工程學院，江蘇鎮江212003）

船用柴油機氣缸套幾何誤差在線測量技術研究

蘇世杰，代永俊，李欽奉，唐文獻

（江蘇科技大學機械工程學院，江蘇鎮江212003）

設計一套船用柴油機氣缸套幾何誤差在線測量系統，分析機床定位誤差、傳感器安裝及測量誤差對缸套表面各被測點坐標計算準確度的影響，建立測量誤差計算數學模型。基于非線性規劃方法建立缸套直線度誤差、圓度誤差、圓柱度誤差的評定數學模型，通過與現有測量數據及誤差評定模型的對比分析，表明該模型評定準確度較高。搭建在線測量原型系統，并進行測量實驗，實驗數據表明該系統具有結構簡單、檢測準確度及檢測效率高等特點。

船用柴油機氣缸套；幾何誤差；在線測量；非線性規劃

幾何誤差的測量主要分為接觸式測量和非接觸式測量，接觸式測量常采用三點法、兩步法、多步法[2-4]等，但只適合于小直徑工件，且效率低、受人為因素影響較大。隨著光電技術的發展，非接觸式測量逐漸得到了廣泛應用。張振久[5]提出了一種基于激光跟蹤儀的轉臺系統幾何誤差檢測方法。鄭宇[6]對大型圓柱件圓柱度誤差測量方法進行了研究。羅小燕[7]研制了一種大型回轉類零件幾何誤差測量系統。Chou[8]采用三坐標測量機及輔助計算機系統組成的高準確度測量儀對圓柱形工件的幾何誤差進行測量。

本文提出一種船用柴油機氣缸套幾何誤差在線測量方法，建立基于非線性優化方法的氣缸套幾何誤差評定數學模型。完成了某型氣缸套的直線度、圓度及圓柱度的在線測量實驗，并與在三坐標測量機上的測量結果進行了對比分析，結果表明該原型系統測量精度及誤差評定準確度較高。

1 氣缸套幾何誤差在線測量系統

1.1 系統總體結構

本文設計的在線測量系統的基本原理是：首先在數控立車的刀架上安裝激光位移傳感器；根據待測幾何誤差項目規劃所需測量點的空間坐標，并通過計算機生成對應測量程序；接著將測量程序輸入數控立車控制系統，由測量程序同步控制數控立車的運動及激光位移傳感器的觸發采樣；然后在計算機中根據預設參數和模型將傳感器的采樣值與數控立車的當前坐標值融合以得到缸套表面各點坐標；最后采用建立的氣缸套幾何誤差評定數學模型，實現對氣缸套幾何誤差的計算。

測量系統包括數控立車、高準確度激光位移傳感器及控制器、磁力底座、測試系統，總體結構如圖1所示。在船用柴油機氣缸套加工完成后，拆下刀架上的刀具，將安裝有高準確度激光位移傳感器的磁力底座吸附在刀架上，測試系統分別與數控系統和傳感器控制器相連，并通過RS232接口進行通信，而高準確度激光位移傳感器控制器的采樣觸發端子與數控系統PLC的開關量輸出端子連接。

1.2 在線測量流程

如圖2所示，船用柴油機氣缸套的幾何誤差在線測量具體流程如下：

1）在測試系統中輸入測量參數并生成測量程序（G代碼），接著通過通信接口將測量程序發送至數控系統。以直線度為例，部分測量程序（G代碼）如下：

N20 G00 X0 Z100；將傳感器移動到初始位置。

N30 X440 Z0；將傳感器移動到缸套內壁。

N40 G04 U2；在測量點暫停2 s。

N50 M56；特殊M指令，向傳感器發出采樣觸發信號。

N60 Z-50；移動到下一點。

……

2）數控立車根據測量程序控制氣缸套及安裝于刀架上的激光位移傳感器運動；當激光位移傳感器運動到每一預定的測量點時，數控系統會執行預定義的特殊M指令，控制數控系統PLC的某一特定開關量輸出端子導通，向傳感器控制器的采樣觸發端子發出觸發信號；傳感器控制器控制激光位移傳感器進行一次采樣，獲得激光位移傳感器到氣缸套內壁的垂直距離，并將該距離數據發送至測試系統。

3）測試系統根據測量程序計算出傳感器在各測量點時的理論坐標（x′，z′，α），再結合步驟2）獲得的傳感器到氣缸套內壁的垂直距離l計算出各測量點的實際坐標（x，y，z），其計算公式為

式中：x′、z′——立車工件坐標系坐標；

α——立車工作臺的旋轉角度。

4）當測量完成后，將步驟3）計算得到的各測量點的實際坐標代入相應的誤差評定數學模型，最終計算出所需的幾何誤差值。

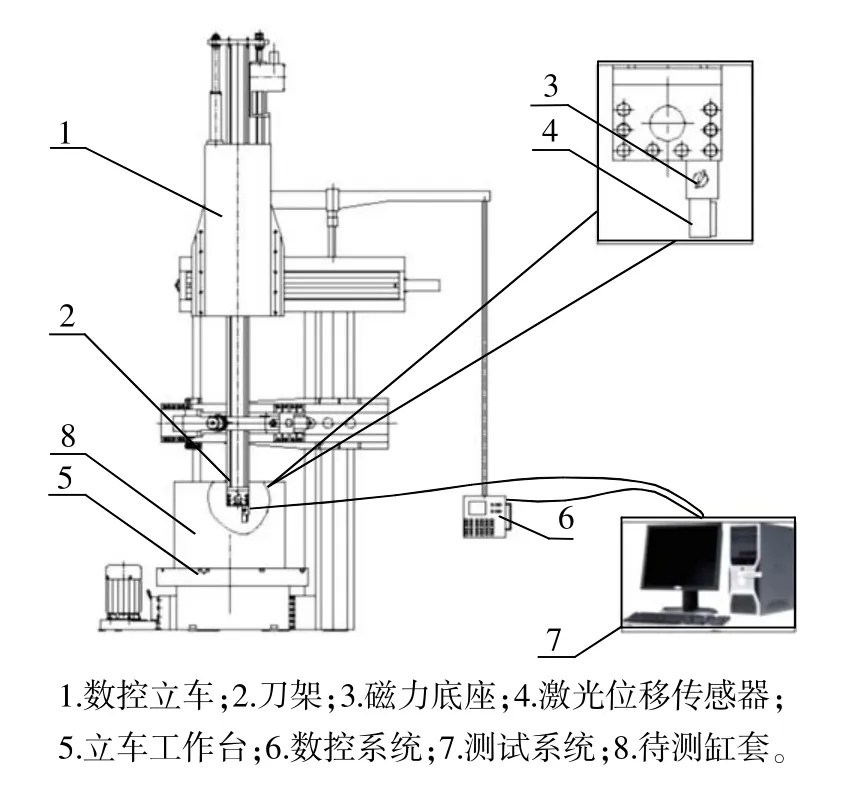
圖1 在線測量系統總體結構

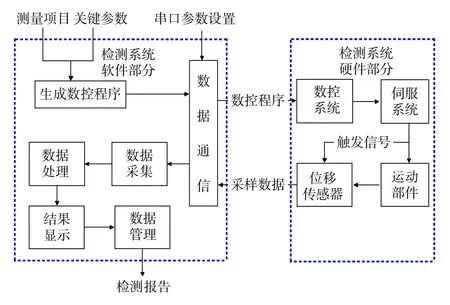
圖2 在線測量系統流程框圖

5）對結果進行顯示，并統一管理，生成檢測報告。

2 測量誤差分析

2.1 數控立車誤差

數控立車的定位準確度是指立車的運動部件在數控系統的控制下運動時所能達到的位置準確度[9-10]。設數控立車X軸定位誤差為、Z軸定位誤差為、C軸旋轉定位誤差為。在進行缸套直線度測量時，由于C軸靜止，故C軸旋轉定位誤差對測量結果沒有影響；在進行缸套圓度、圓柱度測量時，C軸的旋轉定位誤差只會導致圓周上的實際采樣點與理論采樣點產生角度偏差，對于測量結果也不產生影響。綜上所述，立車定位誤差所產生的測量誤差為

式中α為當前測量點的角度，對于直線度而言，始終為0；對于圓度、圓柱度而言，其值在0～360°變化。

2.2 激光位移傳感器誤差

激光位移傳感器的誤差來源包括安裝誤差和自身測量誤差兩方面，而安裝誤差又分為水平方向誤差和豎直方向誤差，下面從這兩方面進行分析。

2.2.1 傳感器水平安裝誤差分析

如圖3所示，激光位移傳感器安裝時可能在水平方向產生一個偏角β，造成傳感器的采樣點由缸套上的B1點移動到B2點，產生的水平偏角β=∠B1AB2。

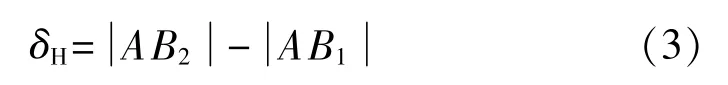
式中

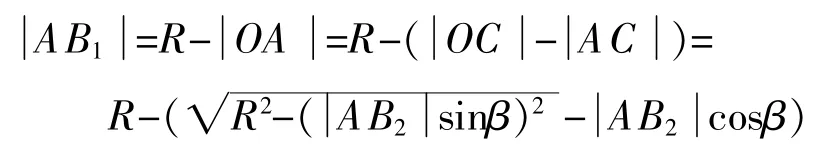
故

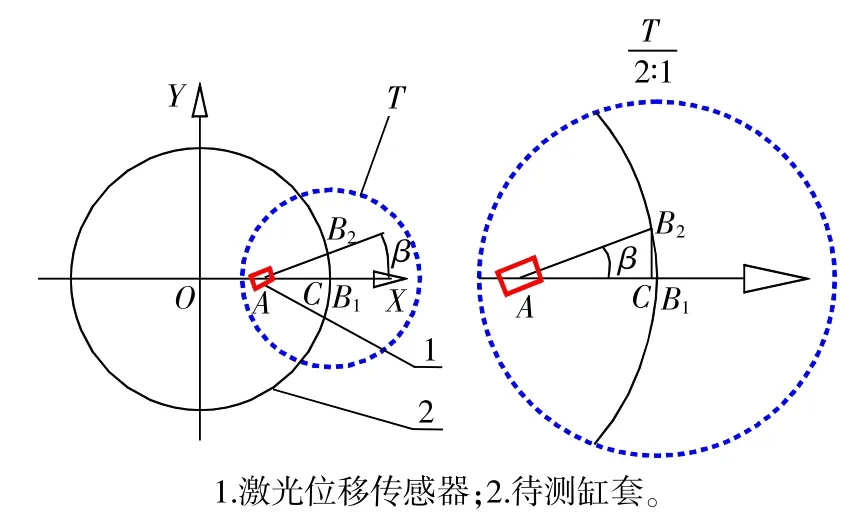
圖3 激光位移傳感器水平安裝誤差示意圖

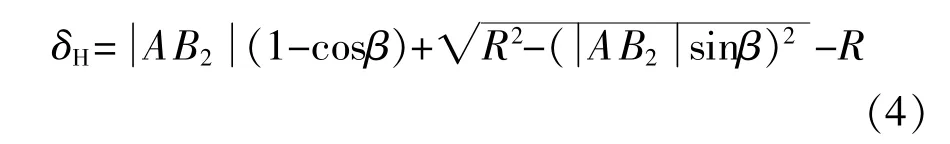
2.2.2 傳感器豎直安裝誤差分析

如圖4所示，激光位移傳感器安裝時可能在豎直方向產生一個偏角γ，造成位移傳感器的采樣點由缸套上的B1點移動到B2點，故豎直偏角γ=∠B1AB2。

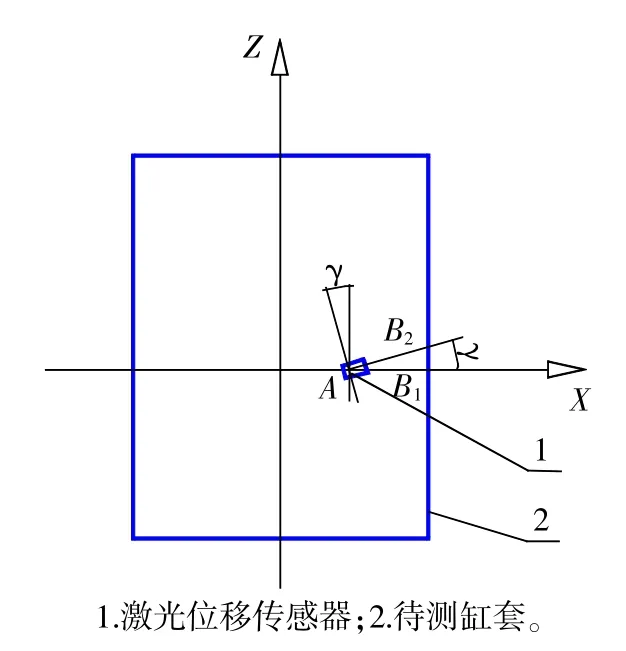
圖4 激光位移傳感器豎直安裝誤差示意圖

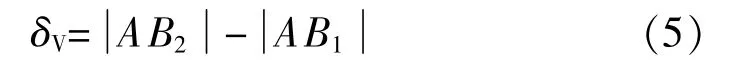
式中

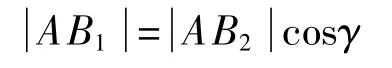
故

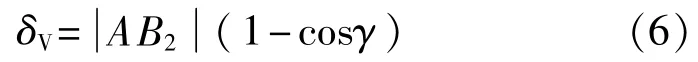
2.2.3 傳感器綜合誤差分析

由于傳感器水平方向安裝誤差δH和豎直方向安裝誤差δV處于兩個垂直平面內，且測量誤差δT會直接疊加到δH和δV上，則傳感器綜合誤差δS為

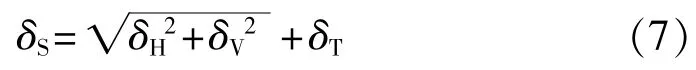
2.3 綜合測量誤差分析

綜合測量誤差需要同時考慮數控立車定位誤差和激光位移傳感器誤差，根據測量點坐標計算公式，綜合測量誤差為

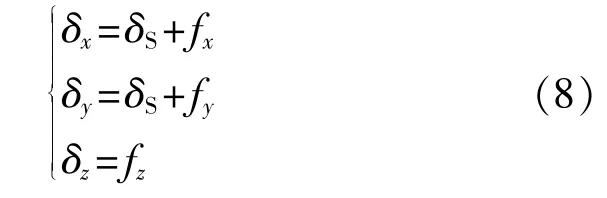
在實際使用過程中，由于刀架和磁力底座的準確度較高，故可保證激光位移傳感器的水平和豎直安裝偏角均在0.5°以內。針對直徑為φ500mm的某型船用柴油機氣缸套，本文使用CK5723×2500/1單柱數控立式車床，其X軸的定位準確度為f′x=0.004mm、Z軸的定位準確度為f′z=0.004mm；選用基恩士IL-030激光位移傳感器，其測量范圍為20～45mm，測量誤差δT為0.002mm。將以上各值分別帶入式（2）～式（8）可得：δx=0.008mm、δy=0.008mm、δz=0.004mm。

3 幾何誤差評定數學模型建立

幾何誤差的評定方法有多種，如最小區域法、最小二乘法、貼切法和簡易法等[11]。但這些方法存在著計算準確度不高或計算效率低等問題。下面討論采用多變量有約束非線性規劃算法[12]來建立缸套的幾何誤差評定數學模型，其標準形式為

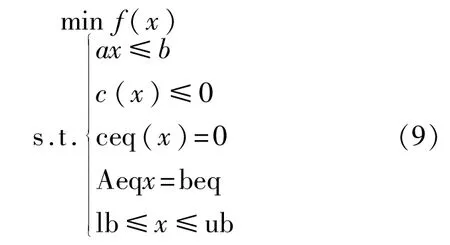
式中：x——自變量；

f（x）——目標函數；

ax≤b——線性不等式約束；

c（x）≤0——非線性不等式約束；

ceq（x）=0——非線性等式約束；

Aeq x=beq——線性等式約束；

lb≤x≤ub——變量上下限約束。

3.1 基于非線性規劃方法的直線度評定模型

直線度誤差是指實際直線相對于理想直線的變動量，理想直線的位置應符合最小條件。故可假定理想直線的方程為z=ax+b。則必定存在兩條與理想直線平行的直線，這兩條平行直線截距差最小，且所有測量點均在這兩條直線之間。可建立如下所示的直線度評定數學模型：

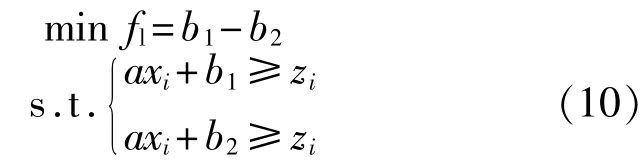
式中：min fl——氣缸套直線度計算目標函數；

（xi，zi）——各測量點的實際坐標值；

a——兩平行直線的斜率；

b1、b2——兩平行直線的截距。

3.2 基于非線性規劃方法的圓度數學模型建立

圓度誤差是指在回轉體的某一橫截面內被測實際圓相對于理想圓的變動量，理想圓的選擇應使變動量最小。故可假定理想圓的方程為

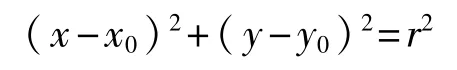
式中：（x0，y0）——理想圓的圓心坐標；

r——理想圓的半徑。

則必定存在兩個與理想圓同心的圓，這兩個同心圓的半徑差最小，且所有測量點均在這兩個圓之間。可建立如下所示的圓度評定數學模型：

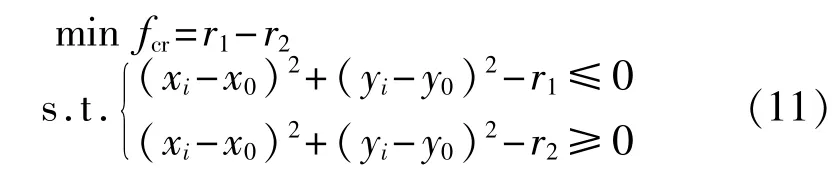
式中：min fcr——氣缸套圓度計算目標函數；

（xi，yi）——各測量點的實際坐標值；

r1，r2——兩同心圓的外圓半徑和內圓半徑；

（x0，y0）——兩同心圓的圓心坐標。

3.3 基于非線性規劃的圓柱度數學模型建立

圓柱度誤差是指實際圓柱面要素對其理想圓柱面的變動量，理想圓柱面的選擇應使變動量最小。故可假定理想圓柱面上任意一點到圓柱中心線的距離為h，則必定存在兩個與理想圓柱同軸的圓柱，這兩個圓柱的半徑差最小，且所有測量點均在這兩個圓柱之間。可建立如下所示的圓柱度評定數學模型：

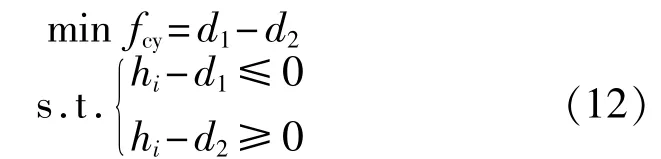
式中：min fcy——氣缸套圓柱度計算目標函數；

d1、d2——兩同軸圓柱面的外圓柱半徑和內圓柱半徑；

hi——各測量點到理想圓柱軸線的距離，可由海倫公式計算得到。

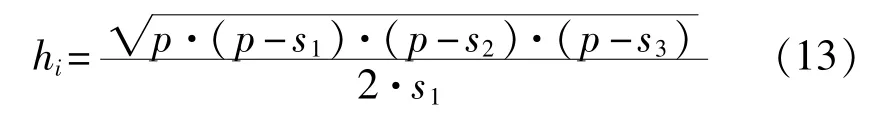
其中

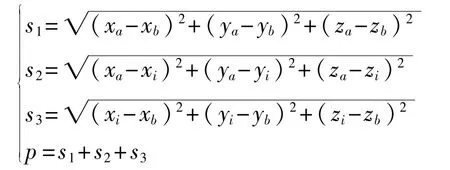
式中：（xa，ya，za）、（xb，yb，zb）——理想圓柱軸線上的兩點坐標；

（xi，yi，zi）——各測量點的空間坐標；

s1、s2、s3——軸線上兩點A、B和任一測量點組成的三角形的3條邊的邊長；

p——三角形的周長。

4 測量實驗及結果分析

4.1 誤差評定模型計算結果對比分析

目前常用最小二乘法進行幾何誤差的評定，也有學者提出用遺傳算法、粒子群算法等進行幾何誤差的評定[11，13-14]。本文利用現有文獻[13-14]的測量數據（見表1），采用上述模型對直線度、圓度及圓柱度進行誤差評定，評定結果的對比如表2所示。

結果分析：采用最小二乘法進行計算時，由于算法本身的局限性不可避免的會產生誤差；最優函數法相較于最小二乘法在準確度方面有一定的提高；本文提出的基于非線性規劃方法建立的誤差評定數學模型，其評定準確度比最優函數法有進一步的提高，且數學模型結構簡單、其幾何含義與國標提出的最小區域要求完全一致。

表1 文獻原始數據 mm

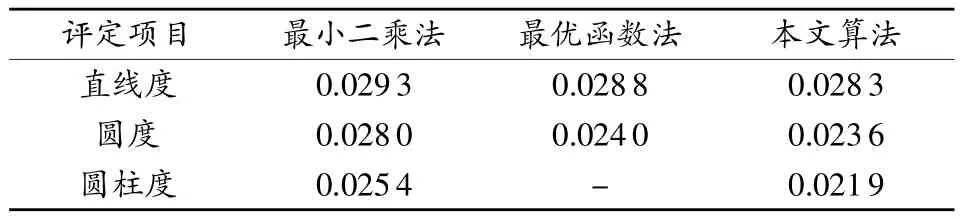
表2 3種幾何誤差評定結果比較 mm

4.2 測量實驗對比分析

為驗證整體方案的有效性，本文按照圖1、圖2的結構方案構建了氣缸套幾何誤差在線測量原型系統。圖5為直線度的評定結果，表3為分別利用ZEISS Calypso三坐標測量機和該原型系統對氣缸套同一母線進行測量所得到的測點坐標的對比。

在使用原型系統和三坐標測量機進行測量時，均以第1點為參照點，并設其坐標為（0，0），分別對同一氣缸套直線度、圓度及圓柱度誤差進行了評定，評定的結果如表4所示，可以看出兩者評定結果比較接近，最大偏差值在±0.005mm以內，證明了該原型系統的有效性。

表3 測點坐標對比 mm

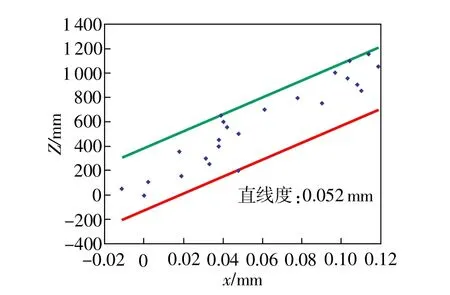
圖5 原型系統直線度評定結果

表4 三坐標測量機與原型系統誤差評定結果對比 mm

5 結束語

1）設計一種船用柴油機氣缸套幾何誤差在線測量系統，采用測量程序同步控制數控立車的運動及安裝在數控立車刀架上的激光位移傳感器的觸發采樣，通過融合傳感器的采樣值與數控立車的當前坐標計算出缸套表面各待測點的坐標。

2）分析在線測量系統的誤差來源，并建立了包含立車定位誤差、傳感器安裝誤差及傳感器測量誤差的綜合誤差模型。

3）建立基于非線性規劃方法的幾何誤差評定數學模型。通過與現有測量數據及誤差評定模型的對比分析，表明該模型的評定精度與現有誤差評定模型相比有一定的提高，且數學模型結構簡單、其幾何含義與國標提出的最小區域要求完全一致。

4）搭建在線測量原型系統并進行測量實驗，同時與三坐標測量機的測量結果進行對比，結果表明該原型系統測量準確度及誤差評定準確度較高。

[1]黎華文，鄭勝敏.柴油機氣缸套變形測量研究[J].裝備制造技術，2009（4）：13-15.

[2]Muralikrishnan B，Venkatachalam S，Raja J，et al.A note on the three-point method for roundness measurement[J].Precision Engineering，2005，29（2）：257-260.

[3]趙維謙，譚久彬，常承，等.超精圓度儀全自動誤差分離裝置的研制[J].儀器儀表學報，2000（2）：203-205.

[4]趙維謙，譚久彬，楊文國，等.基于兩步法超精密圓度儀誤差分離系統[J].中國機械工程，2000（11）：14-16.

[5]張振久，胡泓.基于激光跟蹤儀的轉臺系統幾何誤差檢測[J].中國激光，2012（11）：185-191.

[6]鄭宇，徐東明，張暉.大型圓柱件圓柱度誤差測量方法研究[J].長春理工大學學報：自然科學版，2013（6）：68-70.

[7]羅小燕，姜志宏，肖鋒，等.大型回轉類零件形位誤差測量系統的研究[J].機械設計與制造，2010（7）：108-109.

[8]Chou S，Sun C.Assessing cylindricity for oblique cylindrical features[J].International Journal of Machine Tools and Manufacture，2000，40（3）：327-341.

[9]陳偉琪.淺談數控加工中心的定位準確度檢測與補償[J].計量與測試技術，2011（6）：20-22.

[10]王寶仁，王婕，張承瑞，等.數控系統輪廓誤差矢量模型及其應用[J].計算機集成制造系統，2010（7）：1401-1407.

[11]鄭育軍，黃富貴.國內外形位誤差研究進展[J].工具技術，2006（11）：10-13.

[12]戴彧虹，劉新為.線性與非線性規劃算法與理論[J].運籌學學報，2014（1）：69-92.

[13]張嬌娜，郭偉偉，曹衍龍，等.圓柱度誤差評價方法研究[J].機床與液壓，2008（2）：106-109.

[14]田樹耀，黃富貴，田輝，等.一種基于Matlab的形位誤差評定方法[J].工具技術，2008（4）：95-97.

Research of a geometric error online measurement system for marine diesel engine cylinder liner

SU Shijie，DAI Yongjun，LI Qinfeng，TANG Wenxian
（College of Mechanical Engineering，Jiangsu University of Science and Technology，Zhenjiang 212003，China）

In the paper，a geometric error online measurement system for marine diesel cylinder liner has been designed.The impact of the position error and the installation and measurement errors of sensors on the accuracy of each measurement point coordinate was analyzed，and a mathematical model for measurement error was thus discussed.Accordingly，a mathematical model for evaluating the straightness，roundness，and cylindricity errors of diesel cylinder liners was established based on nonlinear programming.The model is more accurate compared with the existing measurement method.A prototype measurement system was constructed as well，and the experimental data show it is simple，precise and efficient.

marine diesel cylinder liner；geometric error；onlinemeasurement；nonlinear programming

A文章編號：1674-5124（2015）08-0022-05

10.11857/j.issn.1674-5124.2015.08.005

0 引言

船用柴油機氣缸套在加工時需嚴格保證幾何準確度，幾何誤差過大會導致裝配后出現密封性不佳、動力下降等不良后果[1]。國內企業在氣缸套加工過程中廣泛采用游標卡尺、卡規等進行檢測，存在著檢測準確度差、效率低等問題。在氣缸套加工完成后采用大型三坐標測量機進行終檢，雖然檢測準確度高，但存在著檢測周期及不合格零件返工周期長等缺點。

2014-11-12；

2015-01-19

江蘇省產學研聯合創新資金項目（BY2013066-05）

蘇世杰（1981-），男，副教授，主要從事復雜機電產品數字化設計與制造等研究。