星球車車輪的滑轉(zhuǎn)率估計方法

尤+波++時+洋

摘 要：未來的勘探任務(wù)要求星球車自主運行于復(fù)雜的星球表面，車輪滑轉(zhuǎn)率的有效估計是星球車高性能移動控制的關(guān)鍵，基于車輛地面力學(xué)理論，建立了基于滑轉(zhuǎn)率的車輪一土壤相互作用力學(xué)積分模型，推導(dǎo)了積分模型中集中力的解析表達(dá)式.針對模型方程組的高度耦合性和復(fù)雜非線性，分析了模型參數(shù)間的耦合關(guān)系；結(jié)合被動滑轉(zhuǎn)原理和參數(shù)關(guān)系分析結(jié)果，系統(tǒng)研究了星球車車輪的滑轉(zhuǎn)率估計方法.通過開展輪壤相互作用試驗，將車輪滑轉(zhuǎn)率的模型計算值與試驗所得值進(jìn)行比較，驗證了積分模型滑轉(zhuǎn)率估計方法的正確性，

關(guān)鍵詞：滑轉(zhuǎn)率；地面力學(xué)；被動滑轉(zhuǎn)；耦合關(guān)系

DOI： 10.15938/j.jhust.2015.02.005

中圖分類號：V476.4

文獻(xiàn)標(biāo)志碼：A

文章編號：1007-2683（2015）02-0023-05

0 引 言

同探索海洋、陸地和近地空間一樣，人類對外部星球的探索本身就是對地球生命進(jìn)化研究的重要一步.星球表而環(huán)境的復(fù)雜性與不確定性，使星球車在運行過程中極易發(fā)生滑轉(zhuǎn)現(xiàn)象，對星球車移動系統(tǒng)方面研究提出了許多挑戰(zhàn).滑轉(zhuǎn)率估計方法研究可以使人們更好了解車輪滑轉(zhuǎn)狀態(tài)，對星球車控制策略設(shè)計、路徑規(guī)劃研究以及驅(qū)動力驅(qū)動力學(xué)特性分析具有重要意義.

文提出利用根據(jù)星球車車轍痕跡檢測車輪滑轉(zhuǎn)率的方法，但該方法中車輪痕跡必須人工測量，無法實現(xiàn)自動檢測；文通過視覺方法檢測車轍的形狀，經(jīng)過數(shù)據(jù)轉(zhuǎn)換實現(xiàn)滑轉(zhuǎn)率的檢測，但對于無輪刺的星球探測車車輪，該方法并不適用；應(yīng)用地面力學(xué)解決星球車運動控制問題一直是該領(lǐng)域研究的熱點與難點，文在忽略離去角的基礎(chǔ)上，基于Wong-Reece的正應(yīng)力分布模型和Janosi的塑性剪切特性模型推導(dǎo)了車輪集中力的封閉解析表達(dá)式，但對于星球車車輪滑轉(zhuǎn)率的估計方法系統(tǒng)研究很少.

本文基于地面力學(xué)理論，建立車輪在被動滑轉(zhuǎn)狀態(tài)下的車輪一土壤相互作用力學(xué)積分模型，推導(dǎo)車輪掛鉤牽引力和支持力的解析表達(dá)式，在分析模型參數(shù)耦合關(guān)系的基礎(chǔ)上，提出星球車車輪滑轉(zhuǎn)率估計方法，最后結(jié)合試驗數(shù)據(jù)驗證該方法的正確性.

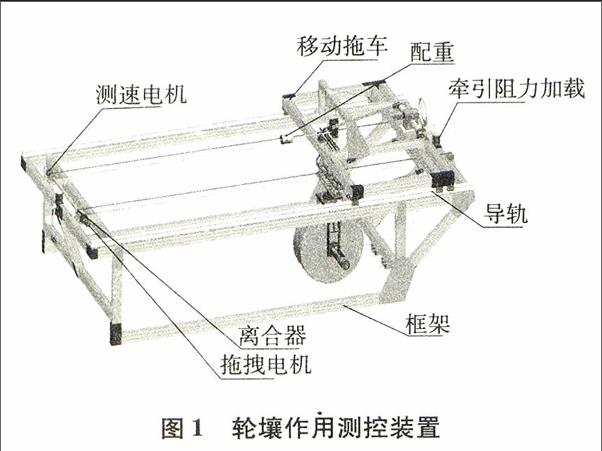
1 輪壤相互作用測控裝置

車輪與土壤相互作用測控裝置如圖1所示，該裝置包括前進(jìn)電機(jī)、拖拽電機(jī)和轉(zhuǎn)向電機(jī)3個伺服電機(jī)，具有離合器、配重、輪壓加載機(jī)構(gòu)、牽引阻力加載機(jī)構(gòu)以及導(dǎo)軌等機(jī)械裝置，安裝了六維力/力矩傳感器以及測速電機(jī)等感知器件.

在離合器斷開的情況下，單獨驅(qū)動車輪前進(jìn)電機(jī)帶動移動拖車在導(dǎo)軌上運動，可以開展車輪被動滑轉(zhuǎn)試驗.基于配重和輪壓加載機(jī)構(gòu)，可以設(shè)定穩(wěn)定的車輪正壓力；通過牽引阻力加載，可以設(shè)定恒定的車輪掛鉤牽引阻力，車輪正壓力和掛鉤牽引阻力由六維力/力矩傳感器進(jìn)行測量，移動拖車的速度由測速電機(jī)轉(zhuǎn)換獲得，車輪滑轉(zhuǎn)率通過拖車速度和車輪滾動角速度轉(zhuǎn)換得到.圖2為測試車輪模型.

2 基于滑轉(zhuǎn)率的星球車輪壤相互作用建模

2.1滑轉(zhuǎn)率定義

滑轉(zhuǎn)率反映了車輪實際前進(jìn)線速度和滾動速度之間的偏差程度，用式（1）進(jìn)行定義：式中：r為車輪半徑；ω為車輪滾動角速度；v為車輪前進(jìn)線速度.

在該定義中，滑轉(zhuǎn)率s的范圍為[-1，l].當(dāng)車輪滾動速度大于實際前進(jìn)速度，車輪處于滑轉(zhuǎn)狀態(tài)，此時s>0；當(dāng)車輪滾動速度等于實際前進(jìn)速度，車輪處于純滾動狀態(tài)，此時s=0；當(dāng)車輪滾動速度小于實際前進(jìn)速度，車輪處于滑移狀態(tài)，此時s<0；在普遍情況下，平地運動或爬坡時，車輪滑轉(zhuǎn)率s≥0；車輪下坡時，滑轉(zhuǎn)率s<0.

2.2輪壤相互作用力學(xué)模型

當(dāng)車輪處于被動滑轉(zhuǎn)狀態(tài)時，輪壤相互作用力學(xué)模型如圖3所示，星球車車輪在星球表面運動類似于車輪與松軟地面相互作用的情形.圖3中：ω為星球車車輪轉(zhuǎn)動角速度；T為車輪轉(zhuǎn)動力矩；?DP為掛鉤牽引阻力；形為車輪正壓力；υ為車輪實際前進(jìn)線速度；r為車輪半徑；從車輪豎直位置到接人土壤位置所對應(yīng)的輪心角為接近角角θ1；從車輪豎直位置到離開土壤位置所對應(yīng)輪心角為離去角θ2∶σ（θ）為車輪徑向應(yīng)力分布函數(shù)；τ（θ）為車輪剪切應(yīng)力分布函數(shù)；θM為車輪最大徑向應(yīng)力所對應(yīng)的輪心角，松軟土壤對驅(qū)動車輪的作用力可以表現(xiàn)為連續(xù)的應(yīng)力形式，即徑向應(yīng)力σ（θ）和剪切應(yīng)力τ（θ），應(yīng)力在車輪上的連續(xù)作用平衡于掛鉤牽引阻力和車輪壓力，

基于Wong-Reece的研究成果[16]，可以得到車輪徑向應(yīng)力分布函數(shù)：式中：κc為土壤粘聚模量，κ為土壤摩擦模量，n為變形指數(shù)，6為車輪寬度，C1和c2為土壤最大應(yīng)力角系數(shù)，c3為土壤離去角系數(shù)，結(jié)合Janosi的塑性剪切特性模型[17]和式（l）可以得到車輪剪切應(yīng)力分布函數(shù)：式中∶c為土壤內(nèi)聚力；γ為土壤內(nèi)摩擦角；j（θ）為驅(qū)動車輪剪切位移；jo為剪切應(yīng)力一位移曲線模量.

當(dāng)車輪處于穩(wěn)定狀態(tài)時，掛鉤牽引力F〈sub〉DP〈/sub〉、法向支持力Fn與車輪受到的掛鉤牽引力阻力fDP、車輪正壓力W相互平衡，對車輪徑向應(yīng)力和剪切應(yīng)力進(jìn)行積分，可以得到式（7）.

3 滑轉(zhuǎn)率估計方法研究

3.1 輪壤作用模型參數(shù)關(guān)系分析

基于以上對輪壤相互作用模型的分析，式（7）是非線性與高度耦合的積分方程組，掛鉤牽引力和法向支持力是關(guān)于滑轉(zhuǎn)率、輪壤作用接觸角、車輪參數(shù)及土壤參數(shù)的函數(shù)，輪壤相互作用模型參數(shù)關(guān)系如圖4所示，徑向應(yīng)力分布函數(shù)σ（θ）描述了在輪壤接觸范圍內(nèi)驅(qū)動輪受到沿半徑方向的應(yīng)力分布，體現(xiàn)了土壤的承壓特性[18]，由土壤粘聚模量κ、摩擦模量k。、變形指數(shù)n、車輪半徑r、車輪寬度6和接觸角θ1、θ2、θm所決定，θ2是關(guān)于最大離去角系數(shù)c3，與θ1的函數(shù)，θM是關(guān)于最大應(yīng)力角系數(shù)c1、c2、θ1與滑轉(zhuǎn)率s的函數(shù).剪切應(yīng)力分布函數(shù)τ（θ）描述了土壤對驅(qū)動輪沿切向的應(yīng)力分布，體現(xiàn)了土壤的剪切特性[19]，由內(nèi)聚力c、土壤內(nèi)摩擦角γ、徑向應(yīng)力函數(shù)σ（θ）、車輪剪切位移j（θ）和剪切應(yīng)力一位移曲線模量j0決定，j（θ）是關(guān)于車輪半徑r、接觸角θ1，以及滑轉(zhuǎn)率s的函數(shù).

車輪的正壓力W決定了土壤對車輪的徑向應(yīng)力，同時剪切應(yīng)力的在垂直方向上的分量對車輪有一定支撐作用.掛鉤牽引力阻力fDP決定了車輪受到的剪切應(yīng)力，并且徑向應(yīng)力的水平分量對車輪也有一定牽引作用.

3.2估計方法研究

通過輪壤相互作用模型參數(shù)關(guān)系解析，在車輪參數(shù)、土壤參數(shù)已知以及車輪正壓力、掛鉤牽引力阻力恒定的情況下，車輪被動滑轉(zhuǎn)時基于式（7）”r以求解滑轉(zhuǎn)率s和接觸角θ1、θ2，具體求解流程如圖5所示.當(dāng)不考慮土壤回彈部分對車輪的影響時，離去角θ2，忽略為0，即離去角系數(shù)c3為0；當(dāng)考慮土壤回彈部分對車輪的影響時，通常采用經(jīng)驗公式θ2=-0.125θ1，，離去角系數(shù)c3為-0.125，本文中對滑轉(zhuǎn)率進(jìn)行估計采用后者.因此，在車輪穩(wěn)定運行狀態(tài)下，利用式（7）可以求解滑轉(zhuǎn)率s和接近角θ1.由于該方程組無解析解，需要經(jīng)過多次迭代來求得方程組解，因此利用Matlab編寫程序，采用fsolve函數(shù)進(jìn)行求解.

針對驅(qū)動輪性能參數(shù)進(jìn)行求解方式，基于被動滑轉(zhuǎn)原理和基于主動滑轉(zhuǎn)原理在已知參數(shù)和求解參數(shù)上有較大不同，基于被動滑轉(zhuǎn)原理求解是將掛鉤牽引力阻力fDP和車輪正壓力W作為已知參數(shù)，利用方程組求解滑轉(zhuǎn)率s和接近角θ1；基于主動滑轉(zhuǎn)原理求解是將滑轉(zhuǎn)率s和車輪正壓力W作為已知條件，結(jié)合方程對車輪發(fā)生沉陷時的接近角θ1進(jìn)行求解.相較于基于主動滑轉(zhuǎn)原理對車輪性能參數(shù)進(jìn)行求解的方式，基于被動滑轉(zhuǎn)原理的求解更加復(fù)雜，但星球車在運行過程中滑轉(zhuǎn)率往往處于未知狀態(tài)，因此該方法更加貼近實際運行狀態(tài)，求解出的滑轉(zhuǎn)率在星球車控制應(yīng)用中具有重要意義.

4 試驗驗證及結(jié)果分析

試驗采用松軟干沙模擬星球土壤，通過設(shè)置穩(wěn)定的掛鉤牽引力和車輪輪壓進(jìn)行車輪被動滑轉(zhuǎn)試驗.干沙力學(xué)參數(shù)如表l所示.

通過車輪一土壤相互作用試驗，測得車輪穩(wěn)定運行時的數(shù)據(jù)作為試驗結(jié)果，針對同樣的掛鉤牽引力和車輪輪壓的試驗重復(fù)3次，并求取平均值作為最終試驗數(shù)據(jù)，以確保試驗數(shù)據(jù)的準(zhǔn)確性，

被測輪半徑400mm，寬度125mm，通過對車輪一土壤相互作用試驗數(shù)據(jù)統(tǒng)計，可以得到在掛鉤牽引阻力分別為40N、60N和80N下滑轉(zhuǎn)率隨車輪壓力變化的曲線，如圖6所示.

從試驗結(jié)果可以看出，當(dāng)掛鉤牽引阻力一定時，無論是通過模型計算的滑轉(zhuǎn)率還是經(jīng)過試驗得到的滑轉(zhuǎn)率都隨著車輪壓力增大而減小，并且減小的速度逐漸變緩；在一定車輪壓力下，車輪掛鉤牽引阻力越小，引起的滑轉(zhuǎn)率越小，

圖6（a）中試驗滑轉(zhuǎn)率與理論滑轉(zhuǎn)率兩者之間卡H對誤差為0.6%-8%；圖6（b）中兩者之間相對誤差為1%-9.2%；圖6（c）中兩者之間相對誤差為1.3%-9.6%.以上結(jié)果表明滑轉(zhuǎn)率的相對誤差能夠維持在10%以下，驗證了積分模型和滑轉(zhuǎn)率估計方法的合理性與正確性.

4 結(jié) 論

在地面力學(xué)和被動滑轉(zhuǎn)原理研究的基礎(chǔ)上，建立了星球車車輪一土壤相互作用力學(xué)積分模型，推導(dǎo)了基于滑轉(zhuǎn)率的車輪掛鉤牽引力和支持力的解析表達(dá)式.基于對模型參數(shù)之間耦合關(guān)系的分析，系統(tǒng)研究了車輪滑轉(zhuǎn)率的估計方法.結(jié)合輪壤相互作用試驗及試驗數(shù)據(jù)，通過比較模型計算的滑轉(zhuǎn)率和車輪實際的滑轉(zhuǎn)率，驗證了積分模型和滑轉(zhuǎn)率估計方法的合理性與正確性.