一種降低MIMO-OFDM系統PAPR的半盲SLM方法

紀金偉,任光亮,張會寧

(西安電子科技大學綜合業務網理論及關鍵技術國家重點實驗室,陜西西安 710071)

一種降低MIMO-OFDM系統PAPR的半盲SLM方法

紀金偉,任光亮,張會寧

(西安電子科技大學綜合業務網理論及關鍵技術國家重點實驗室,陜西西安 710071)

提出了一種降低Alamouti編碼的多輸入多輸出正交頻分復用系統峰均比的半盲選擇映射方法.為在發送端降低復雜度以及把邊信息嵌入到發送數據中,該方法把輸入正交頻分復用符號序列分割成交織的子塊,并對每一子塊利用轉換向量生成時域備選信號,然后把每一子塊對應的備選信號乘以不同的相位旋轉因子后相加生成發送備選信號.在接收端,通過聯合檢測每一子塊對應的相位旋轉因子得到邊信息,從而在不傳輸邊信息的情況下檢測出發送數據.分析與仿真結果表明,與已有的半盲選擇映射方法相比,文中方法可以達到更好的邊信息檢測性能以及相近的降峰均比與誤比特率性能,并且收發端的復雜度大大降低.

多輸入多輸出正交頻分復用;峰均比;選擇映射;邊信息

多輸入多輸出正交頻分復用(Multiple-Input Multiple-Output Orthogonal Frequency Division Multiplexing,MIMO-OFDM)技術具有可以提供高速數據傳輸以及空間分集與復用增益等優點,因此,在無線通信系統中得到了廣泛應用[1].然而,與正交頻分復用(Orthogonal Frequency Division Multiplexing, OFDM)系統相同,MIMO-OFDM系統同樣存在著發送信號峰均比(Peak to Average Power Ratio,PAPR)過高的問題.高PAPR的信號在經過功放等非線性器件時會產生嚴重的帶內失真與帶外輻射,造成系統誤比特率(Bit Error Rate,BER)性能下降以及對臨近信道的干擾[2].

針對降低MIMO-OFDM系統PAPR的問題,文獻中提出了很多種方法[1,3-8].在這些方法中,選擇映射(Se Lected Mapping,SLM)是一種線性、高性能的降PAPR方法.但是為在接收端檢測出發送數據,常規的SLM方法需要傳輸代表發射端選擇的相位旋轉矢量序號的邊信息,這降低了系統的數據速率,且使系統更加復雜以及增加了傳輸時延.文獻[7]利用Alamouti空頻分組碼(Space-Frequency Block Codes,SFBC)固有的冗余性,提出了一種不需傳輸邊信息的SLM方法.該方法相位旋轉矢量的元素只能取1或-1,這在很多場景下是應用受限或者不適用的.文獻[8]通過對相位旋轉矢量的一些元素進行擴展以及檢測不同相位旋轉矢量對應元素之間能量的差異性,實現了Alamouti SFBC系統中邊信息的檢測.該方法由于增強了一些子載波上數據的傳輸功率而導致了潛在的BER性能損失,并且性能損失隨著調制階數變高以及相位旋轉矢量個數的增加而變大.文獻[1]針對Alamouti SFBC系統提出了一種相位偏移半盲SLM方法,在接收端通過檢測與每個相位旋轉矢量對應的相位旋轉因子得到邊信息,其BER性能稍優于文獻[7].以上這些SLM方法雖然不需要傳輸邊信息,但是發射端的復雜度非常高.此外,文獻[1,7]在接收端均利用最大似然的方法進行邊信息檢測,從而導致接收端復雜度很高.

針對現有Alamouti MIMO-OFDM系統中半盲SLM方法收發端復雜度過高的問題,筆者提出了一種新的半盲SLM方法.在發送端,該方法把輸入OFDM符號塊分割成交織的子塊,并對每一子塊利用轉換向量生成時域備選信號,然后把每一子塊對應的備選信號乘以不同的相位旋轉因子后,相加生成發送備選信號,實現了低復雜度備選信號的生成以及邊信息的嵌入.在接收端,通過聯合檢測每一子塊對應的相位旋轉因子得到邊信息,從而在不傳輸邊信息的情況下檢測出發送數據.與已有的半盲SLM方法相比,文中方法可以達到更好的邊信息檢測性能以及相近的降PAPR性能與BER性能,并且收發端的復雜度大大降低.

1 系統模型

考慮采用Alamouti SFBC的兩天線MIMO-OFDM系統,假設輸入OFDM符號序列X=[X(0), X(1),…,X(N-1)]T,則兩根天線上的發送數據向量分別為

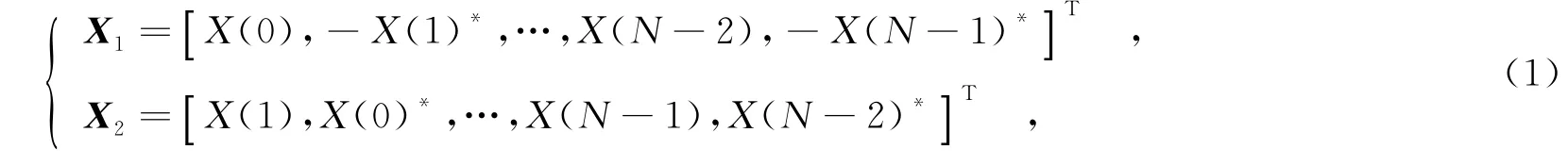
其中,N為系統子載波個數,(·)*表示求共軛運算.經過快速傅里葉逆變換(Inverse Fast Fourier Transform,IFFT)后,得到發送的時域信號向量xi=[xi(0),xi(1),…,xi(LN-1)]T為

其中,i=1,2;n=0,1,…,LN-1,L為過采樣因子.每一根天線上發送信號的PAPR定義為

則Alamouti MIMO-OFDM系統發送信號的PAPR定義為

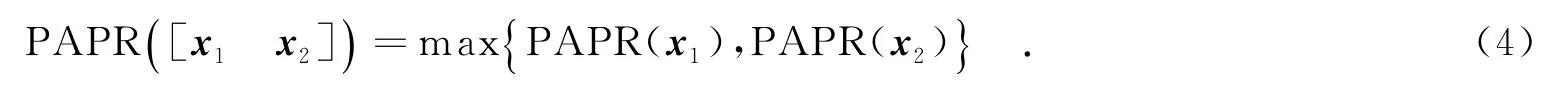
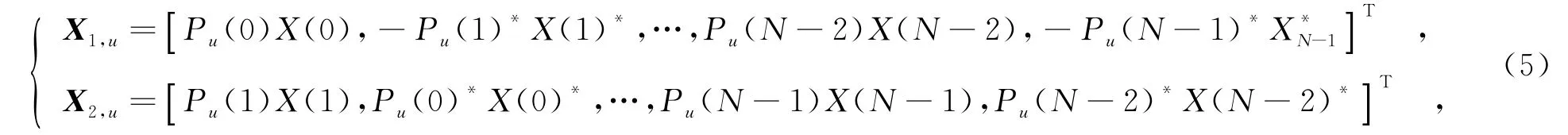
在傳統SLM方法中,將X與U個相位旋轉矢量Pu=[Pu(0),Pu(1),…,Pu(N-1)]T,0≤u≤U-1分別相乘,得到U個輸入備選符號序列Xu=[Pu(0)X(0),Pu(1)X(1),…,Pu(N-1)X(N-1)]T,其中Pu(k)=exp(jθu(k)),θu(k)∈(-π,π].經過Alamouti SFBC編碼,映射到兩根天線上的備選符號序列X1,u和X2,u分別為則第1根天線上對應的相位旋轉矢量P1,u=[Pu(0),(Pu(1))*,…,Pu(N-2),(Pu(N-1))*]T,第2根天線上的相位旋轉矢量P2,u=[Pu(1),(Pu(0))*,…,Pu(N-1),(Pu(N-2))*]T.分別對兩天線上的備選符號序列進行IFFT操作,得到時域備選信號對x1,u,x2,u.從x1,u與x2,u中選擇PAPR最小的信號對作為發射信號,則發射信號為

2 低收發復雜度的半盲SLM方法

2.1 時域信號的性質

本節介紹采用Alamouti SFBC的兩天線MIMO-OFDM系統時域信號的兩個性質,文中方法利用這兩個性質大大降低了發射端的復雜度.

性質1假設天線上的輸入OFDM符號序列Xi=[Xi(0),Xi(1),…,Xi(N-1)]T,相位旋轉矢量Pi,u=[Pi,u(0),Pi,u(1),…,Pi,u(N-1)]T,頻域備選OFDM符號序列Xi,u=[Pi,u(0)Xi(0),Pi,u(1)Xi(1),…,Pi,u(N-1)Xi(N-1)]T,則時域備選信號xi,u=IFFTLN(Xi,u)=pi,u?LNxi,其中xi=IFFTLN(Xi), pi,u=IFFTLN(Pi,u),為生成備選信號的轉換向量.

這一性質由數字信號的循環卷積性質容易得證.文獻[2,9]利用這一性質,通過巧妙設計轉換向量,并用時域循環卷積代替IFFT運算,大大降低了OFDM系統中產生備選信號的復雜度.

若天線上的備選OFDM符號序列Xi,u被分為M個交織子塊,1≤m≤M,其中,M=2q,q為非零自然數,每一子塊上采用的相位旋轉矢量都與一轉換向量相對應,即則對每一子塊進行LN/M點IFFT運算得到的時域信號可寫為

性質2若天線上的輸入OFDM符號序列Xi偶數子載波上的符號序列=[Xi(0),0,…, Xi(N-2),0]T,奇數子載波上的符號序列則對與分別進行LN點IFFT運算產生的時域信號與的前LN/2個采樣點向量分別為與其中WLN=ex p(j2π(LN)),☉表示元素乘運算;并且與可分別由與經過時域循環擴展與反循環擴展得到,即

2.2 文中SLM方法的發射機

筆者基于以上性質提出了新的半盲SLM方法,其發射機結構如圖1所示.輸入OFDM符號序列X經過Alamouti SFBC編碼后,首先,將第1根天線上的輸入OFDM符號序列X1分割成M個交織的子塊,其中,M=2q,q為非零自然數.然后,對X1的M個子塊進行處理,生成備選信號,并將邊信息嵌入到發送數據中.最后,利用兩根天線上發送信號之間的相關性,通過第1根天線上的時域備選信號產生第2根天線上的備選信號,并從兩天線上的備選信號對中選擇PAPR最低的信號對作為發射信號.文中方法通過將X1分為M個子塊,增加了文獻中轉換向量的個數,并且實現了邊信息的嵌入;通過巧妙設計發射機結構,使得發射端計算復雜度遠低于已有方法.發射端具體的處理步驟如下:

步驟1 將輸入OFDM符號序列進行Alamouti SFBC編碼,并將第一根天線上的頻域發送符號序列X1分割成M個交織的子塊,1≤m≤M.

圖1 文中SLM方法的發射機結構示意圖

雙正交向量組是一組元素取值只為0和1的向量組,假設向量組的歸一化最小漢明距離為dmin/M,對于長度等于M的U個雙正交向量,若M=U/2,雙正交向量組可使dmin/M=1/2.因此,把輸入OFDM符號序列交織分割為M個子塊,其中為向上取整運算).由雙正交向量的性質,將每個轉換向量當作一個整體,利用兩個轉換向量就可以構造出至少M/2個子塊上采用不同轉換向量的U個轉換向量組;進一步,把R個轉換向量每兩個一組分為Q組,每組利用雙正交向量性質構造T個漢明距離最大的轉換向量組,使得QT≥U,這樣可保證構造的U個相位旋轉矢量Pu之間的差別,以保證降PAPR性能.

其中,0≤v≤N/2-1,mo為奇數,且分別為X的第mo與mo+1個交織子塊)與分別為使發送信號PAPR最小的相位旋轉因子與相位旋轉矢量.

2.3 數據檢測

在接收端,去掉循環前綴后,得到的接收信號y= [y(0),y(1),…,y(LN-1)]T為

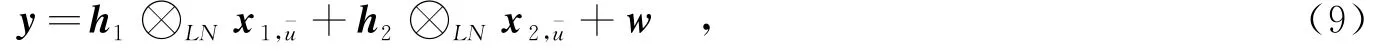
其中,?LN為LN點的循環卷積運算;為第i根天線到接收端的時域信道沖擊響應,L為信道沖擊響應的有效長度;w= [w(0),w(1),…,w(LN-1)]T,為加性高斯白噪聲.對y進行快速傅里葉變換操作,得到第k個子載波上的接收數據為

其中,Hi(k)為hi在第k個子載波上的信道頻域響應,W(k)為第k個子載波上的加性高斯白噪聲.假設信道頻域沖擊響應在連續兩個子載波上相同,即Hi(2v)=Hi(2v+1).將式(8)帶入式(10),并令Z(2v)=得

由式(11),可得

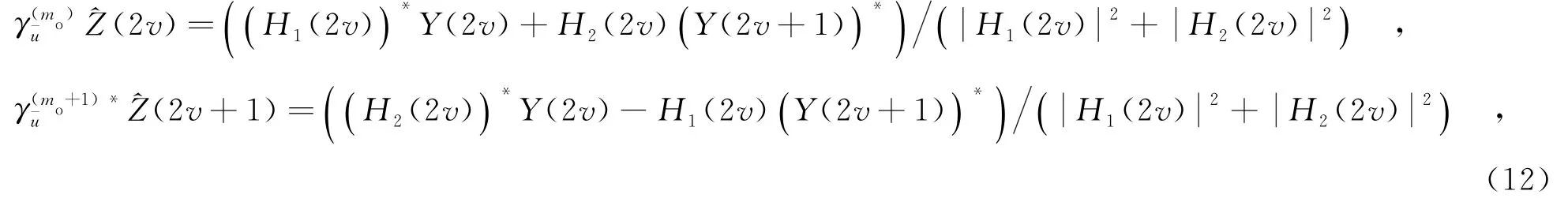
假設調制符號的星座圖為Q Q,由于采用的相位旋轉矢量使得備選輸入OFDM符號序列的每個符號仍然在原星座圖Q Q上,即Z(2v)∈Q Q,Z(2v+1)∈Q Q,對于第mo個子塊,相位旋轉因子可估計為

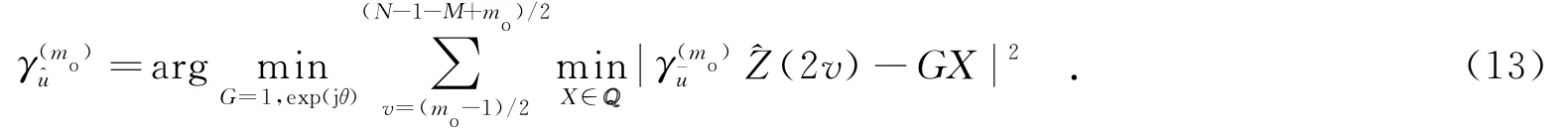
對于第mo+1個子塊,相位旋轉因子可估計為

其中,d(a,b)為向量a與向量b之間的漢明距離.得到邊信息的估計后就能得到發射端采用的相位旋轉矢量的估計值從而從接收數據中恢復出發送數據.

為使接收端檢測性能最好,不同的相位向量γu與γv,u≠v之間的漢明距離應最大.由于雙正交向量組可以保證向量之間的最小漢明距離 可利用雙正交向量組構造γu.將γu與U個雙正交向量一一對應,并將向量中的0和1分別替換為1和exp(jθ),即構造出U個相位向量.此外,為使檢測性能最好,應選擇θ的值使得經過相位旋轉之后的星座點與原星座點之間的差別最大.對奇數的m,θ可取為

對偶數的m,θ可取為

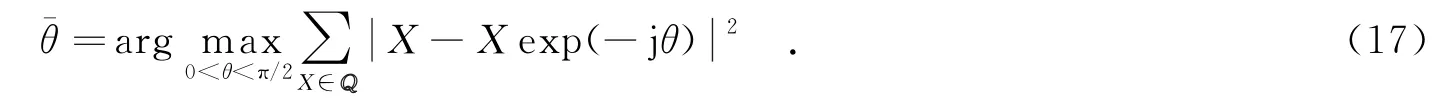
顯然對于同一個星座圖,式(16)與式(17)的解相同.對于正交相移鍵控(Quadrature Phase Shift Keying, QPSK)、16正交振幅調制(Quadrature Amplitude Modulation,QAM)與64-QAM,文獻[10]中給出了式(16)的解,即因此,文中取

2.4 復雜度分析

文中以收發每個OFDM符號需要的復數乘與復數加的次數計算收發端的復雜度,并將文中方法與文獻[1]半盲SLM方法的復雜度進行對比.在發送端,文中方法首先對M個交織子塊分別進行LN/M點的IFFT運算,需要(LN/2)lb(LN/M)次復數乘法與LN lb(LN/M)次復數加法;由文獻[9]中轉換向量的性質可知,利用轉換向量產生每一子塊的備選信號最多需要3LN/M次復數加法,則產生U個備選信號的M個子塊的備選信號最多需要3ULN次復數加法;將邊信息嵌入發送數據符號中,U個備選信號需要ULN次復數乘運算;U個備選信號的I=lb M-1級蝶形運算,需要UILN/2次復數乘法運算與UILN次復數加法運算;U個備選信號的與W進行元素乘運算,需要ULN/2次復數乘運算;將與相加得到第1根天線上的備選信號需要ULN次復數加運算.此外,由與分別產生與并將與相加需要ULN次復數乘與ULN次復數加運算.因此,文中方法需要的復數乘運算量的次數為

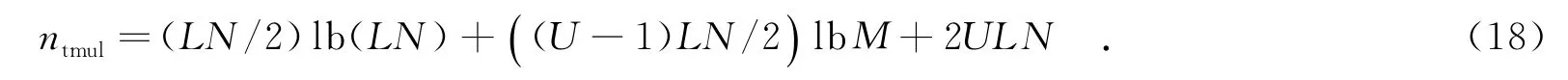
最多需要的復數加運算量的次數為

而文獻[1]中發射端需要的運算為兩根天線上的U個LN點IFFT運算以及將邊信息嵌入發送數據符號的運算,因此,復數乘與復數加的次數分別為

在接收端,文中方法需要首先對接收頻域符號進行Alamouti SFBC解碼,然后對每一子塊計算式(13)或式(14),因此,檢測邊信息需要的復數乘與復數加的次數分別為

其中,q為調制星座圖Q Q的階數.而文獻[1]中邊信息檢測需要的復數乘與復數加的次數分別為

定義復雜度減少率(Computational Complexity Reduction Ratio,CCRR)為

其中,C與C0分別為文中算法與對比算法的運算量.表1給出了LN=512,1 024與2 048時,文中方法相對于文獻[1]方法發射端復數乘運算量的CCRR值.

表1 文中方法相比于文獻[1]方法發射端復數乘運算量的CCRR

3 仿真結果

為了驗證文中方法的有效性,對其性能進行計算機仿真并與文獻[1]中的方法進行對比.仿真系統子載波個數N=256,調制方式為16-QAM調制,信道模型采用文獻[7]中的多徑衰落信道.為仿真PAPR性能,過采樣因子取L=4.仿真假設收發端完全同步并且在接收端已知信道信息.

圖2給出了文中方法與文獻[1]以及文獻[6]方法的降PAPR性能對比圖,其中PAPR以累積分布函數(Complementary Cumulative Distribution Function,CCDF)度量.從圖2可以看出,與文獻[1]不需傳輸邊信息的半盲SLM方法相比,文中方法的降PAPR性能略有下降,但是文中方法的收發端復雜度大大降低;與文獻[6]需要傳輸邊信息的低復雜度SLM方法相比,文中方法的降PAPR性能好很多,例如在U=4,8, 16,Pr[PAPR≥PAPR0]=10-3時,相比文獻[6]方法,文中方法的降PAPR性能增益分別為0.8dB,0.7dB與0.6 d B,并且文中方法不需要傳輸邊信息.

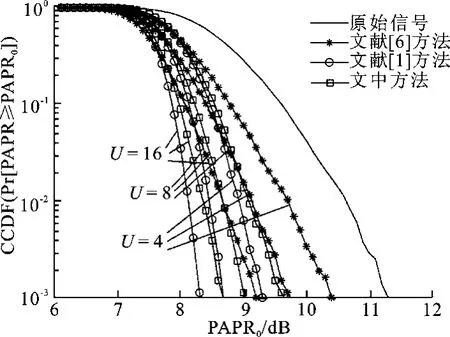
圖2 文中方法與文獻[1,6]方法的降PAPPR性能對比圖

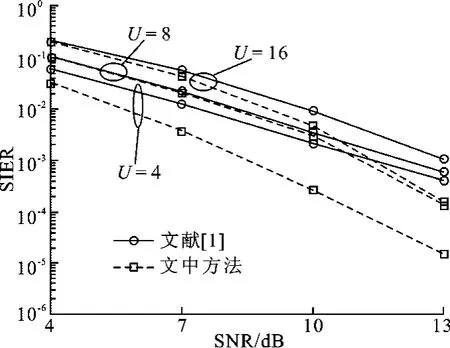
圖3 文中方法與文獻[1]方法的SIER性能對比圖

圖3給出了文中方法與文獻[1]方法的誤邊信息檢測率(SIER)性能對比圖.從圖3可以看出,SIER性能隨著備選信號數目U的增大而變差,這是因為文中方法為保證相位矢量之間的最小漢明距離,隨著U的增大,輸入OFDM符號分塊數目M增大,導致每一子塊的子載波個數減少,檢測性能變差;而對于文獻[1]方法,隨著U的增大,攜帶邊信息的相位因子分辨率變小,導致檢測性能變差.另一方面,對于固定的U,文中方法的SIER性能優于文獻[1]的方法,并且邊信息檢測復雜度也大大降低.

圖4給出了文中方法與文獻[1]方法以及普通SLM方法的BER性能對比圖,其中在普通SLM方法中假設接收端邊信息已知.從圖4可以看出,文中方法與文獻[1]方法可以達到一致的BER性能.對于U=4,兩者均可以達到與具有完美邊信息的普通SLM相近的BER性能,這是由于在給定的信道與SNR條件下,文中方法與文獻[1]方法的SIER均遠小于系統的BER.隨著U的增大,SIER性能變差,從而BER性能變差.當U=16時,在低信噪比時(小于7 d B),兩者的BER性能均比具有完美邊信息的普通SLM略差;隨著SNR的增加,SIER性能變好,兩者均可以達到與具有完美邊信息的普通SLM相近的BER性能.

圖4 文中方法與文獻[1]方法以及普通SLM方法的BER對比圖

4 結束語

針對現有降低Alamouti MIMO-OFDM系統PAPR的SLM方法需要傳輸邊信息及復雜度過高的問題,筆者提出了一種新的不需傳輸邊信息的低收發復雜度的半盲SLM方法.該方法通過巧妙設計發射機結構,實現了發射端的低復雜度以及邊信息的嵌入,并且給出了接收端低復雜度的邊信息檢測方案.與現有文獻方法相比,文中方法收發端的復雜度大大降低,并且可以達到更好的SIER性能與相近的BER與降PAPR性能.由于良好的性能與很低的收發復雜度,該方法對于實際系統具有很大的工程價值與實用意義.

[1]Jiang T,Ni C X,Guan L L.A Novel Phase Offset SLM Scheme for PAPR Reduction in Alamouti MIMO-OFDM Systems without Side Information[J].IEEE Signal Processing Letters,2013,20(4):383-386.

[2]Ji J W,Ren G L.A New Modified SLM Scheme for Wireless OFDM Systems without Side Information[J].IEEE Signal Processing Letters,2013,20(11):1090-1093.

[3]王金祥,吳新春,毛志剛,等.降低OFDM信號PAPR的低復雜度PTS方法[J].西安電子科技大學學報,2010,37 (2):326-333. Wang Jinxiang,Wu Xinchun,Mao Zhigang,et al.Low Complexity PTS Scheme for PAPR Reduction of OFDM Signals [J].Journal of Xidian University,2010,37(2):326-333.

[4]Kwon U K,Dongsik K,Im G H.Amplitude Clipping and Iterative Reconstruction of MIMO-OFDM Signals with Optimum Equalization[J].IEEE Transactions on Wireless Communications,2009,8(1):268-277.

[5]Latinovic Z,Bar-Ness Y.SFBC MIMO-OFDM Peak-to-average Power Ratio Reduction by Polyphase Interleaving and Inversion[J].IEEE Communications Letters,2006,10(4):266-268.

[6]Wang S H,Li C P.A Low-complexity PAPR Reduction Scheme for SFBC MIMO-OFDM Systems[J].IEEE Signal Processing Letters,2009,16(11):941-944.

[7]Naeiny M F,Marvasti F.Selected Mapping Algorithm for PAPR Reduction of Space-frequency Coded OFDM Systems without Side Information[J].IEEE Transactions on Vehicular Technology,2011,60(3):1211-1216.

[8]Hu W W,Ciou Y C,Li C P,et al.PAPR Reduction Scheme in SFBC MIMO-OFDM Systems without Side Information [C]//Proceedings of IEEE International Conference on Communications.Piscataway:IEEE,2013:4708-4712.

[9]Wang C L,Ku S J.Novel Conversion Matrices for Simplifying the IFFT Computation of an SLM-based PAPR Reduction Scheme for OFDM Systems[J].IEEE Transactions on Communications,2009,57(7):1903-1907.

[10]Joo H S,Heo S J,Jeon H B,et al.A New Blind SLM Scheme with Low Decoding Complexity for OFDM Systems[J]. IEEE Transactions on Broadcasting,2012,58(4):669-676.

(編輯:李恩科)

Semi-blind SLM scheme for reducing the PAPR of MIMO-OFDM systems

JI Jinwei,REN Guangliang,ZHANG Huining
(State Key Lab.of Integrated Service Networks,Xidian Univ.,Xi’an 710071,China)

A semi-blind selected mapping(SLM)scheme is addressed to reduce the peak-average-power ratio(PAPR)of Alamouti coded multiple-input multiple-output orthogonal frequency division multiplexing (MIMO-OFDM)systems.To enable low computational complexity as well as embedding of the side information into the data symbols at the transmitter,the input OFDM symbol sequence is partitioned into several interleaved subblocks,each of which is transformed into time-domain candidate signals by using the conversion vectors,and then the candidate signals for each subblock are multiplied with different phase offset factors and added up to obtain the transmitted candidate signals.At the receiver,the side information can be obtained by jointly detecting the phase offset factors of each subblock and the transmitted data can be detected without transmitting the side information.Analysis and simulation show that the proposed scheme can achieve a better side information detection performance and almost the same PAPR reduction and bit error rate(BER)performance with a much lower complexity at both the transmitter and receiver,as compared to the available semi-blind SLM schemes.

multiple-input multiple-output orthogonal frequency division multiplexing(MIMO-OFDM); peak-to-average power ratio(PAPR);selected mapping(SLM);side information

TN911.7

A

1001-2400(2015)05-0013-07

2014-09-05< class="emphasis_bold">網絡出版時間:

時間:2014-12-23

國家重點基礎研究計劃(973計劃)資助項目(2014CB340205);測控通信創新探索基金資助項目(201409B)

紀金偉(1986-),男,西安電子科技大學博士研究生,E-mail:jjw86215@163.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20141223.0946.003.html

10.3969/j.issn.1001-2400.2015.05.003