并行矩量法分析波導縫隙天線的輻射特性

王 永,林中朝,張 玉,梁昌洪

(西安電子科技大學天線與微波技術重點實驗室,陜西西安 710071)

并行矩量法分析波導縫隙天線的輻射特性

王 永,林中朝,張 玉,梁昌洪

(西安電子科技大學天線與微波技術重點實驗室,陜西西安 710071)

采用并行矩量法對工程中遇到的Ka波段波導縫隙天線進行仿真計算.矩量法中難以實現端口匹配,導致其難以有效地處理行波天線問題.為了有效地解決這一難題,采用等效原理和模式匹配法在端口面上構造出波端口模型,并進一步將波導與波端口分離構造出區(qū)域分解模型,將波導與波端口的互作用等效為兩個區(qū)域的外加激勵,從而使用迭代方法對此類問題進行求解.同時,并行計算技術的引入大大提高了矩量法求解電大尺寸問題的能力.數值仿真結果與實測結果的對比表明,波端口模型的使用可以有效地解決波導縫隙天線這一類電磁仿真難題.

矩量法;并行算法;波導縫隙天線;波端口

近年來,機載平臺的發(fā)展對機載天線的要求越來越高.大功率、高增益是現代工程應用中機載天線的普遍趨勢.目前,只能采用波導縫隙天線陣構建大功率天線.為了減少機載天線的設計、測試成本,前期的電磁仿真設計越來越顯得重要.然而,機載波導縫隙天線由于要求高增益,所以其電尺寸一般都比較大.常規(guī)的電磁仿真軟件(如HFSS,FEKO等)都難以在短期內計算出結果.Ansoft公司的HFSS軟件是基于有限元法的電磁仿真軟件,由于內存和計算時間的限制,Ka波段的波導縫隙陣通常無法仿真計算.FEKO是基于矩量法的電磁仿真軟件,其通過out-of-core[1]技術解決了內存不足的問題,但out-of-core將硬盤當內存使用的做法大大降低了計算速度,一個Ka波段波導縫隙陣的計算通常需要幾天時間.這迫使人們必須找到一種新的可實現的數值仿真方法.

筆者采用計算精度較高的矩量法作為數值仿真方法[2].通常矩量法分析波導縫隙天線存在3個難點:矩量法(Method of Moments,Mo M)是一種嚴格計算互耦的方法,與時域有限差分法(Finite Difference Time Domain,FDTD)和有限元法(Finite Element Method,FEM)等方法不同,矩量法中沒有理想吸收邊界的概念.這就使得矩量法中難以模擬出匹配負載,無法實現行波天線的計算.波導縫隙天線的縫隙形狀受到很大限制.傳統(tǒng)矩量法分析縫隙天線時,都是在縫隙開口處使用等效原理,即在開口面上放置等效磁流作為等效面內外耦合的中介[3].波導縫隙被等效為一個腔體,這就需要導出腔體格林函數.但是,當縫隙形狀不規(guī)則時,其格林函數很難找到矩量法的計算量非常大,而Ka波段的波導縫隙天線電尺寸通常也比較大,內存、CPU等計算資源束縛著矩量法的使用.對于第個問題(即波端口的建模),德國不萊梅大學的Bunger等[4]在2000年時給出解決方法.對于第個問題,筆者采用RWG基函數[5]將波導縫隙也剖分為電流面片,即在縫隙處不用等效原理,依然使用自由空間的格林函數進行全波仿真,避免了求解腔體格林函數.對于第個問題,筆者采用并行矩量法[6],在上海超級計算中心的“魔方”超級計算機上使用大量CPU核實現了核內(in-core)求解,大大地加快了計算速度.同時作為對Bunger等方法的改進,筆者提出的方法可將波導與波端口進行區(qū)域分解,從而可以采用基于區(qū)域分解的迭代法求解,使得可計算的問題規(guī)模進一步擴大.改進后的迭代法可以使波端口建模與波導上的基函數無關,易于實現.

1 矩量法中波端口的建模

由于矩量法中不存在理想吸收邊界,所以無反射的波端口的建模對波導饋電和行波天線的計算至關重要.波端口建模是基于孔徑耦合的等效原理[7]和模式匹配法[8-9].圖1給出了一個二端口波導的等效模型.

圖1 二端口波導等效模型

為了模擬波導無反射條件(即接匹配負載),可假設波端口外部接了一個半無限長波導.因為外部接了半無限長波導,則入射到波端口處的場將被導到無窮遠處而不會被反射回來.將原波導內區(qū)域記為區(qū)域Ⅰ,而假想的無限長波導區(qū)域記為區(qū)域Ⅱ.這樣假設以后,原問題變?yōu)榘霟o限長波導(區(qū)域Ⅱ)與原波導(區(qū)域Ⅰ)在波端口處的孔徑耦合問題.

根據孔徑耦合等效原理,首先假設波端口處被理想導體封閉,然后在理想導體面內側放置磁流M.因為波端口面是假想面,實際中并不存在,所以必須保證波端口內外兩側電磁場切向連續(xù).因而需要在其外側放置磁流-M,記波端口向內側的法向量為.波端口內外面上邊界條件為

由于波端口被理想導體封閉,則波端口內側面上還應該存在電流Jd.波導內壁上也應該存在電流,記為Jc.這樣以后,波導內問題就可以使用自由空間格林函數,而與波導形狀無關.對于區(qū)域Ⅱ問題,因為是半無限長波導,所以不能使用自由空間的格林函數,只能在波端口外側面上放置磁流-M,通過波導內的腔體格林函數求解.

1.1 波導內區(qū)域積分方程的建立

由圖1可以看出,波導內的電磁場由3個源產生:波端口上的電流Jd、磁流M及波導內壁上的電流Jc.其表達式為

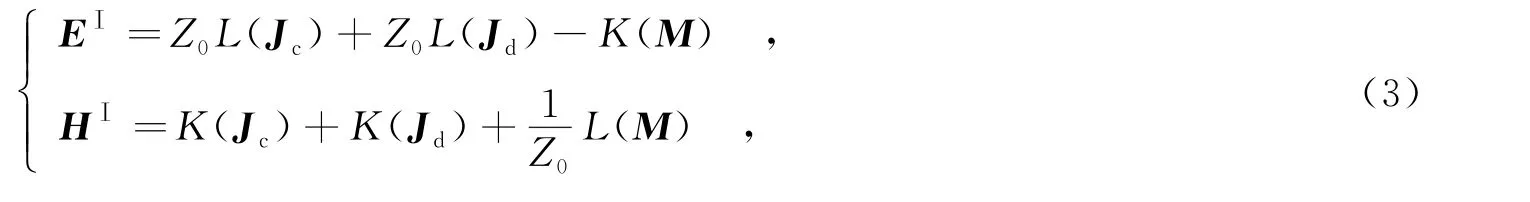
其中,Z0為波阻抗.L和K算子分別定義為

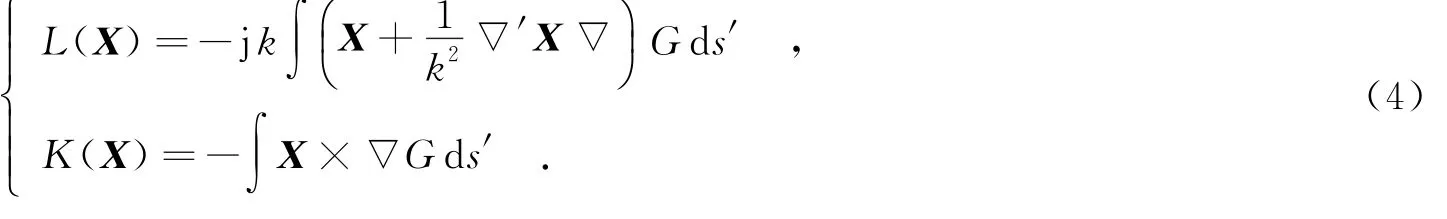
1.2 模式匹配法建立內外耦合積分方程

端口外側半無限長波導內的場由激勵(即入射波Ei,Hi)和波端口外表面上的磁流-M產生的(EⅡ, HⅡ)疊加而成.因為外側為半無限長波導,所以無法數值計算.此時可采用模式匹配法解析計算外側場.波導不同的模式即是波導格林函數的特征向量,模式匹配法也即等價于采用腔體格林函數計算半無限長波導內的場.因為波導的各特征模式已經天然地滿足了波導壁上的邊界條件,所以可以只在波端口面上放置激勵源-M,而不用考慮半無限長波導壁上的電流分布.

假設入射場為

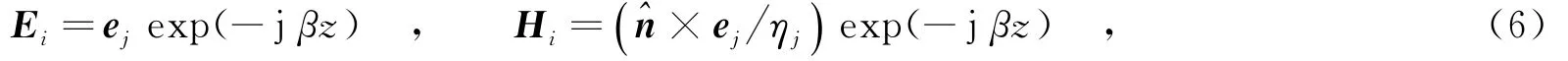
其中,ηj為第j個模式的波阻抗,ej為波導第j個模式的電場歸一化切向矢量.其歸一化方式為

式(7)的積分區(qū)間為整個波端口面.

首先,考慮到波端口被理想導體封閉,半無限長波導內電磁場(EⅡ,HⅡ)由入射波、全反射波和磁流產生的場疊加而成.磁流產生的場可由波導各模式組合而成,即

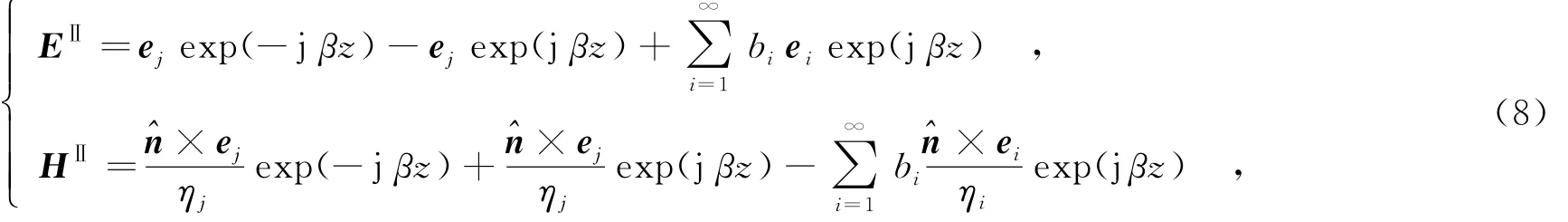
其中,bi為未知系數.因為在波端口面上z=0,所以,端口面外側電磁場可寫為

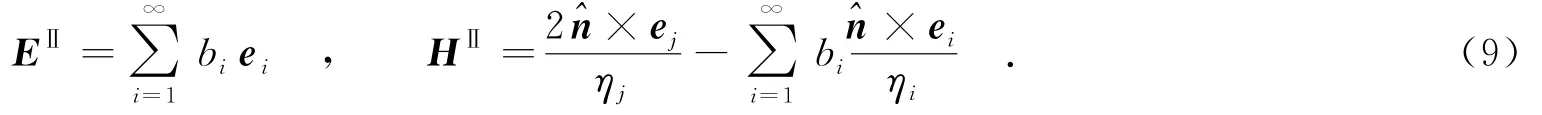
其次,考慮到波端口外側面邊界條件EⅡ×(-^n)=-M,所以由式(9)可得

由于式(7)波導各模式相互正交,所以將式(10)兩邊同乘以×ei,然后在波端口面上積分,則有

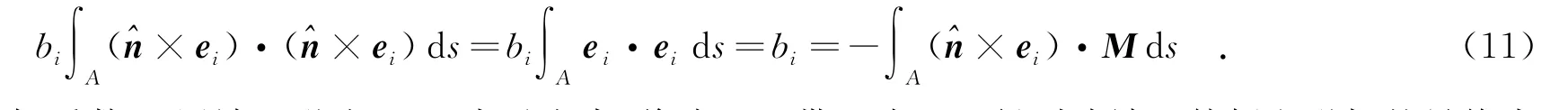
這樣就將未知系數bi用端口磁流-M表示出來.將式(11)帶入式(9),得到波端口外側電磁場的最終表達式為

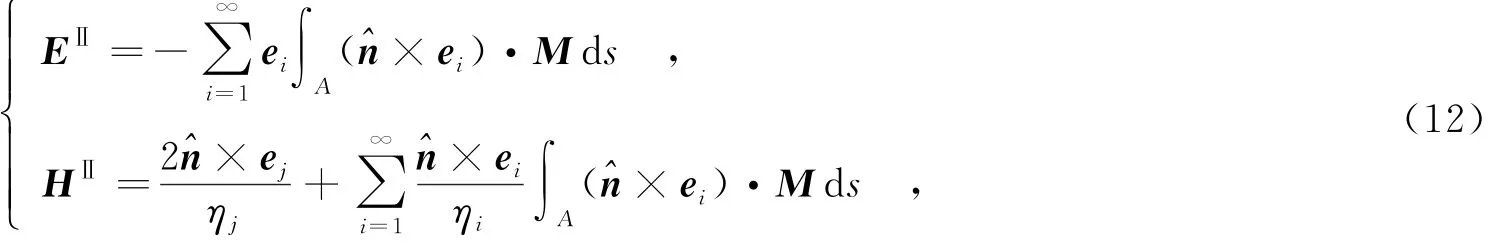
其中,ej表示以第j個模式激勵.

前面已經證明波端口內外兩側電場切向連續(xù),所以還須保證內外兩側磁場切向連續(xù),即HⅠ.因為內側面上邊界條件,所以.再由矢量旋轉關系,可得HⅡ互相垂直).代入式(12),得積分方程

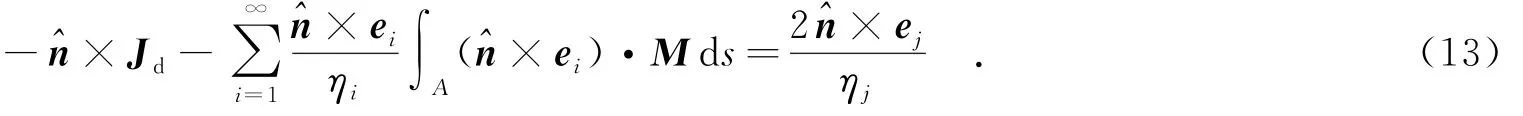
最后,整理得波導問題的積分方程組為

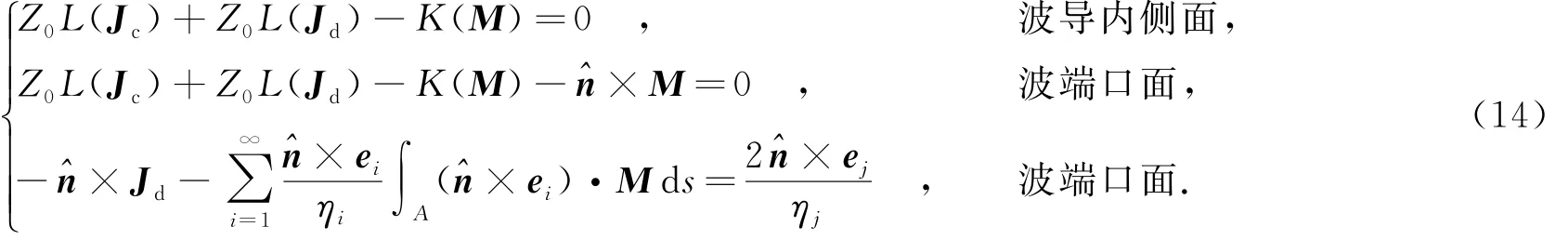
2 基于區(qū)域分解的迭代法求解

式(14)是適合直接求解的積分方程組.為了減少對原有矩量法程序的修改,下面提出一種基于區(qū)域分解思想的迭代解法[10],該方法可在邏輯上將波導壁與波端口看做分離的兩個區(qū)域.

針對單根天線,區(qū)域分解思想是將端口磁流對波導上電流的作用看成是區(qū)域Ⅰ的外加激勵.同時,將波導電流對端口磁流的作用也看做是區(qū)域Ⅱ的外加激勵.

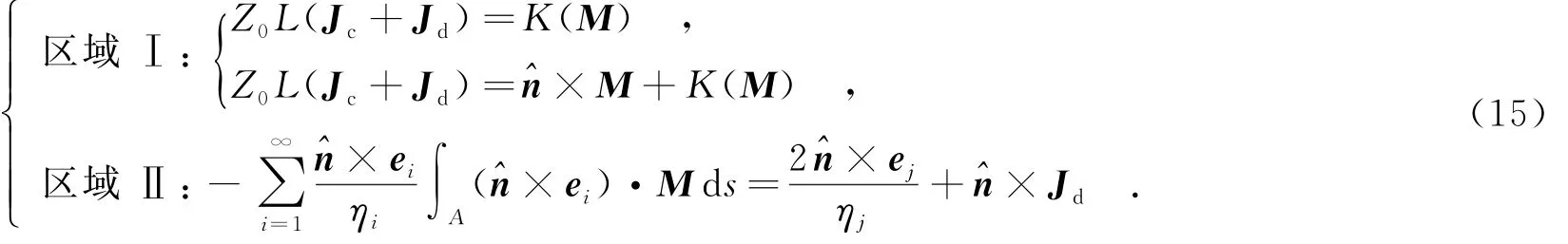
設置初始電磁流都為零,首先給區(qū)域Ⅱ一個激勵模式,解出端口磁流;然后將這個磁流作為區(qū)域Ⅰ的激勵算出電流分布;再用算出的電流更新區(qū)域Ⅱ的激勵.如此循環(huán)下去,直到電磁流的解穩(wěn)定.需要指出的是,通過數值實驗證明,這種迭代對于波導縫隙天線是收斂的.但對于單純的波導內問題(如濾波器),其收斂性難以保證.

此外,對于波導縫隙陣天線[11],由于不同天線單元之間通常都是物理上分離的,所以也可以進一步將各天線單元分解到不同區(qū)域,從而可以使天線陣問題通過先逐根分析每個單元,再逐根考慮各單元之間的耦合,最后迭代出結果.即使在相同內存下,可求解的問題規(guī)模也能夠進一步增大.因為天線單元物理上就是分離的,所以迭代收斂性較好.

3 數值算例

3.1 行波波導縫隙天線陣的計算

為了驗證筆者提出算法的正確性,此處計算了一個包含10個單元的X波段波導縫隙陣天線.其中每個單元為一個單側開有10個縫隙的行波天線.波導單元的尺寸為22.86 mm×10.16 mm×266.58 mm,天線工作頻率為9.375 GHz.各天線單元的饋電幅度與相位列于表1,天線陣的排布方式如圖2所示.

表1 各天線單元的饋電幅度與相位

由于頻率較高,天線的電尺寸較大,所以矩量法計算時剖分的網格較多.以1/10波長尺寸的三角形網格剖分時,共產生95 388個三角形面片.對應的矩陣方程有143 482個未知量,需要內存306.8 GB.如此規(guī)模的問題在一般PC機上串行計算顯然是不現實的.筆者在上海超級計算中心使用1 024個CPU核進行計算,填充矩陣耗時39 min,求解矩陣方程耗時30 min.該天線陣的歸一化遠場方向圖如圖3所示.

圖2 10單元行波陣天線模型

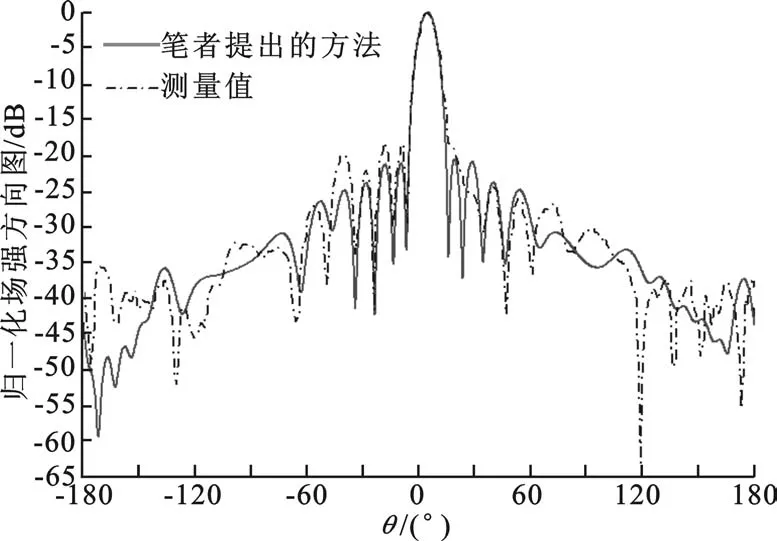
圖3 10單元波導縫隙天線陣遠場輻射方向圖

圖3中實線為筆者提出方法的數值計算結果,虛線為實際測量結果.可以看出,筆者提出方法的數值計算結果與實測結果吻合良好.尤其在主瓣區(qū)域,幾乎完全重合,從而證明了筆者構造的波端口模型在模擬計算行波天線時的有效性和準確性,為計算更大規(guī)模的波導縫隙天線陣提供了理論支持.3.2 Ka波段波導縫隙天線的分析

此處選取的計算模型為一根一側開有104個縫的二端口波導縫隙天線,如圖4所示.天線為一端口饋電,另一端口匹配的行波天線.在構造出波端口模型前,由于缺少理想匹配負載模型,矩量法難以模擬行波天線.以前的解決方法是在匹配端口上接高損耗的吸收媒質,將傳輸到匹配端口上的波損耗掉來模擬匹配.然而吸收媒質的吸收效果與頻率、波導尺寸、傳輸波的模式等因素都有關系,每一個天線要獨立設計吸收媒質的材料參數和所需要的媒質層數,該方法無法通用.即使設計出吸收媒質,它的吸收效果也難以達到100%.實踐證明,即使損耗媒質的吸收達到98%,依然會有少量的反射波回到波導內,對計算產生影響.

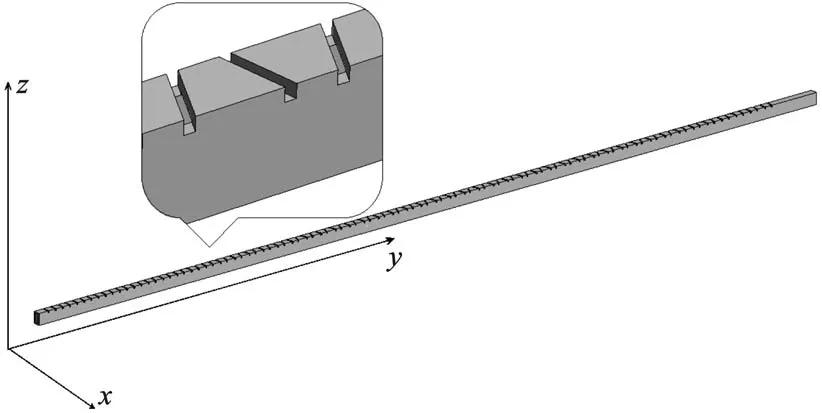
圖4 Ka波段波導縫隙天線模型

選取天線尺寸為7.112 mm×3.556 mm×591.6 mm,天線工作頻率為35 GHz.經矩量法剖分后產生132 474個未知量,需要261 GB內存.采用并行矩量法在“魔方”超級計算機中對該波導縫隙天線的輻射特性進行仿真計算,使用256 CPU核在2 h內即可得到計算結果.該天線的遠場方向圖如圖5所示.

圖5中實線為筆者采用波端口模型的計算結果,虛線為采用吸收媒質模擬匹配的計算結果.虛線的主瓣較窄,是因為方向圖采樣點的緣故.虛線為每1°采一個點,實線為每0.1°采一個點,所以虛線有跳過的點,導致顯示的主瓣較窄.在-45°、45°和105°附近出現的3個較大副瓣是交叉極化產生的.需要注意的是,在主瓣右側吸收媒質計算出的結果比波端口方法多出了一個小瓣.通過分析,筆者認為這是吸收媒質無法做到100%吸收而產生的反射波輻射.這也證明了波端口方法更加適合模擬匹配負載.

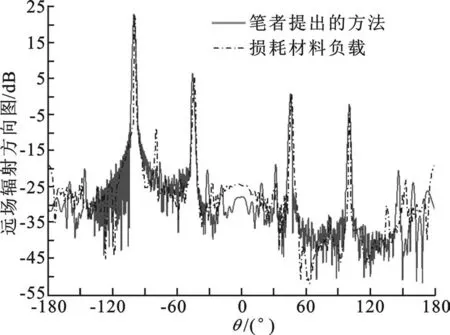
圖5 Ka波段波導縫隙天線輻射方向圖

4 結束語

在構造的波端口模型基礎上,筆者提出了適合于迭代求解的區(qū)域分解模型計算波導縫隙天線問題.由于波端口實現了匹配負載,使得行波天線的計算成為可能.并行計算和迭代方法的引入解決了大規(guī)模波導縫隙天線的計算難題,配合“魔方”平臺可以解決機載天線布局等工程中迫切需要解決的問題.筆者分析Ka波段波導縫隙天線只是解決工程問題的開始,下一步嘗試將天線加載到飛機平臺上去,解決更大規(guī)模的電磁仿真問題.

[1]Zhang Y,Sarkar T K.Parallel Solution of Integral Equation Based EM Problems in the Frequency Domain[M]. Hoboken:Wiley-IEEE Press,2009.

[2]Harrington R F.Field Computation by Moment Methods[M].New York:IEEE Press Series on Electromagnetic Wave Theory,1993.

[3]Lyon R W,Sangster A J.Efficient Moment Method Analysis of Radiating Slots in a Thick-walled Rectangular Waveguide[C]//IEE Proceedings H:Microwaves,Optics and Antennas,1981,128(4):197-205.

[4]Bunger R,Arndt F.Moment-method Analysis of Arbitrary 3-D Metallic N-port Waveguide Structures[J].IEEE Transactions on Microwave Theory and Techniques,2000,48(4):531-537.

[5]Rao S M,Wilton D,Glisson A W.Electromagnetic Scattering by Surfaces of Arbitrary Shape[J].IEEE Transactions on Antennas and Propagation,1982,30(3):409-418.

[6]Yan Y,Zhao W X,Zhao X W,et al.Parallel Computation of RCS of Electrically Large Platform with Coatings Modeled with NURBS Surfaces[J].International Journal of Antennas and Propagation,2012,2012:348052.

[7]Harrington R F,Mautz J R.A Generalized Network Formulation for Aperture Problems[J].IEEE Transactions on Antennas and Propagation,1976,24(6):870-873.

[8]Auda H,Harrington R F.A Moment Solution for Waveguide Junction Problems[J].IEEE Transactions on Microwave Theory and Techniques,1983,31(7):515-520.

[9]趙偉,趙永久,路宏敏.矩形波導不連續(xù)性的通用模式匹配法分析[J].西安電子科技大學學報,2008,35(5):894-898. Zhao Wei,Zhao Yongjiu,Lu Hongmin.General Analysis Method of Rectangular Waveguide Discontinuities by Mode Matching[J].Journal of Xidian University,2008,35(5):894-898.

[10]Peng Z,Wang X C,Lee J F.Integral Equation Based Domain Decomposition Method for Solving Electromagnetic Wave Scattering from Non-penetrable Objects[J].IEEE Transactions on Antennas and Propagation,2011,59(9):3328-3338.

[11]李建瀛,梁昌洪.波導窄邊縱縫的理論分析及頻掃縫陣[J].西安電子科技大學學報,1998,25(5):689-692. Li Jianying,Liang Changhong.Theoretical Analysis of the Longitudial Slot in the Narrow Wall of a Rectangular Waveguide and Frequence Scan Array[J].Journal of Xidian University,1998,25(5):689-692.

(編輯:郭 華)

Analysis of the radiation of slotted waveguide antennas using the parallel Mo M

WANG Yong,LIN Zhongchao,ZHANG Yu,LIANG Changhong
(Science and Technology on Antenna and Microwave Lab.,Xidian Univ.,Xi’an 710071,China)

This paper numerically analyzes the Ka band slotted waveguide antennas which are involved in engineering using parallel method of moments(Mo M).For lack of the match terminator,it is difficult for the Mo M to simulate the traveling wave antenna.To deal with this problem,the equivalent principle on the wave ports and the mode match methods are used to construct the model of wave ports.As an improvement,the waveguide and the wave ports are divided into different domains.The affections between the two domains are assumed as the external excitations of each domain.Then,the iteration method can be used to solve the equation.At the same time,the introduction of the parallel calculation technique can improve the ability of the Mo M to analyze the electrically large targets.The agreement of the measurement result and numerical result proves that the model of wave ports proposed in this paper can help to solve the problem of the simulation of slotted waveguide antenna validly.

method of moments(Mo M);parallel algorithm;slotted waveguide antenna;wave port

TN820

A

1001-2400(2015)05-0075-05

2014-05-20< class="emphasis_bold">網絡出版時間:

時間:2014-12-23

國家高技術研究發(fā)展計劃(863計劃)資助項目(2012AA01A308);國家自然科學基金資助項目(61301069,61072019);教育部新世紀優(yōu)秀人才支持計劃資助項目(NCET-13-0949);陜西省青年科技新星資助項目(2013KJXX-67);中央高校基本科研業(yè)務費重點資助項目(JY10000902002)

王 永(1987-),男,西安電子科技大學博士研究生,E-mail:yongmom@163.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20141223.0946.013.html

10.3969/j.issn.1001-2400.2015.05.013